Birinchi va ikkinchi tur egri chiziq integrallar (geometrik va fizik ma’nolari.) Grin formulasi

1. I tur egri chiziq integrali uni hisoblash va xossalari.

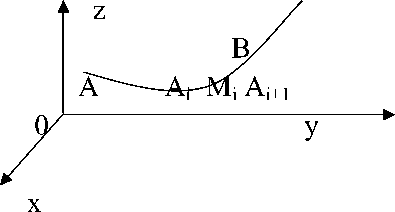
Tekislikda biror silliq AB egri chiziq berilgan bo’lib, unda f(x,y) funksiya aniqlangan bo’lsin.▲ yM

Ai Ai+1

A

0              x

Endi AB egri chiziqni    A=A 0 ,A 1 ,A 2 , ..., A n =B  nuqtalar bilan         A i A i+1

(i=0,...,n-1) yoylarga ajratamiz, har bir yoychada ixtiyoriy M i ( % i , n i ) nuqta olib bu nuqtadagi f(x,y) funksiyani qiymatini      f ( ^ i , n i ) deb belgilab quyidagi yig’indini tuzamiz.

n - 1

^a = Z f (&>n№ i    (1)

i = 0

max {A s i } = X deb belgilaylik.

Ta’rif: Agar AB egri chiziqda aniqlangan f(x,y) funksiya uchun tuzilgan (1) yig’indi k^0 da AB egri chiziqni Ai, Ai+1 yoylarga bo’lish usuliga va har bir Ai, Ai+1 yoychada Mi (^i,n i) nuqtani tanlab olish usuliga bog’liq bo’lmagan limitga ega bo’lsa , bu limitga f(x,y) funksiyadan AB egri chiziq bo’yicha olingan birinchi tip egri chiziqli integral deyiladi va lim a =

Л^ 0

n - 1

lim Z ^f ( Sn^ i = f f ^{( x} , y ) ^ds

■'                                  ( AB )

j f ( x , y ) ds deb belgilanadi. Demak.

( AB )

Birinchi tur egri chiziqli integralning asosiy xossalari:

• 1.   j f (x , y ) ds = j f ( x , y ) ds

• 2.     j Cf ( x , y ) ds = C j f ( x , y ) ds

• 3.      j [ f . ( x , y ) ± f 2 ( x , y ) ] ds = j f ( ( x , y ) ds ± j f 2 ( x , y ) ds

( АВ )                 ( BA )

( АВ )                   AB

• (k)                                             (k)(

• 4.    Agar k=k 1 +k₂ bo’lsa,   j ^{f ( x} , у ) ^ds = j ^{f ( x} , у ) ^ds + j ^{f ( x} , у ) ^ds bo’ladi.

(k )                       (k i)(

Agar birinchi tur egri chiziqli integralda f(x,y)=1 desak , u xolda j f (x,y)ds = j ds = S -egri chiziqning uzunligini beradi. Agar f(x,y) funksiyani musbat va (k)(k)

o’zgaruvchan chiziqli zichlik у = f ( x , y ) deb qarasak, j ^{f ( x} , ^y ) ^ds - integral k-egri

( k )

chiziqning massasini ifodalaydi.

Teorema. Agar f(x,y) funksiya, parametrik tenglamasi

X = ^ (t)

У = ^ 2 (t),

булган ( a <  t <  в )

(k) egri chiziqda aniqlangan va uzluksiz bo’lsa, u xolda

j ^{f ( x} , ^y ) ^ds  integral mavjud bo’lib

( k )

в                           I ----2--------------^------

J f(x,y)ds = j f [ ^ (t), ^ ,(t)\] ^ (t), +Щ ¹ (t)dt formula bilan hisoblanadi. (k)                 a

Agar fazodagi (k) egri chiziqning tenglamasi x = ^i (t),y = ^2 (t),z = ^3 (t)       (11 < t < 12) bo’lsa, t 2                                                ________________________________________________________ j f (x,y,z)ds = j f [^! (t),^2 (t),^3 (t)W^1 '2 (t) + ^2 '2 (t) + ^3 '2 (t)dt    bo’ladi.

( k )

t 1

Misol. Zichligi p = f ( x , y , z ) = Jyy qonun bilan o’zgaradigan va fazodagi parametrik

1, 2,       1    3

tenglamasi x = t , y = —t , t = -t

(0 < t < 1) lar bilan berilgan egri chiziqning massasini toping.

I___________________________________________________________ 1            _________________________________________ x + y + z dt = j t у/1 + t +1 dt =

. 2      1

t + д            1      ______________

-----² • 41 ⁴ + t ² + 1 + een ( t ² +  + V t ⁴ + t ² + 1)

2                  8        2

-11

• 1         1    3   3 + 2^3 ^

= — 3v3 - 1 + e-_en-------

• 8    ^           2      3 J

• 2.I kkinchi tur egri chiziqli integral.

Fazoda aniq yo’nalishli silliq (gladkoy) AB egri chiziq berilgan bo’lib, unda P(x,y,z), Q (x,y,z) va R (x,y,z) funksiyalar aniqlangan bo’lsin odatdagicha bu egri chiziqni A=A 0 , A 1 , ..., A n-1 ,  A n =B nuqtalar bilan A i A i+1 yoylarga ajratib har bir A i A i+1 yoychada ixtiyoriy M(

Z , n , Z ) nuqta olib quyidagicha yig’indi tuzamiz.

n - 1

£ [ ( Z , n , Z ) A x i + Q ( Z , n , Z ) A y , + R ( Z , U i , Z , ) A z ]     (2)

i = 0

A x i , A y i va A z i lar A i A_i+1 yoyning mos ravishda ox,oy, va oz o’qlariga bo’lgan proek s iyasi max {A x i } = X 1 ,max {A y i } = X 2 , max {A z i } = X ₃, deylik

Ta’rif. Agar AB da aniqlangan P (x,y,z), Q (x,y,z) va R (x,y,z) funksiyalar uchun tuzilgan (2) integral yig’indi ^ ^ 0, A2 ^ 0, A3 ^ 0 da AB egri chiziqni Ai Ai+1 yoylarga va har bir Ai Ai+1 yoyda ixtiyoriy M (£, n, Z) ,nuqtani tanlab olish usuliga botsliq bo ’ lmagan limitga ega bo’lsa bu limitga ‘ (x,y,z), Q (x,y,z) va R (x,y,z) funksiyalardan AB egri chiziq bo’ylab A dan V ga qarab olingan ikkinchi tip egri chiziqli integral deyiladi va j P (x, y, z) dx + j Q (x, y, z) dy + j R (x, y, z) dz  yoki

AB               AB               AB j P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz ko’rinishda yoziladi.

AB n -1

Demak j Pdx + Qdy + Rdz = lim У [ P A x _г + Q A y_t + R A z _г ]

AB                           1 2 ^0 i =1

z , 1   >0

Agar (2) integral yig’indini P,Q,R funksiyalarning ixtiyoriy bittasi yoki ixtiyoriy ikkitasi uchun tuzsak u xolda ikkinchi tip egri chiziqli integralimiz quyidagi ko’rinishlarda bo’ladi.

j Pdx + Qdy , j Qdy + Rdz , j Pdy + Rdz , j Pdy , j Qdy, j Rdz

AB

AB

AB

AB     AB     AB

-A-

Agar P(x,y,z), Q (x,y,z), R (x,y,z) funksiyalarni F kuchning ox, oy, oz o’qlaridagi proek ts iyasi sifatida qarasak va A x, A y, A z larni AB egri chiziqning F kuch tahsir qilayotgan nuqtasining ko’chishi A s ning ox, oy, oz o’qlaridagi proek s iyasi sifatida qarasak, ^

u xolda ikkinchi tur egri chiziqli integral F kuchning butun AB egri chiziq bo’ylab bajargan ishni beradi, ya’ni A= j ^Pdy + ^Qdy + ^Rdz bo’ladi.

AB

Ikkinchi tip egri chiziqli integralda integrallash yo’nalishini o’zgartirsak, integral qiymati o’z ishorasini o’zgartiradi jP(x,y,z)dx = -jР(x,y,z)dx chunki Ax1 ning ishorasi o’zgaradi.

AB

ВА

Ikkinchi tip egri chiziqli integralning qolgan hossalari esa birinchi tip egri chiziqli integralning xossalari kabi bo’ladi.

Teorema. AB egri chiziqning tenglamasi parametrik xolda berilgan bo’lib:

x = ^ 1 ( t г

У = ^ 2 ^{( t} )

= ^ 3 ( t )

a <  t <  в

(x,y,z) nuqta A dan B ga qarab harakat qilsin.

Agar ^ 1 ( t ) , ^ ₂ ( t ) , ^ ₃ ⁽ t ) , P(x,y,z),Q(x,y,z), R(x,y,z) funksiyalar AB da uzluksiz va uzluksiz $ ( t ) , ^ 2 ( t ) , ^ 1 ( t ) , hosilalarga ega bo ’Isa, u xolda j Pdx + Qdy + Rdz ikkinchi AB

в tur egri chiziqli integral mavjud va jP(x,y,z)dx = j[^(t),^2(t)^3(t)^1 (t)dt teng bo’ladi.

AB

a

Misol. Agar AB egri chiziqning parametrik tenglamasi x = Jcost y = a/ sin t

0 <  t <  -

2 J

2            2

> bo lsa, j x ydy ^- y ^xdx integralni hisoblang

АВ

Yechimi. dx =--sin t dt , dy = —cost- dt -bularni va x,y larni berilgan interalga 2 cos t              2 sin t qo’ysak.

j x ² ydy — y ² xdx = J

АВ

П

о V

— cos t     . I ----- sin t '

cos t ■ v sin t--.   + sin t • у cos t--

2V sin t                2v cos t у

dt =

П

1   2/     2 ,      -2             1   ²         П

— (cos t + sin t ) dt — dt — — .

2 0                       2 0       4

x — a cos t

Misol. Tenglamasi y — b sin t

* parametrik ko’rinishda berilgan ellipsning yuzi hisoblansin.

„   1               1 2

S —     xdy — ydx —     [ a cos t • b cos t + b sin t • a sin t J dt —

2 Z             2 0

ab

П

J (cos² t + sin² t ) dt — ab n

Adabiyotlar ro’yxati :

• 1.    Сlaudio Сanuto, Anita Tabacco “Mathematical Analysis”, Italy, Springer, I-part, 2008, II-part, 2010.

• 2.    W. WL.Chen “Linear algebra ”, London, Chapter 1-12, 1983, 2008.

• 3.    W.WL.Chen “Introduction to Fourier Series”, London, Chapter 1-8, 2004, 2013.

• 4.    W.WL.Chen “Fundamentales of Analysis”, London, Chapter 1-10, 1983, 2008.

• 5.    Soatov Yo U. Oliy matematika. Т., O’qituvhi, 1995. 1- 5 qismlar.

• 6.    Azlarov Т., Мansurov Х. Matematik analiz, - Тoishkent, O’qituvhi, 1-qism, 1989.

• 7.    Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Рады. Функции комплексного переменного. - Наука, 1997.

• 8.    V.Ye.Shneyder, А.I.Slutskiy, А.S.Shumov. Qisqaha oliy matematika kursi. Т., 1985., 2-qism.

• 9.    Беклемишев. Д.В. Курс аналитической геометрии и линейной алгебры. -М.: Наука, 1984.

• 10.    Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. М.: Наука, 1983.

• 11.    Piskunov N.S. Differensial va integral hisob. Oliy texnika o’quv yurtlari talabalari uсhun o’quv qo’llanma. Тoshkent, O’qituvсhi, 1974, 1, 2-qism.

"Экономика и социум" №2(93) 2022