Блокирующие стратегии в лабораторных кооперативных играх с наведенными заявками

Существует несколько подходов к изучению рыночных механизмов. Одним из наиболее популярных является теоретико-игровой подход. Другой подход связан с использованием методов экспериментальной экономики. Он позволяет с помощью создания лабораторных рынков моделировать различные экономические ситуации и анализировать поведение мотивированных участников экспериментов.

Потребности экспериментальной экономики порождают неисследованные ранее вопросы и задачи, которые относятся к области теории игр. Такие задачи необходимо решать при анализе результатов экспериментов.

Целью данной статьи является исследование аукциона, конструируемого по заданной кооперативной игре. Основной принцип построения аукциона, заключается в построении динамической игры, т.е. формальных правил взаимодействия игроков, позволяющих им объединяться в коалиции и реализовывать дележ выигрыша. Главное условие состоит в том, чтобы кооперативная игра, построенная по динамической игре, совпадала, с исходной кооперативной игрой.

Аукцион с закрытыми заявками можно считать наиболее простым для участников типом такого механизма. Участники такого аукциона, одновременно и независимо подают заявки на получение выигрыша. Затем диспетчер, максимизируя некоторый заданный функционал, объявляет участникам их выигрыши и множество реализовавшихся коалиций. Другой класс составляют открытые аукционы, в которых участники по некоторым правилам в режиме реального времени сами постепенно приходят к определенному компромиссному решению. Открытые аукционы порождают достаточно сложную динамическую игру.

Основная идея построения аукциона с наведенными заявками состоит в объединении положительных свойств указанных двух подходов. Этот аукцион подразумевает взаимодействие участников в реальном времени, но при этом сохраняет свойство простоты игры. Каждый игрок управляет всего одним (скалярным) параметром — величиной выигрыша, который он хочет получить, вступив в одну из коалиций. Каждому игроку в режиме реального времени предоставляется встречная заявка, согласившись с которой он вступит в наиболее выгодную на. данный момент коалицию. Таким образом, каждый игрок участвует в классическом открытом двойном аукционе с виртуальным оппонентом, заявки которого формирует диспетчер аукциона.

В разделе 2 приводится подробное описание механизма наведенных заявок для кооперативной игры трех лиц, отмечаются некоторые нюансы аукциона, выходящие за рамки классического открытого двойного аукциона. Выявляются так называемые блокирующие стратегии игроков, блокирующие состояния и множества достижимости.

В разделе 3 описываются эксперименты, проведенные в лаборатории экспериментальной экономики МФТИ и ВЦ РАН, приводятся и обсуждаются полученные результаты. Наиболее интересным результатом раздела 3 является сравнение двух серий экспериментов. На основе методов математической статистики делается заключение, что использование дополнительной информации о наличии блокирующих стратегий радикальным образом меняет поведение участников аукциона.

В разделе 4 дается описание аукциона с наведенными заявками для произвольной кооперативной игры на основе обобщения классического открытого двойного аукциона с помощью лексикографического правила. Введенный механизм с заданным лексикографическим правилом порождает множество блокирующих состояний, которое удается описать в явном виде. Это позволяет найти критерии их существования и установить связь с классическими результатами кооперативной теории игр, такими, как теорема Бондаревой—Шепли о непу-стоте ядра. Выделяется класс игр с нулевыми выигрышами малых коалиций, для которого оказываются справедливыми большинство выводов, сделанных для игры трех лиц.

2.    Кооперативная игра трех лиц

Рассмотрим кооперативную игру (с трансферабельной полезностью [1]) G = {N, V }, где N = {1,...,п} — множество игроков, V : 2^N ^ R — характеристическая функция, V = {V (S )}s_e2v, V(0) = 0. Будем предполагать, что характеристическая функция супераддитивна, что означает выполнение условий V (S ) + V (Т ) 6 V (S U Т ) VS,T С N : S ПТ = 0.

2.1.    Общие сведения об игре трех лиц

В этом разделе будем рассматривать игры, в которых множество игроков состоит из трех элементов N = {1, 2, 3}. Тогда множество коалиций будет состоять из семи элементов: три одиночных, три парных и одна коалиция трех игроков. Для уменьшения размерности игру трех лиц представляют в (О-І)-редуцированной форме [1]: выигрыши одиночных коалиций приводятся к нулевым, а также выполняется нормировка на выигрыш максимальной коалиции, чтобы он был равен единице (или сотне). Таким образом, остается три параметра — выигрыши парных коалиций: V(1) = V(2) = V(3) = 0, V(12) = а, V(13) = Ь, V (23) = с, V(123) = d = 100. В силу супераддитивности характеристической функции без ограничения общности можно положить 0 6 а 6 Ь 6 с 6 d = 100.

Одним из ключевых понятий в кооперативной теории является дележ. Дележ — исход игры, при котором реализуется максимальная коалиция и все игроки получают неотрицательные выигрыши. Пусть ж = (жі,ж2,жз) — это вектор выигрышей игроков, тогда множество дележей (см. рис. 1) можно записать так:

( Ж1 + Ж2 + жз = d, ( Xi >  0 Vi = 1, 2, 3.

Подмножество дележей, в которых каждая коалиция получает выигрыш, не меньший, чем она могла бы получить, отделившись от максимальной коалиции, называется ядром (см. рис. 2):

ж1 + ж₂ + жз = d,

< ж1 + ж₂ >  а, ж1 + жз >  Ь, ж₂ + жз >  с,

X i >  0 Vi = 1, 2, 3;

или

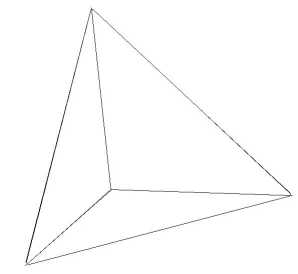
Рис. 1. Множество дележей

0 6 Жі 6 d —	с,
0 6 ж 2 6 d —	ь,
0 6 ж3 6 d —	а,
Ж1 + Ж2 + Ж3	= d.

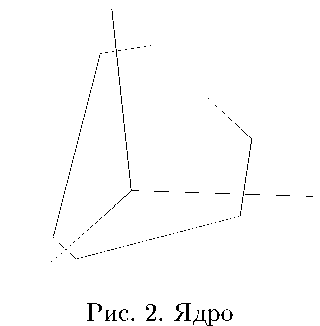
По теореме Бондаревой—Шепли [1] ядро не пусто тогда и только тогда, когда игра сбалансирована. Для приведенной кооперативной игры трех лиц сбалансированность игры определяется параметром к, где к = тіп(ко, к1, к2,кз), ко = d — ^+2+, к1 = d — с, к2 = d — b, кз = d — а.

Таким образом, ядро не пусто тогда и только тогда, когда к >  0. Причем если к >  0, то игра строго сбалансирована и ядро не вырождено, т.е. имеет максимальную размерность. Для игр трех лиц невырожденное ядро является плоским многоугольником.

2.2.    Динамическая игра для кооперативной игры

Обычно кооперативная игра, заданная характеристической функцией, строится по некоторой экономической или теоретико-игровой модели. Рассмотрим обратную задачу. Пусть задана кооперативная игра. Построим для нее некоторую динамическую игру, т.е. механизм взаимодействия игроков между собой. Согласно этому механизму игроки должны иметь возможность объединяться в коалиции и получать выигрыши по заданной характеристической функции. Естественное условие состоит в том, что кооперативная игра, соответствующая построенному механизму, должна совпадать с исходной кооперативной игрой.

Один из примеров построения подобных механизмов можно найти в [2], где для образования коалиции используется последовательное голосование за предложенный одним из игроков дележ.

Далее будет определен и проанализирован механизм наведенных заявок для кооперативных игр.

2.3.    Аукцион с наведенными заявками для игры двух лиц

Главная идея предлагаемого аукциона состоит в построении обобщенного непрерывного двойного аукциона [3,4]. Основной принцип непрерывного открытого двойного аукциона заключается в том, что два участника аукциона пытаются в непрерывном времени договориться о некотором соглашении, которое в простейшем случае представляет собой скалярную величину. При этом торги ограничены по времени, а итоговые выигрыши игроков зависят от резулвтата торгов. Если игроки не договорились, то выигрыш обоих игроков нулевой, а если они пришли к консенсусу, то получают ненулевые выигрыши, причем один из участников заинтересован в том, чтобы итоговая величина была как можно меньше, а второй — как можно больше. Аукцион является открытым, т.е. каждый из игроков делает прямое предложение другому и видит ответное предложение.

Наиболее простым примером служит аукцион «8В», в котором есть два участника 8 — продавец некоторого товара, а В — покупатель. Если сделка не произойдет, то каждый из игроков получит нулевой выигрыш, а если они договорятся о продаже товара по цене р, то продавец получит выигрыш ид = р — сд, а покуйатель — ив = ^в — Р, где сд и vb ~ затраты на производство товара для продавца и выкупная стоимость для покупателя соответственно.

Сам процесс торгов происходит следующим образом: игрок 8 заявляет цену рд (t) — спрос на товар, а игрок В — рв (t) — предложение, где t Е (0, Т) — время подачи заявки. Сделка будет заключена в том и только в том случае, если найдется такой момент времени to, для которого будет выполнено неравенство 5(to) d= р в (to) — р д (to) > 0, при этом цена сделки будет выбрана в пользу того игрока, изменение заявки которого привело к заключению сделки. Таким образом, цель обоих игроков — в течение процесса торгов так скорректировать свои заявки, чтобы спрос стал равен предложению.

Эту игру можно представить в виде кооперативной игры двух лиц: N = {1,2}, V (1) = V(2) = 0, V(12) = V = v b — сд. Тогда механизм дележа выглядит следующим образом. Каждый игрок делает заявку на получение некоторого выигрыша Рг(t); г = 1, 2; t Е (0, Т). При этом сделка будет заключена, только если найдется такой момент времени to. для которого будет выполнено условие ^(to) =f V — рі(^) — Р2(to) > 0. Для удобства игроков можно показывать им не прямые заявки оппонента, а наведенные: q t (t) = V — р j (t),г = j. Тогда условие заключения сделки (в данном случае образования коалиции) будет таковым: ^^(t) d=f V — q^(t) — Р г (t) >  0; г = 1,2; t Е (0, Т), причем 5 i (t) = 6(t) ^t^. Таким образом, можно считать, что каждый игрок формирует предложение «своего участия в коалиции», а диспетчер с помощью наведенных заявок создает спрос на «вступление в коалицию».

В общем случае в непрерывном двойном аукционе могут участвовать несколько продавцов и покупателей, при этом покупатели формируют на аукционе спрос, а продавцы — предложение.

2.4.    Аукцион с наведенными заявками для игры трех лиц

Теперь опишем механизм для случая произвольной строго сбалансированной кооперативной игры трех лиц в редуцированной форме. Есть четыре коалиции с ненулевыми выигрышами а, Ь, с, d. Как и в игре двух лиц, каждый игрок формирует заявку на получение некоторого выигрыша р^ (t); г = 1, 2, 3; t Е (0, Т ). Каждый игрок может вступить в одну из трех коалиций, соответственно он получает три наведенные заявки. Например, первый игрок получает заявки q“(t) = а — р₂(t), qi (t) = Ь — рз(t) и q^ (t) = d — р₂(t) — рз(t) — остатки от выигрышей коалиций после вычета заявок партнеров по соответствующим коалициям. В качестве заявки с предложением вступить в коалицию естественно выбрать максимальную из полученных заявок: qi(t) = max (q“(t),q^(t),q^(t)). Это согласуется с основным правилом непрерывного двойного аукциона, когда наилучшей заявкой типа «спрос» является заявка с максимальным номиналом.

Второе условие: если номиналы заявок равны, приоритет отдается той заявке, которая была подана раньше. В данном случае временем заявки будет максимальное время подачи простых заявок, из которых состоит наведенная. Но даже в при наличии всего трех игроков может возникнуть неоднозначность. Предположим, что сначала подал заявку игрок 1 в момент ti, затем игрок 2 в момент t2, тогда в момент t2 образуются сразу две заявки для игрока 3: q3.(t2) и q3 (t2). И если их номиналы окажутся равны, то заявки будут несравнимы в классическом аукционе. При возникновении описанной ситуации предпочтение отдается парным коалициям. Такой приоритет выбран для выполнения условий согласованности, о которых будет написано ниже.

Таким образом, каждый из игроков участвует в классическом непрерывном двойном аукционе с одним виртуальным партнером. Коалиция образуется тогда, когда один из игроков соглашается со встречной наведенной заявкой или подает свою заявку не больше, чем наведенная. В такой ситуации сумма заявок участников, по меньшей мере одной из коалиций, становится не больше, чем номинальный выигрыш этой коалиции. В случае, если в течение всей игры (0, Т ) не будет заключена ни одна сделка, все игроки получают нулевой выигрыш. При заключения парной коалиции оставшийся игрок получает нулевой выигрыш.

Условия согласованности выбираются из следующих соображений. Нетрудно проверить, что если ядро игры пусто, то никакие (в том числе совместные) действия игроков не смогут привести к образованию максимальной коалиции (для замыкающего игрока всегда найдется заявка от парной коалиции, которая будет для него выгоднее, чем максимальная). Значит, одним из необходимых условий возможности дележа является непу-стота ядра. Также можно заметить, что если ядро состоит из одной точки, например (100/3,100/3,100/3), когда а = b = с = 200/3, то в данном случае реализовать дележ тоже будет невозможно. Это следует из того, что если два игрока подадут свои заявки, то моментально образуется парная коалиция.

Определение. Подмножество дележей, которое может реализоваться в динамической игре, назовем множеством достижимости для аукциона с наведенными заявками.

Из вышенаписанного следует, что точки вне ядра не принадлежат множеству достижимости. Также можно проверить, что крайние точки ядра тоже не принадлежат множеству достижимости. Осталось проверить простые границы ядра (не угловые точки). Они не будут достижимы в том и только в том случае, если приоритет отдавать заявке, наведенной коалицией двух игроков.

Таким образом, для определенного выше механизма множество достижимости — это внутренние точки ядра. В случае, если бы мы определили приоритет в обратную сторону, множеством достижимости было бы множество всех точек ядра за исключением крайних точек. Такое множество не является ни открытым, ни замкнутым.

2.5.    Свойства аукциона с наведенными заявками

Построенный аукцион с наведенными заявками имеет ряд особенностей. Во-первых, нет гарантии, что исход игры будет дележом, т.е. может реализоваться любая парная коалиция, а также не реализоваться ни одна коалиции. Если образуется максимальная коалиция, то реализовавшийся дележ будет внутренней точкой ядра.

Во-вторых, в случае высоких выигрышей парных коалиций (маленькое ядро) возможен «эффект первой секунды»: все хотят побыстрее вступить в любую коалицию, чтобы получить хоть какой-то выигрыш, что, вероятно, приведет к образованию парных коалиций.

В-третьих, в случае маленьких выигрышей парных коалиций (большое ядро) может возникнуть «эффект последней секунды»: игра входит в некоторое равновесное состояние, когда парные коалиции заведомо невозможны, и все ждут окончания игры в надежде, что контрагенты смягчат свои заявки. Такое поведение, вполне вероятно, спровоцирует бескоалиционный (нулевой) исход.

2.6.    Блокирующие стратегии

Рассмотрим предложенный механизм более детально. Приведем анализ от лица первого игрока. Он не входит только в одну из четырех коалиций с номинальным выигрышем V (2, 3) = с. Зададимся вопросом, может ли игрок 1 сделать такую заявку, чтобы образование коалиции (2,3) стало невозможным в рамках аукциона. Запишем условие, при котором второму и третьему игрокам будет выгоднее вступить в максимальную коалицию: d — р₂ — р_і = q^ > q₃ = с — р₂, d — рз — р_і = q2 > q₂ = с — рз. Решая систему неравенств относительно р_і , полл-чаем р_і< d — с.

Проведя аналогичные рассуждения для остальных игроков, получим блокирующее состояние р = (рі, р2, рз):

0 < р_і< d — с,

0 < р₂< d — b, 0 < р₃< d — а, , рі + р2 + рз > d.

Назовем полученное множество большим предъядром (см. рис. 3). Связь с ядром можно заметить, сравнивая последнюю систему неравенств с (1). Можно сформулировать следующее утверждение. Если игра находится в состоянии р из большого предъядра, то никакой игрок своим ходом не сможет реализовать никакую коалицию с положительным выигрышем, кроме, быть может, максимальной.

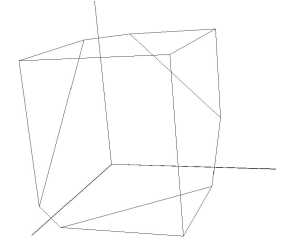
Рис. 3. Большое предъядро

Теперь построим множество состояний игры, в которых блокированными оказываются все коалиции, а не только выигрывающие:

р_і< d — с, р₂< d — b, р₃< d — а, рі + р2 <  d, рі + рз <  d, р₂ + рз <  d, d < рі + р2 + рз.

Назовем полученное множество малым предъядром (см. рис. 4). Сформулируем еще одно утверждение. Если игра находится в состоянии р из малого предъядра, то никакой игрок своим ходом не сможет реализовать никакую коалицию, кроме максимальной.

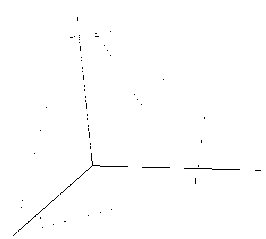
Рис. 4. Малое предъядро

3.    Постановка экспериментов

Для исследования свойств аукциона с наведенными заявками была поставлена серия экспериментов на искусственно созданном лабораторном рынке. Эксперименты проводились на базе лаборатории экспериментальной экономики МФТИ и ВЦ РАН в 2010 году. Участниками эксперимента были студенты 6 курса ФУПМ МФТИ.

Одной из главных трудностей проведения экспериментов является мотивирование участников. Наиболее распространенный способ мотивации участников — это выплата денежных вознаграждений в зависимости от достигнутых ими результатов. Существуют и другие способы стимулирования участников.

Анализируемые в данной работе серии экспериментов проводились в рамках учебного курса «Экспериментальная экономика». Мотивация участников обеспечивалась начислением учебных очков, которые влияли на зачетную оценку по данному курсу. В таких условиях отсутствие денежных вознаграждений чаще всего не снижает мотивацию участников.

В качестве лабораторных кооперативных игр трех лиц были взяты пять различных характеристических функций с различным размером ядра, оцениваемым параметром к (см. таблицу 1).

Таблица!

Примеры характеристических функций

	а	b	с	d	к
I	50	65	70	100	7.5
II	40	50	90	100	10
III	10	65	75	100	25
IV	10	25	45	100	55
V	10	20	30	100	70

3.1.    Описание экспериментов

Наиболее интересными для анализа представляются две серии экспериментов 19-11-2010 и 26-11-2010. Первую обозначим X, а вторую — У. В первой серии участвовало 12 человек, а во второй — 15, причем большая часть студентов участвовала в обоих экспериментах.

Игра состояла из последовательных раундов по 60 секунд (длительности начальных раундов были увеличены до 120-180 секунд для того, чтобы игроки привыкли к интерфейсу). При розыгрыше каждого раунда игры все участники эксперимента случайным образом разбивались на тройки, а внутри каждой тройки случайным образом распределялись роли. Характеристические функции менялись циклически каждые пять раундов, т.е. в раундах 1-5 была характеристическая функция I, в раундах 6-10 — II и т.д., всего 33 раунда. Таким образом, в первой серии было проведено 132 игры трех лиц, а во второй — 165.

Перед началом обеих серий экспериментов участникам были подробно описаны правила аукциона, алгоритмы смены раундов и способы распределения ролей внутри троек среди игроков в каждом раунде. Единственным отличием в информированности участников было то, что во втором случае им было рассказано о существовании в данной игре блокирующих стратегий.

3.2.    Анализ результатов

Распределения реализовавшихся коалиций приведены в таблице 2. Можно заметить, что для характеристической функции I (маленькое ядро) наблюдается 100%-я реализация коалиций. Также можно отметить, что в случаях IV и V (большое ядро) парные коалиции не образуются. Это согласуется с ожидаемой реализацией коалиций.

Т а б л и ц а 2

Результаты экспериментов. Реализованные коалиции

Серия	Набор	V (0)	V(1, 2) = а	V (1,3) = ь	V(2, 3) = с	V (1,2,3) = d	У
X	I	0	5	14	И	10	40
X	II	0	1	1	30	0	32
X	III	0	1	И	3	5	20
X	IV	1	0	0	0	19	20
X	V	1	0	0	0	19	20
	Всего						132
У	I	0	5	7	12	26	50
У	II	1	0	2	14	23	40
У	III	2	0	1	1	21	25
У	IV	3	0	0	0	22	25
У	V	2	0	0	0	23	25
	Всего						165

Для анализа эффектов первой и последней секунд разделим все раунды на три части по времени так, чтобы в каждый интервал попало примерно равное количество сделок. Получается, что начало раунда — это первые 15 секунд, а конец — последние 5. В таблице 3 приведены процентные соотношения игр, завершившихся образованием коалиций в начале раунда, а также игр, завершившихся в конце раунда (сюда же вошли игры, завершившиеся без образования коалиций). Эффектом первой (последней) секунды назовем такое распределение исходов, в котором доля игр, завершившихся в начале (конце) раунда, значительно превышает треть исходов. В серии X для игр с малым ядром (наборы I, II, III) ярко выражен эффект первой секунды, а в случае достаточно большого ядра (набор V) отмечается эффект последней секунды. В серии У эффекта первой секунды не наблюдается, а эффект последней секунды появляется и увеличивается с ростом ядра.

Т а б л и ц а 3

Результаты экспериментов. Эффекты первой и последней секунд

Серия	Набор	Игры, завершившиеся в начале раунда	Игры, завершившиеся в конце раунда
X	I	45%	5%
X	II	69%	0%
X	III	80%	5%
X	IV	30%	15%
X	V	20%	55%
У	I	20%	36%
У	II	25%	48%
У	III	24%	52%
У	IV	8%	76%
У	V	4%	84%

Поведение участников в проведенных лабораторных экспериментах в целом согласуется с предполагаемым поведением игроков на аукционе с наведенными заявками. Это говорит о том, что применяемый способ мотивирования игроков не снижает рациональности их поведения.

3.3.    Проверка статистических гипотез

Теперь проведем анализ влияния информированности участников на результаты экспериментов. Так как в рамках серии разбиение на тройки и распределение ролей внутри тройки было случайным, то последовательность получившихся коалиций можно считать независимыми реализациями некоторых дискретных случайных величин Х м в первой серии экспериментов и Ү м во второй серии (где М Е {I, II, III, IV, V }).

Для каждого М проверим гипотезу, что Х м и Х м являются реализациями одной случайной величины. Осуществлено к = 2 последовательных серии независимых наблюдений, состоящих из ni, ..., П к наблюдений соответственно, при этом в каждом опыте наблюдается некоторый переменный признак, принимающий одно из s различных значений (исходов).

S j = 1,..., к.

Пусть Vij — число реализатпш г-го исхода в j-й серии, так что   Vij = nj, i=1

одной и той же

Проверим гипотезу Но о том, что все наблюдения производились над случайной величиной. Воспользуемся критерием однородности у2 [5]. В качестве стати-

( s к    v 2

52 —-— г=1 j =i ^v * j ^v i *

— 1^ . Для распределения статистики T при n ^ то справедливо L(T|Но) ^ X2((s — 1)(к — 1)), и критическая область задается в виде Гщ = {t > ta}.

Полученные значения статистик и соответствующие значения р value приведены в таблице 4. Таким образом, при наиболее распространенном уровне значимости а = 95 гипотеза однородности отвергается для экспериментов с характеристическими функциями I, II и III. Мы можем сделать вывод, что дополнительная информация о наличии блокирующих стратегий радикальным образом повлияла на результаты экспериментов. Также можно сказать, что наличие блокирующих стратегий в данном механизме является нетривиальным фактом, требующим детального анализа аукциона.

Т а б л и ц а 4

Результаты экспериментов. Значения статистик и p-value

Набор парам.	Степени свободы ( s — 1)	Значение статистики	F-value (%)
I	3	8.481522	96.2959
II	4	30.64091	99.9996
III	4	21.89423	99.9790
IV	1	0.672256	58.7734
V	1	0.160714	31.1500

Для характеристических функций IV и V экспериментальные данные не противоречат гипотезе однородности. Этот факт является предсказуемым, т.к. в данных случаях парные коалиции слабы и практически любая стратегия будет блокирующей.

4.    Обобщение результатов

В этом разделе обобщим полученные результаты на случай произвольной кооперативной игры G = {N, V }, где N = {1,...,n} — множество игроков, V : 2 ⁿ ^ R — супералдитивпая характеристическая функция: V = {V(S)}^_с2 v. V (0) = 0. V (S ) + V (T) 6 V (S UT) VS,T GN :S nT = 0.

4.1.    Описание механизма

Для произвольной кооперативной игры можно построить следующий механизм наведенных заявок. Как и прежде, каждый игрок г формирует заявку на получение некоторого выигрыша Pi(t),i Е N,t Е (0, T). При этом он получает множество наведенных заявок:

q S (t) = V (S) — ^ p j (t),i EN,S C N, t Е (0, T ) -                  (2)

j^s\i остатки от выигрышей коалиций после вычета заявок партнеров по соответствующим коалициям. Как и в игре трех лиц, в качестве предложения вступить в одну из коалиций выбирается максимальная из заявок всех коалиций S, в которые входит игрок i qi(t) = max qS(t),i Е N, t Е (0, T).                               (3)

S : i E S

В непрерывных двойных аукционах в случае равенства сумм заявок обычно приоритет отдается заявке, которая была подана раньше. В нашем случае временем подачи заявки естественно считать максимальное время подачи простых заявок, из которых состоит наведенная. Но в таком случае не каждая пара заявок будет сравнима.

Наведенная игроку i Е N с коалиции S C N заявка q^S (t) состоит из |S| — 1 простых заявок, назовем их базой данной заявки. Временем подачи простой заявки p i (t) будем считать время последнего изменения этой заявки. Номинал q^S(t) заявки вычисляется по формуле (2), а вместо времени наведенной заявки будем оперировать с вектором времен простых заявок из базы, упорядоченным по убыванию: т(q i ) = (t(^),..., t(i)), где t j = т(p j )|j_Es ^— времена простых заявок игроков, входящих в коалицию S, удовлетворяющие условию t( ^ ) >  ••• >  t(i). Также будем предполагать, что времена подач простых заявок различны, т.е. игроки делают свои заявки строго последовательно. На практике при подаче нескольких заявок одновременно они обычно случайным образом упорядочиваются по времени, что приводит к удовлетворению указанного условия. Тогда в силу наших предположений любая пара заявок сравнима, причем сравнение производится с помощью лексикографического правила: сначала сравниваются номиналы заявок (чем больше, тем лучше), затем максимальные времена простых (чем меньше, тем лучше) и так далее. В рамках приведенного механизма может оказаться, что если база некоторой заявки является подмножеством другой, то более «короткая» будет лучшей (конечно, при условии равенства номиналов). Вот пример вложенной пары векторов времен: (3; 2; 1) и (3; 1). Тогда для полного соответствия надо в любой паре «вложенных» заявок «лучшей» считать «короткую», например (3; 2; 1) и (3; 2). Последнее условие эквивалентно приписыванию к вектору времен (справа) нулевого времени.

Таким образом, каждый из игроков участвует в классическом непрерывном двойном аукционе с одним виртуальным партнером. Коалиция образуется тогда, когда один из игроков соглашается с встречной наведенной заявкой или подает свою заявку не больше, чем наведенная. В момент описанного действия сумма заявок участников, по меньшей мере одной из коалиций, становится не больше, чем номинальный выигрыш этой коалиции. Результатом игры может быть любое непересекающееся множество коалиций, в том числе и пустое.

4.2.    Блокирующие состояния

Вектор, составленный из заявок всех игроков ж = { ж і } i _E N, будем называть состоянием игры. Суммы заявок игроков коалиций в состоянии ж обозначим следующим образом: ]Л Ж і = ж(S) VS C N. Блокирующими состояниями, как и в игре трех лиц, назовем боль- i E S шое и малое предъядро.

Определение. Малое предъядро для игры G = (N, V) — это множество в пространстве Rⁿ, удовлетворяющее условиям

' V(N) < ж(N),

< V(S) < ж(s)                      VS C N,                    (4)

ж(s) < V(N) — V(N\S) VS C N.

Неравенства второй строки (4) являются следствием остальных, поэтому определение малого предъядра можно записать так:

^J V(N ) <  x(N ),

[           x(S ) < V(N) - V(N \S) VS C N.

Определение. Большое предъядро для игры G = (N, V ) — это множество в пространстве Rⁿ, удовлетворяющее условиям

' V (N) < x(N ),

<   V (S ) <  x(S )

x(s ) < V (N ) - V (N\S)

VS C N,                         (5)

VS C N : V (N\S ) > 0.

Часть неравенств второй строки (4) являются следствием остальных, поэтому опреде ление большого предъядра можно записать так:

' V (N )  <  x(N),

<   V (S)  <  x(S )

x(S) < V (N ) - V (N\S)

VS C N : V(S) = 0,

VS C N : V ( n \S) > 0.

Для состояния

y(S ) ^d=^f p(S) - V (S )

игры p определим эксцесс для каждой коалиции:

VS C N, тогда по формулам (2, 3) разница между спросом и

def предложением для каждого игрока будет таковой: Oi = pi

- q_i = min a(S ) SvieS

Vi E N.

Теорема. Если игра находится в состоянии p из малого предъядра, то никакой игрок

своим ходом не сможет реализовать никакую коалицию, кроме коалиции всех игроков N.

Доказательство. Из неравенств первой и второй строк (4) следует, что в данный момент невозможна ни одна коалиция. Эксцесс для максимальной коалиции N равен o(N ) = p(N ) - V (N ). Перепишем последние неравенства из (4):

p(S) < V(N) - V(N\S) о о p(N) - p(N\S) < V(N) -V(N\S) о о p(N) - V(N) < p(N\S) - V(N\S) VS C N.

Значит, для любой собственной коалиции S выполнено a(S) > a(N). Поскольку каждый игрок i входит в максимальную коалицию, значит 6i = a(N), т.е. все дельты равны. Наведенная заявка для каждого игрока i будет вычисляться по формуле: qi = pi - ct(N) = V(N) - £ pj = qN > qS = pi - a(S) VS C N : i E S, т.е. для jeN\i любого игрока наведенная с максимальной коалиции заявка является строго максимальной среди всех наведенных этому игроку заявок. В силу механизма каждый игрок может реализовать только ту коалицию, которая дает наилучшую наведенную заявку для него.

Теорема доказана.

Теорема. Если игра находится в состоянии p из большого предъядра, то никакой игрок своим ходом не сможет реализовать никакую коалицию с положительным выигрышем, кроме, быть может, коалиции всех игроков N.

Доказательство. Проводя рассуждения, аналогичные рассуждениям в доказательстве предыдущей теоремы, получим, что a(S ) > a(N ) VS C N : V(S ) = 0. To есть для любого игрока наведенная с максимальной коалиции заявка будет строго больше (а значит, лучше) любой из всех заявок, наведенных этому игроку с коалиций с положительным выигрышем. Таким образом, у любого игрока наилучшая наведенная заявка наводится либо с максимальной коалиции, либо с нулевым выигрышем.

Теорема доказана.

Из этой теоремы следует следующая.

Теорема. Множество достижимости для механизма наведенных заявок - множество внутренних точек ядра.

Доказательство. То, что достижимы все внутренние точки ядра, следует из предыдущей теоремы, а замыкание двойного аукциона лексикографическим правилом делает недостижимым все границы ядра. Недостижимость же точек вне ядра следует из основного правила двойного аукциона: игрок, сделавший заявку последним (согласившись на встречную), получает максимально возможный выигрыш.

Далее сформулируем и докажем критерии существования предъядер.

4.3.    Критерии существования предъядер

Формулы, описывающие множества для предъядер, очень похожи на формулы определения ядра, поэтому критерии их существования будем искать схожими с условиями теоремы Бондаревой—Шепли.

Определение. Кооперативная игра называется строго сбалансированной, если для любого сбалансированного покрытия а : 2^N ^ [0; 1],   ^ a(S') = 1,Vi G N, выполнено

SCNviES условие ^ a(S)V(S) < V(N).

S C N

Теорема Для кооперативной игри п лии, следующие утверждения эквивалентны:

• 1)    игра строго сбалансирована;

• 2)    ядро игри имеет размерность п — 1;

• 3)    малое предъядра игры не пусто;

• 4)    большое предъядра не пусто.

Доказательство. Доказательство эквивалентности утверждений 1 и 2 аналогично доказательству теоремы Бондаревой—Шепли.

Если ядро имеет размерность п — 1, тогда существует вектор x, принадлежащий множеству внутренних точек ядра:

( V(N ) = x(N ),

t            x(S ) < V (N ) — V (N\S) VS C N.

Обозначим е = min ^V (N ) —V (N\S)—x(S )) > 0. тогда д.тя вектора z = (x1 + “, x₂, ..., x_n^ получим z(N ) > V(N ) и z(S ) <  V(N ) — V(N\S) VS C N, т.е. точка z будет принадлежать малому предъядру. Из непустоты малого ядра следует непустота большого, т.к. по определениям малое содержится в большом. Осталось доказать, что из непустоты большого предъядра следует непустота множества внутренних точек ядра (6).

Пусть большое предъядро не пусто, тогда существует x, удовлетворяющий системе нера

V (N )   ,              .

V ( n ) _{+ E} (xi,x2, ...,x_n)

венств (5). Обозначим е = x(N ) — V(N ) >  0. Для вектора z V (N )

вектора z положительны:

что для вектора z выпол

получим: z(N ) =        _|_ x(N ) = V(N ). Все компоненты

z(S) > 0 VS C N. т.к. x(S) >  V(S) >  0 VS C N. Докажем.

нены нижние неравенства из (6): z(S) < x(S) < V(N ) — V (N\S)  VS C N : V (N\S) >  0;

z(S) = z(N ) — z(N\S ) = V (N ) — z(N\S) <  V (N ) = V (N ) — V (N\S) VS C N : V (N \ s ) = 0.

Таким образом, z является внутренней точкой ядра.

Теорема доказана.

4.4.    Игры с нулевыми выигрышами малых коалиций

Легко убедиться, что в случае, если все коалиции имеют положительный выигрыш, большое и малое предъядра совпадают. Поэтому для разделения введенных понятий понятий необходимо рассмотреть подмножество игр, в которых часть коалиций имеют нулевой выигрыш.

В данном разделе будет выделен класс игр, в котором болвшое и малое предъядра качественно отличаются, причем для болвшого предъядра можно привести наглядную геометрическую и экономическую интерпретацию.

Определение. Игра с нулевыми выигрышами малых коалиций — кооперативная игра, характеристическая функция которой удовлетворяет условиям:

Г V(S ) = 0 VS С N : |S| 6 п — 2, t V (S) > 0 VS С N : | s | = п - 1.

Нетрудно убедиться, что приведенная игра трех лиц принадлежит этому классу. Многие результаты, полученные для игр трех лиц, будут справедливы и для всего класса игра с нулевыми выигрышами малых коалиций.

Обозначим выигрыши ненулевых коалиций и сумму выигрышей всех коалиций следующим образом:

V-j = V (N\i) Vi E N,

Vn d=f V (N), ^-N d= £ V—j jeN и будем считать, что 0 < V-n 6 ... 6 V-i 6 Vn.

По теореме Бондаревой—Шепли игра с нулевыми выигрышами малых коалиций строго сбалансирована тогда и только тогда, когда к = тт(ко,к) > 0, где к0 = VN--—, ieN                             п — 1

K j = V n — V- i Vi E N.

Геометрическую интерпретацию можно сформулировать в следующем виде. Для строго сбалансированных игр с нулевыми выигрышами малых коалиций большое предъядро является усеченным параллелепипедом:

Vn <  £ Xj, ieN

*   0    <    x_j                    Vi E N,

X j   <  V n — V-j Vi E N.

Экономическая интерпретация заключается в наличии индивидуальных блокирующих стратегий в механизме наведенных заявок для строго сбалансированных игр. Каждый игрок i может поста вить заявку 0 <  p j <  V n — V-j, которая будет блокировать все коалиции с ненулевым выигрышем, не содержащие игрока i, т.е. поставив такую заявку, игрок получает гарантию того, что если образуется коалиция, то она обязательно будет содержать его, причем этот игрок получит выигрыш щ = pj.

Но, как и для игр трех лиц, такая блокирующая заявка не дает гарантии, что игрок получит заявленный выигрыш, т.е. может так оказаться, что в интервале времени (0,Т) не будет заключена ни одна коалиция.