Blur Classification Using Wavelet Transform and Feed Forward Neural Network

Published Online April 2014 in MECS DOI: 10.5815/ijmecs.2014.04.03

Barcode is the leading technology for automatic identification, which is used in a extensive range of realtime applications with a variety of codes [1]. In Comparison to 1-D barcode, 2-D barcode has high density, capacity, and reliability. Therefore, 2-D barcodes have been progressively more adopted these days. For example, a consumer can retrieve crucial information from the web page of the magazine or book, when he reads it, by just capturing the image of the printed QR code (2-D barcode) [2] related to URL. In addition to the URLs, 2-D barcodes can also symbolize visual tags in the supplemented real-world environment [3], and the adaptation from the individual profiles to 2D barcodes is usually exists [4]. Whereas, 1-D barcodes are traditionally scanned with laser scanners, 2-D barcode symbologies need imaging device for scanning.

Detecting bar codes from images taken by common used handheld devices like mobile camera is particularly challenging due to geometric distortion, noise, and blurring in image at the time of image acquisition. Image blurring is often an issue that affects the performance of a bar code identification system. Two most common types of blur are motion and defocus blur. Motion blur appears due to the relative motion among image capturing device and object at the time of image acquisition. Defocus blur appears due to the inaccurate focal length adjustment. Blurring induces the degradation of image quality. There are two approaches of deblurring; one is blind and other non-blind deconvolution. For blind restoration of barcode images it is essential to estimate blur parameters for deblurring. However, before application of any blur parameters estimation approach automatic blur classification is extremely desirable (i.e. to determine what type of blur is available in the acquired image).

Tong et al. [5] presented a method that applies Haar wavelet transform to estimate sharpness factor of the image to decide whether the image is sharp or blurred and then in case blurred image, they measure strength of blur. Yang et al. [6] addressed the motion blur detection scheme using support vector machine to classify the digital image as blurred or sharp. Aizenberg et al. [7] presented a work that identifies blur type, estimates blur parameters and perform image restoration using neural network. They considered four kinds of blur namely rectangular, motion, defocus, and Gaussian as a pattern classification problem. Bolan et al. [8] proposed an image blurred region detection and classification method which can automatically detect blurred image regions and blur type identification without image deblurring and kernel estimation. They developed a new blur metric using singular value feature to detect the blurred regions of an image and also analyze the alpha channel information and classify the blur type of the blurred image regions into defocus blur or motion blur, respectively. Renting et al. [9] presented a framework for partial blur detection and classification i.e. whether some portion of image is blurred as well as what types of blur arise in motion and defocus categories. They consider maximum saturation of color, gradient histogram span and spectrum details as blur features. Chakrabarti et al. [10] presented a method, which combines local frequency components, local gradient variations, and color channel information under the MRF segmentation framework to detect and extract motion blurred region in the image. Yan et al. [11] made an attempt to find a general feature extractor for common blur kernels with various parameters, which is closer to realistic application scenarios and applied deep belief networks for discriminative learning. Tiwari et al. [12] used statistical features of blur patterns in frequency domain and identified blur type with the use of feed forward neural network.

Wavelet features have been extensively used in object and texture classification. However, we have not found any application of wavelet features for blur classification. In this paper, we have proposed the use of wavelet features extraction of blur patterns in frequency spectrum and feed forward neural network for blur classification.

This paper is organized into seven sections including the present section. In section two to four, we discuss the theory of image degradation model, wavelet transform and feed forward neural network in that order. Section five describes the methodology of blur classification scheme. Section six discusses simulation results and in the final section seven, conclusion is discussed.

• II.    Image degradation model

The image degradation process in spatial domain can be modeled by the following convolution process [12]

( , )= ( , )∗ℎ( , )+ ( , ) (1)

where ( , ) is the degraded image, ( , ) is the uncorrupted original image, ℎ( , ) is the point spread function that caused the degradation and ( , ) is the additive noise. Since, convolution in spatial domain is equivalent to the multiplication in frequency domain, equation (1) can be written as

( , )= ( , ) ( , )+ ( , ) (2)

When the scene to be recorded translates relative to the camera at a constant velocity (vrelative) under an angle of θ radians with the horizontal axis during the exposure interval [0, texposure], the distortion is motion blur. Defining the length of motion as L = v × t , the point spread function (PSF) for uniform motion blur described as [12]

ℎ ( , )= {    √

+   ≤      =-tan

otherwise

The frequency response of PSF is called optical transfer function (OTF). The frequency response of h , is a SINC function given by

( , )=     (π ( cos + sin ))     (4)

Fig. 1(a) and (b) show an example of motion blur PSF and corresponding OTF with specified parameters.

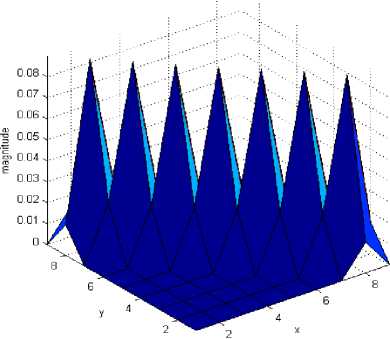
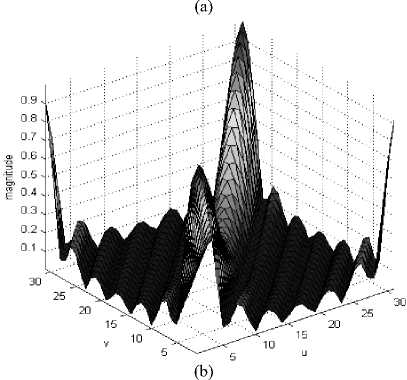
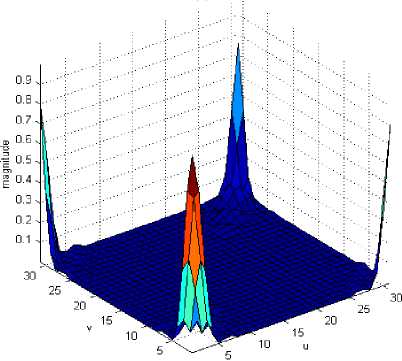
Fig1. (a) PSF of motion blur with angle 450 and length 10 pixels, (b) OTF of PSF in (a)

The out of focus blur caused by a system with circular aperture can be modeled as a uniform disk with radius R as [12]

ℎ ( , )= {

if ^+? <^R ₍₅₎

otherwise

The frequency response of equation (5) is given by (6), which is based on a Bessel function of the first kind [12]

( , )=

( √     )

√

where / is the Bessel function of first kind and R is radius of uniform disk. Fig.2 (a) and (b) show an example of PSF and corresponding OTF of defocus blur with specified radius.

The image degradation model for the presence of defocus and motion blur simultaneously in the image is given as [12]

9(x,y) = f(x,y) * h^y) * hm(x,y) + л(x,y) (7)

Since convolution is commutative, so joint blur PSF can be obtained as convolution of two blur functions as

h⁽x,y) = h^x^) * h_m⁽x,y)         (8)

where h( (x, y) and h_m(x,y) are point spread functions for motion defocus and blur respectively and ' * ' is the convolution operator.

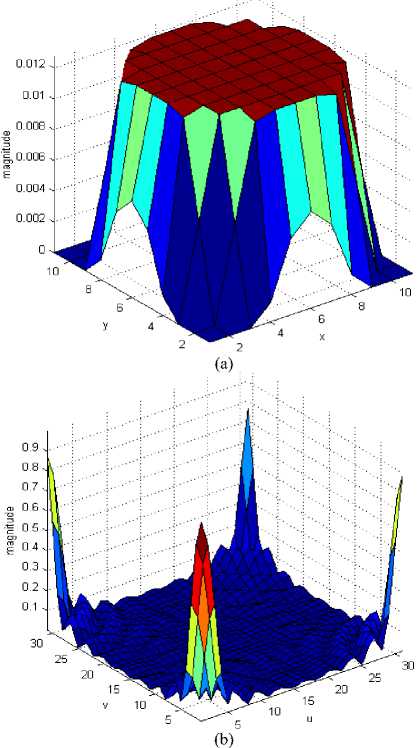
Fig2. (a) PSF of defocus blur with radius 5 pixels, (b) OTF of PSF in (a)

Fig.3(a) and (b) show an example of PSF and corresponding OTF of joint blur with specified parameters. This paper treats the blur effect caused by defocus and camera motion and combination of these two. This work does not consider additive noise in image degradation.

• III.    Wavelet transform

The wavelet transform [14, 15] is a dominant and impressionable framework for image processing and analysis tasks. It is broadly used in the fields of image compression, segmentation, de-noising, recognition and fusion etc. The wavelet transform is based on the use of elementary functions, known as wavelets and scaling, which are produced by scaling and translation of a base function, called mother wavelet defined as

0 °, ^b (x) ₌ A0p_» )             (9)

where ‘a’ is the scaling term and ‘b’ is the translation factor. In 2-D, it can be represented as

0 °, b (x,y) = —= 0^,^)

EaTa2   ° а.г a2 /

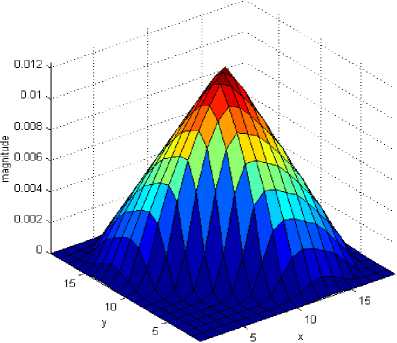
(a)

(b)

Fig3. (a) PSF of joint blur with angle 450 and length 10 pixels, radius 5 pixels, (b) OTF of PSF in (a)

The wavelet transform of an image f(x,y) is a set of coefficients cц that depend on the scale and shifting of the signal defined as

Ctj = EL f ⁽x, y)0 °"^{b (}x, У) dx Уу        (11)

As a result of this, the wavelet transform decomposes the original image into a series of sub images with different levels. The two-dimensional discrete wavelet transform (DWT) hierarchically decompose an input image into a sequence of successively lower resolution images and their associated approximate and detail coefficient images. DWT is implemented by a set of filters, which are convolved with the image rows and columns. An image is convolved with low-pass and high-pass filters and the odd samples of the filtered outputs are discarded, resulting in down sampling of the image by a factor of 2. The l level wavelet decomposition of an image I(x, y) results in an approximation image Xl and three detail images Hl, Vl, and Dl in horizontal, vertical, and diagonal directions respectively. The features derived from these wavelet-transformed images are shown to be valuable for texture analysis [16]. Hiremath et al. [17] have discussed various significant characteristics of the wavelet transform based approaches for texture classification: (a) It is efficient to remove correlation available in the data and accomplish the similar objective as the linear transformation, (b) It gives direction sensitive information which is crucial in texture analysis, and (c) The computational complexity is appreciably reduced due to the wavelet decomposition.

We have considered blur patterns in frequency domain as textures and used this information to categorize the blur.

• IV.    Feed forward neural network

An Artificial Neural Network (ANN) [12, 18] is a system, which is used to carry out classifications on datasets. The ANN can access a solution space that is not possible with the usual logical inferences based computational systems. in addition to this, it can operate on non-linear classification problems. they are composed of interconnected processing units called neurons that work as a collective unit. It can be used to establish complex relationships among inputs and outputs by identifying patterns in data. The feed forward neural network refers to the neural network which contains a set of source nodes which forms the input layer, one or more than one hidden layers, and single output layer. In case of feed forward neural network input signals propagate in one direction only, from input to output. There is no feedback path i.e. the output of one layer does not influence same layer. One of the best and widely recognized learning algorithms in training of multilayer feed forward neural networks is Back-Propagation. The back propagation is a supervised learning algorithm, that receives sample of the inputs and related outputs to train the network, and then the error (difference between real and expected results) is calculated. The idea of the back propagation algorithm is to minimize this error, until the neural network learns the training data.

• V.    Methodology

Blurring reduces sharp features of image such as boundaries, shape, regions, objects etc., which creates problem for further image analysis tasks. In spatial domain, it is not easy to differentiate the motion blur and defocus blur. However, these blurs have different appearance in frequency spectrum, which makes possible to categorize blurs. If we transform the blurred image in frequency spectrum, it can be seen from frequency spectrum of motion blurred image that the dominant parallel lines appear, that are orthogonal to the motion orientation with near zero values [19, 20]. In defocused blur, we can see presence of some circular zero crossing patterns [21, 22] and in case of coexistence of both blurs joint effect becomes visible. Fig.4 shows the effect of different blurs on the Fourier spectrum of original image. We propose the use of these frequency patterns as texture features for blur classification. The steps of the algorithm blur classification are given in fig.6. These are six major steps: image acquisition, preprocessing of images, computation of logarithmic frequency spectrum, feature extraction of blur patterns, data normalization, designing of neural network classifier system. In the initial steps we preprocessed image. Then, we have found the logarithmic frequency spectrum of blurred and non blurred image to get the blur patterns. Once the blur patterns acquired, the method demands the extraction of features. So the wavelet features have been calculated in the next step to prepare the training and testing database. Finally with this feature database training and testing performed using feed forward back propagation neural network.

(c)

(d)

(e)                                         (f)

Figure 4: (a) Original image containing QR code [34] (b) Motion blurred image (c) Fourier spectrum of original image (d) Fourier spectrum of blurred image with motion length 15 pixels and motion orientation 900 (e) Fourier spectrum of blurred image with defocus blur of radius 10 (f) Fourier spectrum of image with coexistence of both blurs

After that step, the windowed image can be transferred into the frequency domain by performing a fast Fourier transform. The power spectrum is calculated to facilitate the identification of particular features of the Fourier spectrum. However, as the coefficients of the Fourier spectrum decrease rapidly from its centre to the borders, it is difficult to identify local differences. Taking the logarithm of the power spectrum helps to balance this fast drop off. In order to obtain a centered version of the spectrum, its quadrants have to be swapped diagonally. In view of the fact that the remarkable features are around the centre of the spectrum, a centered portion of size 128 X 128 is cropped to perform wavelet transform, which reduces computation time. Images in fig. 5(a) to 5(d) show the results of hann windowing.

• A.    Preprocessing

Blurred image requires a number of preprocessing steps before feature extraction. First, the color image obtained by the digital camera is converted into an 8-bit grayscale image. This can be made by averaging the color channels or by weighting the RGB-parts according to the luminance perception of the human eye. The periodic transitions from one boundary of image to the next frequently lead to high frequencies, which are converted into visible vertical and horizontal lines in the power spectrum of image. Because these lines may distract from or even superpose the stripes caused by the blur, they have to be removed by applying a windowing function previous to frequency transformation. The Hanning window gives a fine trade-off between forming a smooth transition towards the image borders and maintaining enough image information in power spectrum. A 2-D Hann window of size N X M defined as the product of two 1D Hann windows:

w[n,m] = ;(1 + cos[2?r^]) (1 + cos[2^])   (12)

(d)

(c)

Figure 5: (a)-(d) Hann windowed images of images shown in figures 4(a), 4(d), 4(e) and 4(f) respectively.

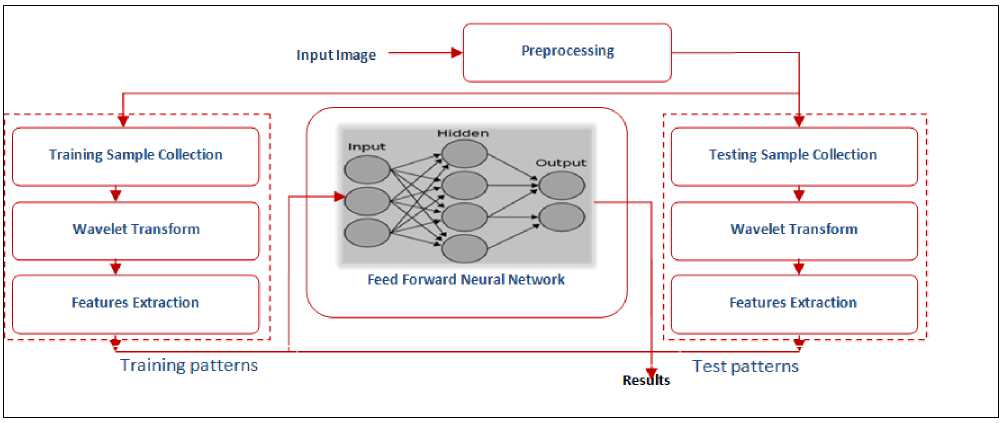
Figure 6: Blur classification framework

• B.    Feature Extraction

Matlab Wavelet transforms toolbox used for wavelet transform with decomposition level 3. The Haar wavelet is chosen for its superior discriminating power. In comparison to other wavelets, the Haar wavelet is theoretically straightforward and precisely reversible without edge effects. The Haar transform does not have overlapping windows, which reflects only changes between adjacent pairs of pixels. These features make them ideal for the use in the wavelet transform. The wavelet energy gives the distribution of energy along the frequency axis over the scale and orientation of a detail image. Since most of the relevant texture information has been impartial by iteratively low-pass filtering, the energy of an approximation image is generally not considered as a feature. After achieving the wavelet transform the mean and standard deviation of the coefficients related with each decoposition is calculated. The mean of a detail image I is calculated as:

where M x N is the size of detail image and E_t is the energy of detail image. Energy is calculated by the sum of absolute values of wavelet coefficients.

= ∑    ∑ |I (x, y)|(14)

The standard deviation of a detail image is calculated as:

√∑     ∑     (|  ( , )|)

4i/1

All these features are arranged in a manner such that the standard deviations remain in the first half of the feature vector and the means are arranged into the second half of the feature vector. So, we obtain a feature vector of size 18 consists of 9 mean energies and 9 standard deviations f = (f ,f …,f ) for each image. We have used this feature vector f to categorize blurs.

• VI.    Simulation results

  The image database used for the simulation is the Brno Institute of Technology QR code image database [23]. 350 images from the database were considered. Then, the three different classes of blur i.e. motion, defocus and joint blur were synthetically introduced with different parameters to make the databases of 1050 blurred images (i.e., 350 images for each class of blur). A three layer Neural network was created with 18nodes in the first (input) layer corresponding to size of input feature vector, 1 to 50 nodes in the hidden layer, and 3 nodes in the output layer (i.e. one node for each class). We have varied the number of nodes in the hidden layer in a simulation in order to determine the optimal number of hidden nodes. This was to avoid over fitting or under

fitting the data. Finally, ten nodes in the hidden layer were selected to run the final simulation. The whole training and testing features set is normalized into the range of [0, 1], whereas the output class is assigned to zero for the lowest probability and one for the highest. During designing of neural network a cross-validation method is used to improve generalization ability. To perform the cross-validation procedure whole feature set is divided randomly into 3 sets training set, validation set and test set with a ratio 0.5, 0.2 and 0.3 respectively. The training set is used to learn the network. The validation set is used to validate the network i.e. to regulate network design parameters. The test set is used to test the generalization ability of the designed neural network.

The aim of any classification technique is maximizing the number of correct classification given by True Positive Rate (TPR) and True Negative Rate (TNR), whereas minimizing the wrong classification given by False Positive Rate (FPR) and False Negative Rate. Terms True Positive (TP), True Negative (TN), False Positive (FP) and False Negative (FN) can be defined as below.

• (i) . True Positive (T_P): if test pattern is positive and it is predicted as positive, it is considered as a true positive.

• (ii) . True Negative (TN): if test pattern is negative and it is predicted as negative, it is considered as a true negative.

• (iii) . False Positive (FP): if test pattern is negative and it is predicted as positive, it is considered as a false positive.

• (iv) . False Negative (FN): if test pattern is positive and it is predicted as negative, it is considered as a false negative.

In blur classification problem, we have used the four metrics for result evaluation as given in equations (16)(19).

Number of true positive (T )

TPR =

Totalnumber of positive in dataset (Np )

Number of true negative (T )

TNR =--------------------------N (17)

Totalnumberof negative in dataset (N )

Number of false positive (F )

FPR =-----------------------------P (18)

Totalnumberof negative in dataset (N )

Number of false negative (F )

FNR =---------------------------N (19)

Totalnumberof positive in dataset (N )

The values of positive and Negative samples used as testing samples are 350 and 700, respectively for each blur categories. The data in Table 1 gives the above discussed rates given by the classifier. Classification accuracy for each blur class is calculated as mean of true positive rate and true negative rate. Testing results give classifications accuracies as 99.3%, 99.7%, and 100% for motion, defocus and joint blur categories respectively. These classification accuracies show the high precision of our method.

Table 1: Blur Classification results

	Classification Results(in percentage)
Blur Type	True Positive Rate	True Negative Rate	False Positive Rate	False Negative Rate
Motion Blur	98.6	100	0	1.4
Defocus Blur	100	99.3	0.7	0
Joint Blur	100	100	0	0
Motion blur classification accuracy 99.3
Defocus blur classification accuracy 99.7
Joint blur classification accuracy 100

• VII.    Conclusion

In this paper, we have proposed a new blur classification scheme for barcode images taken by digital cameras. The blur type identification scheme utilizes the wavelet transform to discriminate blur patterns appear in frequency domain of blurred image, while considering them as texture features. This work classifies blur in motion, defocus and joint blur categories, which can further help to choose the appropriate blur parameter estimation approach for non-blind restoration of barcode images. In future this work can be extended by considering the noise in image degradation model.

ACKNOWLEDGMENT