Боковая поверхность зуба цилиндрических зубчатых колес

соединяющей эвольвентную поверхность с поверхностью впадин.

Боковая поверхность прямого зуба представляет собой цилиндрическую эвольвентную поверхность. Для косого зуба боковая поверхность является винтовой эвольвентной поверхностью. В общем случае эту поверхность можно рассматривать в двух параметрических направлениях. Первое направление представляет собой перемещение по эвольвентному профилю зуба в его торцевом сечении. Второе направление определяется прямолинейным перемещением эвольвенты вдоль оси зубчатого колеса для прямозубых колес и винтовым перемещением – для косозубых колес. В координатной форме векторная функция эвольвенты записывается в следующем виде [3]:

Rb sin ф

rэ

Rb С^ф +

- R b ф cos ф R _b ф sin ф

где R b – радиус основной окружности зубчатого колеса; φ – угол развернутости эвольвенты (рис. 1). Точка M 1 на боковой поверхности прямого зуба описывается вектором

r = r + r

э см

где r cм – вектор смещения по оси OZ .

В координатной форме вектор r запишется:

	" R b	sin ф		"- R b	ф cos ф		■ 0 "
r =	Rb	cos ф	+	Rb	ф sin ф	+	0
		0      _		V	0       _		_- Vt _	,        (3)

где V – скорость перемещения конца вектора r вдоль оси OZ ; t – время перемещения.

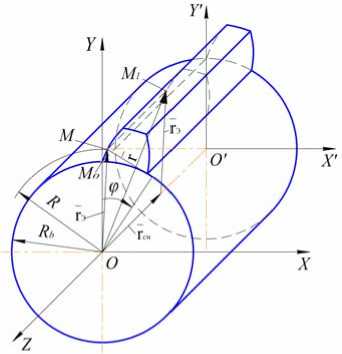
Рис. 1. Боковая поверхность прямого зуба

Зубья косозубого колеса в торцевом сечении имеют эвольвентный профиль. При этом на любом радиусе колеса совокупность точек, принадлежащих боковой поверхности зуба, в направлении его оси, образует винтовую линию. Другими словами, каждая точка эвольвенты при движении вдоль оси косозубого колеса совершает винтовое движение (рис. 2).

Винтовая линия на основном цилиндре зубчатого колеса радиуса R b определяется формулой

Rb sin T1

r = R b cos О

— a ф1

где φ 1 – угол поворота проекции вектора r на плоскость XOY ; a – параметр, характеризующий движение по винтовой линии вдоль оси колеса OZ .

Текущий параметрический угол φ 1 изменяется от своего нулевого значения, до значения φ 1 max , которое он принимает на тыльном торцевом сечении (рис. 2). Величина φ_{1 max} зависит от значений угла наклона β b линии зуба к оси колеса и ширины зубчатого венца b . В выражении ( 4 ) максимальное значение координаты вектора r по оси OZ в принятой системе равняется по модулю ширине зубчатого венца

I— a ф, I = b г 1max

Длина дуги M′0M′′0 (рис. 2) равняется, с одной стороны b tg βb , а с другой – Rb φ1max , то есть можно записать:

М0М0' = btgpb = Rb т .     (6)

Из формулы (6) находится максимальное значение угла поворота φ 1 :

b

T1 max = — Wb Rb

.

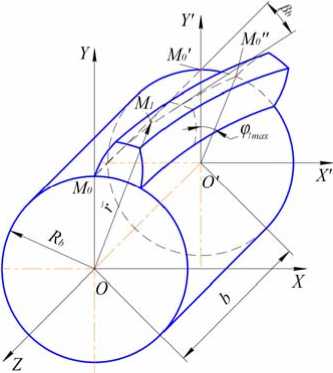
Рис. 2. Боковая поверхность косого зуба

С учетом выражения (7) параметр a определяется соотношением b = V = Rb срл co teB, т 1 max g b где ω – угловая скорость вращения проекции вектора r на плоскость XOY вокруг оси OZ.

Положение любой точки на эвольвентном профиле прямого зуба колеса определяется значением угла развернутости эвольвенты φ (рис. 1). Радиус R изменяется от значения радиуса R b основного цилиндра до значения радиуса R a цилиндра вершин зубьев колеса. Радиус R определяется как модуль векторной функции эвольвенты (1) и записывается выражением

R = R b 4v+T

Соответственно текущее значение угла φ определяется по формуле т =

f pA ²

( R ; 1

— 1

Для косого зуба необходимо дополни- тельно учитывать, что каждая точка его эволь-вентного профиля все время поворачивается в плоскости XOY относительно оси OZ на величину текущего угла φ1. Поэтому после вычисления координат точки эвольвенты в любом ее положении необходимо найденный вектор повернуть на угол φ1 путем умножения его на матрицу поворота [M]. В результате в общем виде векторная функция винтовой эвольвентной поверхности косого зуба колеса запишется:

r = [ M ] ^{( Г}э ^{+ Г}см )

Или в координатной форме

	cos ф 1	sin ф 1	0 "
r =	- sin Ф 1	COS ф 1	0
	. 0	0	1 _

(	" R b sin ф"		- R b ф cos ф		_ 0 "	^
	R b cos ф	. +	R b ф sin ф	+	0
V	_ 0      _		_         0       .		" «ф 1 .	7

С учетом преобразований выражения (12) векторная функция боковой эвольвентной поверхности зуба косозубого колеса окончательно опишется формулой

Rb (sin (ф + Ф1)- ф cos(ф + Ф1))

r = - Rb (cos(ф + Ф1) + фsin (ф + Ф1))

- а ф 1

В результате вектор r , восстановленный в точку M 1 винтовой эвольвентной поверхности (рис. 2), имеет относительно вектора эвольвенты два аффинных преобразования: поступательное перемещение вдоль оси зубчатого колеса и поворот относительно этой оси.

Выводы: запись эвольвентной поверхности зубчатых колес в координатной форме позволяет любые пространственные преобразования. Используя пространственное описание поверхностей зубчатых колес, можно моделировать сложные многопараметрические и многофункциональные процессы зубообработки, а также различные эксплуатационные и технологические процессы. Например, возможен расчет пятна контакта при взаимодействии сопряженных зубьев колес. Кроме этого, рассмотрение зубьев колес в пространственном отображении дает возможность определить их бочкообраз-ность, а также погрешности, возникающие при зубообработке.