Большие прогибы, потеря устойчивости и закритическое поведение пологих панелей и арок переменной толщины на упругом основании

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2024PNRPU MECHANICS BULLETIN

Задаче о закритическом поведении элементов конструкций, начиная с проблем устойчивости и анализа больших прогибов стержня при сжатии, решенных Л. Эйлером (см., например, в [1]), посвящалось большое количество работ, в том числе и задачам о больших прогибах стержней в упругой среде (см. например, [2–12]). Задача о больших прогибах пологих цилиндрических бесконечно длинных панелей была впервые исследована в работе [7]. После этого появился ряд публикаций, в которых эта задача исследовалась при других геометрических формах панелей, других условиях нагружения, а также в случае панелей, образованных из пластин предварительным сжатием. Был обнаружен эффект, который не наблюдался в [7], а именно было выявлено [8], что при некотором значении сосредоточенной силы при симметричной деформации возможно бесконечное число форм равновесия. В частности, для предварительно изогнутой пластины это достигается после прохождения нагрузкой ее максимальной величины и уменьшения её до нулевого значения.

Для задач о потере устойчивости конструкций на упругом основании было выявлено, что, в отличие от решения Эйлера, при определенных геометрических параметрах стержня после потери устойчивости для дальнейшей деформации стержня в упругой среде требуется уже меньшая сила, чем критическая [9; 10]. Фактически происходит хлопок, как это имеет место в большинстве случаев при поперечном нагружении арок или предварительно искривленных стержней.

В [11] представлено аналитическое исследование нелинейно упругого поведения после выпучивания пологих круглых арок, имеющих неодинаковые упругие вращательные торцевые ограничения. Для вывода дифференциальных уравнений равновесия используется принцип стационарности потенциальной энергии. Установлено, что арка с упругими концевыми заделками не может выгибаться в бифуркационном режиме.

В [12] представлено аналитическое исследование процесса обрушения шарнирно закрепленной неоднородной пологой круглой арки под действием равномерного радиального давления. Достоверность аналитического результата проверяется путем сравнения с результатами МКЭ.

В развитие [7, 8] в работах [13; 14] рассмотрены арки, изготовленные из линейно-упругого функционально-градиентного материала и подверженные воздействию сосредоточенной радиальной или вертикальной мертвой силы. Для описания поведения используются те же гипотезы, что и в [7; 8], а дифференциальные уравнения задачи выводятся из принципа виртуальной работы.

Вариационной постановке задачи устойчивости геометрически нелинейного деформирования тонкостенных конструкций посвящено немало работ. При этом обычно в задачах нелинейного деформирования стержней используется вариационное уравнение в виде принципа возможных перемещений, как это отмечается в [15] (см. также [10; 1–17]). В ней на примере плоской задачи показывается, что с использованием энергетически сопряженных векторов усилий и деформаций вариационную задачу можно сформулировать в виде задачи поиска точки стационарности функционала типа Лагранжа. При этом появляется возможность двумя способами получить уравнения устойчивости: как уравнения в вариациях для исходной дифференциальной постановки, а также как уравнения Эйлера для второй вариации функционала Лагранжа. Рассмотрена плоская круговая двухшарнирная арка, нагруженная потенциальной «мертвой» нагрузкой, для статических задач получены точные нелинейные дифференциальные уравнения задачи. Доказана эквивалентность дифференциальной и вариационной постановок. Получены точные уравнения устойчивости, учитывающие геометрически нелинейное деформирование в докритическом состоянии.

Задачам о больших прогибах, а также закритиче-ском поведении арок и в последние годы уделяется немало внимания. Например, в [16] рассматривается плоская круговая двухшарнирная арка, нагруженная потенциальной «мертвой» нагрузкой. Для описания напряженно-деформированного состояния и устойчивости равновесия используется геометрически точная теория, в соответствии с которой каждая точка стержня имеет две трансляционные степени свободы и одну вращательную, не зависящую от трансляционных. Для получения решения не используются никакие упрощения о величинах перемещений и углов поворота, а также учитываются все жесткости стержня – продольная, сдвиговая и изгибная. Получены точные нелинейные дифференциальные уравнения статической задачи. Сформулирована вариационная постановка в виде задачи поиска точки стационарности функционала типа Лагранжа. Доказана эквивалентность дифференциальной и вариационной постановок. Получены точные уравнения устойчивости, учитывающие геометрически нелинейное деформирование в докритическом состоянии. На основе полученных уравнений решена задача устойчивости равновесия круговой арки при действии «мертвого» радиального давления с учетом всех жесткостей стержня. Получено характеристическое трансцендентное уравнение, а также асимптотическое решение этого уравнения в виде простых формул, пригодных для практического применения. Выполнено сравнение полученного решения, учитывающего все жесткости стержня, с классическим решением, учитывающим только изгибную жесткость.

Немало работ, посвященных практически важным задачам. Например, в [17] проводится расчет на устойчивость криволинейных стержневых элементов сплошно-стенчатых стальных арок по изгибно-крутильной форме, в [18] проводится анализ большепролетных арок (крыш велодромов) при разных условиях закрепления, в [19] исследуется устойчивость многослойных цилиндрических прямоугольных в плане панелей, выполненных из поперечно-клееной древесины. Продолжаются и теоретические исследования (например, в [20] выводятся непротиворечивые уравнения теории плоских криволинейных стержней при конечных перемещениях, а в [21] исследуются вопросы разрешимости уравнений в геометрически нелинейных краевых задачах для пологих оболочек по теории типа Тимошенко).

Рассматриваются и нестандартные условия закрепления, например, в [22; 23] исследуется нелинейное поведение и устойчивость пологих арок с упругими горизонтальными и вертикальными опорами. Аналогичное исследование в [24] сопровождается сравнением с экспериментальными результатами. В [25] также учитывается упругая податливость опор и представлено аналитическое исследование потери устойчивости многослойной арки. При этом обнаружено, что арка может терять устойчивость либо в режиме предельной точки, либо в режиме бифуркации (как это было отмечено ранее и в работе [8]), а ее поведение очень чувствительно к жесткости опоры. Проведено сравнение с результатами, полученными методом конечных элементов. Этому же направлению посвящена работа [26], в которой неустойчивость в плоскости пологой арки исследуется в зависимости от перемещений и поворотов опор. В [27] исследуется влияние формы сечения на потерю устойчивости как в плоскости, так и из плоскости арки. Аналогичное исследование, но численным методом, проведено в [28]. В [29; 30] аналитически решаются задачи с учетом нелинейно упругой податливости опор повороту оси. В [31] приведены экспериментальные и аналитические результаты, но уже с учетом упругопластических, а в [32] – аналитические решения с учетом вязкоупругих деформаций.

Ниже также рассматривается пологая панель или арка (рис. 1), которая может иметь упругое основание, упругие опоры, совокупность различных нагрузок. В этом случае использование уравнений равновесия приводит к трудностям, поскольку нелегко найти их точные решения на каждом участке и сшивать их. В таких случаях целесообразнее использовать вариационные методы. Они удобны и в оптимизационных задачах, поэтому задачи разработки простых методов их решения остаются актуальными.

1.    Постановка задачи и метод её решения

Рассмотрим пологую панель длины L (см. рис. 1), которая может иметь переменную цилиндрическую жесткость, упругие опоры и упругое основание, которое также может иметь переменный коэффициент постели. При цилиндрическом изгибе панели задача становится одномерной и совпадает с точностью до обозначений с задачей об арке, а отличие заключается лишь в том, что вместо цилиндрической жесткости D = Eh ³ /12(1 -ν ² ) необходимо использовать изгибную жесткость EJ , а в качестве жесткости на растяжение K = Eh /(1 -ν ² ) необходимо использовать ЕА , давление на поверхность панели надо заменить распределенной по линии нагрузкой q .

В рассматриваемой задаче использование уравнения равновесия элемента панели приводит к трудностям, поскольку в общем случае найти его точное решение на каждом участке (как это делалось в [7; 8] при простых видах нагружения и простых формах панели) не представляется возможным. Трудности увеличиваются и в том случае, когда нагрузка представляет собой совокупность, например, сосредоточенных сил, кусочно-переменных распределенных нагрузок, поскольку приходится сшивать решения, полученные на участках с однородными нагрузками. В таких случаях предпочтительнее использовать энергетический метод решения задач, который будет изложен ниже.

В качестве примера рассмотрим панель, загруженную так, как это показано на рис.1. Принимаем, что материал упругий. Тогда в случае пологой панели можно принять закон Гука в виде:

M ( x ) = D ( x ) ⋅ w ( x ) ", (1)

здесь M ( x ) – погонный изгибающий момент, D ( x ) – цилиндрическая жесткость, w ( x ) – прогиб, штрихами обозначены производные по координате x .

Закон Гука для N представим в виде:

N =- K ( x ) ⋅ε ( x ), (2)

здесь K ( x ) – жесткость на сжатие или растяжение.

Считаем, что панель лежит на упругом основании, а его реакция r ( x ) связана с прогибом w законом Винклера:

r ( x ) = - k ( x ) ⋅ w ( x ), (3)

здесь k ( x )– коэффициент постели. Упругая опора на расстоянии x 3 (см. рис. 1) имеет жесткость с и связана с прогибом w соотношением

R =- c ⋅ w ( x ₃ ). (4)

Как и в работах [7; 8], можно считать, что погонная продольная сила N постоянна по длине (т.е. не зависит от x ).

^у A

f ( x )

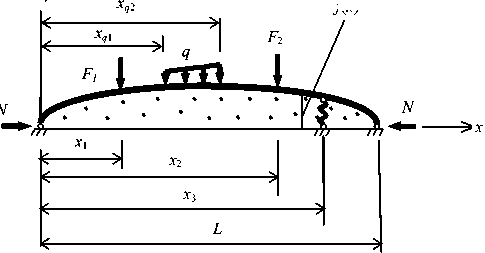
Рис. 1. Схема нагружения панели или арки

Fig. 1. Loading diagram of the panel or arch

Разрешающее энергетическое соотношение запишем в виде:

LL

∫ D ( x ) ⋅ w " ⋅δ w " ⋅ dx - N ∫ ( f + w ) ′⋅δ w ′⋅ dx +

L

+ ∫ k ( x ) ⋅ w ⋅δ w ⋅ dx + ∑ F_i ⋅δ w ( x_i ) +          (5)

0i xq2

+ ∫ q(x)⋅δw⋅dx+R⋅δw(x3)= 0, здесь δw – виртуальный прогиб, первое и второе слагаемые – работы изгибающих моментов и продольной силы, третье слагаемое – работа реактивной силы r упругого основания, два последних слагаемых – работы внешних сил, четвертое – работа реактивной силы R.

Для решения задачи об определении функции w ( x )

можно ее представить в виде ряда по некоторым функциям, удовлетворяющим условиям закрепления на опорах:

n w=∑Aiϕi(x).                  (6)

i = 1

В качестве δ w_i примем эти же функции:

δ w_i =ϕ _i ( x ).

После подстановки (6) в (5), задав разные δ w_i , получим линейную систему уравнений для коэффициентов A_i , которые будут представлять собой функции неизвестного пока усилия N .

Для того чтобы связать N и прогиб w , рассмотрим соотношение для ε, записанное с учетом немалых прогибов в виде:

ε= u ' - ^w + ¹ ( w ') ² .                  (7)

R 2

Здесь u – перемещение в направлении оси x , R – радиус кривизны панели. Подставляя (7) в закон Гука (2), получим

Nw 1

— = u '-- + -( w T .

KR 2

Интегрируя (8), найдем выражение для u :

Nxw1x u = —x +   dx -   (w ')2dx + C .

К JR

Из условия закрепления на левой опоре вытекает, что

C = 0.

Для получения уравнения относительно усилия N нужно записать условие закрепления на правом краю панели в виде:

u (L ) = 0.                      (10)

Соотношение (10) является нелинейным уравнением относительно N, которое потребовало бы разработки специальных методов его решения. Поэтому ранее в [7] был предложен другой путь для отыскания связи между N и внешней нагрузкой (в [7] был рассмотрен только вариант равномерно распределенной нагрузки q ). Следуя этому подходу, и здесь можно принять, что внешние воздействия меняются пропорционально некоторому параметру нагружения t , а именно:

F = F o • t , q = q о • t .                 ⁽¹¹⁾

Тогда с учетом (9) и (5) соотношение (10) при заданном N будет представлять собой квадратное уравнение относительно t . Задавая различные значения для усилия N , можно из (10) выразить корни t через N , а значит, и величины нагрузок по соотношению (11). Таким образом, получим t как функцию параметра N . Подставляя N и t в систему уравнений, полученную из (5) при разных 5 w i , и решая ее, найдем искомые A i . Тогда становятся известными выражения для прогиба (6).

• 2.    Численные эксперименты

Ниже приведены результаты численных экспериментов в случае использования некоторых конкретных геометрических и механических характеристик. Анализировались зависимости между различными параметрами напряженно-деформированного состояния. В качестве первого тестового примера рассмотрим простую задачу о потере устойчивости арки с первоначально постоянной кривизной под действием равномерно распределенной нагрузки q. Решение такой задачи, как следует, например, из работы [2], может быть сведено к расчету критической нагрузки для кольца. Оно записано в виде [2]:

_ EJ ( 4п2 R2

Чкр = R3 I L2

Здесь Е – модуль Юнга, R – радиус кривизны арки.

В качестве фi (x), входящих в ряд (5), в этом случае удобно использовать тригонометрические функции вида фi( x) = sin( inx / L).(13)

Они удовлетворяют не только кинематическим условиям шарнирного закрепления, но и статическим, а именно изгибающие моменты на торцах арки будут также равны нулю.

Были исследованы арки различной геометрии с различным числом членов ряда в (5). Оказалось, что результаты, полученные при удержании даже двух (5), отличаются менее чем на 4,8 % от результатов, полученных при большем количестве членов ряда. Таким образом, в этой задаче достаточно ограничиваться двумя первыми функциями (13).

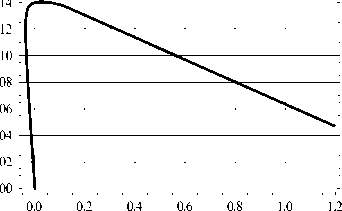
Для расчетов были приняты следующие исходные данные: L=10 м, R=12,5 м, EJ= 0,45 МН м2. Тогда формула (12) дает значение q кр = 0,1398 МН/м. С этим ре- зультатом хорошо согласуется полученная по приведенной выше методике и приведенная на рис. 2, а, зависимость q = q (w1), где w1 - это прогиб на расстоянии 0,5 L от левой опоры.

a

b

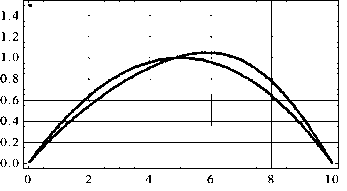
Рис. 2. Зависимость q = q ( w 1 ), w 1 = w (0,5 L ) ( а ); формы арки до загрузки и после потери устойчивости ( b )

Fig. 2. Dependence q = q ( w 1 ), w 1 = w (0.5 L ) ( a ); arch shapes before loading and after loss of stability ( b )

Далее была рассмотрена задача о нагружении арки сосредоточенной силой F1, приложенной в некоторой точке x1 (см. рис. 1). Такая задача исследовалась в [8] на основе анализа нелинейного дифференциального уравнения равновесия четвертого порядка. Полученные решения слева и справа от точки приложения силы стыковались в [8] путем удовлетворения в этой точке статических и кинематических условий. Была получена также и приближенная формула для критической силы в случае центрально приложенной силы. Она имеет следующий вид:

^f 0 ^D

^F кр     _{3 b} 2

Для этого случая нагружения здесь была рассмотрена задача для панели с теми же исходными данными, что и в первом тестовом примере. Но при этом при вычислении D коэффициент Пуассона принимался равным нулю. Из (14) вытекает следующее значение для критической силы

F _kp = 0,0644 МН.

Ниже приведены результаты, полученные численно по приведенной выше методике. Расчеты дают значение F _kp = 0,06998 МН, отличающееся от полученного по формуле (14) на 7,9 %. Здесь также были исследованы арки различной геометрии с различным числом членов ряда в (5). Оказалось, что здесь необходимо не менее трех членов ряда. Тогда результаты, полученные при удержании трех, четырех и пяти членов ряда (5), отличаются не более чем на 2,5 %. Таким образом, в этой задаче достаточно ограничиваться тремя первыми функциями (13).

b

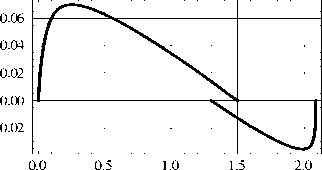
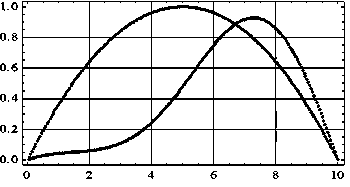
Рис. 3. Зависимость F = F ( w 1 ), w 1 = w (0,5 L ) ( а ); формы арки до загрузки ( b ) и после потери устойчивости

Fig. 3. Dependence F = F ( w 1 ), w 1 = w (0.5 L ) ( a ); arch shapes before loading and after loss of stability ( b )

Здесь наблюдается эффект, который не обнаруживался в [7] при равномерной нагрузке, но имеет место при воздействии сосредоточенной силы. А именно, как видно из рис. 3, при кинематическом нагружении (когда сила F является фактически реакцией) после прохождения верхней критической нагрузки, равной

F cr = 0,06998 МН, в арке достигается состояние нейтрального равновесия, при котором F = 0 . При этом становится возможным существование бесконечного числа форм равновесия. В этом состоянии продольная сила достигает максимально возможной величины N = 0,1772 МН. При дальнейшей деформации арка выворачивается, а силу F требуется уже направлять не вниз, а вверх (т.е. придерживать арку).

Далее были рассмотрены задачи о деформации арок на упругом основании. Результаты расчета с разными k приведены на рис. 4. Особенностью этих задач является то, что в случае сосредоточенной нагрузки при больших коэффициентах постели k для сходимости решения требуется уже большее число слагаемых в ряду (5), чем в предыдущем случае. Еще одной особенностью таких задач является то, что при немалых k уже не происходит потери устойчивости (т.е. нет предельной точки, как на рис. 2 или на рис. 3). Однако возможна ситуация, когда на диаграмме F = F ( w 1 ) появляется почти горизонтальный участок. Такая диаграмма напоминает зависимость сжимающей силы от осевого перемещения в задаче о за-критическом изгибе прямого стержня (см. задачу об эластике Эйлера, например, в [1]). Третьей особенностью является то, что в рассмотренных задачах даже при малых k не обнаружено эффекта, отмеченного выше для свободно опертой арки, когда становится возможным существование бесконечного числа форм равновесия.

0.20

0.15

0.10

0.05

b

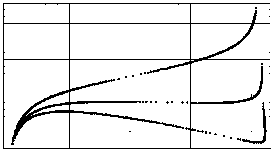
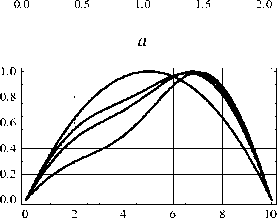
Рис. 4. Зависимость F = F ( w 1 ), w 1 = w (0,5 L ) при k = 0,0072 МН/м² (нижняя кривая); при k = 0,0177 МН/м² (средняя кривая); при k = 0,0256 МН/м² (верхняя кривая) ( а ); формы арки до загрузки, а также при одной и той же нагрузке F = F 0 , которая равна критической в случае k = 0,0072 МН/м²(нижняя кривая); вторая и третья снизу кривые – формы арки при F = F 0 в случаях k = 0,0129 МН/м² и k = 0,022 МН/м² соответственно ( b )

Fig. 4. Dependence at k = 0.0072 MN/m² (lower curve); at k = = 0.0177 MN/m² (middle curve); at k = 0.0256 MN/m² (upper curve) ( a ); the shape of the arch before loading, as well as at the same load, which is critical in the case of k = 0.0072 MN/m² (lower curve); the second and third curves from below are the shape of the arch in the cases of k = 0.0129 MN/m² and k = 0.022 MN/m², respectively ( b )

Далее были рассмотрены задачи о деформации арок на упругом основании с разными коэффициентами постели k под действием центрально приложенной нагрузки F , а также арок переменной толщины на упругом основании при k = 0,0072МН/м². На рис. 5, а , приведены результаты расчета с различными k , а на рис. 5, b – для разных законов изменения толщины по длине арки. Как и ожидалось, увеличение k ведет к повышению жесткости арки (см. рис. 5, а ). А анализ решений при разных законах изменения толщины арки приводит к не совсем предсказуемому результату.

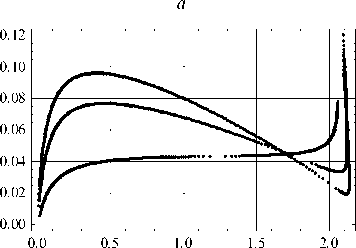
b

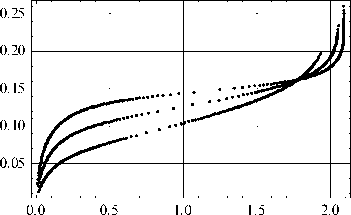
Рис. 5. Зависимость F = F ( w 1 ), w 1 = w (0,5 L ) при k = 0,0072 МН/м² (нижняя кривая); при k = 0,0177 МН/м² (средняя кривая); при k = 0,0256 МН/м² (верхняя кривая) ( а ); зависимость F = F ( w 1 ) при k = 0,0072 МН/м²; для нижней кривой отношение изгибной жесткости в центре арки к изгибной жесткости на опорах равно 0,3; для средней кривой равно 1; для верхней кривой равно 1,4 ( b )

Fig. 5. Dependence F = F ( w 1 ), w 1 = w (0.5 L ) at k = 0.0072 MN/m² (lower curve); at k = 0.0177 MN/m² (middle curve); at k = 0.0256 MN/m² (upper curve) ( a ); dependence F = F ( w 1 ) at k = 0.0072 MN/m²; for the lower curve, the ratio of the bending stiffness in the center of the archto the bending stiffness on the supports is 0.3; for the middle curve, it is 1; for the upper curve, it is 1.4 ( b )

Для изгибной жесткости был принят следующий закон ее изменения по длине арки: