Бортовой пылеударный масс-спектрометр для исследования элементного состава микрометеороидов

Времяпролетные масс-спектрометры находят широкое применение для решения ряда задач при проведении космических экспериментов, для изучения химического состава космической пыли, космического мусора, собственной атмосферы космических аппаратов, грунта космических объектов, газопылевых хвостов комет и т. д.

Так, например, пылеударные масс-спектрометры используются для анализа микрометеорит-ных потоков [1–3]. В таких масс-спектрометрах ввиду большого энергетического разброса ионов, возникающих в результате ударного взаимодействия частицы-ударника и мишени, как правило, достаточно высокую разрешающую способность получают путем использования больших ускоряющих напряжений (порядка 1–1.5 кВ) [1–4].

В соответствии с известными данными о распределении микрометеороидных потоков в околоземном пространстве и дальнем космосе, а именно ввиду малой вероятности ударных взаимодействий пылевых частиц с мишенью прибора, рабочая площадь чувствительной поверхности пылеударного масс-спектрометра должна быть как можно большей при сохранении характеристик прибора. Авторами предложены реализации конструкций, которые должны удовлетворять следующим требованиям:

– минимизация зависимости выходных характеристик от места соударения;

– высокая разрешающая способность;

– высокая чувствительность;

– минимизация габаритно-массовых характеристик спектрометра.

МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ФОКУСИРОВКИ В ПЫЛЕУДАРНОМ МАСС-СПЕКТРОМЕТРЕ

На основе вышеприведенных требований, предъявляемым к приборам, которые используются при проведении космических экспериментов, с целью обеспечения взаимопротиворечивых характеристик были разработаны две конструкции ″аʺ и ″б″ пылеударного масс-спектрометра, приведенные на рис. 1, со следующими расстояниями между сетками:

1 12 = 5 - IO " ³ м;    1 _бп = 245 - 10 — ³ м;

1 ₃₄ = 1 ₄₅ = 1 56 = 10 . 10 ^{- 3} м ; 1 67 = 83.5 - 10 ^{- 3} м ;

1 ₇₈ = 12.5 - 10 ^{- 3} м.

В традиционных конструкциях масс-спектрометров бесполевое пространство располагается перед мишенью [5, 6]. В предлагаемых конструкциях масс-спектрометров в мишени выполнены прорези, пропускающие ионы из одной части конструкции в другую. Особенностью конструкции, приведенной на рис. 1, является мишень с системой равномерно расположенных отверстий,

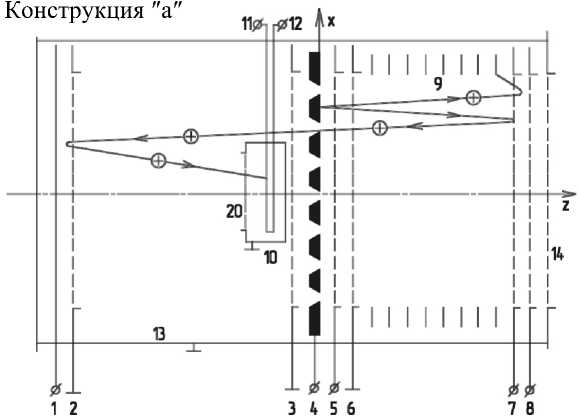
Конструкция ″б″

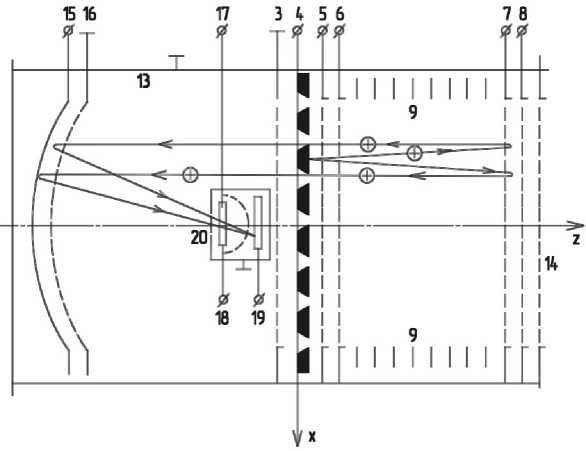
Рис. 1. Конструкции масс-спектрометра.

(1, 2) — отражатель ионов, причем на сетке 2 нулевой потенциал, на пластине 1 Uотр = 145 В; (2, 3) — сетки, ограничивающие бесполевое пространство; 4 — мишень с потенциалом +UM = 100 В; (4, 5) — ускоряющий промежуток, на сетке 5 потенциал Uуск = –300 В; (5, 6) — гасящий промежуток, служащий для уменьшения энергии ионов и растягивания спектра во времени, на сетке 6 нулевой потенциал; (6, 8) — фокусирующее зеркало; (6, 7) — первый рефлектор фокусирующего зеркала, на сетке 7 потенциал +U1 = 125 В; (7, 8) — второй рефлектор фокусирующего зеркала, на сетке 8 потенциал +U2 = 145 В; 9 — система колец, служащая для создания линейного изменяющегося потенциала в области первого рефлектора; 10 — корпус приемника с микроканальной пластиной (МКП); 11 — собирающий потенциал приемника Uсоб = = –300 В; 12 — питающий потенциал МКП; 13 — корпус датчика с входным окном 14; (15, 16) — параболический отражатель ионов, причем на электродах 15 и 16 потенциал, соответствующий потенциалам системы (1, 2); 17 — корректор разрешения; 18 и 19 — возможные положения приемника конструкции ″б″; 20 — входное отверстие приемника минимизирующая эффект затенения приемника. В основе конструкции ″б″ лежит свойство параболоида: длина каждой траектории, параллельной оси Z, не зависит от места соударения частицы ударника и мишени и равна длине бесполевого пространства в конструкции ″а″, рефлектрон рассчитан в соответствии с методикой, приведенной в [7].

С целью верификации полученных характеристик приборов было произведено моделирование работы масс-спектрометров с использованием уравнений движения заряженных частиц в электростатических полях. Для расчета электростатических полей внутри прибора был применен экс- траполяционный метод Либмана, предложенный Франкелом [8], Янгом [9], который является наиболее универсальным и полезным из всех быстро сходящихся итерационных методов. Этот метод эквивалентен последовательной узловой релаксации с перебором (отсюда название экстраполяционный). Он представляет собой развитие метода Либмана, основанное на введении коэффициента a:

• n + 1 _ дп

A n , k = A n , k +

• a n         n         n         n         2          n

+ 4 ( A n + 1, k ⁺ A n , k + 1 ⁺ A n - 1, k ⁺ A n , k - 1 ⁺ h W A n , k ) ^.    (1)

Здесь a является коэффициентом сходимости, или коэффициентом релаксации, определяющим степень перебора. Можно показать, что его значение должно находиться в пределах (1,2). Если a = 1, то уравнение (1) превращается в уравнение для обычного метода Либмана, а при a >  2 процесс решения становится неустойчивым.

При работе с прямоугольными областями можно воспользоваться способом нахождения оптимального значения a , предложенным Янгом [10]:

представления электрического поля в виде матрицы потенциалов можно перейти от частных производных к приращениям (при условии их достаточной малости):

E x

E y

А V »--.

А г

А V

^А У ’

ab

(

2 1 - п

к

П  Г)

2" + 2" p q )

где a b — оптимальное значение коэффициента сходимости; p — количество узлов сетки по вертикали; q — количество узлов сетки по горизонтали.

Рассмотрим связь между потенциалом и напряженностью электрического поля. В результате расчетов мы получили матрицу потенциалов поля. Для расчета траекторий необходимо перейти от потенциала к напряженности электрического поля. В соответствии с уравнением Максвелла в случае

где V — потенциал электрического поля. Расчет траекторий производился с использованием известных уравнений движения заряженных частиц в электрических и магнитных полях.

Численный расчет траектории представляет собой дискретное движение частицы в поле с определенным шагом по времени, но логично предположить, что координаты частицы не будут совпадать с координатами узлов сетки потенциалов. Поэтому необходим уточненный расчет напряженности поля в точке расположения частицы.

Воспользовавшись уравнениями (3) и переходя от дифференциала к приращению времени, получим следующие уравнения, на основе которых будет составляться алгоритм:

б

а

δ сб ∙10^–3

δ сб ∙10^–3

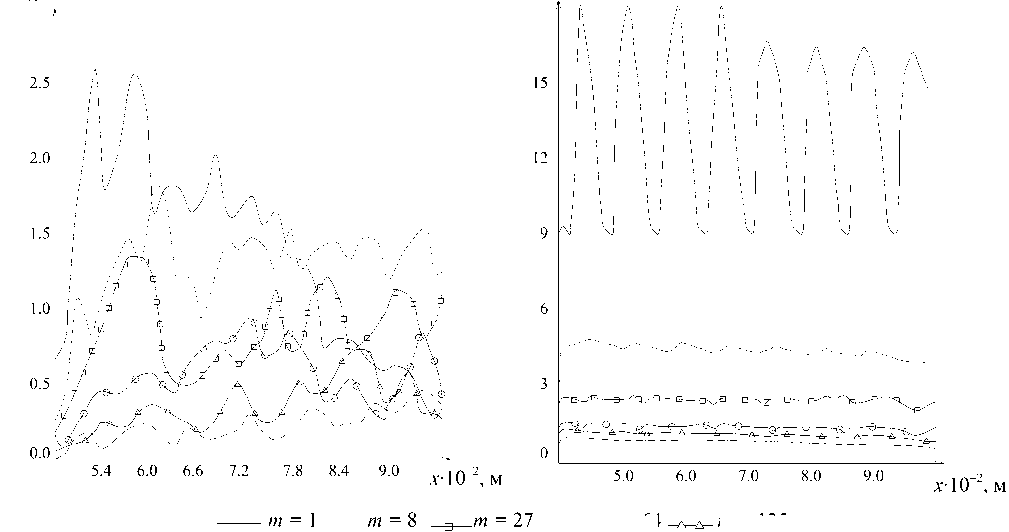
m = 64

m = 125 _{m =} 216

Рис. 2. Зависимость коэффициента сбора δ сб от координаты удара и массы ионов для конструкций ″а″ и ″б″. (Коэффициент сбора равен отношению принятых приемником ионов к общему количеству ионов δ _сб = N _пр / N _общ)

1     , . qE_ . 1 .

x ( t + A t ) = x ( t ) + 1 v_x ( t ) + -^x- A t IA t ,

• V      m

(      qE„1

y ⁽ t + ^A t ) = y ⁽ t ) + v y ⁽ t ) +----^A t ^A t ,

• V       m)

  
  

где v x , v y — соответственно горизонтальная и вертикальная составляющие скорости частицы в текущий момент времени.

Вопрос выбора шага времени A t достаточно сложен, однако нужно заметить, что выбирать A t необходимо так, чтобы приращение координат ( x или y ) было хотя бы на порядок меньшим, чем шаг сетки потенциалов. Таким образом, необходимо выводить расчетное Δ t во время полета частицы для возможности корректировки входного шага по времени Δ t op , задаваемого оператором.

Результаты расчета коэффициентов сбора (см. определение в подписи к рис. 2) в зависимости от места соударения для конструкций ″а″ и ″б″ соответственно приведены на рис. 2, а, и рис. 2, б. (диаметр МКП — 56 мм, диаметр диафрагмы — 1 см).

Результаты моделирования зависимости разрешения конструкций масс-спектрометров от массы и координаты удара приведены на рис. 3: кривые, маркированные 1, — конструкция ″а″; кривые с маркой 2 — конструкция ″б″; кривые 3 — конструкция ″б″ со сферическим корректором.

Как видно из рис. 2 и 3, конструкция ″а″ позволяет получить довольно высокое разрешение, не зависящее от координаты х . Однако из рис. 2 видно, что конструкция ″а″ обладает небольшим коэффициентом сбора водорода ( m = 1) при большой площади приемника, а также большим разбросом коэффициента сбора для разных точек мишени. Недостатком данной конструкции является различный характер зависимостей коэффициентов сборов для каждой массы от координаты х . Конструкция ″б″ позволяет избежать вышеприведенных недостатков конструкции ″а″. Расчетные параметры данной конструкции приведены на рис. 2 и 3. Из этих рисунков видно, что достоинством конструкции ″б″ является незначительный разброс значений коэффициента сбора, не зависящий от координаты удара x . Разрешение конструкции ″б″ невысоко и зависит от координаты х , что показано на рис. 3. Такое ухудшение разрешения объясняется тем, что не все траектории ионов параллельны оси Z.

Для устранения ухудшения разрешения, вызванного наклоном отражателя относительно приемника, используется диафрагмирование приемника и применение сферического корректора. Один из вариантов такой конструкции представлен на рис. 4.

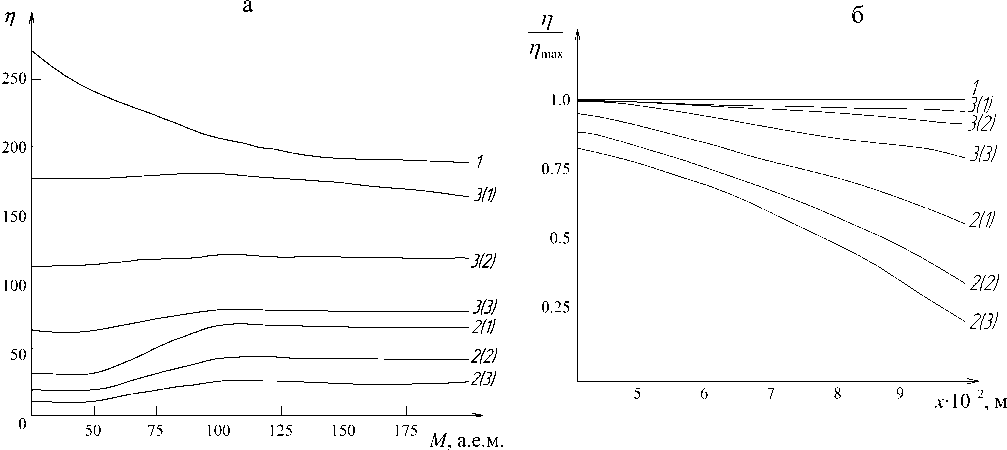
Рис. 3. Зависимость разрешения конструкции от массового числа и координаты удара.

2 (1) — dg = 1.5·10–2 м (dg — диаметр отверстия диафрагмы); 2 (2) — dg = 1.0·10–2 м; 2 (3) — dg = 0.7·10–2 м;

3 (1) — dg = 1.5·10^–2 м; 3 (2) — dg = = 1.0·10^–2 м; 3 (3) — dg = 0.7·10^–2 м; х = 10 см

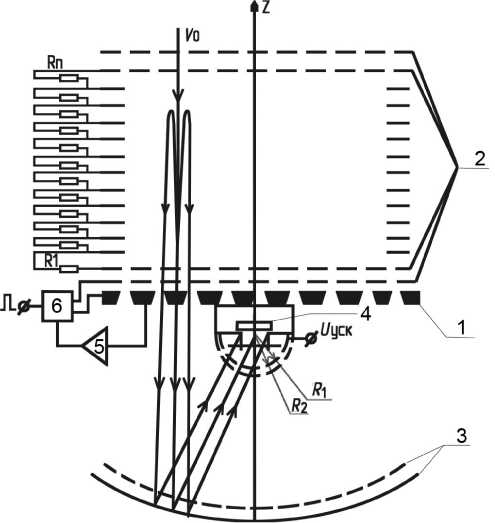
Рис. 4. Конструкция ″б″ с диафрагмой перед приемником ионов и сферическим корректором

1 — мишень; 2 — электростатическое зеркало; 3 — параболический отражатель ионов; 4 — приемник ионов; 5 — усилитель-формирователь; 6 — блок формирования выталкивающего импульса

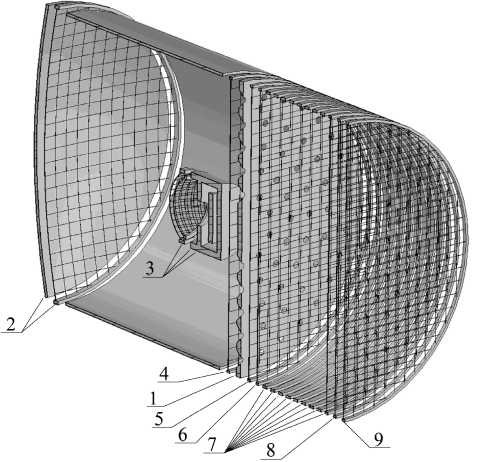
Рис. 5. 3D-модель конструкции ″в″.

1 — мишень; 2 — параболический отражатель; 3 — приемник ионов со сферическим корректором; 4 — сетка, ограничивающая бесполевое пространство; 5 — ускоряющая сетка; 6 — гасящая сетка; 7 — первый рефлектор зеркала, состоящий из восьми колец и сетки; 8 — сетка второго рефлектора; 9 — входная сетка

При оптимальном сочетании диаметра сферы и диафрагмы, а также диаметра MКП и ее расстояния до сферы можно значительно улучшить разрешение без ухудшения других характеристик блока. Радиусы сеток R 1 и R 2 выбираются с учетом соотношения

R -R

0.1 < -¹---- ² <  1.                 (5)

—

Такая конструкция ″в″ обладает характеристиками, превосходящими характеристики конструкций ″а″ и ″б″.

Моделирование конструкции было произведено для трех координат, 3D-модель конструкции приведена на рис. 5.

Результаты моделирования зависимости разрешения конструкции ″в″ от массы и координаты удара приведены на рис. 6, а, б, соответственно.

РЕЗУЛЬТАТЫ УДАРНЫХ ЭКСПЕРИМЕНТОВ

На основе проведенного моделирования был создан масс-спектрометр, показанный на рис. 7.

Его схематическое изображение представлено на рис. 4. Масс-спектрометр содержит мишень 1 с выполненными в ней отверстиями. На поверхность мишени нанесена серебряная пленка. Со стороны ударяющих в мишень частиц установлено электростатическое фокусирующее зеркало 2, а с другой стороны — параболический отражатель ионов 3 , фокусирующий их на приемник 4. Образовавшиеся при ударе ионы выталкиваются импульсом, сформированным в промежутке мишень—сетка. Электронный импульс, образованный при ударе на мишени, через усилитель-формирователь 5 запускает блок формирования 6 выталкивающего импульса.

Образец бортового прибора для проведения лабораторных испытаний, показанный на рис. 7, обладает следующими характеристиками: общая длина 280 мм, диаметр прибора 240 мм, масса 1.3 кг, суммарная потребляемая мощность ~7 Вт (вместе с блоком обработки ионных спектров).

Диапазон ускоряемых частиц по скоростям составлял 1–20 км/с. Эксперименты выполнены с помощью электродинамического ускорителя [11] и генератора Ван де Граафа согласно методике, подробно описанной в [12].

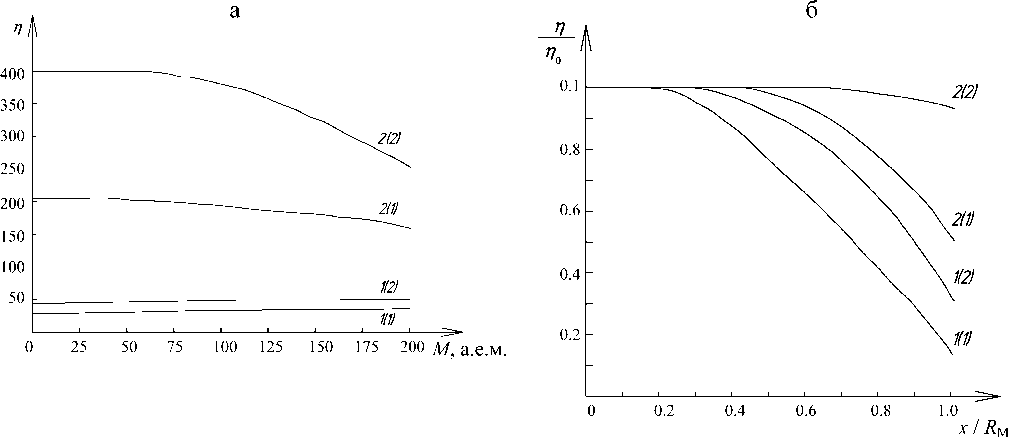
Рис. 6. Зависимость разрешения конструкции от массового числа (а) и координаты удара (б).

Кривая 1 — конструкция ″б″ со сферическим корректором; кривая 2 — конструкция ″в″ с оптимальными параметрами приемника; 1 (1) — dg = 1.0·10^–2 м (dg — диаметр отверстия диафрагмы); 1 (2) — dg = 0.7·10^–2 м; 2 (1) — dg = = 1.0·10^–2 м; 2 (2) — dg = 0.7·10^–2 м. x — расстояние от оси прибора до места соударения: R _M — максимальное расстояние от оси прибора до места соударения, равное радиусу мишени

Рис. 7. Внешний вид газопылевого масс-спектрометра

Регистрация ионных спектров проводилась с помощью запоминающего осциллографа. Параллельно спектры записывались в память блока обработки. Информацию о скорости частиц и их зарядах получали с помощью кольцевых индукционных датчиков. За начало процесса развертки ионного спектра принимался фронт импульса электронов с мишени 1 (рис. 4).

На рис. 8 представлены ионные спектры, полученные ударом частиц из Fе и SiO 2 в ниобиевую мишень. Диапазон скоростей частиц находился в пределах 0.2–20 км/с.

На рис. 8, а, в спектре наблюдаются ионы, присутствующие в остаточном газе вакуумной камеры (H2O+ , N2+ , O2+ , H2+ , N+ , CO2+ ) , а также в материале мишени (Nb) Zi+, Н+, Nа+, Al+, K+, Cu+, O+. Наличие ионов в диапазоне скоростей частиц 0.2–2 км/с обусловлено электрическим разрядом, возникающим между заряженной частицей и мишенью при малом расстоянии между ними. При снятии заряда частицы электронным пучком при ее скорости 0.2–2 км/с ионы в спектре не наблюдаются. Таким образом, при низких скоростях частиц действует потенциальный механизм образования ионов.

Согласно принципу ускорения электростатическим способом, большей скорости частицы соответствует ее меньший размер и меньший заряд, поэтому при V = 2–4 км/с в момент разряда частицы за меньший промежуток времени на мишень образуется меньше ионов, что видно на рис. 8, б.

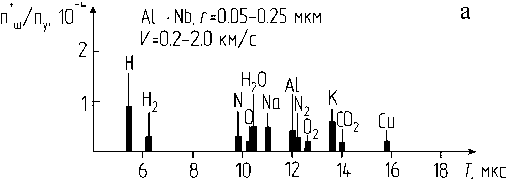
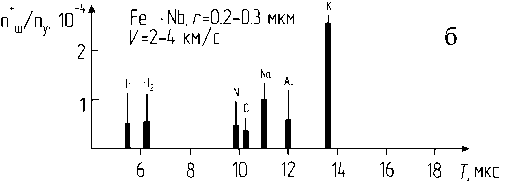
18 Т, мкс

в

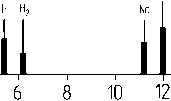
Fe— Nb, /'=0.2-03 мкм М-13 км/с

18 Т, мкс

г

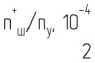
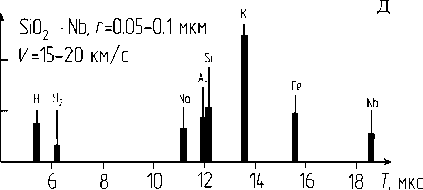
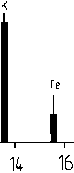
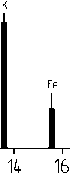
Рис. 8. Ионные спектры с масс-спектрометра, полученные с помощью электростатического ускорителя в диапазоне скоростей частиц 0.2–20 км/с

Ударный механизм взаимодействия является определяющим при скоростях частиц более 6 км/с (рис. 8, в, г, д). При увеличении скорости частицы до 8 км/с в спектре ионов появляется Fe+.

Другой важной характеристикой пылеударного масс-спектрометра является зависимость спектров ионов от места соударения частицы с мишенью. Для уменьшения этой зависимости в мишени равномерно по ее площади выполнены отверстия ∅ 3 мм. Отверстия в мишени имеют форму конуса для увеличения пропускной способности ионов. Параболический отражатель 3 (рис. 4) практически независимо от места соударения фокусирует ионы на приемник 4 . Качество фокусировки (сбора ионов) зависит от точности изготовления отражателя. Все металлические детали масс-спектрометра выполнены из нержавеющей стали, а отражатель — из ниобия.

ЗАКЛЮЧЕНИЕ

Полученные результаты позволяют сделать вывод о том, что применение параболического отражателя в масс-рефлектроне позволяет значительно уменьшить зависимость масс-спектров от места соударения частицы и мишени. Для достижения этого результата, однако, требуется диафрагмирование приемника, вызывающее некоторое падение коэффициента сбора ионов.

Достоинствами конструкции являются:

– малые габариты;

– малые вытягивающие напряжения;

– малое энергопотребление.

Проверка конструкции была проведена с помощью электродинамического усилителя и генератора Ван де Граафа. Прибор показал работоспособность в широком диапазоне скоростей частиц, а также соответствие результатов численного моделирования параметрам конструкции, полученным экспериментально.