Brain Tumor Boundary Detection by Edge Indication Map Using Bi-Modal Fuzzy Histogram Thresholding Technique from MRI T2-Weighted Scans

Published Online September 2016 in MECS

Medical imaging provides a reliable source of information of the human body to the clinician for use in fields like reparative surgery, radiotherapy treatment planning, stereotactic neurosurgery etc. [1]. The diagnosis of human being organs has been improved significantly with the arrival of Computed Tomography (CT), Magnetic Resonance Imaging (MRI) and Positron Emission Tomography (PET) techniques. MRI is the preferred procedure for diagnosing a large number of potential problems or abnormal conditions in many different parts of the body. MRI is a non-destructive testing technique and safe modality for medical imaging that uses the magnetic field and pulses of radio waves [2].

(a)

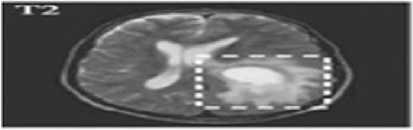
(b)

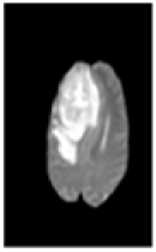
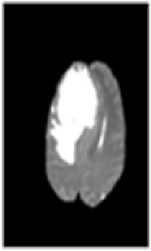
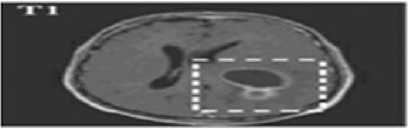
Fig.1. (a) Brain tumor in T1 weighted (b) Brain tumor in T2 weighted

It gives better visualization of soft tissue in human body. In general, MRI creates images that can show differences between healthy and unhealthy tissues. Physicians use MRI to examine the brain, spine, joints (e.g., knee, shoulder, hip, wrist and ankle) abdomen, pelvic region, breast, blood vessels, heart and other body parts [3].

Two types of MRI brain images used in common as T1 weighted and T2 weighted. The normal MRI brain image contains major three components as white matter (WM) tissues, gray matter (GM) tissues and cerebrospinal fluid (CSF) [4]. T1-weighted provides good contrast between WM tissues in light gray and GM in dark gray, while CSF is void of signal as black intensity. T2-weighted provides good contrast between CSF (bright) and brain tissues (dark). A brain tumor is abnormal tissues growth in the brain. The abnormal MRI brain image having an additional region as tumor exhibits mixed intensities levels in T1-weighted and hyper intensities in T2-weighted [5] as shown in Fig. 1. Brain tumors classified as two major type as: benign (non-cancerous) called primary brain tumor and malignant (cancerous) called as secondary brain tumor [6]. A benign tumor does not contain cancer cells and once removed, does not reappear. Most benign brain tumors have clear borders without having any surrounding tissues. Malignant brain tumors contain cancer cells. Malignant brain tumors does not have clear boundary because they occupy by surrounding tissues like edema, active tumor and necrotic [7]. Tumor boundary detection is very sensitive during the surgical processes. Normal brain tissues considered as tumor cells during surgery might affect the entire brain functionality. In otherwise, the left over tumor tissues cause some risk. So the exact tumor boundary, the border between normal and abnormal brain tissues, detection is necessity of the surgical process.

In digital images, the edge occurs when intensity changes abruptly. Each traditional edge detector has their own property to detect the intensity variation from neighborhood pixels. In some kind of edge detectors, known edges were not shown in the result and removing the spurious edge is very tedious [8]. One major challenge in the brain tumor boundary detection process is they do not have clear boundaries because they sometimes surrounded by tumor substructures. The popular well known edge operators are directly applied to T2 weighted image to target the tumor boundary and the results are shown in Fig. 2.The tumor boundary is not clearly obtained using traditional edge detectors like Robert, Prewitt, and Sobel. More number of false edges occurred in the result of Canny and Marr-Hildreth.

The proposed work focused to extract brain tumor boundary along with brain substructures like CSF, sulcal CSF (SCSF) and interhemispheric fissure to 3D volume construction and visualization. The proposed method is initiated by bimodal fuzzy histogram thresholding for obtaining the threshold value. Then the threshold is used by piecewise linear transformation for enhancing the tumor region. Next the edge indication map (EIM) was generated by applying the maximum voting scheme on results of various edge operators. The EIM has given tumor boundary in relative to brain border and some of its

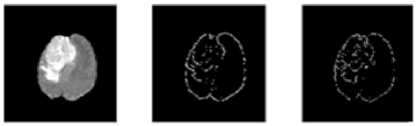
(a)                       (b)                         (c)

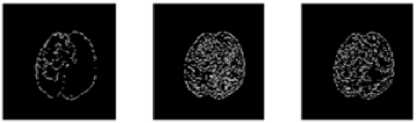
(d)                         (e)                           (f)

Fig.2. Output of MRI brain image using various edge detection operators (a)Original image (b) Robert (c) Prewitt (d) Sobel (e) Canny (f) Marr- Hildreth substructures. Evaluation parameters are used for comparing proposed method with gold standard and standard edge detection methods. Finally EIM based 3D volume construction done using 3D doctor [9].

This paper includes the section II as literature survey. The section III contains methodology of proposed work. Section IV has the evaluation parameters. Section V contains results and discussion. Section VI concludes the paper.

• II.    Related Work

Several methods have been developed in brain image segmentation [10] [11] [12]. K. Somasundaram and T. Kalaiselvi [13] proposed a technique to detect the tumor from MRI head scans. They segmented the brain into regions like WM, GM, CSF and background using FCM algorithm. They used extended maxima transform for separating the tumor region from the normal CSF region. Sabbih et al., [14] summarized the comprehensive review of the methods and techniques used to detect the brain tumor through MRI image segmentation. Kalaiselvi et al., [15] present a fusion based technique that produced robust and fully automatic tumor extraction for magnetic resonance images (MRI) of Head scans. They used three popular deformable methods, snake, level set and distance regularized level set for predicting their performance in generating the brain tumor boundaries. A work done by Zolqernine et al., [16] summarized the comparison of Canny and Sobel edge detection in MRI images. Sobel method used with 3 x 3 masks while canny used adjustable mask. They proved that Sobel edge detection method cannot produce smooth and thin edge compared to Canny method.

Kalaiselvi et al., [17] finding the brain contours to detect the boundary between the hemispheres to joining the edges of the two portions of cleft that corresponds to inter-hemispheric fissure present in the contour. The detected boundary is used to separate the cerebrum into two hemispheres and thus found the tumor location. A work done by Subhro and Ardhendu [18] summarized the edge detection techniques and differentiate their efficiency based on their finding suitable to meaningful edges of medical images. Xie et al., [19] proposed a method to detect the boundary of tumor by using the Canny edge detection algorithm and labeling the 8-connected edge with a different number. Then the histogram plotted based on the size of the edge. Finally the weak edge detected by the histogram segmentation is used to find the brain tumor edge. A work done by Riries and Khusnul [20] detecting the brain tumor edge, using the techniques Robert, Prewitt and Sobel method. In this method, they analyzed the best among three, based on their mean and standard deviation value. From the three Sobel method gave the smaller standard deviation value and produced the good pattern of brain tumor.

A work done by Manoj et al., [21] proposed a new method for edge detection using Cellular Automata. The Cellular Automata rule provides strong and continuous edge detection. The proposed method provided the clear, fine and continuous edges and also no extra pixels detected in brain tumor. A work done by Mamta and Parvinder [22] summarized the edge detection techniques and its performance by studying the edge maps relative to each other through statistical evaluation. They used the first order derivative based edge detection (Gradient Method) and second order derivative based edge detection (Laplacian based edge detection). A statistical approach done by Amiya et al., [23] proposed a method which based on the neighborhood pixels using a predefined intensity range and simple statistical approach. In this approach, they determined all edge pixels of image and removed noise from the output edge map.

• III.    Proposed Method

The flowchart of the proposed work is given in Fig. 3. The proposed work has two major steps. Initially step 1 is aimed to enhance the contrast in order to make the sharp edges. An intensity transformation is used for contrast enhancement with automatic threshold value produced by bimodal fuzzy histogram thresholding technique. Next in step 2 the EIM is generated by hybrid approach with the results of existing edge operators and maximum voting scheme. Since the work is histogram based the unwanted non-brain portion are removed initially. This is known as brain extraction process and done by BEA [24]. The extracted brain is then focused for further processing like intensity transformation and edge detection. The intermediate techniques like histogram smoothing, bimodal fuzzy histogram thresholding, piecewise linear transformation and edge indication map are explained in the following section.

• A.    Histogram Smoothing

For an image I with size M × N and L number of gray levels, the histogram can be expressed as:

н — i = 0,1,2,..... ,L-1      (1)

where, Н is the histogram vector, ht is number of pixels of gray level i and L ismaximum number of possible gray levels in the image. Original histogram has more number of peaks. Histogram smoothing is done by Gaussian distribution expressed as:

_ (X- Ц) ² f ^(x| u, o²) ^——e   ² - ^{2              (2)}

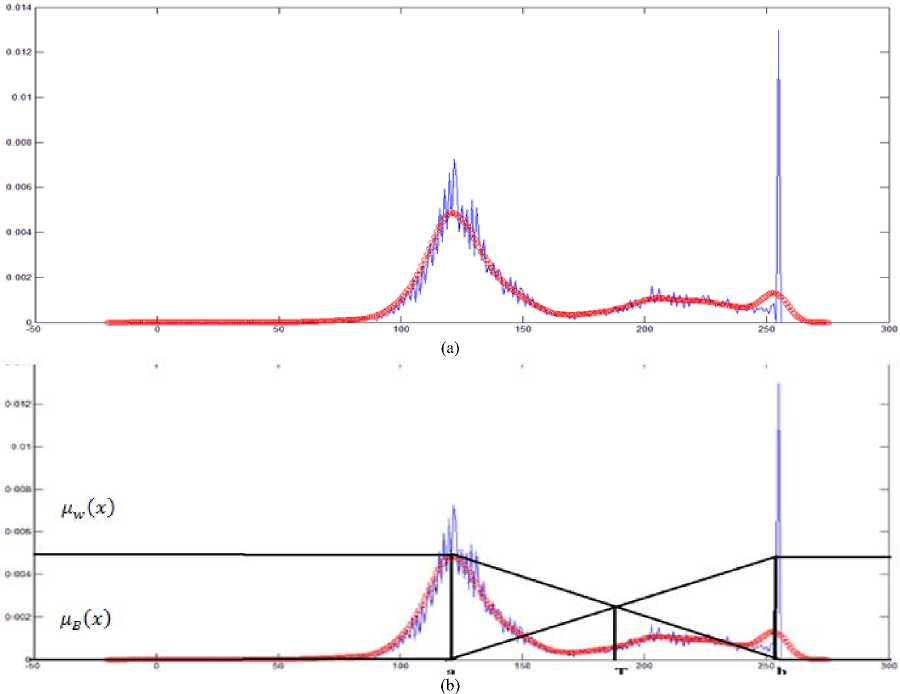
where, µ is the mean and σ2 is variance with the default values (0, 5) is given in Fig. 4 (a). Tumor region and CSF having higher intensities in the T2 weighted MRI than other tissues. GM and WM are lesser gray levels than tumor region. Fuzzy bimodal thresholding produces threshold value based on top two peak values from the histogram. One peak coming from tumor and CSF region another one is from GM and WM region as shown in Fig. 4(b).

• B.    Bimodal Fuzzy Histogram Thresholding

  Fuzzy logic was proposed in 1965 by Zadeh in his research Fuzzy Sets [25]. Zadeh defined the fuzzy sets and fuzzy logic in additional the membership function which assign each grade to a value between one and zero and introduced the theoretical background. This thresholding method required two membership function based on two peak value from the histogram. The bimodal fuzzy histogram thresholding on the sample image is shown in Fig. 4(b).

Brain extraction process

I

Brain portion image

Histogram smoothing using Gaussian distribution

Bimo dal fuzzy histogram thresholding

Step 1: Image Enhancement

Piecewise Linear Transformation

Enhanced image

Step 2: Edge Indication Map Construction

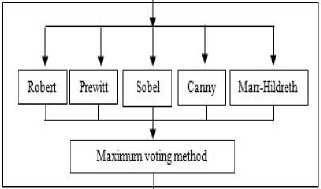
OUTPUT: 2D slices oftumor boundary along with brain border and substructures

Fig.3. Flow Chart for Proposed Method

The histogram is approximated into two membership functions; n_w (x) which measure the white membership value and ц_в (x) which measure how much is the pixel black [26].The value of T can be found in different ways of which is the intersection of the two lines of the membership functions. The membership function can be derived from the Fig. 4(b) is as follow:

ц ^ С^) —

Jx-b ( m xb

0 ) z

hb(^ = |Hj“^         (4)

where, a and b values are automatically obtained from top two peak values of the smoothed histogram. This two membership function fitted to the smoothed histogram as shown in Fig. 4 (b) and the intersection point taken as threshold value T as follows:

T = x; if g_w⁽x) = g_B⁽x)            (5)

Fig.4. (a) Histogram smoothing using Gaussian distribution (b) Bimodal Fuzzy Histogram Thresholding

In the MRI T2- weighted image, tumor region having high intensity values compared to other tissues. Here above the threshold T are consider as tumor region and below the values are normal tissues and background. Threshold T depends on a and b value and vary to each image in the MRI dataset.

• C.    Piecewise-Linear Transformation

Piecewise linear transformation helps to enhance the tumor portion in the output image. This transformation hikes the intensity above T to L-1 and not disturbing other intensity values.

| L - 1, g(x, у) > T I g(x,y), gXx, y) < t

where, g (x, y) is input MRI image, f(x,y) is output piecewise transformed image and L is maximum possible gray value of input image. The sample MRI image and piecewise transformed image are shown in Fig. 5(a) and 5(b). The intensity transformation results in enhance the tumor contrast and thus sharpen its edges. This helps to extract the tumor border efficiently by the following step 2 process.

(a)                           (b)

Fig.5. (a) Original MRI image (b) Piecewise Linear Transformation output image (T=182)

• D.    Edge Indication Map (EIM)

Various edge detection techniques applied to piecewise transform image of Fig. 5(b) and the results are shown in Fig. 6. Each edge operator gives slightly varying tumor boundary position with discontinuity in some places. Here a hybrid procedure is adopted to generate tumor boundary) known as EIM. EIM is one of the hybrid methods from various edge detection techniques handled in Fig. 6. EIM calculated tumor pixels from traditional five edge detection techniques using maximum voting scheme [27]. EIM produces the brain tumor boundary along with brain border as shown in Fig. 6(f).

• IV.    Evaluation Parameters

Various evaluation parameters are used to estimate the performance of the automatic methods against the manual segmentation. In the proposed work we have used the following eight parameters such as percentage of pixels detected (PCO), percentage of pixels not detected (PND), percentage of false alarm (PFA), figure of merit (FOM), distance D⁴₂ , sensitivity, specificity and accuracy to perform the validation. These parameters are mostly depending on the value of TP, TN, FP and FN. True positive (TP), the number of pixels correctly identified as tumor boundary. True negative (TN), the number of pixels correctly detected as background. False positive (FP), the number of pixels falsely identified as tumor boundary. False negative (FN), the number of pixels falsely detected as background.

The percentage of pixels that were correctly detected is P_c0 and is defined as:

Pco = TP/M ax(N_E1M, Ngs) (7)

whereNE1Mrepresents the number of edge pixels in edge indication map, Nssrepresents number of edge pixels in gold standard MRI image. The range of metric lies between 0 and 1. Maximum value is optimal. If Pco value is 1, then its shows the perfect match between the images. Else if its value is 0, then there is no similarity between images.

The percentage of pixels that were not detected is (P_vd) and is defined as:

P_ND = FN/M xxEN_eim, N_gs) (8)

If P_vd value is 0, shows all pixels are correctly detected else all the pixels are not detected. Here minimum value is optimal.

The percentage of pixels that were erroneously detected as edge pixels that is the percentage of false alarm is (P_fa) and is defined as:

P_FA = FP/M xx(Neim,Ngs)         (9)

If E_fa value is 0 there is no error pixel detected else Pj_a value is 1. Here minimum value is optimum.

The Figure of Merit (FOM) of Pratt is another useful measure for assessing the performance of edge detectors. This measure uses the distance between all pairs of points corresponding to quantify with precision, the difference between the contours. The FOM, which assesses the similarity between two contours is defined as:

FOM =

max (VeimVgs)  ¹1+ax d?

d[is the distance between an edge pixel and the nearest edge pixel of the ground truth and α is an empirical calibration constant and was used α =1/9, optimal value established by Pratt [28]. FOM reaches its maximum value one to similar images and dissimilarity gives minimal value.

From the combination of the indices defined by equations (7), (8), (9) and (10) together with the index of merit of Pratt has proposed a new global index, which is defined by Euclidean distance ( D*₂ ), where its coordinates are optimum values achieved by indices , P_VD, F_fa and FOM respectively. The range of metric lies between 0 and 2 where the value 0 represents perfect value to the measure. The distance to this point can be calculated by

D42 = Mo -1)² + (F0M - 1) + P2d + PA_a (11)

Sensitivity or recall or true positive rate computes how much percentage of object pixels correctly detected as object pixel. The range of metrics lies between 0 to 1 and maximum value is optimal. The sensitivity is defined as:

Sensitivity = ——— (12)

Specificity or true negative rate computes how much percentage of background pixels correctly detected as background pixels. The range of metrics lies between 0 to 1 and maximum value is optimal. The specificity is defined as:

(a)                                              (b)                                                  (c)

(d)                                                    (e)                                                     (f)

Fig.6. (a) Robert (b) Sobel (c) Prewitt (d) Canny (e) Maar- Hildreth (f) EIM

Specificity =                  (13)

r j j tn + FP                   ⁷

Accuracy is the proportion of true results. Accuracy gives percentage of how much object and background pixels exactly detected. The range of metrics lies between 0 and 1. If accuracy value is 1 output as exactly same as input. The accuracy is defined as:

FP + tn

Accuracy_{=                      (14)}

TP + TN +FP+FN           v '

• V.    Results and Discussions

  The sample image and tumor data set were collected from the BRATS 2012 T2 weighted 30 datasets [29]. The hardware and software configurations with the testing system of proposed work are Intel Pentium Processor, 2 GB RAM, Windows 8.1 Pro 32 bit and MATLAB.

The qualitative validation is done by generating the tumor border of gold standard and compared with proposed EIM. For qualitative analysis, the Fig. 7 shows results of the proposed method along with existing edge operators on sample slices. The sample slices selected from the BRATS datasets are given in column 2 of Fig.7.Gold standard of each sample slice given in column 3 of Fig.7. The results of proposed method and other existing edge operators Robert, Prewit, Sobel, Canny and Marr- Hildreth are shown in column 4 – 9 of Fig. 7 respectively. Proposed methods gives the clear cut boundaries and less spurious edges compared with others.

The proposed method yields better visual in terms of tumor location relative to brain border and major substructures like ventricle and interhemispheric tissues as shown in Fig.7. This supports the neuro surgeon to reach their targets quickly and easily.

Table 1 shows the results of proposed and existing edge detection methods compared with gold standards of high grade T2 weighted BRATS tumor 20 datasets using evaluation parameters. Table 2 shows the results of proposed method compared with gold standard of low grade T2 weighted BRATS tumor 10 datasets using evaluation parameters. This is obtained by averaging the results of all images in the datasets.

Table 1 and 2 proved that the optimal values are achieved by the proposed method for most of the parameter like PCO, PND, D⁴f2, sensitivity and accuracy. The proposed method lost its values in PFA and specificity due to the extra spurious edges coming from canny edge detector as shown in Fig.7. The proposed method gives less sensitivity due to FN occurred from brain substructures. But this brain substructure helps to identifying the tumor location easily as shown in Fig. 8.

The 3D volume construction done by 3D doctor using the proposed method outputs (EIM) for BRATS HG_4 dataset is shown in Fig. 8 and tumor location marked by circle. The 3D volume results well separate tumor region and its border from other substructures. This visual result must help the surgeions to plan for surgical procedure and to reach out the tumor location relative to other substructures.

Table 1. Evaluation parameters for High Grade BRATS 2012 20 volumes

Method	P CO	P ND	P FA	FOM	D4 f2	Sensitivi ty	Specific ity	Accur acy
Propose d	0.30 52	0.6570	0.6566	0.7117	1.2018	0.3204	0.9835	0.9661
Robert	0.16 40	0.8196	0.8072	0.6144	1.4761	0.1675	0.9798	0.9575
Prewitt	0.24 14	0.7320	0.7072	0.6392	1.3250	0.2499	0.9822	0.9613
Sobel	0.23 99	0.7351	0.6856	0.6161	1.3273	0.2480	0.9828	0.9613
Canny	0.16 71	0.8328	0.4531	0.2764	1.4569	0.1671	0.9878	0.9228
Marr- Hildreth	0.11 41	0.8858	0.7249	0.3476	1.5884	0.1141	0.9812	0.9310

Table 2. Evaluation parameters for Low Grade BRATS 2012 10 volumes

Method	P CO	P ND	P FA	FOM	D4 f2	Sensitivity	Specificity	Accuracy
Proposed	0.2836	0.6864	0.6359	0.6604	1.2347	0.2978	0.9887	0.9731
Robert	0.1729	0.8249	0.7668	0.5817	1.4615	0.1734	0.9865	0.9674
Prewitt	0.2397	0.7533	0.6711	0.6124	1.3273	0.2423	0.9881	0.9711
Sobel	0.2402	0.7543	0.6684	0.6041	1.3280	0.2425	0.9889	0.9699
Canny	0.1568	0.8431	0.4160	0.2415	1.4773	0.1568	0.9921	0.9313
Marr- Hildreth	0.0995	0.9004	0.7214	0.3031	1.6223	0.0995	0.9869	0.9397

BBRATS_T2_LG1  BBRATS_T2_LG  BBRATS_T2_LG  BBRATS_T2_HG2

1                     8                    4                     4

Gold standard

Propose d EIM method

Robert

Prewit

Canny

Marr-Hildreth

Image source

Original Image

Sobel

Fig.7. Proposed methods compared with existing edge detection methods for a set of sample slices selected from BRATS 2012 datasets

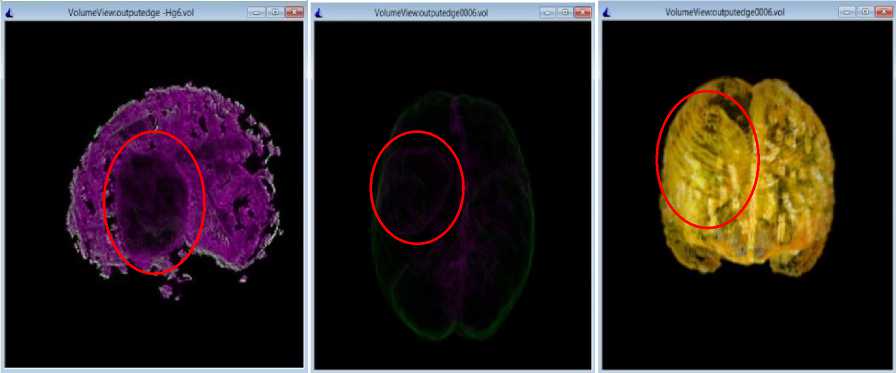
Fig.8. 3D volumes constructed from the results of proposed method for BRATS_HG4 dataset

• VI.    Conclusions and Future Enhancement

Tumor boundary detection is very important process in medical surgical procedure. The proposed work is knowledge based automatic brain tumor boundary detection using fuzzy based histogram and EIM from T2 weighted volumes. This work produced the effective tumor boundary in the abnormal T2-weighted MRI brain image. This method gives better results than standard edge detection techniques. The method also yields tumor border along with brain substructures. This may be helpful to surgeon to reach the exact tumor location. In future, the work is focused to extract the border of edema, active tumor and necrosis for 3D volume construction.