Брэгговские решётки с подавлением паразитного рассеяния для поверхностных плазмон-поляритонов

Одним из перспективных направлений нанофотоники является плазмоника, которая, в частности, изучает свойства поверхностных плазмон-поляритонов (ППП). ППП – это поверхностные электромагнитные волны, распространяющиеся вдоль границы раздела металл / диэлектрик. Величина волнового вектора ППП превышает величину волнового вектора плоской волны, распространяющейся в диэлектрике, а поле ППП локализовано вблизи границы раздела. Указанные свойства обуславливают применение структур на основе ППП в различных практических приложениях, в частности, в плазмонных лазерах [1], нанолитографии [2] и фотовольтаике [3]. Для многих приложений представляет большой интерес управление распространением ППП, т.е. создание различных оптических элементов для ППП, в частности, диэлектрических призм [4], линз [5], волноводов [6], дифракционных решёток [7] и брэгговских зеркал (брэгговских дифракционных решёток) [8].

Однако плазмонные структуры обладают существенными недостатками, такими как потери на поглощение в металле и на паразитное рассеяние, возникающее на границах между различными средами. В [9] был представлен подход к подавлению рассеяния, основанный на использовании анизотропных метаматериалов. Хотя этот подход позволяет полностью исключить потери на рассеяние, проектирование и изготовление метаматериалов с требуемыми параметрами, их интеграция в плазмонные элементы является сложной задачей. В предыдущих работах авторов [10, 11] был предложен простой и эффективный метод подавления рассеяния ППП на диэлектрической сту- пеньке и дифракционной решётке, основанный на переходе к двухслойной конфигурации ступеньки. Такая конфигурация обеспечивает частичное согласование поперечного профиля плазмонных мод в ступеньке и вне её. Было показано, что двухслойная структура позволяет уменьшить потери рассеяния на порядок (до 1–2%). В настоящей работе исследуется возможность применения данного подхода к брэгговским решёткам для ППП, а также обсуждаются альтернативные подходы к уменьшению потерь на рассеяние.

1.    Диэлектрическая брэгговская решётка для ППП

На рис. 1 представлена геометрия брэгговской решётки для ППП, распространяющегося вдоль границы раздела металла с диэлектрической проницаемостью ε m и диэлектрика с диэлектрической проницаемостью ε d . Решётка представляет собой периодический набор диэлектрических ступенек с диэлектрической проницаемостью ε gr , высотой h gr и шириной l 1 , расположенный на поверхности металла. Период решётки – d , расстояние между ступеньками решётки – l 2 = d – l 1 . Длина ступенек в направлении, перпендикулярном плоскости рис. 1, в расчётах полагается бесконечной.

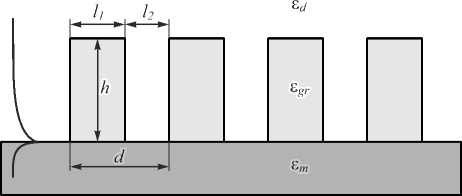
Рис. 1. Геометрия брэгговской решётки для ППП

Параметры брэгговской отражающей решётки l 1 и l ₂ в случае нормального падения ППП (в случае, когда волновой вектор параллелен направлению периодичности решётки) связаны между собой следующим соотношением:

Re( k i ) l i + Re( k 2 ) 1 2 = n (2 m + 1), m = 0,1, 2,...,

где k 1 , k 2 – константы распространения плазмонных мод в области ступеньки и вне её соответственно. Константа распространения k 2 определяется из дисперсионного соотношения ППП:

k 2 = k 0

8 m 8 d8 m + 8 d

Константу распространения k 1 можно определить из дисперсионного соотношения TM-поляризованной моды плоскопараллельного волновода [12,13]:

tanh ( y gr h gr ) =

Ygr 8gr (sd Ym +8m Yd ) 8 d 8 m Ygr +82r Yd Y m  ,

где y 2 = k 1² - k 0 8 j , j = m , d , gr , k ₀ = 2 п / X , X₀ - длина

волны в свободном пространстве. При высоте решётки h_gr >>  5 gr , много большей глубины проникновения ППП в материал решётки, найденное из (3) значение k 1 хорошо согласуется с формулой

k i * k 0

8 m 8 gr8 m +8 gr

.

Одно из решений (1) для параметров l 1 и l 2 имеет вид

Re( k i ) l i = Re( k 2 ) 1 2 =

n( 2 m +1)

m = 0,1, 2,....

Из (5) получаем следующие значения параметров:

l =X 0 (2 m + 1)/4Re( k/k 0 ), i = 1,2.             (6)

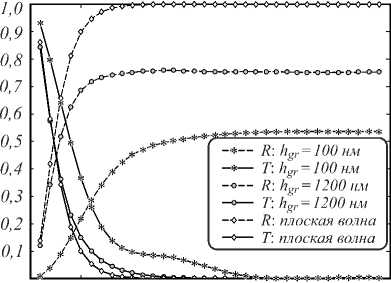
Перейдём к рассмотрению различных примеров брэгговских решёток для ППП. Рассмотрим сначала структуру с параметрами, аналогичными структуре, исследованной в работе [14]. На поверхности золота ( 8 _m = -24,06 + 1,52 i при X ₀ = 800 нм) находится брэгговская решётка из диоксида кремния ( 8 _gr = 1,49²) высотой h gr = 100 нм. Параметры l 1 = 150 нм, l 2 =205 нм соответствуют одному из множества решений (1) при m =0 (значение m будем называть порядком брэгговской решётки). На рис. 2 представлены зависимости коэффициентов отражения и пропускания от числа периодов для описанной брэгговской решётки, для «высокой» брэгговской решётки с h gr =8 l 1 = 1200 нм, а также для брэгговского зеркала (слоистой структуры), рассчитанного для случая нормального падения плоской волны.

Отметим, что эффективность брэгговской решётки c h gr = 100 нм для ППП невысока. Например, для решётки с числом периодов N = 15 коэффициент отражения составляет R = 0,51, пропускания – T = 0,07, а

оставшаяся доля энергии падающей волны L = 0,42 приходится на паразитное рассеяние и поглощение в металле. Увеличение высоты решётки до 1200 нм (рис. 2) позволяет значительно (до 76%) увеличить отражение и сократить потери до 23,5%. Однако из-за технологических ограничений на аспектное отношение (отношение высоты ступенек решётки к их ширине) практическая реализация структур с такой высотой затруднена. В связи с этим представляет интерес снижение потерь на паразитное рассеяние без значительного увеличения высоты структуры. При дальнейшем рассмотрении различных примеров брэгговских решёток ограничим их аспектное отношение значением 3, реалистичным с точки зрения экспериментальной реализации.

Отражение R, пропускание Т

0      5    10   15   20   25   30 35

Число периодов

Рис. 2. Отражение и пропускание брэгговских решёток для ППП с hgr=100 нм (пример, аналогичный работе [10]) и hgr=1200 нм, а также брэгговского зеркала для плоской волны при нормальном падении в зависимости от числа периодов

2. Подавление паразитного рассеяния ППП

Рассмотрим метод подавления рассеяния, основанный на изменении конфигурации ступеньки, а именно, на переходе от однослойной ступеньки с диэлектрической проницаемостью 8 _gr и высотой h_gr на двухслойную ступеньку с диэлектрическими прони-цаемостями слоёв 8 ₁ и 8 ₂ ( 8 ₁< 8 ₂) и толщинами слоев h 1 и h 2 (рис. 3).

Предполагая, что толщина верхнего слоя h 2 (рис. 3) достаточно велика, константу распространения плазмонной моды в области такой ступеньки можно определить из (3), заменив в ней 8 _gr на 8 ₁, а 8 d на 8 2 (такую же процедуру следует провести с высотами и параметрами y j ). Тогда при фиксированных параметрах материала толщину h 1 можно определить аналитически из (3) и условия Re( Y 2 ) = Re( K d ), где к d = V k ₂ ² - k ₀ ² 8 _d . Данное условие соответствует частичному согласованию поперечных профилей поля плазмонных мод в ступеньке и вне её [11]. Так, в случае ступеньки с диэлектрическими проницаемостями 8 ₁ = 1,3² и 8 2 = 1,49 2 , расположенной на поверхности золота с 8 _m =-24,06 + 1,52 i , теоретическое значение толщины первого слоя ступеньки составляет h 1 =51 нм. Однако теоретическое значение h 1 может

оказаться неоптимальным с точки зрения подавления рассеяния, поскольку некоторая часть энергии ППП переносится за пределами области h 1 <  z <  h 1 + h 2 . Поэтому на основе численного моделирования проводилась дополнительная оптимизация толщины h 1 .

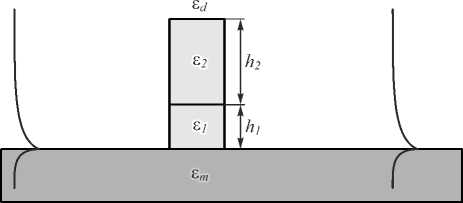
Рис. 3. Конфигурация ступеньки брэгговской решётки с подавлением паразитного рассеяния

Моделирование дифракции ППП на брэгговской решётке проводилось с помощью собственного программного обеспечения, разработанного в среде MATLAB и реализующего вариант метода связанных волн, также называемого методом фурье-мод (англ. rigorous coupled-wave analysis , Fourier modal method ) [15], адаптированный для решения задач интегральной оптики [16]. Для моделирования структур интегральной оптики исследуемая структура искусственно периодизуется, а на границы периода добавляются специальные «идеально согласованные» поглощающие слои (англ. Perfectly matched layers , PML), позволяющие устранить взаимодействие между периодами [16]. Программное обеспечение было предварительно протестировано с помощью коммерческих пакетов GSolver (также реализует метод фурье-мод) и COMSOL Multiphysics (реализует метод конечных элементов). Отличие интенсивностей дифракционных порядков, рассчитанных с помощью авторского программного обеспечения и пакета COMSOL, не превышает 0,005, различия с пакетом GSolver на несколько порядков меньше. Ранее с использованием данного программного обеспечения авторами было рассчитано и исследовано большое количество различных дифракционных структур, в частности, структуры для формирования интерференционных картин поверхностных плаз-мон-поляритонов [17–18], при этом результаты моделирования находились в соответствии как с результатами теоретического анализа, так и с экспериментальными результатами.

3.    Брэгговские решётки нулевого порядка

Рассмотрим брэгговские решётки нулевого порядка ( m =0). Ширины ступенек и областей между ними были получены из (6). Высота решёток выбиралась с учётом аспектного отношения, равного 3. В табл. 1 приведены параметры брэгговских решёток для ППП без подавления паразитного рассеяния ( h 1 =0) и с подавлением рассеяния (двухслойная ступенька, h 1 ≠ 0).

Параметры и рабочие характеристики исследуемых решёток, состоящих из 15 периодов, приведены в табл. 1.

Табл. 1. Основные параметры брэгговской решётки (m=0)

Тип ступеньки Параметры	Однослойная	Двухслойная ( h 1 =51 нм)
d , нм	324	329
l 1, нм	128	133
l 2, нм	196	196
hgr , нм	384	384
R	0,652	0,690
L	0,339	0,304

На рис. 4 а приведены зависимости отражения и пропускания от числа периодов брэгговской решётки. Из рис. 4 а и табл. 1 можно сделать вывод, что эффективность брэгговской решётки нулевого порядка относительно невелика. Переход к двухслойной ступеньке решётки незначительно (примерно на 3,5%) снижает паразитное рассеяние. На рис. 4 б представлены спектральные характеристики рассматриваемых решёток при числе периодов N = 15. На рис. 4 б вертикальными линиями показаны границы запрещённой зоны слоистой структуры для случая падения плоской волны с волновым вектором, соответствующим волновому вектору ППП. Несовпадение границ запрещённых зон слоистой структуры и брэгговской решётки для ППП связано с существенными потерями на паразитное рассеяние. В этом случае задача дифракции ППП на ступеньке (и планарной брэгговской решётке) значительно отличается от задачи дифракции плоской волны на плоскопараллельной пластинке (и слоистом брэгговском зеркале). В связи с этим формулы (1), (5), (6), использованные для расчёта брэгговских решёток для ППП, носят лишь приближённый характер.

4.    Брэгговские решётки первого порядка

Увеличения эффективности брэгговской решётки можно добиться, используя брэгговскую решётку первого порядка ( m = 1). Следует отметить, что само по себе использование решётки первого порядка при сохранении той же высоты, что и у решётки нулевого порядка, к увеличению эффективности не приводит, и даже наоборот, снижает эффективность. Как было показано выше (рис. 2), большое влияние на эффективность оказывает высота ступеньки. При фиксированном значении аспектного отношения для решётки первого порядка можно выбрать высоту, в три раза превышающую высоту решётки нулевого порядка, так как из (6) следует, что ширина ступеньки больше в три раза, чем у решётки нулевого порядка ( m =0). Таким образом, брэгговская решетка первого порядка позволяет «обойти» технологическое ограничение в виде аспектного отношения. Параметры и рабочие характеристики рассчитанных брэгговских решёток первого порядка приведены в табл. 2.

На рис. 5а приведены зависимости отражения и пропускания от числа периодов брэгговской решётки. Сравнение рис. 4а и рис. 5а показывает, что переход к решётке первого порядка увеличивает эффективность на 15,2%. Из табл. 2 можно также сделать вывод, что переход к двухслойной конфигурации ступеньки в брэгговской решётке первого порядка увеличивает эффективность ещё на 10,1 %, уменьшая по- тери на такую же величину. На рис. 5б представлены спектральные характеристики рассматриваемых решёток при числе периодов N = 15. В этом случае границы запрещённых зон для слоистой структуры и брэгговской решётки практически совпадают.

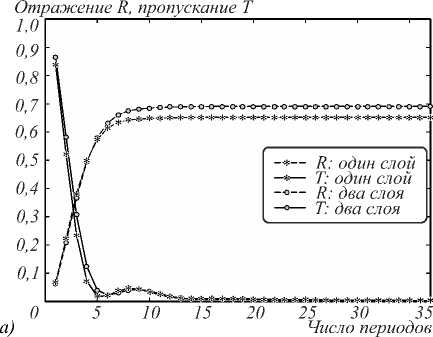
Рис. 4. Отражение и пропускание брэгговских решёток нулевого порядка с подавлением рассеяния и без него: зависимость от числа периодов (а); зависимость от длины волны при числе периодов N=15 (б).

Вертикальные линии – границы запрещённой зоны

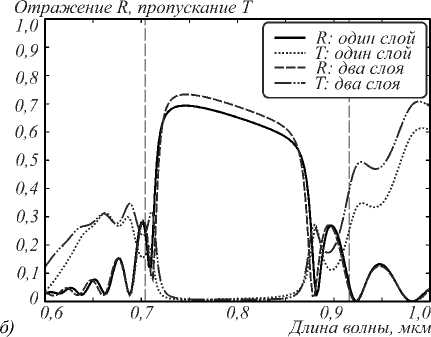
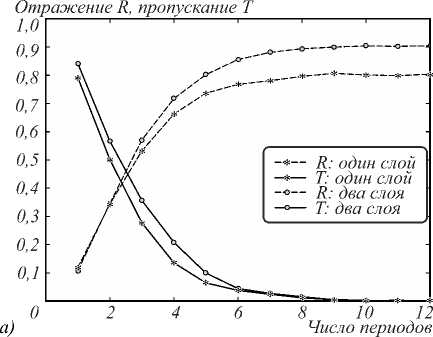
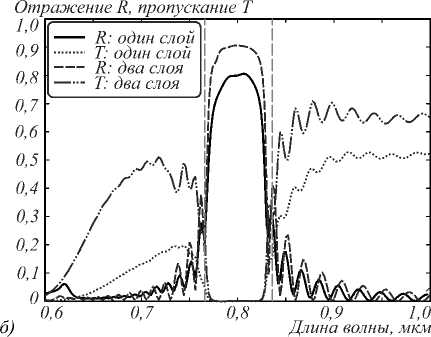
Рис. 5. Отражение и пропускание для брэгговских решёток первого порядка с подавлением рассеяния и без него: зависимость от числа периодов (а), зависимость от длины волны при числе периодов N=15 (б).

Вертикальные линии – границы запрещённой зоны

Табл. 2. Основные параметры брэгговской решётки (m=1)

Тип ступеньки Параметры	Однослойная	Двухслойная ( h 1 =95 нм)
d , нм	971	990
l 1, нм	384	403
l 2, нм	587	587
hgr , нм	1151	1151
R	0,804	0,905
L	0,196	0,095

5.    Сравнение результатов

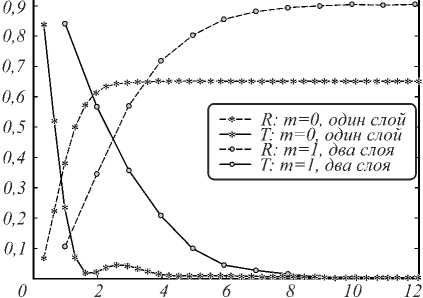
Для сравнения результатов объединим на одном рисунке (рис. 6) графики примеров с подавлением рассеяния для брэгговских решёток нулевого и первого порядков с аспектным отношением 3. Для оценки размеров структуры по оси абсцисс отложим не число периодов, а длину решётки. Отметим, что при фиксированном числе периодов размеры решётки первого по- рядка в три раза превышают размеры решётки нулевого порядка. Двухслойная брэгговская решётка первого порядка обеспечивает отражение на 25,3% большее, чем однослойная решётка нулевого порядка. Оценка спектров (рис. 4б и рис. 5б) показывает, что запрещённая зона (область с наибольшим отражением) уменьшается также примерно в три раза по длине волны при переходе от нулевого порядка решётки к первому.

Рассмотрим теперь эффективность работы предложенных методов для брэгговских решёток, параметры которых рассчитаны для других значений центральных длин волн, лежащих в интервале [0,7÷1,5] мкм. Результаты работы методов подавления рассеяния для различных длин волн приведены на рис. 7. Из рис. 7 можно сделать вывод, что для всех центральных длин волн в выбранном диапазоне использование предложенных методов подавления рассеяния существенно (от 15 до 35%) увеличивает эффективность брэгговской решётки.

Отражение R, пропускание Т

1.0 ----------1

Длина структуры, мкм

Рис. 6. Отражение и пропускание для брэгговских

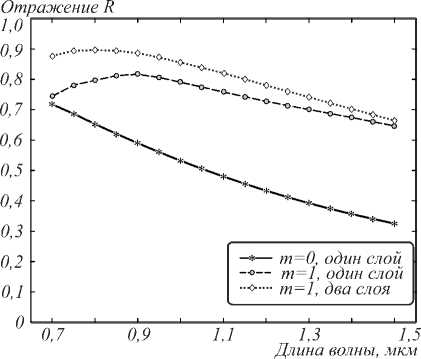
Рис. 7. Отражение для брэгговских решёток нулевого и первого порядков, рассчитанных для различных центральных длин волн в интервале [0,7÷1,5] мкм

решёток нулевого и первого порядков с аспектным отношением 3

Заключение

В работе приведено описание двух подходов к подавлению рассеяния ППП на брэгговских решётках: использование брэгговской решётки первого порядка и переход к двухслойной конфигурации ступеньки брэгговской решётки.

На примере брэгговской решётки, рассчитанной для центральной длины волны 800 нм, показано, что переход от решётки нулевого порядка к решётке первого порядка позволяет увеличить эффективность на 15,2%, а переход к двухслойной решетке первого порядка увеличивает эффективность ещё на 10,1 %.

Были также исследованы брэгговские решётки, рассчитанные для различных центральных длин волн, лежащих в интервале [0,7÷1,5] мкм. Показано, что для этих решёток с использованием предложенных методов подавления рассеяния можно увеличить эффективность на 15–35%.

Результаты работы могут найти применение при расчёте и создании высокоэффективных элементов плазмонной оптики.

Работа выполнена при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части «разработка и реализация моделирующего программного обеспечения», гранта Президента НШ-6307.2018.8 в части сравнения результатов и гранта РФФИ (проект №17-47-630323) в части «расчёт и моделирование брэгговских решёток для ППП».