Брэгговский волновод прямоугольного сечения

Волоконно-оптические волноводы служат передаточной средой для оптических систем связи и передачи информации. В течение нескольких последних десятилетий наблюдается неуклонное совершенствование как теории волноводов [1–4], так и технологий их изготовления со значительным улучшением технических характеристик. Вместе с тем расширяется и область их применения [5–8].

Кроме передачи оптического сигнала на расстояние, волноводы осуществляют функции элементов интегральных оптоэлектронных схем [1,2]. Структура такого волновода имеет характер плоско-параллельной слоистой среды. В нём световая волна распространяется в пределах плоскости, то есть в двумерном пространстве. Плоский волновод называют также планарным. Математическая модель распространения электромагнитной волны в такой структуре определяется точным расчётом с применением различных методов [9]. Более сильная локализация направленной оптической энергии имеет место в каналирующих волноводах, где электромагнитная волна распространяется в единственном выделенном направлении. Такие оптические структуры могут иметь поперечное выделенному направлению сечение круглой, эллиптической или прямоугольной формы. Волновод имеет среднюю часть (сердцевину), ближайшую к оси симметрии, и слой такой же формы, охватывающий сердцевину (оболочка). Различают полые волноводы с металлической оболочкой и диэлектрические волноводы, где сердцевина изготовлена из материала, более оптически плотного, чем материал оболочки. В последней структуре направление света в оптическом волокне осуществляется посредством эффекта полного внутреннего отражения на его границах. Возможно направление света в соответствии с правилом антирезонанса в интерференции света, отражённого от ближней и дальней к оси волновода границах оболочки. Это правило действует более эффективно, если оболочка многослойная, имеющая структуру одномерного фотонного кристалла. В этом случае сильное затухание поля в оболочке соответствует зонам в частотном спектре, называемым запрещёнными.

Полый волновод с запирающей многослойной оболочкой передаёт оптический сигнал с минимальными искажениями. Подобные структуры относятся к классу брэгговских волноводов [10, 11]. Это даёт возможность передавать на расстояние мощные сигналы в отсутствие дисперсии, без разогрева и деформации материала волновода, приводящих к дополнительным искажениям. Для диэлектрических волноводов искажения более существенны. Это позволяет определить брэгговский волновод как более перспективный, по сравнению с диэлектрическим, для передачи мощных сигналов без искажения. С точки зрения технологии направления света брэгговский волновод есть дефект в фотонном кристалле (вакуумный слой), по которому и направляется оптический сигнал.

Рассмотренные в настоящей статье прямоугольные волноводы имеют много приложений [12, 13]. Традиционно математическую задачу расчёта электромагнитного поля в прямоугольном брэгговском волноводе разделяют на две части: определение модового состава прямоугольного волновода и определение дисперсионной картины одномерного фотонного кристалла. Первая задача приближённо решается методом Маркатили [14, 15, 3, 4], использующем разделение переменных. Это возможно, поскольку в случае планарного волновода можно получить точное решение уравнений Максвелла [3,4]. Бесконечный периодический фотонный кристалл можно исследовать посредством «сшивания» решений на границах слоёв, используя понятие передаточной матрицы [16]. Ограничение фотонного кристалла в направлении, перпендикулярном слоям, требует разложения диэлек- трической проницаемости и функции, определяющей компоненты электромагнитного поля, в ряд Фурье. Результат в этом случае является приближённым и может быть рассчитан только численными методами.

В настоящей статье предложен метод расчёта поля электромагнитной волны в одномерном фотонном кристалле любого состава и размера (числа слоёв). В этом смысле брэгговский волновод может быть непосредственно исследован как фотонный кристалл с дефектом, где одномерный фотонный кристалл – это оболочка волновода, а полый волноведущий канал можно представить отсутствием некоторого количества слоёв, то есть дефектом кристалла. Метод использует разделение переменных. Его суть – правило, которое позволяет записать константы интегрирования уравнений Максвелла на всех границах раздела слоёв в кристалле. При этом нет необходимости «сшивать» решения уравнений, так как непрерывность тангенциальных компонент поля является свойством общего решения. Результат расчёта соответствует экспериментальным данным и теоретическим выводам, полученным в более ранней литературе.

1. Теоретическое решение задачи

Для расчёта распределения электромагнитного поля волны в волноводе обычно решаются уравнения Максвелла в однородных областях, а затем проводится «сшивание» решений на границах раздела однородных сред. Можно поступить иначе – решать уравнения Максвелла в общем виде для кусочно-неоднородной среды и получить результат, справедливый сразу для всех однородных областей. Являясь решением уравнений Максвелла, такая функция компонент поля будет заведомо удовлетворять закону непрерывности тангенциальных компонент полей на границах раздела сред.

Условимся полагать, что декартова система координат ориентирована следующим образом: ось OZ является осью симметрии прямоугольного волновода, плоскость XOY перпендикулярна оси симметрии, оси OX и OY параллельны границам раздела сердцевины, оболочки и всех её слоёв, как показано на рис. 1.

A H + [grad ^EX rot H ] + H e^ = 0, £                C c

где H - напряжённость магнитного поля, £ ( x , y , z ) -диэлектрическая проницаемость кусочно-однородной среды, to - частота волны.

Записанное для x -компоненты векторов уравнение

(1) имеет вид:

1 d£ d H_x 1 d£ d H

A H_x ---------- +

£ 8 y d y    £ d z d z

^^^^^^в

1 d£ d H y  1 d£ d H_z

+1

£ d y d x    £ d z d x

^-£ k 02 H x ,

где

» 2

2 = k 0 c ²

.

Заметим, что для всех компонент поля справедливы равенства дифференцирования:

1 I 8 ² H i - 1 d£ d H i'    £ d ^; 1 S H

H i ( d x i £ d x i d x i J H i d x i ( £ d x i

8 f 1 8HA  ₂ ( 1 d H^

= £-----I--I + £ I--I , dxi ( Hi £ dxi J     ( Hi £ dxi J ki = kx, ky, kz, xi = x, y, z, Hi = Hx, Hy, Hz.

Представим квадрат волнового вектора в виде суммы квадратов его компонент:

£ k ₀² = k. ² + k ² + k _².

xyz

Рис. 1. Схема брэгговского волновода

Так как диэлектрическая проницаемость кусочнооднородной среды определяется функцией Хэвисай-да, а решение волнового уравнения должно непрерывно зависеть от пространственных координат, будем решать дифференциальное уравнение методом разделения переменных.

Удобно ввести тригонометрические функции фазы волны во всех трёх координатных направлениях, положим

1 d Hy

£ H y 8 x

1 8 H_z

£ H_z 8 x

- k_z tan ( a ( x , e ) ) ,

1 8 H_x = 1 8 H_z

£ H_x 8 y £ H_z 8 y

- k z tan ( b ( y , e ) ) ,

С целью получения общего решения уравнений Максвелла запишем волновое уравнение, выведенное из системы уравнений Максвелла исключением неизвестных функций-векторов диэлектрической и магнитной индукции, а также напряженности электрического поля.

1 8 H_x = 1 8 H y = 1 8 H_z

H_x 8 z H_y 8 z H z 8 z

1 d H_x x

£ H_x 8 k_zx

= cot ( a ( x , e ) )

1 d H y

£ H_y 8 k_zy

= cot ( b ( y , e ) ) .

Новые введённые функции a ( x , £ ) и b (y , £ ) назовем фазой в направлении изменения координат x и y соот-

ветственно. Эти функции зависят от координаты, изменяющейся вдоль выбранной оси, и от значения диэлектрической проницаемости в области, содержащей эту координату.

Подставим определённые равенствами (4) функции в уравнение (2), учтём правило дифференцирования (3) и получим результат:

s dk z cx^al + s ² ( k z cot( a ) ) ² -s d k t^ b) +

+s ² ( k_z tan ( b ) ) ² +1| k_z tan( a ) + d y k_z tan ( a ) = (5) = -s k 02 + k_z 2 .

Интегрируя равенства (8) в однородной области 1, где s = s i , а поперечные компоненты волнового вектора равны k i 1 , приходим к следующим уравнениям:

s1 k,      _z x

----tan ( g ,) = tan ( k^Xj + const).                    (9) k i 1

Вычисляя интегралы (9), но для области 2, определим решения, относящиеся к обеим областям. Положим, что начало координат выбрано в области 1 на равных расстояниях от её параллельных друг другу границ:

Так как волновой вектор и диэлектрическая проницаемость постоянны в однородных областях, то внутри однородных областей уравнение (5) делится на два уравнения, если применить метод разделения переменных. На границах сред с изменением значений волнового вектора и диэлектрической проницаемости эти уравнения преобразуются, поскольку некоторые константы в них меняют значение при переходе из одной однородной области в другую. Преобразование уравнений определяет изменение функций фазы на границах однородных сред. Применяя метод разделения переменных, представим уравнение (5) в виде суммы двух уравнений и потребуем, чтобы оба они выполнялись. Оба уравнения преобразуются на границах раздела однородных областей кусочно-однородной среды. Уравнения имеют вид:

d k z cot ( a )     2_H . .x 2 ds . .

s-----------+ s (kz cot (a)) +--kz tan (a) + dx         x '    dz

5s,.          ,2

+--kz tan( a) = - kx, dy

-s d k z tenC b ) +s 2 ( k z tan( _b ) ) ² = _ k _y\             (7)

Рассмотрим эти уравнения. В первую очередь, опишем распространение электромагнитной волны в направлении оси OX брэгговского волновода (рис. 1). Для такого случая верно то, что волна отражается от границ однородных областей, перпендикулярных оси OX , и пересекает их. Область, в которой выбрано начало координат, назовём областью 1. Окружающую её однородную область брэгговского волновода – областью 2. Третий слой оболочки – область 3 и т.д.

В однородной области 1 эти уравнения для всех компонент поля можно преобразовать к виду:

I k d arctan s — tan (g,)

I

d x i

= k i ,

k z tan( g i )

k z cot( g i )

k i = k x , k y , g i = a , g 2 = b .

k i i

—¹ tan ( k_i1 x i + const), x i <  d i 1 ,

= < si ki2

-2- tan( k i 2 x i + const), x i >  d i 1 ,

_ s ₂

5 ( x i - d i 1 ), | x i | = d i 1 ,

1 c- cot ( k i 1 x i + const), | x i | <  d i 1 , s i

■^i ² cot ( k i 2 x i + const), I x i I >  d i 1 ,

_s 2

где d ik = d xk , d vk – ширина k -й однородной области в направлениях осей координат ( k > 1), ширина первой однородной области – 2 d i 1 .

Заметим, что уравнения (10), (11) содержат 5 -функцию, принимающую на границе областей бесконечно большое значение. Учитывая это замечание, имеем на границе значение тангенса функции фазы в перпендикулярном границе направлении, равное бесконечности, соответственно, значение функции фазы g i , равное п . Поскольку изменение функции фазы включает в себя оптический путь внутри однородной области и изменение фазы при отражении, то условие равенства фазы п является условием распространения волны вдоль оси волновода.

Найдём производную функции a. С этой целью продифференцируем уравнение (6) в однородной области. Выражая из полученного равенства d a /d x , получаем:

d a d x

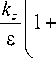
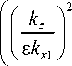
- 1 cos( a )² .

Зная производную d a /d x , можно заменить переменную интегрирования в уравнении, определяющем x -компоненту напряженности магнитного поля:

H_x ( x , y , z ) = H ₀ ( y , z ) exp

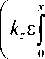
tan ( a ( x ' ) ) d x ‘

Выполняя интегрирование, получаем:

H x ( x , y , z ) = H 0 ( y , z ) sin ( a ( x )) x

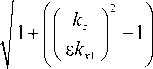
cos ( a ( x ))²

Аналогичные вычисления можно применить к волне, распространяющейся вдоль оси OY . Здесь необходимо использовать уравнение (7). Окончательный результат в области, содержащей начало координат, имеет вид:

H x ( x , y , z ) = H 0 sin ( a ( x )) cos ( b ( y )) exp ( k z z ) x

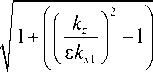
cos ( a (0))²

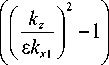
cos ( a ( x ))²

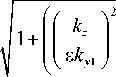
A

- 1 cos ( b (0))²

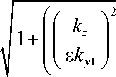
A

- 1 cos ( b ( y ))²

Введём обозначение для множителя A ( x ) , возникающего в решении при пересечении границы i -й (по порядку счёта в направлении оси X ) области от начала координат:

A(^x ) =

1 +

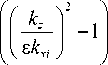
cos( a ( d , ■_₁ ))^:

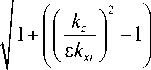
cos ( a ( x ))²

где d i – длина i -й области по оси X .

Тогда пройденный при пересечении предыдущих областей оптический путь волны соответствует решению вида:

-1

Hx (x, y, z) = Hо (y, z) sin (a (x)) A (x )П A (dn) = n=1

= H0 (y, z) sin (a (x)) A (x) , где введены обозначения:

-1.

A ( x ) = A, ( x ) П A ( d n ), du <  x <  d i , n =1

d – длина -й области по оси X .

Окончательный результат для волны, распространяющейся во всех областях, рассчитывая в направлении от начала координат, и прошедшей в -ю область, отсчитывая в направлении оси X, и в j-ю – в направлении Y, имеет вид:

Hx (x, y, z) = Hоx sin (a (x)) x x cos (b (y)) exp (kzz) A (x)) B (y), Hy (x, y, z) = Hо y cos (a (x)) x x sin (b (y)) exp (kzz) A (x)) B (y), Hz (x, y, z) = H0z cos (a (x)) x x cos (b (y)) exp (kzz) A (x)) B (y), здесь

B , ( y ) =

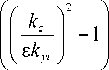
cos( b ( 5 , -))²

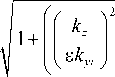
A

- 1 cos( b ( y ))²

j -1

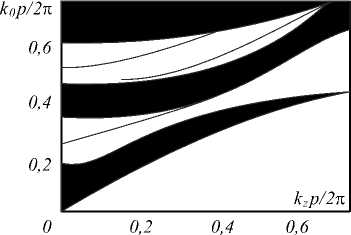
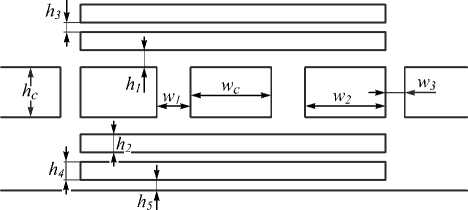
B(y) = Bj(y)ПB(5n), 5j--1

где 5j - длина j-й области, отсчитывая от начала координат в направлении оси Y.

Электромагнитная волна удовлетворяет шести уравнениям Максвелла, записанным для компонентов поля [4]:

цю ,_   dEi  дE_k    srn „ дHi  дH_k

Hi —            ,       Ei —             , c       дxk   дxj      c дxk   дxj

E,= Ex, Ey, Ez, x, = x, y, z, H = Hx, Hy, Hz.

Уравнения, аналогичные уравнению (2), описывающему x-компоненту поля, записанные для всех компонент магнитного поля, полностью их определяют. Для описания электрического поля необходимы ещё три уравнения:

ею   дH дH_k

E i — c       дxk дx_j

Поскольку уравнение (2) решено в общем виде, результирующие функции тангенциальных к границе раздела сред компонент поля должны быть непрерывными при переходе из одной среды в другую. Нормальные компоненты электрического поля должны испытывать разрыв и относиться непосредственно по обе стороны границы сред как диэлектрические проницаемости сред.

Функция в решении для магнитного поля, зависящая от координаты x, представима равенством:

( x .A cos( a (x)) xA (x) = exp I kz sj tan (a (x)) dx I. (17) I 0

Согласно (17) эта функция непрерывна во всех областях кусочно-однородной среды и на их грани- цах. Рассматривая также остальные функции в решении (13)–(15), приходим к выводу: на границах волновода все компоненты магнитного поля сохраняют своё значение. Рассмотрим поведение компонент электрического поля на границе раздела сред, перпендикулярной оси OX s®    dHz 8Hy

Ex —---.

c       8y 8z

Рассмотрим поперечную магнитную волну, у которой равна нулю z-компонента магнитного поля. Тангенциальная компонента магнитного поля Hy непрерывна вместе с z-производной. Следовательно, нормальная к границе раздела сред компонента электрического поля Ex изменяет при смене сред своё значение в отношении диэлектрических проницаемостей соответствующих сред.

X- и y-производные компонент магнитного поля, описываемых уравнениями (13)–(15), испытывают разрыв с соотношением граничных значений в отношении диэлектрических проницаемостей, поэтому в уравнении s®    8Hy 8Hx

--Ez —--- c       8x    8y z-компонента электрического поля, тангенциальная границе раздела сред, непрерывна на ней.

Рассмотрим далее поперечную электрическую волну с нулевой z-компонентой электрического поля:

s®    8H_x8Hy

--Ez —---— 0

c      8xy 8xx

В этом случае выполняется равенство:

8Hy 8Hx lx-—.

Продифференцировав уравнения (16), определяющие x- и y-компоненты электрического поля, а также полагая, что приращение координаты y на границе раздела сред, перпендикулярной оси OX, равной нулю, с учётом (18) приходим к уравнению:

d (s®  )_8²Hz  8²Hz  d²Hx  8² Hy

I     Ex I —+— 0 . (19)

8x ( c   )  8x 8y   8x 8y   8z 8y   8z 8x

Равенства (19) показывают, что выражение ((s®/c)E_x) не изменяется при переходе границы, перпендикулярной оси OX. Следовательно, нормальная к границе раздела сред компонента электрического поля изменяется обратно пропорционально отношению диэлектрических проницаемостей однородных областей.

Таким образом, тангенциальные и нормальные компоненты электрического поля поперечных электрических и поперечных магнитных оптических волн удовлетворяют закономерностям, отражённым в урав- нениях Максвелла, если магнитное поле определяется равенствами (15).

2. Численный расчёт и обсуждение результатов

Выражение решения уравнений Максвелла через функции фазы в поперечных к оси волновода взаимно-перпендикулярных направлениях – a (x) и b (y), определённые уравнением (4), позволяет записать константы интегрирования дифференциальных уравнений Максвелла. Можно ввести универсальное правило записи констант интегрирования, сформулируем его. С этой целью рассмотрим функцию, определяющую дисперсионную зависимость решения (15) от координаты, в двух формах – содержащей функцию gi (xi) и содержащей непосредственно координату xi, для области, содержащей начало координат:

kzs, tan(gi (dn)) — k_n tan(k, dn).                  (20)

Индекс 1 относится к характеристикам волны в первой среде.

Далее запишем зависимость (20) для области (область 2), граничащей с областью, включающей в себя начало координат:

kz S2tan(g, ( dii)) — ki2tan(k_n di + C).             (21)

Из (20)–(21) определим первую константу интегрирования C на границе областей 1 и 2:

^S2 1

C — arctan--tan(k_iX d, J .

I Si k2          J

В области, третьей по счёту в направлении оси X от начала координат, решение (20) имеет форму:

kzS3 tan(gi (di2)) — k3 tan(k_ndi + Ci).             (22)

Таким образом, из (22) следует, что вторая константа C1 задаётся равенством:

(s₃k.-,

C1 — arctan I--² tan (ki₂di₂+

V^S2 ^ki3

^{( S}2 ki 1 . / 7 7 x ill

+ arctan--tan( kd,)    .

I Si ki2            JJI

Чтобы записать третью константу интегрирования, нужно применить правило, позволившее определить первые две константы. Суть этого правила: если известна константа в одной (произвольной по счёту) области - C, материальный состав (s_i) и геометрические размеры (длина d ) области, граничащей с выбранной, а также частота волны и диэлектрическая проницаемость рассматриваемой области (s), то константа в ней равна:

( s k, C — arctan--²tan (k,d + С)

Is, k ^{V 7}

где k и k1 – волновые векторы в двух граничащих областях. Решение можно записать как exp (-J kz s tan( a )dx) =

= exp(-J k tan( kx + C1)dx) = cos (kx + C1).

Таким способом легко записать решение для электромагнитной волны в слоистой кусочно-однородной среде любого состава и размера. Заметим, что выражение для напряжённости электрического и магнитного полей, а также дисперсионное соотношение может быть определено указанным способом не только для периодической бесконечной структуры, но и для апериодической конечной кусочно-однородной среды.

На рис. 1 изображена схема диэлектрического волновода прямоугольного сечения с произвольным составом сред, чередующихся в поперечных к оси волновода взаимно-перпендикулярных направлениях. Заметим, что предлагаемый в настоящей статье метод, как и другие алгоритмы решения рассматриваемой задачи [3,4], не учитывает угловые зоны. Поэтому на рис. 1 эти области волновода не обозначены цифрой.

Используя формулу (23), можно определить электромагнитное поле в такой структуре. В первую очередь, зададим условие полного внутреннего отражения на границах волновода. Необходимо, чтобы фаза волны за пределами волновода была комплексной величиной. При этом её мнимая часть должна стремиться к бесконечно большому положительному значению. Математически это условие имеет вид:

tan (a (d)) = i.

Рис. 2. Схематическое изображение волновода прямоугольного сечения

Для того, чтобы записать дисперсионное соотношение, необходимо сложить два уравнения, определяющие функцию фазы в поперечных направлениях:

tan ((2 px - h) kx + C ) = ^ k^i

^S1 kx 2

tan (-hk_x + C = ^S3 k i

⁽x ) Si kx3

^

^ tan (2 p_xk_x + пт) = i

s₂k_rS3 k_r

+ -3

^S1 kx 2 ^S1 kx 3

1 + ^S2 kx^S3 kx

^S1 kx 2 ^S1 kx 3

Здесь m =0, 1,2, ..., индексы 1, 2, 3 обозначают номер области на рис. 2, ширина волновода в направле- нии X равна px, x-компоненты волновых векторов в областях 1 и 2 волновода определяются равенствами:

Sik0 = kx + ky+kZ, kx22 = s2k0- ky- kZ , kx3 = S3 k02 - ky - kZ, C = const.

Второе дисперсионное уравнение для определения величин kx и ky записывается как соотношение функций фазы b (y):

tan((2py - hi)ky 1 + Cl) = tan (-hk,+ C = S5 ky1

Si ky3

^ tan (2 pyky + п n) = i

S4 ky₊S5 k^

^S1 ^ky 4 ^S1 ^ky 5 1 +S4 ky S5 ky

S1 ky 4 S1 ky 5

Здесь n =0, 1,2, ..., как и ранее, индексы 1, 4, 5 обозначают номер области на рис. 2, ширина волновода в направлении Y равна py, y-компоненты волновых векторов в областях 4 и 5 волновода определяются равенствами:

2  2222  222

ky4 = S4k0 - k_x - kz , ky5 = S5k0 - k_x - kz .

Решения с различными значениями целочисленных величин m и n определяют возможные моды, распространяющиеся в прямоугольном волноводе.

С помощью уравнений (23)–(25) можно рассчитать симметричный прямоугольный брэгговский волновод, схема которого показана на рис. 1.

Решения для симметричного по осям X и Y брэгговского волновода определяются двумя дисперсионными уравнениями, непосредственно следующими из уравнений (23)–(25). Дисперсионные уравнения для квадратного волновода совпадают с решением этой же задачи для брэгговского планарного волновода, так как решение предполагает разделение переменных с последующим сведением задачи к расчёту плоского волновода.

Таким образом, достоверность вычислений, приведённых выше, можно подтвердить сравнительным анализом диаграмм, построенных по двум различным формулам для планарного волновода – конечным выражениям традиционного решения и метода, представленного в настоящей статье. На рис. 3–4 показаны две фазовые диаграммы, одна из которых (рис. 4) приведена в работе [17], другая (рис. 3) – построена по формулам (23)–(25), первый волновод бесконечный, оболочка второго состоит из ста слоёв (50 периодов). Прочие параметры одинаковы: оболочка волновода является одномерным фотонным кристаллом с периодом 3p, кристалл содержит две компоненты – среды с показателями преломления n1 = 1 и n2 = √12; толщины слоёв, заполненных средами 1 и 2, составляют соответственно d1 = p /3 и d2 =2p /3 (р – период оболочки).

Сравнивая рис. 3 и 4, можно видеть, что положения и границы зон на них совпадают, что свидетельствует о достоверности представленного в настоящей статье метода расчёта дисперсионной диаграммы.

О 0,2       0,4      0,6

Рис. 3. Дисперсионная диаграмма бесконечного брэгговского волновода, рассчитанная в [17]

Рис. 4. Дисперсионная диаграмма 100-слойного двухкомпонентного брэгговского волновода, рассчитанная по формулам (7) – (9)

Далее проверим достоверность представленного в статье метода исследования дисперсионных свойств волновода и его модового состава на примере прямоугольного волновода. Используя подобный метод, можно, кроме определения дисперсионных характеристик мод, задавая значения длины волны излучения, материал компонентов и структуру волновода, рассчитать его геометрические параметры. Так, в работе [5] для первых трёх мод вычислены параметры волновода, поперечное сечение которого изображено на рис. 5. Материальные и геометрические (округлённые вычисленные) параметры структуры приведены в подписи к рис. 5 согласно обозначениям на изображении.

Для расчёта использовалось фазовое уравнение, выполнение которого является обязательным условием распространения электромагнитной волны в волноводе [5]:

4Re(к) d + 2Аф = 2nM , (26)

где 2d - размер волновода, Аф - изменение фазы электромагнитной волны при отражении от границы сердцевины, М – порядок резонанса, k – поперечная оси волновода и границам раздела сред компонента волнового вектора.

Рис. 5. Поперечное сечение волновода, состоящего из однородных областей, заполненных воздухом и плотным полиэтиленом (low-density polyethylene LDPE). Показатель преломления полиэтилена 1,54 – 0,00066845i [5].

Геометрические параметры:

wc = 1500 мкм, hc = 750 мкм, h1 = h3 = h5 = 63 мкм, h2 = h4 = 376 мкм, w1 = w3 = 190 мкм, w2 = 1130 мкм

При вычислении постоянной распространения волновода (компоненты волнового вектора) с прямоугольным сечением хорошее совпадение с результатом численного расчёта даёт метод эффективного показателя преломления [5]. Этот метод применяется с целью разделения переменных в волновом уравнении. Он сводит расчёт прямоугольного волновода к исследованию двух перпендикулярных друг другу плоских структур.

Если использовать для расчёта метод эффективного показателя преломления, то волновод представляется двумя плоскими структурами. Моды ТМ - и ТЕ-поляризации будут направлены в двух поперечных оси волновода и перпендикулярных друг другу направлениях. При расчётах в работе [5] эффективный показатель преломления для мод обеих поляризаций полагался равным neff = 0,98. Поперечный волновой вектор через эту величину выражается следующим образом:

k = код/1 — nf .

Вычисление данных, необходимых для подстановки в уравнение, проводилось частично численным методом (компонента волнового вектора), частично – аналитическим (Аф). Последний член уравнения определялся из соотношений для коэффициентов отражения электромагнитной волны от границ сердцевины [5].

В силу предлагаемого автором метода возможно осуществить вычисление Аф, руководствуясь следующими соображениями. Изменение функции фазы на пространственном отрезке вдоль осей включает в себя соответствующий оптический путь волны и изменение фазы при отражении от преград, расположенных на отрезке пути:

i 1 °2

g (d, J = arctan--tan(kdJ i                     I ki2 £i

Аф = к d +--.

i1i1 2

Сердцевина принимается первой областью, её ширина вдоль осей OX и OY – 2di1.

Складывая уравнения (26) и (27), получаем условие распространения волны в рассматриваемой структуре:

I k„ -,                   1

4arctan---tan(k^d, J = 2пМ .

I ki2 -1              J

Проведя несложные преобразования, приходим к эквивалентному уравнению:

(k„ s„ 1

Retan(2Re( k, J d_n + пM^F =

I ki2 Si J     '

( k.. S-A

= Imtanh (2 Im (k, [) d, [) F,

I ki2 Si J       '

F = [1 - tan (2 Re (ki1) di 1 + пM) tanh (2 Im (ki 1) di 1)], F₂=[1 + tan (2Re( ki 1) di1 + пM) tanh (2Im( ki 1) di 1)].

Аналогично вычисляется размер слоёв. Принимая во внимание, что для обеспечения антирезонанса значение изменения фазы между границами слоя необходимо положить равным п, запишем уравнение для определения толщины слоя:

( k. s 1

Re -О-j- tan(Re(kij)dj+п(M +1/2))F =

I kj+i -j J ^v

( k„ -1

= Im --tanh (Im (kij) dj) F2,

I k_u+i -j J ^x '

F = [1 - tan (Re (kij) dij +

+ п (M +1/ 2)) tanh (Im (kij) dj )],

F2 =[1 + tan (Re( kj) dj +

+ п (M +1/ 2)) tanh (Im (kj) dj )], где индекс j обозначает номера слоя и соответствующие ему материальные (-j) и геометрические (dj-ширина слоя) параметры.

Результаты расчёта для сердцевины волновода и слоёв, заполненных воздухом, приведены в табл. 1. Для сравнения в табл. 2 приведены те же данные, но рассчитанные в работе [5]. Численные результаты, представленные в двух таблицах, близки, что, как и ранее, свидетельствует о достоверности представленного в настоящей статье метода.

Значение эффективного показателя преломления было принято как данное. Зная геометрические параметры волновода, можно априори проверить принадлежность принятого значения разрешённым линиям на дисперсионной диаграмме. Расчёт показал, что значение 0,98 является решением дисперсионного уравнения для волновода, изображенного на рис. 4, следовательно, в волноводе с рассчитанными параметрами возможно возбуждение мод, соответствующих выбранным размерам, с длиной волны 1ТГц. Метод эффективного показателя преломления для вычисления постоянной распространения в волноводе, изображенном на рис. 4, применён и в настоящей работе. Здесь оригинальным является способ расчёта плоских слоистых структур. Решение дисперсионного уравнения, составленного с использованием уравнений (23)–(25), привело к следующему результату: потери квазиТЕ00 -моды рассматриваемого волновода составляют 0,045 дБ/см, потери квазиТМ00- моды – 0,27 дБ /см. Для сравнения, эти величины, рассчитанные в статье [5], равны 0,05 дБ /см и 0,3 дБ /см соответственно.

Табл. 1. Эффективный размер сердцевины и воздушного слоя оболочки волновода, изображенного на рис. 4

M	Размер сердцевины		М	Размер воздушного слоя оболочки
	ТЕ -поляризация	ТМ -поляризация		ТЕ -поляризация	ТМ -поляризация
1	1507,6	–	0	1130,7	–
2	2261,3	753,78	1	1884,4	376,89
3	3015,1	1507,6	2	2638,2	1130,7

Табл. 2. Эффективный размер сердцевины и воздушного слоя оболочки волновода, изображённого на рис. 4 [5]

M	Размер сердцевины		М	Размер воздушного слоя оболочки
	ТЕ -поляризация	ТМ -поляризация		ТЕ -поляризация	ТМ -поляризация
1	1507,50	–	0	1130,61	–
2	2261,27	753,80	1	1884,39	376,90
3	3015,05	1507,60	2	2638,16	1130,70

Выводы

Выведенный в статье метод расчёта волновода с прямоугольным сечением и многослойной оболочкой позволяет записать решение уравнений Максвелла для такой структуры при произвольном составе сред, заполняющих области вокруг волноведущего канала. В таком решении все тангенциальные компоненты электромагнитного поля на границах раздела сред непрерывны.

Метод не приводит к некоторым новым, ранее не использующимся при решении рассматриваемой задачи функциям, он лишь определяет константы интегрирования решений дифференциальных уравнений в любой области, однородно заполненной средой-компонентом, без использования процедуры «сшивания» этих решений.

Представленный метод имеет следующие преимущества: он позволяет с одинаковой сложностью и объёмом вычислений рассчитать характеристики как бесконечной, так и ограниченной слоистой структуры; увеличение числа компонент фотонного кристалла также не усложняет расчёт; сама процедура расчёта не предоставляет особых трудностей, она удобна для программной алгоритмизации.