Быстрая оценка энтропии длинных кодов с зависимыми разрядами на микроконтроллерах с малым потреблением и низкой разрядностью (обзор литературы по снижению размерности задачи)

Цифровая экономика должна базироваться на безопасных облачных сервисах обработки личных и корпоративных данных. Сегодня безопасность облачных сервисов строится на применении парольной аутентификации. К сожалению, человек не может запоминать длинные пароли из случайных символов для своей безопасной работы в интернет-облаках.

Для того чтобы избавить человека от необходимости запоминать длинный пароль доступа, в США, Канаде и странах Евросоюза пытаются применять так называемые «нечеткие экстракторы» [1–3]. Из-за того, что «нечеткие экстракторы» используют классические коды обнаружения и исправления ошибок с 20-кратной избыточностью, пароли, сцепленные с биометрией, оказываются короткими. Так, код пароля для папиллярного рисунка отпечатка пальца составляет примерно 16 бит, или 2 случайных символа в 8-битной кодировке. Очевидно, что вычисление энтропии пароля из двух случайных символов легко выполняется по Шеннону.

В России эта проблема решается использованием больших искусственных нейронных сетей, которые заранее обучаются преобразовывать биометрические данные человека в длинный код его пароля доступа. При этом обучение выполняется автоматически алгоритмом ГОСТа Р 52633.5-20111. За один бит кода пароля пользователя отвечает один нейрон нейросети, по этой причине нейросетевые преобразователи биометрии обычно строят под длину кода в 256 бит. Наиболее распространенные сегодня операционные системы Linux, Windows, Android воспринимают пароли длиной не больше 256 бит (32 случайных знака в 8-битной кодировке). Нейросетевые преобразователи биометрия-код выгодно строить под максимально возможную длину пароля доступа, характерную для той или иной операционной системы. По этой причине нейросетевую технологию защиты иногда называют «высоконадежной»2. Хакер, ничего не знающий о биометрическом образе пользователя «Свой», вынужден перебирать все состояния очень длинного кода доступа [4].

Как правило, после получения длинного личного ключа пользователя или его длинного пароля доступа запускается некоторый криптографический протокол выполнения аутентификации. Криптографические протоколы принято считать надежными, если энтропия блока шифротекста длинной в 256 бит будет составлять ровно 256 бит. Если энтропия оказывается больше или меньше, то криптосхема защиты информации может оказаться дефектной. Эти соображения с некоторой натяжкой можно перенести на защиту криптографического ключа «нечеткими экстракторами» или размещением его данных в параметрах обученной нейронной сети. Знание энтропии состояний кода ключа оказывается эффективным контрольным параметром при анализе уровня защиты от попыток его подбора.

В случае, если разрядность кода доступа мала, то расчет энтропии этих кодов можно выполнить по Шеннону. В частности, при кодах длиной 16 бит «нечеткого экстрактора» энтропию следует вычислять по следующей формуле [2; 3]:

H ( x 1 , x 2 ,..., x 1б ) = - ^ p- log₂( p ) , ⁽¹⁾ i = 1

где p_i – вероятность появления одного из 2¹⁶ = 65 536 состояний кодов.

Для того чтобы оценить вероятность появления 216 состояний кода, необходимо иметь базу из 216+4 папиллярных рисунков отпечатков пальцев «Чужой». Собрать базу из почти миллиона рисунков отпечатков пальцев сложно, но технически возможно. По этой причине процедуры вычисления энтропии по Шеннону для «нечетких экстракторов» вполне применимы.

Положение коренным образом меняется, если мы переходим к кодам длинной в 256 бит:

H ( x i , x 2 ,..., x 256 ) = — £ p_s ■ log 2 ⁽ p ^. ⁽²⁾ = 1

Для прямых оценок очень малых вероятностей появления 2256 состояний кода потребуется использовать базу из 2256+4 биометрических образов «Чужой». Технически невозможно создать и использовать столь большую тестовую базу.

Обзор литературы

Для решения проблемы больших тестовых баз и сложных вычислений энтропии по Шеннону в России разра- ботан стандарт ГОСТ Р 52633.53. По рекомендациям этого стандарта требуется применение малых тестовых баз образов «Чужой» объемом от 21 до 64 примеров.

Применение стандарта дает экспоненциальное снижение объема тестовой выборки. Этот выигрыш обусловлен тем, что стандарт рекомендует переходить от анализа обычных кодов в пространство расстояний Хэмминга:

c

256 i h = E ® i=1 „ н

_ x_t

где '' c i '' – дискретное состояние i -го разряда кода «Свой»; '' x i '' – дискретное состояние i -го разряда случайного кода образа «Чужой»; ⊕ – операция сложения по модулю 2. Если пространство обычных 256-битных кодов имеет огромное число состояний, то пространство расстояний Хэмминга будет иметь всего 257 состояний, наблюдается экспоненциальное снижение размерности задачи.

По малой выборке от 21 до 64 опытов можем вычислить математическое ожидание E ( h ) и стандартное отклонение σ ( h ). Знание о значениях этих двух статистических моментов позволяет оценить вероятность угадывания кода «Свой» P ₂ . Оценка вероятности выполняется в рамках гипотезы нормальности:

P 2 -

1 су( h yj2n

(exo Г< E ( h *— u ' 1 ^ I 2 ( o ( h ) ) ²

i

—ro

—

• du . (4)

В этом случае энтропия нейросетевого преобразователя оценивается следующим образом:

H (" x 1 , x 2 ,..., x ₂₅₆ ") ~- log₂( P₂) . (5)

Применение тройки преобразований (3), (4), (5) позволяет уйти от экспоненциальной вычислительной сложности оценок энтропии длинных кодов по Шеннону4. Более того, эта совокупность вычислительных процедур обеспечивает линейную вычислительную сложность и снимает проблемы привлечения процессоров, поддерживающих 32- и 64-разрядные вычисления5 [5].

Кроме того, отпадает необходимость тратить значительные объемы памяти на хранение больших объемов тестовой базы образов «Чужой». Достаточно помнить порядка 30 тестовых образов «Чужой». Столь малое число образов «Чужой» может быть использовано как образы-родители. Их морфинг-скрещиванием могут быть получены сотни тысяч синтетических тестовых образов-потомков с помощью процедур, регламентируемых национальным стандартом ГОСТ Р 52633.2-20106. В одном поколении морфинг-скрещиванием удается увеличивать число естественных тестовых примеров «Чужой» примерно в 20 раз, соответственно, для получения больших тестовых баз приходится размножать данные в нескольких поколениях [6–9]. Процедуры размножения данных применимы и к примерам образа «Свой» в рамках бутстрап-идео-

• ³    ГОСТ Р 52633.5-2011. Защита информации...

• ⁴    Быстрые алгоритмы тестирования нейросетевых механизмов биометрико-криптографической защиты информации / А. Ю. Малыгин [и др.]. Пенза: Изд-во Пензенского государственного университета, 2006. 161 с. URL: (дата обращения: 29.04.2020).

• ⁵    Нейросетевая защита персональных биометрических данных / под ред. Ю. К. Язова. М.: Радиотехника, 2012. 157 с. URL: http://www.radiotec.ru/book/170 (дата обращения: 29.04.2020).

• ⁶    ГОСТ Р 52633.2-2010. Защита информации. Техника защиты информации. Требования к формированию синтетических биометрических образов, предназначенных для тестирования средств высоконадежной биометрической аутентификации.

логии, заполнения пустых интервалов реальных гистограмм распределения7.

К сожалению, применение морфинг-размножения биометрических образов в нескольких поколениях приводит к их вырождению. В частности, возникают дефекты «кошмара Дженки-на» [10–12] и дефекты вырождения корреляционных матриц8. Крайне важным является то, что, применяя специальное программное обеспечение, удается практически полностью устранить дефекты размножения данных в первых нескольких поколениях9.

Материалы и методы

Еще одним направлением работ, связанных с упрощением вычислений, является симметризация корреляционных связей в длинном коде с зависимыми разрядами. Идея метода сводится к замене изначально асимметричной корреляционной матрицы на ее симметричный аналог:

где параметр симметричной матрицы r^; вычисляется простым усреднением модулей всех коэффициентов корреляции исходной асимметричной матрицы:

r" ” E(|r I)

n2 - 2 n

0, 5 n ² - n

∑ r i . (7)

= 1

¹      r l       r 2

r l       ¹       r n + 1

r 2     r n + 1       ¹

. r n    r 2 n - 2    r 3 n - 3

r r

^

^v      ^      ■ r   r   1

^v

r

rn r2 n-2

r 3 n - 3

^v r

^v r

^v r

^

При росте размерностей задачи (число нейронов в нейросети: 32, 64, 128, 256) ошибка приближения (7) быстро падает. По этой причине оценивать энтропию можно через вычисления показателя средней коррелиро-ванности (7) [13; 14]. Результаты в этом направлении исследований отражены в работах [15–18].

Очевидно, что при рассматриваемых классах преобразований крайне важным является то, насколько быстро сходятся вычислительные процессы и как быстро снижаются ошибки приближений. Эти вопросы рассматриваются в работах [19–22].

Первоначально задача вычисления энтропии длинных кодов с зависимыми разрядами рассматривалась как некоторая достаточно быстрая и эффективная процедура тестирования. Однако в 2009 г. с привлечением рассматриваемых в данной статье процедур была итерационно решена обратная задача нейросетевой биометрии. Через быстрое вычисление энтропии удалось извлечь знания из нейросети. Это послужило началом работ, улучшающих процедуры вычисления энтропии в контексте решения обратных задач нейросетевой биометрии [23–26].

• ⁷    Качалин С. В., Иванов А. И. Заполнение пробелов биометрических данных генетическим алгоритмом размножения реальных примеров образа «Свой» без использования «мутаций» // Компьютерные науки и информационные технологии: материалы Международной науч. конф. (30 июня–03 июля 2014 г.). Саратов: Изд-во «Наука», 2014. С. 154–157.

• ⁸    Туреев С. В., Малыгина Е. А., Солопов А. И. Методика формирования тестовых баз для проверки качества обучения нейросетевых преобразователей биометрия-код // Сборник научных статей по материалам I Всероссийской науч.-техн. конф. «Безопасность информационных технологий» (24 апреля 2019 г.). Пенза, 2019. С. 90–101.

• ⁹    Свидетельство о государственной регистрации программы для ЭВМ № 2019662112 «Саморазвивающийся эмбрион-архив тестовой базы биометрических образов «чужой» / А. В. Безяев [и др.]. Дата государственной регистрации: 17.09.2019.

Результаты исследования

Одной из проблем нейросетевой биометрии является необходимость использования малогабаритной физически и криптографически защищенной доверенной вычислительной среды [27]. Как правило, доверенную вычислительную среду приходится создавать с использованием малопотребляющих, низкоразрядных микроконтроллеров при ограниченном объеме памяти. Система биометрико-криптографической защиты оказывается надежной, только если все криптографические операции над данными и нейросетевые операции будут выполняться внутри доверенной малогабаритной вычислительной среды.

Последнее означает, что на малопотребляющих, низкоразрядных процессорах нужно уметь точно вычислять интегралы вероятности (4). Вычислить подобный интеграл на компьютерах с 32- или 64-разрядной арифметикой несложно. При вычислении интеграла (4) на 4-, 8-разрядном микроконтроллере без привлечения специализированных программ (MathCAD, MatLAB, Maple и т. д.) возникают проблемы из-за низкой разрядности двоичных чисел и отсутствия поддержки повышения точности (разрядности) вычислений, обычно применяемой в типовом программном обеспечении математических пакетов.

Проведенные исследования показали, что если при 32-разрядных вычислениях зафиксировать стандартное отклонение расстояний Хэмминга σ( h ) и изменять только математическое ожидание расстояний Хэмминга E ( h ), то мы получим почти линейную связь с оцениваемой энтропией (рис. 1).

При использовании малоразрядных процессоров экономически выгодно применять таблицы преобразований

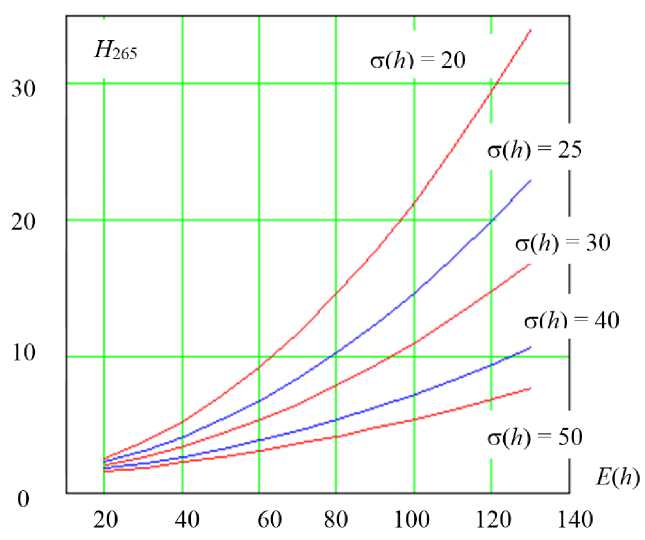
Р и с. 1. Почти линейная связь энтропии с математическим ожиданием расстояний Хэмминга при фиксированном стандартном отклонении

F i g. 1. Almost linear relationship between entropy and mathematical expectation of Humming distances at fixed standard deviation

с шагом записи данных 20 + 10 · i , где строчный индекс i меняется от 0 до 13 для математического ожидания расстояний Хэмминга E ( h ). Таблицы должны быть двухмерными, например, иметь 30 столбцов для значений стандартного отклонения σ( h ), изменяющегося на единицу. В ячейках двухмерной таблицы должны лежать значения энтропии номограммы, отображенной на рисунке 1.

Еще одним важным моментом является использование таблиц поправок значений энтропии DH ₂₅₆, которые компенсируют ошибку от проявления асимметрии закона распределения расстояний Хэмминга p ( h ).

Из рисунка 2 видно, что при значениях математического ожидания E ( h )=12,8, E ( h )=25,6 распределение расстояний Хэмминга становится существенно асимметричным [28; 29]. Это означает, что номограмма данных рисунка 1

при малых значениях математических ожиданий нуждается в значительных поправках DH ₂₅₆. Вычисление поправок выполняется путем нормирования расстояний Хэмминга, приводящего все возможные состояния к интервалу от 0 до 1. В итоге получается 8-разрядная двоичная таблица преобразований. Далее под заданное значение асимметрии подбираются два параметра бета-распределения. Уже в пространстве бета-распределений по формуле, аналогичной формуле (4), находится вероятность ошибок второго рода на 32-разрядной вычислительной машине:

P = f ¹----

2     ^J o B ( в 1, в 2)

■ h i ^e 1 - 1 ■ (1 - h) ^{e 2 - 1} ■ dh , (8)

где β 1, β 2 – параметры бета-распределения, обеспечивающие нуж-

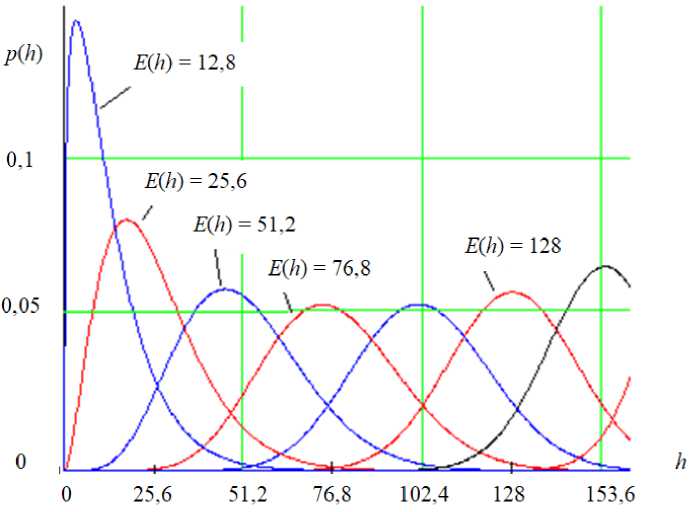
Р и с. 2. Распределение расстояний Хэмминга для одинаково коррелированных данных r = 0,33 и монотонно изменяющихся значений математического ожидания

F i g. 2. Distribution of Humming distances for equally correlated data r = 0.33 and monotonically changing values of mathematical expectation

ный показатель асимметрии полученного распределения Хэмминга;

B ( в 1, р 2) = J x ^{в 1 - 1} • (1 - x ) ^{в 2 - 1} • dx — бета 0

функция; h i = h /256 - нормированное расстояние Хэмминга.

Это и позволяет в конечном итоге синтезировать вторую таблицу поправок DH 256 для малых значений математического ожидания для E ( h ) < 70 бит.

Обсуждение и заключение

Таким образом, использование стан-дартизованых в России нейросетевых преобразователей биометрии в длинный код позволяет снизить вычислительную сложность оценки энтропии с экспоненциальной вычислительной сложности до линейной и одновременно экспоненциально снизить объем памяти, необходимой для хранения тестовых образов «Чужой». Кроме того, в новых условиях перехода в пространство расстояний Хэмминга удается сделать вычисление интегралов вероятности табличным (4), (8) (используются две таблицы размерами 12х30 и 7х30, которые хранят 8-битные значения энтропии и ее поправок).

Следует отметить, что биометрические приложения являются одними из самых глубокопроработанных и стандартизованных приложений искусственного интеллекта. Формально это обусловлено тем, что международный технический комитет по стандартизации ISO/IEC JTC 1/SC 37 (Биометрия) создан в 2002 г., а технический комитет ISO/IEC JTC 1/SC 42 (Искусственный интеллект) создан только в 2017 г. По этой причине международных стандартов по биометрии на текущий момент разработано и находится в разработке 160, тогда как стандартов по искусственному интеллекту разработано и находится в разработке только 11.

Все, что изложено в данной статье, проверено только на биометрических данных, однако авторы уверены в том, что нейросетевое распознавание биометрических образов является частным случаем распознавания образов произвольной природы нейросетевым искусственным интеллектом. При этом перенос достигнутого уровня тестирований и доверия биометрических приложений корректен только в том случае, когда применяются «широкие» нейронные сети, стандартизованные пакетом отечественных стандартов с номерами ГОСТов Р 52633. хх-20хх. Нейронные сети других классов, в том числе сверточные нейронные сети «глубокого» обучения, тестировать с применением быстрых алгоритмов вычисления энтропии нельзя10. Как следствие, доверие к ним должно быть значительно ниже, чем доверие к отечественным стандартизованным нейросетевым конструкциям.

Поступила 15.01.2020; принята к публикации 20.02.2020; опубликована онлайн 30.06.2020

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.