Быстродействие и отказоустойчивость идеальной системной сети через дополнительную параллельность

В статье рассматриваются возможности повышения характеристик системных сетей (распределенных коммутаторов) многопроцессорных вычислительных комплексов. Решается задача многократного повышения пропускной способности системных сетей и частичного резервировании их абонентов и каналов посредством копирования сетей и использования разветвителей каналов для подключения абонентов к разным копиям.

Задача решается посредством повышения сетевого быстродействия абонентов в результате параллельной передачи разных частей пакетов по разным каналам. Задача решается для системных сетей любой структуры (идеальные неблокируемые сети, традиционные многомерные гиперкубы, многомерные торы и т.п.) и размера (числа абонентов). При этом накладными затратами являются повышенная сложность вследствие использования копий сети и многократное использование адреса пакета в каждой его части, передаваемой независимо.

Решение задачи основывается на методах построения идеальных системных сетей с разными свойствами. Новизна решения состоит в сопряжении этих сетей для решения задачи повышения быстродействия системных сетей.

Идеальной системной сетью (ИСС) [1] считается сеть, которая обеспечивает соединение любых абонентов по прямым каналам (без промежуточной буферизации) при параллельной передаче пакетов данных от всех абонентов. Кроме того системная сеть считается идеальной, если она является неблокируемой (бесконфликтной) и самомаршрутизируемой на произвольных перестановках пакетов между абонентами.

ИСС рассматриваются в двух вариантах [2–5], с разными свойствами. В первом варианте это сети с топологией квазиполного графа [2, 3], изоморфного симметричной блок-схеме (block-design), изучаемой в комбинаторике [6]. Квазиполный граф — это двудольный граф, одну долю которого (хорду) составляют узлы, задающие полные m-портовые коммутаторы m х m, а другую долю—узлы, являющиеся m-портовыми абонентами. Любой узел в каждой доле связан ребрами (дуплексными каналами) с m разными узлами в другой доле. Кроме того, любые два абонента, связаны точно σ ⩽ m путями длины 2 через разные узлы другой доли (коммутаторы). Число узлов N в каждой доле задается через параметры m и а соотношением N = m(m — 1)/а + 1 и является максимально возможным.

Квазиполные графы (и симметричные блок-схемы) существуют не для всех значений параметров m и σ . Одни не существуют по определению (нецелое значение N ), другие по теории [6] , а третьи — просто не построены. Построение блок-схем это NP-сложная по m/а задача, которая при m >  12 и а ^ 2 практически еще не решена (блок-схемы не построены) [6 , 7] .

Если системная сеть имеет топологию квазиполного графа, то она является ИСС [2, 3] с σ разными путями между любыми двумя абонентами. Она также может задавать и распределенный самомаршрутизируемый полный коммутатор N х N .В этом случае каждый m-портовый абонент заменяется на однопортового абонента, подключенного через двусторонний разветвитель каналов (демультиплексор 1 х m от каждого абонента и мультиплексор m х 1 к каждому абоненту). Такой коммутатор можно инвариантно масштабировать по числу абонентов посредством увеличения числа коммутаторов и добавления каскада разветвителей каналов. Инвариантность проявляется в том, что сохраняются прямые каналы между абонентами, неблокируемость сети, самомаршрутизируемость по сети и число σ разных каналов между абонентами. К сожалению, вследствие некратности N и m масштабирование числа абонентов происходит достаточно медленно с увеличением числа каскадов разветвителей особенно при больших σ .

Особо отметим, что на основе любой системной сети с m абонентами можно построить расширенную системную сеть с N = m ( m — 1) /а + 1 абонентами и σ разными путями между ними. Для этого достаточно в сети с топологией квазиполного графа использовать в хорде копии исходной сети вместо коммутаторов. При этом любой путь проходит только через одну копию заданной сети с ее внутренними задержками. В такой расширенной сети возможно теряется неблокируемость и увеличиваются задержки передачи, но сохраняется возможность увеличения ее пропускной способности посредством параллельной передачи пакетов по разным путям. Расширенную сеть также можно масштабировать описанным способом по числу абонентов, сохраняя ее полную связность и число разных каналов между любыми абонентами.

Существует комбинаторный метод приближенного построения квазиполных графов для любых значений параметров m и σ . Это построение

1-расширенных квазиполных графов, в которых некоторые абоненты связаны σ + 1 ребрами, а остальные — точно σ ребрами, и число абонентов N ^∗ может быть на несколько единиц меньше N [8] . Такие расширенные квазиполные графы построены ниже для ряда m < 14 и σ < 10.

Использование ИСС с топологией квазиполного графа дает возможность многократно повышать скорость передачи пакетов по сети. Для этого достаточно разбивать пакеты на σ равных малых пакетов и параллельно передавать их по σ разным путям между абонентами. Накладными затратами при этом является необходимость передачи адреса приемника в каждом малом пакете и необходимость одновременной передачи малых пакетов от каждого абонента и приема их к нему. Кроме того, такой ИСС обеспечивает (ст — 1)-канальную отказоустойчивость сети и даже канальную живучесть с понижением скорости передачи пакетов при отказах каналов.

Главным недостатком ИСС с топологией квазиполного графа является малое число его абонентов и слабая наращиваемость при каскадном масштабировании. В данной работе решается задача преодоления этого недостатка, т.е. построения ИСС с любым числом абонентов при сохранении возможности иметь σ разных путей между абонентами.

Оба недостатка преодолеваются посредством использования ИСС с топологией квазиполного орграфа [4, 5] , который не имеет параллельных каналов. Эти ИСС изоморфны сетям со структурой двумерного гиперкуба. Они существуют при любых значениях m и только для σ = 1, и для них число абонентов задается соотношением N = m ² .

Эти ИСС образуют распределенные самомаршрутизируемые полные коммутаторы N х N . Для этого каждый m-портовый абонент заменяется на однопортового абонента, подключенного через двусторонние разветвители каналов 1 х m (мультиплексоры m х 1, демультиплексоры 1 х m).

Маршрутизаторы с такой топологией ( YARC и ROSSETA с внутренней буферизацией пакетов) с 64 и 48 портами используются в разных системных сетях [9 –11] . Полные коммутаторы с аналогичными параметрами позволяют строить ИСС с сотнями и тысячами абонентов. Так коммутаторы 64 х 64 позволяют создать ИСС с N = 4096 абонентами. Такая ИСС будет содержать N коммутаторов 64 х 64, каскад из N демультиплексоров 1 х 64 и каскад из N мультиплексоров 64 х 1.

Коммутаторы с топологией квазиполных орграфов допускают простое масштабирование числа абонентов без утраты свойства неблокируемости и самомаршрутизируемости на произвольных перестановках.

Оно осуществляется посредством каскадирования с использованием дополнительных слоев разветвителей каналов 1 х т . При этом возможно как внутреннее масштабирование с ростом числа абонентов в m раз, так и внешнее масштабирование с ростом числа абонентов в квадрат раз при каждом каскадировании.

В данной статье решается задача построения комбинированных ИСС с большим числом абонентов N ^ m 2 и числом параллельных путей между абонентами в диапазоне 3 ⩽ σ ⩽ 10 посредством разработки метода сопряжения ИСС с топологией квазиполных орграфов или любых системных сетей и ИСС с топологией квазиполных графов. Такие комбинированные ИСС обладают возможностью многократно повышать свою пропускную способность и сетевое быстродействие абонентов на основе исходной элементной базы.

В разделе 2 кратко представляются свойства ИСС с топологией квазиполного графа и строятся новые ИСС с большими значениями σ ( σ = 6 и σ = 10). В разделе 2 представляется метод расширения любых ИСС посредством внутреннего масштабирования с добавления еще одного каскада разветвителей канала. При этом ИСС расширяется как распределенный коммутатор с подключением однопортовых абонентов через каскад разветвителей каналов. Однако на заключительном шаге расширения крайний каскад собирается из многопортовых абонентов. Расширенная сеть состоит из набора копий исходной сети и приобретает возможность иметь σ разных каналов между любыми абонентами расширенной сети. Исследуются свойства этого метода при его каскадном применении.

Исследование показало, что при больших значениях σ это масштабирование эффективно только при однократном применении. В разделе 2 также показано, что метод внутреннего масштабирования применим не только для ИСС, но и для сетей с любой структурой (ИСС другой топологии, многомерных гиперкубов или торов). В этом случае данный метод дает возможность наделять группы сетей возможностью использовать разные каналы для повышения пропускной способности и канальной отказоустойчивости расширенной сети.

Для решения ранее поставленной задачи необходимо иметь возможность использовать системные сети любого размера (числа абонентов). В разделе 3 представляется метод построения ИСС с топологией квазиполного орграфа любого размера, имеющих ст = 1.

Сам метод основывается на начальном представлении ИСС как двудольного орграфа, который изоморфен двумерному гиперкубу. Он имеет хордовый каскад коммутаторов m х m, каскад разветвителей каналов 1 х m и объединяет N = m 2 абонентов. Такая ИСС многократно масштабируется как распределенный коммутатор посредством увеличения числа исходных малых коммутаторов и числа каскадов разветвителей каналов. При этом могут использоваться два метода масштабирования — внутренний и внешний.

Первый метод аналогичен методу расширения ИСС с топологией квазиполного графа, но поскольку в данном случае число абонентов кратно степени разветвителя каналов, то число абонентов (и число хордовых коммутаторов) увеличивается в m раз при каждом добавлении каскада разветвителей.

Второй метод масштабирует число абонентов (и число хордовых коммутаторов) посредством масштабирования уже имеющейся ИСС как исходной, но с использование каскадов разветвителей большого размера. Для сохранения элементной базы последние представляются как деревья исходных разветвителей. Такой метод внешнего масштабирования позволяет увеличивать число абонентов в квадрат раз при каждом применении каскада разветвителей все большего размера.

На базе ИСС с топологией квазиполных графов и орграфов в разделе 4 строятся и рассчитываются комбинированные ИСС, сочетающие возможности и свойства базовых ИСС. Сначала строятся ИСС с топологией квазиполных графов необходимого размера (числом абонентов). Затем они расширяются методом внутреннего масштабирования посредством использования необходимого числа их копий и добавления ИСС с m-портовыми абонентами (m ⩾ σ), использующей топологию квазиполных графов с заданным числом ст разных каналов (конкретно с ст = 6 и ст = 10). Таким образом, строятся комбинированные ИСС заданного размера и заданного числа разных каналов между абонентами. Кроме того, комбинированные ИСС строятся с разным числом добавляемых абонентов, в частности, без изменения их числа (m = ст) или с их удвоением (m и 2ст).

Для повышения сетевого быстродействия абонентов, передаваемые пакеты разбиваются на σ равных частей. Для полной загрузки σ разных каналов каждый абонент должен иметь равное число внешних сдвиговых регистров, которые параллельно передают свои части пакетов в соответствующие каналы или принимают эти части из них. Передача по прямым каналам обеспечивает минимальный диаметр в один скачок, а наличие нескольких разных параллельных каналов позволяет сочетать отказоустойчивость и многократно повышенную пропускную способность.

Эти свойства достигаются посредством использования многокаскадной струтуры ИСС. Базовый хордовый каскад содержит полные коммутаторы, промежуточные каскады — разветвители каналов, а внешний каскад содержит многопортовые абоненты, обеспечивающие наличие равное число разных каналов между ними. Такая ИСС имеет высокую схемную сложность [4] , которая при измерении в числе точек коммутации оценивается как O ( N 2 ). Обычно эта сложность распределена между N узлами сети.

Совсем не так обстоит дело в известных системных сетях меньшей сложности, поскольку задача построения неблокируемых отказоустойчивых системных сетей до настоящего времени не имеет полного решения.

Системная сеть является неблокируемой, если в ней для любой перестановки пакетов можно проложить бесконфликтные пути от источников к приемникам. Системная сеть является самомаршрутизируемой, если бесконфликтные пути можно проложить локально по узлам сети без их взаимодействия только на основе маршрутной информации в пакетах. Наконец, самомаршрутизация является статической, если любой источник может самостоятельно наметить бесконфликтные пути к своему приемнику.

Существование неблокируемых сетей было доказано еще Клозом [7, 8] . Однако пока еще не построено самомаршрутизируемых неблокируемых сетей Клоза. Поэтому сети Клоза используются только в более простых самомаршрутизируемых вариантах, которые не являются неблокируемыми сетями, а только перестраиваемыми сетями. Неблокируемыми являются 64–48 портовые коммутаторы YARK и ROSETTA, используемые как строительные блоки в ряде сетей разной структуры: перестраиваемой сети Клоза [9] , трехмерного гиперкуба [10, 11] , иерархии полных орграфов [12] . При этом сами эти сети не являются неблокируемыми.

Сети со структурой толстого дерева являются перестраиваемыми сетями Клоза [9] , в которых бесконфликтная передача осуществляется только по заранее составленным расписаниям для конкретных перестановок пакетов. Для произвольных перестановок эти сети оказываются блокируемыми, в которых произвольная перестановка полностью осуществляется за несколько скачков между узлами сети. Максимальное число таких скачков задает диаметр сети. В перестраиваемых сетях Клоза диаметр равен числу каскадов сети.

В литературе также широко представлены системные сети со структурой многомерного тора [13 –15] , использующие аналогичные небольшие коммутаторы в своих узлах. Эти сети для произвольных перестановок вообще не имеют возможности передавать пакеты по прямым каналам. В них произвольные перестановки осуществляются только за несколько скачков между узлами сети. Многомерные торы являются самыми простыми, но и самыми медленными сетями вследствие их больших диаметров, которые измеряется десятками скачков.

Наоборот сети со структурой иерархии полных или квазиполных орграфов [11, 12] имеют самый маленький диаметр в 3 скачка.

Сети со структурой обобщенного гиперкуба не являются даже перестраиваемыми сетями [16 –18] . Их можно сделать таковыми посредством увеличения числа каналов в некоторых измерениях. Обобщенные гиперкубы имеют диаметр равный числу измерений или на 1 меньше в расширенном гиперкубе [17] .

Большинство известных сетей не обладает канальной отказоустойчивостью без применения дополнительных мер. Например, гиперкуб обладает одноканальной отказоустойчивостью при удвоении числа каналов в каждом измерении [18] .

Аналогичным свойством обладает 6-мерный тор [15] , в котором только три измерения являются межузловыми, а остальные измерения реализуются внутри узлов.

В сетях со структурой иерархии полных или квазиполных орграфов [11 , 12] отказ канала приводит к увеличению диаметра сети с 3 до 5 скачков, т.е. к частичному уменьшению сетевого быстродействия абонентов и пропускной способности сети в целом.

Отказ каналов в сетях Клоза приводит к снижению пропускной способности сети, но не нарушает полной связности сети, т.к. в них имеется несколько каналов между абонентами, которые, однако, не могут использоваться абонентами параллельно.

В разделе 2 рассматриваются различные аспекты построения ИСС с топологией квазиполных графов. В разделе 3 рассматриваются различные аспекты построения ИСС с топологией квазиполных орграфов. Эти разделы содержат краткое изложение работ [2 –8] . В разделе 4 рассматриваются варианты построения ИСС с комбинированной топологией и характеристики такой ИСС.

2.    ИСС на основе топологии квазиполного графа

Квазиполный граф — это однородный двудольный граф, каждую долю которого составляют N узлов степени m. Значение m выбирается минимальным, при котором любые два узла в одной доле связаны σ ⩽ m прямыми путями длины два через разные узлы в другой доле. Если такой граф существует, то его параметры связаны соотношением N = m ( m — 1) /ст +1.

При схемной реализации узлы одной доли задаются как абоненты (процессоры) с m дуплексными портами, аузлыдругойдоли—как полные коммутаторы m x m с m дуплексными портами. Такую сеть мы называем простейшей и обозначаем ПС(N, т, ст). Она представлена на рисунке 1 при т = 4 и ст = 2.

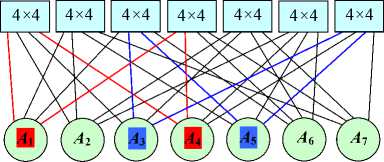
Рисунок 1. ИСС как ПС(7, 4, 2).

Сети ПС(N, т, ст ) изоморфны симметричным блок-схемам, исследуемым в комбинаторике. Матрица инцидентности квазиполного графа является симметричной блок-схемой B ( N,m, ст ), которая при т = 4 и ст = 2 задается в таблице 1. Теория блок-схем задает их существование в разрешимом виде, при котором они состоят из двух меньших блок-схем.

Таблица 1. Разрешимая блок-схема B(7,4, 2)

Блоки 4 х 4	Абоненты
1	1	2	3	4
2	1	2	5	7
3	1	3	5	6
4	1	4	6	7
5	2	3	6	7
6	2	4	5	6
7	3	4	5	7

Для построения блок-схем используются комбинаторные методы, которые представляют их в циклическом виде. Циклические блок схемы задаются по столбцам циклическими последовательностями (1,2,...,N), размещенных в i-x столбцах и начинающихся в строках a i ( i = 1, 2,..., m). При этом набор ( a 1 , a ₂ ,..., a m ) полностью задает циклическую блок-схему. В частности, блок-схема в таблице 2 задается набором (1,3,4, 5). Любые

Таблица 2. Циклическая блок-схема B(7,4, 2)

Блоки 4 х 4 Абоненты 1 1 6 5 4 2 2 7 6 5 3 3 1 7 6 4 4 2 1 7 5 5 3 2 1 6 6 4 3 2 7 7 5 4 3 циклические блок-схемы сводятся к разрешимым блок-схемам, но не наоборот, т.к. разрешимая блок-схема может не существовать в циклическом виде.

Для преодоления последнего недостатка было предложено использовать приближенные 1-расширенные циклические блок-схемы B*(N*,m,a*), в которых числа абонентов N∗ и разных путей σ∗ между любыми двумя абонентами подчиняется соотношениям N* ^ N и ст* ^ ст + 1, а число N* является максимальным для заданного значения m. Такие 1-расширенные блок-схемы могут быть построены комбинаторным способом для любых значения σ и m.

В данной работе это было сделано для разных значений m при ст = 6 и ст = 10, и полученные блок-схемы представлены в таблице 3. При

Таблица 3. Некоторые 1-расширенные циклические блок-схемы B * (N * ,m, 6) и B * (N * , m, 10)

B*(6, 6, 6) (1, 2, 3, 4, 5, 6) B*(10, 8, 6) (1, 2, 3, 4, 5, 6, 7, 8) B*(13, 9, 6) (1, 2, 3, 4, 5, 6, 8, 10, 11) B*(15,10, 6) (1, 2, 3, 4, 5, 6, 7, 9, 10, 12) B*(10,10,10) (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) B*(19,11, 6) (1, 2, 3, 4, 5, 7, 8, 11, 13, 15, 16) B*(22,12, 6) (1, 2, 3, 4, 5, 6, 7, 9, 11, 14, 17, 18) B*(14,12,10) (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12) B*(26,13, 6) (1, 2, 3, 4, 5, 6, 8, 11, 14, 16, 18, 22, 23) B*(16,13,10) (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14) B*(30,14, 6) (1, 2, 3, 4, 5, 6, 8, 11, 13, 14, 19, 20, 24, 28) B*(19,14,10) (1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 14, 15, 16) B*(35,15, 6) (1, 2, 3, 4, 5, 6, 8, 12, 15, 17, 21, 23, 28, 29, 33) B*(25,15,10) (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16) B*(39,16, 6) (1, 2, 3, 4, 5, 6, 8, 11, 14, 16, 20, 21, 25, 28, 32, 34) B*(24,16,10) (1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 14, 17, 18) этом некоторые 1-расширенные блок-схемы могут быть и простыми циклическими блок-схемами.

Очень часто m-портового абонента можно представить как однопортового абонента с разветвителем каналов 1 х m, в виде мультиплексора/де-мультиплексора во встречных каналах. В этом случае простейшая сеть ПС(N, m, ст) превращается в распределенный полный коммутатор N х N, обозначаемый как PK1(N1, m1, ст) с N1 = N и m1 = m. На рисунке 2 он показан для m = 4 и ст = 2 и расположен выше интерфейса с абонентами, обозначенного пунктирной линией.

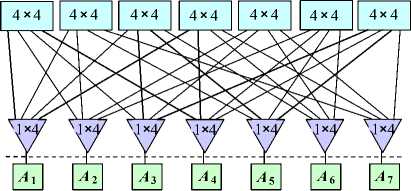
Рисунок 2. ИССкакРК 1 (7,4, 2).

Заметим, что при построении PK ₁ (N, m, ст ) мы фактически решили задачу масштабирования малого полного коммутатора m х m до большого коммутатора N х N, составленного из малых коммутаторов. При этом мы получили возможность иметь ст разных прямых путей между любыми абонентами в большом коммутаторе.

Последний коммутатор можно масштабировать и дальше двумя способами — внешним и внутренним каскадированием.

При внешнем каскадировании берется m 2 = N 1 и строится коммутатор РК ₂ (N ₂ ,m ₂ ,ст) с топологией квазиполного графа с N 2 = m ₂ ( m ₂ — 1)/ст + 1. Например, при m i =4 и ст = 2 имеем m 2 = 7 и N 2 = 22. Блок-схема В ⁽²2, 7 , ²⁾ не существует по теории, но построена 1^{-расширенная} блок-схема В * (21, 7, 2), задаваемая, например, набором (1, 2, 3, 5, 9,12,17).

Однако масштабирование коммутатора РК ₂ (^ ₂ ,m ₂ , ст) в коммутатор РК з (N з ,m з ,ст) с m 3 = N 2 уже практически невозможно, т.к. блок схема В ( N 3 ,m 3 , ст) с N 3 = m 3 ( m 3 — 1)/ст +1 скорее всего еще не построена ни в каком виде вследствие комбинаторных трудностей. В частности имеем m 3 = 22 и N 3 = 232.

При внутреннем каскадировании используются постоянная элементная база (коммутаторы m x m и разветвители каналов 1 x m), а масштабирование можно продолжать на любое число каскадов, но с более медленным ростом числа абонентов.

Внутреннее каскадирование состоит в построении расширенной простейшей сети, которая собирается из N 1 копий коммутатора РК ₁ (N ₁ ,m ₁ , ст).

Каждый из них разбивается на доли по m портов, и в каждой доле по всем коммутаторам строится отдельный составной коммутатор РК ₁ (N ₁ ,m ₁ , ст), но со сквозной нумерацией по всем ним. Эта нумерация является вторичной по отношению к внутренней нумерации в копиях исходного коммутатора и не зависит от нее.

В таблице 4 слева приводится пример таблицы инцидентности такой расширенной сети ( т 1 =4 и ст = 2) в предположении, что N 1 = rm 1 .

Таблица 4. Таблица инцидентности для каскадирования

РК 1 (7,4, 2)

РК 1	РПС(14,4, 2)								РК 2 (11,4, 2)
Порты	1	2	3	4	5	6	7	8	1	2	3	4	5	6	7
1	1	2	3	4	8	9	10	11	1	2	3	4	8	9	10
2	1	2	5	7	8	9	12	14	1	2	5	7	8	9	11
3	1	3	5	6	8	10	12	13	1	3	5	6	8	10
4	1	4	6	7	8	11	13	14	1	4	6	7	8	11
5	2	3	6	7	9	10	13	14	2	3	6	7	9	10
6	2	4	5	6	9	11	12	13	2	4	5	6	9	11
7	3	4	5	7	10	11	12	14	3	4	5	7	10	11

В этом случае число абонентов в расширенной сети оказывается N 2 = rN 1 , и по построению не уменьшается число разных путей между абонентами, т.к. их число равно или ст или m 1 .

Однако в PK ₁ (N ₁ , m 1 , ст) число N 1 не кратно m 1 и расширенная сеть преобразуется в PK ₂ (N ₂ , m 1 , ст), в котором N 2 < rN 1 . В таблице 4 справа приводится пример таблицы инцидентности РК ₂ (N ₂ ,m ₁ ,ст), На рисунке 3 приводится схема РК ₂ (N ₂ ,m ₁ , ст), построенного по таблице 3.

Построение соединений осуществляется следующим образом. По номерам абонентов в таблице каскадирования коммутатора РК 1 ( N 1 , m 1 , ст ) находятся номера его копий через которые проходит соединение. Например, в таблице 4 абоненты 2 и 8 соединяются через коммутаторы 1 и 2. По порядковым номерам абонентов в таблице определяются номера портов соответствующих коммутаторов PK ₁ (N ₁ , m 1 , ст). Например, в таблице 4

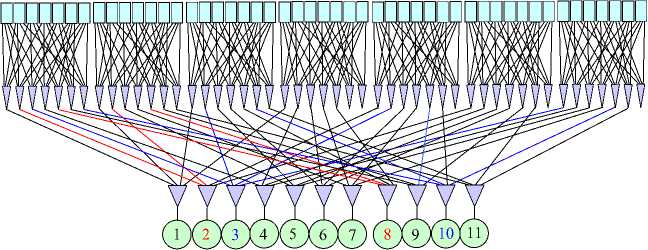
Рисунок 3. РК 2 (11,4, 2), полученный посредством внутреннего расширения РК 1 (7,4, 2).

порядковые номера абоненты 2 и 8 это 2 и 5, которые задают номера портов коммутаторов 1 и 2.

Коммутатор PK 2 (N 2 ,m ₁ , ст), задает ИСС с большим числом абонентов чем коммутатор PK 1 (N 1 , m 1 , ст), но не с меньшим числом разных путей между любыми двумя абонентами. Масштабирование ИСС можно продолжать и дальше посредством каскадирования коммутаторов PK i (N i , m 1 , ст). При этом для рассматриваемого примера образуется следующая последовательность коммутаторов РК ₃ (18,4, 2), РК ₄ (31,4, 2), РК 5 (52, 4, 2), РК 6 (91,4, 2), РК 7 (152,4, 2) и РК 8 (266,4, 2), каждый из которых является ИСС с не меньше чем 2 разными путями между абонентами. Еще меньшее масштабирование числа абонентов происходит при каскадировании коммутатора РК 1 (5,4, 3) при котором последовательность ИСС состоит из РК 2 (6, 4, 3), РК з (7, 4, 3), РК 4 (8, 4, 3) и РК 5 (10,4, 3).

Фактически масштабирование ИСС с топологией квазиполного графа оказалось малоэффективным кроме первого шага построения коммутатора PK 1 (N 2 , m i , ст), при котором увеличилось как число абонентов, так и число разных каналов между ними. Но такое преобразование (инвариантное расширение) может быть применено к системной сети любой структуры.

Пусть у нас имеется исходная сеть ИС(М) на M абонентов (рисунок 4 слева), к которой применяется процедура внутреннего расширения с использованием N = m ( m — 1)/ст + 1 копий ИС(М). При этом образуется расширенная сеть РС(М * ) с M * = [ M/m j N + 4 абонентами при 0 <  5 < N , в которой имеется ст разных путей между любыми абонентами (рисунок 4 справа).

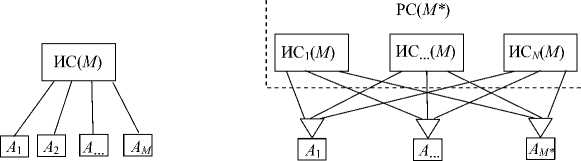
Рисунок 4. Инвариантное расширение системной сети

Рассмотренный подход уже использовался применительно к системной сети «Ангара» [12] для возможного повышения ряда ее характеристик [13, 14] . Ровно так же он может быть использован и для повышения ее быстродействия (раздел 4) . В данной работе в качестве сетей ИС(М) далее рассматриваются ИСС с топологией квазиполного орграфа с ст = 1, которые допускают любое масштабирование. Они кратко представляются в следующем разделе.

3.    ИСС на основе топологии квазиполного орграфа

В данном разделе строятся неблокируемые самомаршрутизируемые распределенные коммутаторы на базе коммутаторов с топологией квазиполных орграфов. Для них возможна любая степень масштабирования числа каналов посредством внутреннего и внешнего каскадирования. Они базируются на двумерном гиперкубе, построенном из m-канальных коммутаторов m х m. На рисунке 5 приводится пример двумерного гиперкуба.

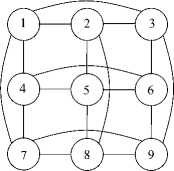
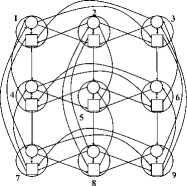
Рисунок 5. Двумерный троичный гиперкуб при m = 3 как граф и орграф

В о ргр афе (рисунок 5 справа) каждый узел содержит m-портового абонента (круг) и m-канального коммутатора m х m (квадрат) , которые связанны m входными и m выходными дугами. В таком представлении двумер ны й m- ичн ы гиперкуб может быть преставл как дудольный орграф с N = m ² узлами в каждой доле (рисунок 6) , который именуется квазиполным орграфом.

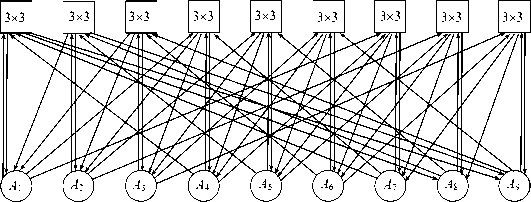
Рисунок 6. Квазиполный орграф при m = 3

Соединения в нем задаются разными таблицами инцидентности для дуг от абонентов и дуг к абонентам (таблицы 5 и 6) . Они существуют при любых m.

Таблица 5. Таблица инцидентности для квазиполного орграфа при m = 3

Коммутаторы	Дуги от абонентов			Дуги к абонентам
1	1	2	3	1	4	7
2	1	2	3	2	5	8
3	1	2	3	3	6	9
4	4	5	6	1	4	7
5	4	5	6	2	5	8
6	4	5	6	3	6	9
7	7	8	9	1	4	7
8	7	8	9	2	5	8
9	7	8	9	3	6	9

Таблица 6. Таблица инцидентности для квазиполного орграфа при произвольном m

Коммутаторы	Дуги от абонентов				Дуги к абонентам
1	1	2	...	m	1	1 + m	...	1 + m(m — 1)
2	1	2	...	m	2	2 + m	...	2 + m(m — 1)
...	1	2	...	m	...	...	...	...
m	1	2	...	m	m	m + m	...	m + m(m — 1)
m + 1	m + 1	m + 2	...	m + m	1	1 + m	...	1 + m(m — 1)
m + 2	m + 1	m + 2	...	m + m	2	2 + m	...	2 + m(m — 1)
...	m + 1	m + 2	...	m + m	...	...	...	...
m + m	m + 1	m + 2	...	m + m	m	m + m	...	m + m(m — 1)
...	...	...	...	...	...	...	...	...
m 2 — m + 1	m 2 — m + 1	m 2 — m + 2	...	m 2	1	1 + m	...	1 + m(m — 1)
...	m 2 — m + 1	m 2 — m + 2	...	m 2	2	2 + m	...	2 + m(m — 1)
m 2 — 1	m 2 — m + 1	m 2 — m + 2	...	m 2	...	...	...	...
m 2	m 2 — m + 1	m 2 — m + 2	...	m 2	m	m + m	...	m + m(m — 1)

Быстродействие и отказоустойчивость идеальной системной сети       57

Для подсоединения однопортовых абонентов используются демультиплексоры 1 х m и мультиплексоры m х 1 соответственно (рисунок 7) . Таким образом получается неблокируемый самомаршрутизируемый распре-

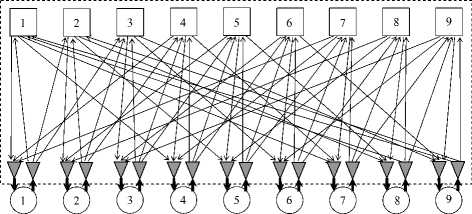
Рисунок 7. Коммутатор РК 1 (9, 3) с топологией квазиполного орграфа при т = 3

деленный коммутатор PK 1 (N, m). В нем маршрутизации осуществляется от источника по адресам (номерам) выходных портов демультиплексоров и коммутаторов. Бесконфликтная передача пакетов на произвольной их перестановке осуществляется по прямым каналам за один скачок от источников к приемникам, т.е. с максимальным быстродействием.

Посредством внутреннего масштабирования можно построить ряд коммутаторов PK i (N i ,m) с N i = m i+1 . Каждый коммутатор PKi(N i ,m) строится из N = m 2 коммутаторов РК _i-1 (N _i-1 , m) и слоя из N i демультиплексоров 1 х m и мультиплексоров m х 1.

Например, при m = 4 получим ряд коммутаторов с 16, 64, 256, и 1024 абонентами. Аналогично при m = 16 — ряд коммутаторов с 256, 4096 и 65536 абонентами.

При внешнем масштабировании можно построить ряд коммутаторов PK j ( N j , m j ) для J = 2i(i = 1,2,...) с N j = N j/2 и m j = N j/2 , начиная с PK 1 (N 1 , m 1 ) при N 1 = N и m 1 = m.

Можно построить коммутатор PK 2 (N 2 ,m ² ) на основе коммутатора РК 1 (N 1 ,m 1 ) и слоя мультиплексоров m 1 х 1 и демультиплексоров 1 х m 1 с m 1 = N 1 = m 2 . Он имеет N 2 = N 2 = m ⁴ каналов и по построению сохраняет неблокируемость и самомаршрутизируемость коммутатора PK 1 (Ni,m 1 ). Если демультиплексоры и мультиплексоры можно строить как деревья из исходных демультиплексоров 1 х m и мультиплексоров m х 1, то их общее число в дополнительном слое равно N 1 ( m + 1).

Также, можно построить коммутатор РK 4 (N 4 ,m 4 ) на основе коммутатора РK ₂ (N ₂ , т ² ) и мультиплексоров т 4 х 1 и демультиплексоров 1 х т ₄ с т ₄ = N 2 = т ⁴ . Он имеет N 4 = N 2 = т ⁸ каналов сохраняет неблокируемость и самомаршрутизируемость коммутатора РK ₂ (N ₂ ,m ² ).

Если демультиплексоры и мультиплексоры строить в виде деревьев из демультиплексоров 1 х т и мультиплексоров т х 1, то их общее число в дополнительном слое равно N ₂ ( m ³ + т ² + т + 1).

Например, для т = 4 при внешнем каскадировании получим ряд коммутаторов с 16, 256 и 65536 абонентами.

4.    ИСС на основе комбинированной топологии

Сопряжение коммутаторов разных топологий осуществляется как внутреннее расширение коммутатора РK г ( N _i , m _i ) с топологией квазиполного орграфа, при котором на последнем шаге используется коммутатор с топологией квазиполного графа РK ₁ (N, т,ст). Такой расширенный коммутатор будем обозначать как РРК(М, N _i ,m _i , N, т, ст), где M задает число его абонентов определяемое как M = \ N_i/m \ N + 5, где 0 <  6 < N . Построенный расширенный коммутатор является неблокируемой само-маршрутизируемой системной сетью с прямыми каналами, т.е. ИСС, которая объединяет M абонентов и имеет ст разных прямых путей между любыми двумя абонентами.

Для примера в таблицах 7 и 8 приводятся таблицы инцидентности для внутреннего расширения коммутатора РК ₂ (16, 4) коммутаторами РК 1 (5,4, 3) и РК 1 (7, 5, 3). При этом последний коммутатор изоморфен 1-расширенной блок-схеме B * (7, 5, 3) с 3 или 4 разными путями между абонентами.

Таблица 7. Таблица инцидентности коммутатора

РРК(20,16,4, 5,4, 3)

РК 2	РРК(20,16,4, 5, 4, 3) с S = 0
Порты	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1	1	2	3	4	6	7	8	9	11	12	13	14	16	17	18	19
2	1	2	3	5	6	7	8	10	11	12	13	15	16	17	18	20
3	1	2	4	5	6	7	9	10	11	12	14	15	16	17	19	20
4	1	3	4	5	6	8	9	10	11	13	14	15	16	18	19	20
5	2	3	4	5	7	8	9	10	12	13	14	15	17	18	19	20

Таблица 8. Таблица инцидентности коммутатора

РРК(22,16,4, 7, 5, 3)

РК 2	РРК(22,16,4, 7, 5, 3) с 5 = 1
Порты	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1	1	2	3	4	5	8	9	10	11	12	15	16	17	18	19	22
2	1	2	3	4	7	8	9	10	11	14	15	16	17	18	21	22
3	1	2	3	6	7	8	9	10	13	14	15	16	17	20	21	22
4	1	2	5	6	7	8	9	12	13	14	15	16	19	20	21	22
5	1	4	5	6	7	8	11	12	13	14	15	18	19	20	21	22
6	2	3	4	5	6	9	10	11	12	13	16	17	18	19	20
7	3	4	5	6	7	10	11	12	13	14	17	18	19	20	21

Можно на последнем шаге мас ия вместо коммутатора PK i (N, m, ст) с однопортовыми абонентами ( к 2) использовать простейшую сеть ПС(N, т, ст) с m-портовыми абонентами (рисунок 1) . В этом случае коммутатор РРК(М, N i , m i , N, т, ст) превращается в расширенную сеть РПС(М, N i ,m i , N, т, ст), в которой возможна одновременная бесконфликтная передача по σ разным путям д двумя абонентами. Будем характеризовать расширенную щими параметрами: числом абонентов M , числом добавленны нентов D = M — N i сложностью S , задаваемую как число копий коммутатора РKi(N _i , m i ), используемых на последнем шаге расширения, т.е. S = N . Выбор параметров сети ПС(N, m, ст ) будем осуществлять посредством максимизации критерия g = ctD /S . Значения критерия вычисляются по формуле g = ст/m — ст²/ ( m ( m — 1) + ст) и приводятся в таблице 9 и графиком на рисунке 8 с точностью до двух знаков.

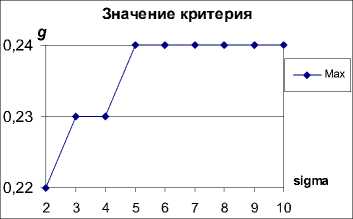
Рисунок 8. Значения критерия g

Таблица 9. Значения критерия g

m \ σ	2	3	4	5	6	7	8	9	10
2	0,00
3	0,17	0,00
4	0,21	0,15	0,00
5	0,22	0,21	0,13	0,00
6	0,21	0,23	0,20	0,12	0,00
7	0,19	0,23	0,22	0,18	0,11	0,00
8	0,18	0,22	0,23	0,22	0,17	0,10	0,00
9	0,17	0,21	0,23	0,23	0,21	0,16	0,09	0,00
10	0,16	0,20	0,23	0,24	0,23	0,19	0,15	0,08	0,00
11	0,15	0,19	0,22	0,24	0,24	0,22	0,18	0,14	0,08
12	0,14	0,18	0,22	0,23	0,24	0,23	0,21	0,18	0,13
13	0,13	0,17	0,21	0,23	0,24	0,24	0,23	0,20	0,17
14	0,12	0,17	0,20	0,22	0,24	0,24	0,23	0,22	0,19
15	0,11	0,16	0,19	0,22	0,23	0,24	0,24	0,23	0,21
16	0,11	0,15	0,18	0,21	0,23	0,24	0,24	0,24	0,23
17	0,10	0,14	0,18	0,20	0,22	0,24	0,24	0,24	0,23
18	0,10	0,14	0,17	0,20	0,22	0,23	0,24	0,24	0,24
19	0,09	0,13	0,16	0,19	0,21	0,23	0,24	0,24	0,24
20	0,09	0,13	0,16	0,19	0,21	0,22	0,24	0,24	0,24
21	0,09	0,12	0,15	0,18	0,20	0,22	0,23	0,24	0,24
22	0,08	0,12	0,15	0,17	0,20	0,21	0,23	0,24	0,24
23	0,08	0,11	0,14	0,17	0,19	0,21	0,22	0,23	0,24
24	0,08	0,11	0,14	0,16	0,19	0,20	0,22	0,23	0,24
25	0,07	0,11	0,13	0,16	0,18	0,20	0,21	0,23	0,24
26	0,07	0,10	0,13	0,15	0,18	0,19	0,21	0,22	0,23
27	0,07	0,10	0,13	0,15	0,17	0,19	0,21	0,22	0,23
28	0,07	0,10	0,12	0,15	0,17	0,19	0,20	0,22	0,23
29	0,06	0,09	0,12	0,14	0,16	0,18	0,20	0,21	0,22
30	0,06	0,09	0,12	0,14	0,16	0,18	0,19	0,21	0,22

Максимальные значения критерия g имеют верхнюю и нижнюю границы, которые представлены графиком на рисунке 9. В эти границы

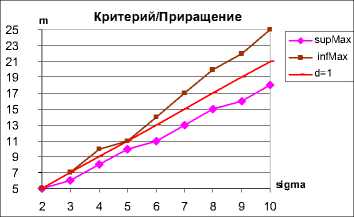
Рисунок 9. Верхние и нижние границы максимальных значений критерия g укладывается значения D « Ni, задаваемые отношением d « D/Ni « 1.

Примеры того, какие ИСС можно построить на сопряжении коммутатора РК 3 (4096,16) и сети ПС(N, т, 6) (см. таблица 3 и таблица 9) , приведены в таблице 10 .

Таблица 10. Примеры ИСС на основе РК ₃ (4096,16) и nC(N, m, 6)

Сеть	Расширение	D	S
ПС(6, 6, 6)	РПС(4096, 4096, 16, 6, 6, 6)	0	6
ПС(10, 8, 6)	РПС(5120, 4096, 16, 10, 8, 6)	1024	10
ПС(26, 13, 6)	РПС(7510, 4096, 16, 26, 13, 6)	4096	26
ПС(10, 10, 10)	РПС(4096, 4096, 16, 10, 10, 10)	0	10
ПС(14, 12, 10)	РПС(4783, 4096, 16, 14, 12, 10)	687	14
ПС(24, 16, 10)	РПС(6144, 4096, 16, 24, 16, 10)	2048	24

Основными целями построения ИСС на основе РПС(М, N i ,m i , N, т, ст) являются повышение ее быстродействия и отказоустойчивости.

Быстродействие повышается посредством разбиения пакетов на части и параллельной передачей частей по разным путям между источниками и приемниками. Накладными затратами при этом являются необходимость иметь отдельного заголовка с адресом приемника в каждой части и повышенная сложность ИСС вследствие использования копий исходной (расширяемой) сети.

Отказоустойчивость в ИСС повышается посредством резервирования в ней как каналов, так и абонентов. При этом если параллельно исполь- зовать σ∗ < σ путей между абонентами, то отказоустойчивость ИСС можно обеспечить и по ее быстродействию. При уменьшении числа разных путей меньше σ∗ работоспособность ИСС может сохраняться посредством уменьшения ее быстродействия, что обеспечивает ее канальную живучесть.

Повышенное быстродействие ИСС можно использовать для создания в вычислительной системе групп из ст +1 абонентов с повышенной отказоустойчивостью. Эти абоненты решают одну и ту же задачу (может по разным алгоритмам) с периодической сверкой результатов. Для сверки результатов каждый абонент посылает свой результат остальным участникам группы в одном сеансе по σ разным путям с предварительной синхронизацией этой рассылки. Правильным считается результат, совпадающий по большинству (может относительному) абонентов.

Порты m-портового абонента можно реализовать как набор виртуальных сдвиговых регистров (рисунок 10) . Внутри абонента пакеты в них

Порт1 ^… Порт i … Порт m

СР1 СР i СР m

Рисунок 10. Структура m-портового абонента.

заносится независимо, но запускается на сдвиг (передачу) одновременно. Наоборот, пакеты в регистры принимаются из сети асинхронно, но считываются одновременно. В каждом сеансе задействуются только σ регистров. Поэтому сеанс задается не только заполнением регистров, но и маской, которая выделяет σ задействованных регистров.

Для выравнивания времен обмена пакетами со сдвиговыми регистрами внутри абонента и между абонентами по сети можно иметь несколько наборов сдвиговых регистров, используемых попеременно. Эти наборы в совокупности образуют многопортовую сетевую карту с параллельными портами.

Заключение

В статье рассмотрен метод дополнительного распараллеливания системных сетей. Он применим к любым системным сетям как метод их инвариантного расширения на основе простейших сетей с топологией квазиполного графа (раздел 2) . Этот метод применим даже к идеальным системным сетям с казалось бы наибольшей параллельностью, которая обеспечивает их неблокируемость на произвольных перестановках при любых их размерах (раздел 3)

В статье рассмотрен метод использования дополнительной параллельности системных сетей для повышения их пропускной способности вместе с абонентским быстродействием и повышения канальной и абонентской отказоустойчивости. Рассмотренный метод может быть использован применительно к системной сети «Ангара», имеющей структуру одномерного, двумерного либо трёхмерного тора.