Быстрое восстановление смазанного изображения, полученного горизонтально вращающейся камерой

В данной статье рассматривается восстановление смазанного изображения, получаемого вращающейся горизонтально с равномерной скоростью камерой.

Метод Люси–Ричардсона [1 –3] восстанавливает смазанные изображения более общего происхождения, чем в данной работе, работает с матрицей общего вида и требует C ∙ N ² операций, где N – количество пикселей в строке изображения, константа C пропорциональна количеству итераций, которое может иметь порядок нескольких десятков [2]. К близким работам можно отнести методы коррекции изображений в подвижных системах [4, 5]. Известно много методов фильтрации шумов и размытостей изображений, которые сводятся к решениям уравнений или вычислениям операторов типа свертки с компактным носителем (опорной областью, функцией рассеяния точки) [6], [7]. К таким же методам относятся и итерационный алгоритм Ван Циттерта [8], фильтр Винера [9] и др.

Быстрый алгоритм восстановления смазанного изображения представлен в статье [10].

Рассматриваемая в данной работе задача приводит к решению уравнения дискретной свертки на циклической группе с ядром – характеристической функции сегмента. Величина этого сегмента (длина смаза) определяется скоростью вращения камеры и может быть сопоставима с размерностью изображения, что отличает данную задачу от [6], [7]. Представленная статья продолжает исследования авторов [11 – 14], в которых был разработан быстрый алгоритм решения рассматриваемой задачи, исследовались погрешности получаемого решения (качества восстановленного изображения) в случае невырожденной матрицы дискретной свертки и была представлена зависимость числа обусловленности матрицы, получаемой СЛАУ (системой линейных ал-

Следует отметить, что метод фильтра Винера не применим к рассматриваемой в данной статье задаче, поскольку этот метод предполагает (после преобразования Фурье) деление на символ исходного оператора свертки, который в данном случае вырожден.

В работе [14] описана зависимость качества восстановления изображения (числа обусловленности матрицы модельной системы) от скорости вращения снимающей камеры и построен график такой зависимости. В данной работе получены график и формулы зависимости качества восстановленного изображения от размерности матрицы для невырожденного случая. На основании этих формул делаются оценки качества восстановленного изображения для вырожденного случая. Приводятся примеры с оценками СКО (средне квадратичного отклонения).

Математическая модель задачи восстановления смазанных цилиндрических панорам и ее особенности

Будем рассматривать идеальную ситуацию, в которой смаз на матрице цифровой камеры происходит строго горизонтально. Будем считать, что изображение равномерно сдвигается вправо относительно матрицы цифровой камеры на к пикселей. Пусть {x ij}еMmxN - исходное изображение, которое мы будем представлять как цилиндрическую панораму разрешением m^N. Тогда смазанное изображение будет вычисляться по формуле yj =

x j + ^xy ® 1 + ... + x ij e ( к - 1)

k где i = 1,2,..., m, j = 1,2,...,N, ® - сложение по модулю N. Для восстановления изображения для каждой строки Xi исходного изображения необходимо решить уравнение

AX? = kYiт, где Yi - соответствующая строка смазанного изображения (символ т означает транспонирование), A -циклическая матрица размеров NхN вида

	( 1 0	1 1	••• 1 ••• 1	1 1	0 1	0 0	0 0	••• 0 ••• 0	0 0
	••• 0	••• 0	••• ••• ••• 1	••• 1	••• 1	••• 1	••• 1	••• ••• ••• 0	••• 0
	0	0	••• 0	1	1	1	1	••• 0	0
A =	0	0	••• 0	0	1	1	1	••• 1	0	.(1)
	0	0	••• 0	0	0	1	1	••• 1	1
	1	0	••• 0	0	0	0	1	••• 1	1
	1	1	••• 0	0	0	0	0	••• 1	1
	• • • ч 1	••• 1	••• ••• ••• 1	••• 0	••• 0	••• 0	••• 0	••• ••• ••• 0	••• 1 ,

В каждой строке и каждом столбце последней матрицы содержится ровно к единиц. В работе [12] показано, что ранг матрицы A вычисляется по формуле r = rang(A) = N - НОД(N, к) +1.

Здесь и далее будем использовать обозначение: НОД - наибольший общий делитель. Из данной формулы, в частности, вытекает, что матрица A - обратима тогда и только тогда, когда НОД ( N , к ) = 1.

Если матрица СЛАУ вырождена, то в силу того, что она совместна, она имеет бесконечно много решений. Это множество представляет собой некоторую гиперплоскость в N -мерном пространстве ( N -количество неизвестных в системе). Все координаты вектора решений СЛАУ могут быть представлены в виде линейной комбинации ( N - r ) параметров (параметры общие для всех строк изображения). Если пиксель представлен l -битным словом (наиболее распространен вариант l =8 - один байт), то среди бесконечного множества решений следует искать те, которые находятся в N -мерном кубе [0,2 ¹ -1] N .

Алгоритм преобразования исходной СЛАУ

Рассмотрим СЛАУ

AX = Y

с матрицей A вида (1). Предлагаемый алгоритм решения СЛАУ будет использовать только элементарные преобразования строк. При описании алгоритма будем иллюстрировать только основную матрицу системы. При этом программа, реализующая данный алгоритм, должна работать только с правой частью, поскольку преобразования основной матрицы системы известны до начала работы программы. Таким образом, используемая память программы - N чисел (правая часть системы уравнений).

Из каждого уравнения вычтем последующее, а из последнего уравнения - первое. Эта серия преобразований не равносильная. В результате получим СЛАУ

A'X = Y' (3)

с матрицей

	( 1 0	0 ••• 1 •••	0 0	0 0	-1 0	0 -1	0 ••• 0 •••	0 0	0 ^ 0
	• • • 0	••• ••• 0 •••	••• 1	••• 0	••• 0	••• 0	••• ••• 0 •••	••• 0	••• 0
	0	0 •••	0	1	0	0	0 •••	-1	0
A =	0	0 •••	0	0	1	0	0 •••	0	-1	.(4)
	-1	0 •••	0	0	0	1	0 •••	0	0
	0	—1 • • •	0	0	0	0	1 •••	0	0
	••• 0	••• ••• 0 •••	••• -1	••• 0	••• 0	••• 0	••• ••• 0 •••	••• 1	••• 0
	0	0 • • •	0	—1	0	0	0 •••	0	1

Теорема 1 . Ранг матрицы (4) на единицу меньше ранга матрицы (1). Если к матрице (4) добавить строку с номером N - к +1 из (1), то получим матрицу

	r 1	0 •••	0	0	-1	0	0 •••	0	0 л
	0	1 •••	0	0	0	-1	0 •••	0	0
	••• 0	••• ••• 0 •••	••• 1	••• 0	••• 0	••• 0	••• ••• 0 •••	••• 0	••• 0
	0	0 •••	0	1	0	0	0 •••	-1	0
A " =	0 -1	0 ••• 0 •••	0 0	0 0	1 0	0 1	0 ••• 0 •••	0 0	-1 0	(5)
	0	-1 • • •	0	0	0	0	1 • • •	0	0
	••• 0	••• ••• 0 •••	••• -1	••• 0	••• 0	••• 0	••• ••• 0 •••	••• 1	••• 0
	0	0 •••	0	-1	0	0	0 •••	0	1
	0	0 •••	0	0	0	1	1 •••	1	1

^XN - к + j ^{+ X}N - к + j + d ^{+ X}N - к + j + 2 d +    + ^XN - d + j

= Q j

Полученная подсистема с параметром обратима, так как НОД ( N / d , k / d )= 1. Для всех j = 0, 1,…, ( d – 1) матрицы подсистем одинаковы, отличия только в правой части и имени параметра. Таким образом, все подсистемы можно решать одновременно с одной матрицей и многими различными правыми частями.

Пример восстановления смазанного изображения в случае вырожденной модельной матрицы

Проиллюстрируем изложенные выше соображения на примере N = 10, k =4. Для данного примера d = НОД ( N , k )=2. Система уравнений (3) принимает вид

размером ( N + 1)× N с рангом, равным рангу матрицы (1) (см. [11]).

Очевидно, что СЛАУ A " X = H , где правая часть H имеет вид H = ( y‘,у ‘,•••, у N , y „ _ k + 1 ) ^т , равносильна СЛАУ (2).

Сведение задачи восстановления изображений с вырожденной СЛАУ к решению параметризованных задач с невырожденной СЛАУ

Рассмотрим случай, в котором числа N и k не являются взаимно простыми. Пусть d = НОД ( N , k ). Тогда СЛАУ (3) распадается на d независимых СЛАУ. Для каждого j =0, 1,…, ( d – 1) в уравнения с номерами i = 0, 1,…, N , для которых i = j (mod N ), входят только переменные с такими же номерами i = j (mod N ), причем эти переменные не входят ни в какие другие уравнения. Получается d СЛАУ вида (2) с одинаковыми матрицами размера N / d , у которых ненулевые элементы «1» и «– 1» стоят в столбцах, номера которых отличаются на величину k / d (mod N / d ). Поскольку числа N / d и k / d взаимно простые, то ранг этой матрицы равен ( N / d – 1). Если добавить к этой матрице строку, у которой первые ( N / d – k / d ) элементов нули, а последние k / d единицы, то получится матрица ранга N / d .

Введем массив параметров Q j , j = 0, 1,…, ( d – 1), которыми обозначим частичные суммы переменных

^XN - к + 1 ^{+ X}N - k + 1 + d ^{+ X}N - k + 1 + 2 d +    + ^XN - d + 1

= Q 1 ,

^XN - к + 2 ^{+ X}N - к + 2 + d ^{+ X}N - к + 2 + 2 d +    + x N - d + 2 = Q 2 ,

(6) ..............................

^XN - к + d ^{+ X}N - к + 2 d ⁺ x N - к + 3 d ⁺ ' ' ' ^{+ X}N Q d -

Из равенств (6) и последнего уравнения СЛАУ с матрицей (5) вытекает, что все d параметров связываются одним уравнением

^Q 1 ^{+ Q} 2 +^{+ Q}d - 1 ^{+ Q}d = ^HN + 1 ,

где H N + 1 = Y N – k + 1 . Теперь для каждого j =0, 1,…, ( d – 1) сгруппируем уравнения с номерами i =0, 1,…, N , для которых i = j (mod N ), в одну подсистему и припишем к ней j -е уравнение из (6)

X 1 - X 5 = H 1 , X 2 - X 6 = H 2 , x 3 - X 7 = H 3 , X 4 - X 8 = H 4 ,

X 5 - X 9 = H 5 ,

X 6 - X 10 = H 6 , - ^X 1 + ^X 7 = H 7 - ^X 2 + ^X 8 = H ₈ - ^X 3 + ^X 9 = H 9

- ^X 4 + ^X 10 = H 10 .

Эта система распадается на две независимых системы по пять уравнений с пятью неизвестными: одна состоит из уравнений с нечетными номерами и нечетными переменными, а другая – с четными. При переходе к СЛАУ с матрицей (5) к этим системам добавляется еще одно уравнение

x ₇ + x ₈ + x ₉ + x ₁₀ = H 11 .

Это уравнение можно заменить тремя уравнениями, введя две новые переменные Q 1 и Q 2 :

[ X 7 + X 9 = Q 1 ,

^ X 8 + X 10 = Q 2 ,

I Q 1 + Q 2 = H 11 .

Теперь СЛАУ с матрицей (3) для рассматриваемого примера ( N = 10, k =4) можно представить следующим образом:

<

X 1 - X 5 = H 1 , X 3 - X 7 = H 3 , X 5 - X 9 = H 5 ,

■ X 1 + X 7 = H 7 , ■ x ₃ + x ₉ = H ₉,

I x 7 + x 9 = Q 1 .

X 2 - X 6 = H 2 , X 4 - X 8 = H 4 , _e X 6 - X 10 = H 6 ,

■ X 2 + X 8 = H 8 ,

■ X 4 + X 10 = H 10 ,

_ X 8 + X 10 = Q 2 .

Здесь Q 1 + Q 2 = H 11 .

Матрицы обеих подсистем (6) и (7) одинаковы, а правые части имеют вид

( H _ь H 3 , H 5 , H 7 , H 9 ,0) ^т + (0,0,0,0,0, Q1Y

Рис. 1. Исходное изображение. Количество пикселей в строке N = 720

и

( H 2 , H 4 , H 6 , H ₈, H ю,0) ^т + (0,0,0,0,0, Q 2 ) ^T .

Каждая из двух подсистем обратима относительно входящих в нее пяти координат вектора X , но имеет параметр Q i или Q ₂ соответственно. Систему (6) можно решать алгоритмом, описанным в [14], но с двумя правыми частями ( H i , H 3 , H 5 , H 9 ,0) ^т и (0,0,0,0,0, Q i )^T. Систему (7) можно решать аналогично. Очевидно, что решения обеих систем со второй правой частью будут одинаковы. Решение системы (6) с правой частью (0,0,0,0,0, Q i ) ^T нетрудно найти, оно равно (1/2) ( Q i , Q i , Q i , Q i , Q i , Q i ), что легко проверяется.

Рис. 2. Изображение, смазанное на 43 пикселя

Общее решение СЛАУ будет получено в виде:

X i = R i + Q -, x 2 = r 2 + Q 2 ,

X 3 = R 3 + q ¹ , X 4 = R 4 + Q 4

Рис. 3. Величина смаза k = 43. НОД(720, 43) = 1

x5 = R5 + , x 6 = R 6 + ^2- , y — R 4- Q r — R _1_ QL x7 = R7 + 2 , x8 = R8 + 2 ,

X 9 = R 9 + %, X i0 = R i0 + Q ²- , 2              2

где

Рис. 4. Величина смаза k = 86. НОД(720, 86) = 2

Q i + Q 2 = H ii .

Частное решение задачи восстановления изображений с вырожденной СЛАУ

Все решения рассматриваемой СЛАУ описываются параметрами Q i , Q 2,..., Q d -i , Q d , которые связаны соотношением

^Q i ^{+ Q} 2 ⁺ • • • ^{+ Q}d - i ^{+ Q}d = H N + i .

В данной работе (эвристически) рассмотрены значения параметров

Рис. 5. Величина смаза k = 8. НОД(720, 8) = 8

Q i = Q 2 =••• = Q d - i = Q d = H Nf^ d

.

Такая фиксация параметров приводит к достаточно качественным восстановлениям изображений, которые представлены на следующих рисунках.

На рис. I представлено исходное изображение. На рис. 2 приведено смазанное изображение. Далее будем приводить только восстановленные изображения при разных величинах смаза.

Рис. 6. Величина смаза k = 24. НОД(720, 24) = 24

На рис. 3 - 8 представлены восстановленные изображения при различных величинах смаза.

Из представленных на рисунках восстановленных изображений видно, что с увеличением наибольшего общего делителя НОД ( N , к ) качество восстановления изображения снижается, но для разумных значений параметров остается приемлемым.

Рис. 7. Величина смаза k = 90. НОД(720, 90) = 90

Рис. 8. Величина смаза k = 120. НОД(720, 120) = 120

Оценки погрешностей при получении рассматриваемого частного решения задачи восстановления изображений с вырожденной СЛАУ

Качество восстановления изображения зависит от погрешностей при решении СЛАУ, моделирующей смазанное изображение. Эти погрешности в значительной степени определяются числом обусловленности матрицы СЛАУ. В прежней работе авторов [14] (случай невырожденной СЛАУ) показан график зависимости числа обусловленности матрицы СЛАУ от величины смаза k при фиксированной размерности матрицы. В данном параграфе приведем анализ и графики зависимости числа обусловленности матрицы (1) от размерности матрицы при фиксированной величине смаза k .

Предположим, что условие обратимости матрицы выполнено, и найдем ее число обусловленности Cond ( A ) = || A ||∙|| A ^–1||. Под нормой матрицы будем понимать норму оператора умножения на эту матрицу, индуцированную евклидовой нормой.

Теорема 2 . Число обусловленности матрицы A находится по формуле

Cond ( A ) = max

1 + £-1 + £ -2 + • • • + £ - k+1

1     p-1 -к p^-2 -I- • • • -I- - kk ⁺¹

1 + £ j + £ j + + £ j

где £ i , £ j - комплексные корни степени N из единицы.

Доказательство. Так как преобразование Фурье изометрическое, то

I A|| = ||F 1 AF\I = ddigg (Xo, Xb • ••, X n-1 )|| = max |X i | j A-1|| = ||F-1A-1 F|| = | diag (Xo1, X-1, •••, X --1)||

= max |X i ¹1

m^n |x i i

где X i - собственные числа матрицы A , которые становятся диагональными элементами после преобразования Фурье. Отсюда

Cond ( A ) = mEix

Xi

X j

= max

1 + £-1 + £ -2 + • • • + £-k+1

1 + £—1 + £—2 + • • • + £—+1

Теорема доказана.

Расчеты показывают, что число обусловленности существенно зависит от соотношения между N и k . Для N = k ∙ m + l число обусловленности растет линейно по m при фиксированном l = 1, 2,…, k – 1. График зависимости Cond ( A ) от N при k = 17 показан на рис. 9.

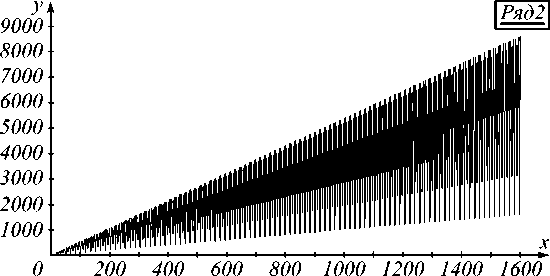
Рис. 9. График зависимости числа обусловленности от ширины изображения при величине смаза, равной 17

Таким образом, поскольку решение вырожденной СЛАУ размерности N сводится к решению N / d независимых невырожденных СЛАУ, можно сделать вывод о том, что погрешности при вычислении рассматриваемого частного решения вырожденной СЛАУ оцениваются меньшей величиной (в d раз), чем для невырожденной СЛАУ той же размерности. График зависимости погрешности (среднеквадратичное отклонение восстановленного изображения от исходного) от величины смаза показан на рис. 10.

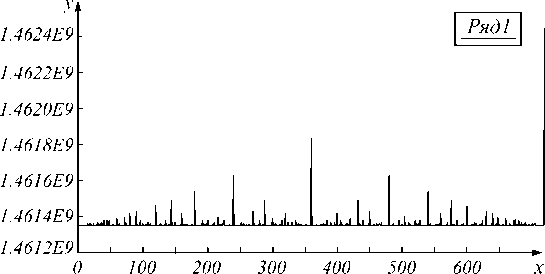
Рис. 10. График зависимости СКО от величины смаза при фиксированном количестве пикселей в строке N = 720

Отклонение восстановленного отображения от исходного эталона состоит из двух слагаемых:

• 1)    Отклонение, вызванное ростом погрешности начальных данных. Это отклонение ограничено погрешностью начальных данных умноженной на число обусловленности матрицы СЛАУ. Погрешность начальных данных зависит от количества бит

для хранения пикселя.

• 2)    Отклонение, вызванное выбором конкретного решения из линейного многообразия решений. Всплески на графике находятся в точках, для которых величина НОД ( N , k ) имеет большое значение и, следовательно, размерность многообразия решений велика.

Заключение

В данной статье, которая является развитием предшествующих работ, рассматривается проблема построения быстрого алгоритма восстановления смазанных изображений с оценками качества восстановления. Авторам видится следующий путь к решению этой проблемы: сначала получить решение проблемы в простых частных случаях, а затем более сложные задачи сводить к изученным простым. В данной статье сделан очередной шаг на этом пути: получен быстрый алгоритм восстановления изображения, смазанного при горизонтально вращающейся камере, в случае вырожденной системы уравнений математической модели; получены оценки качества восстановленных изображений.