Быстрые алгоритмы дискретных косинусных преобразований

Автор: Чичева М.А.

Журнал: Компьютерная оптика @computer-optics

Рубрика: Обработка изображений: Восстановление изображений, выявление признаков, распознавание образов

Статья в выпуске: 16, 1996 года.

Бесплатный доступ

Разработаны быстрые алгоритмы ДКП-II, III и IV нечетной длины. Приведены оценки вычислительной сложности алгоритмов при N=3exp(r). Показаны преимущества синтезированных алгоритмов перед традиционным ДКП-I четной длины.

Короткий адрес: https://sciup.org/14058317

IDR: 14058317

Текст научной статьи Быстрые алгоритмы дискретных косинусных преобразований

Широкое использование дискретного косинусного преобразования (ДКП)

„ , _ N —¹ , _ I ( n + 12 ) m )

x, ( m ) = 1/ ( n ) cos П — (1)

n =0 ( N )

в различных задачах цифровой обработки сигналов объясняется, по меньшей мере, тремя причинами.

Во-первых, базисные функции ДКП хорошо аппроксимируют собственные функции преобразования Карунена-Лоэва для широкого класса стационарных случайных процессов [1, 2], что делает ДКП эффективным средством кодирования информации.

Во-вторых, дискретный сигнал, наблюдаемый на конечном интервале [0, N -1], представленный в виде линейной комбинации базисных функций ДКП продолжается как 2 N -периодическая функция на множество целых чисел Z . Следствием увеличения периода является отсутствие или значительное снижение краевых эффектов при блочном кодировании.

В-третьих, для ДКП существуют быстрые алгоритмы (БА) вычисления спектра (1).

Отметим, что предложенный в [1] БА ДКП сводит вычисление (1) к вычислению дискретного преобразования Фурье (ДПФ) вещественной последовательности длины 2 N :

x ( m ) =

N -1 N -1

to m 2 E x ( n ) ® m" + ®~ m ² E x ( n ) ® n =0 n =0

снизить вычислительную сложность БА ДОП, в частности, ДКП.

Действительно, в схеме декомпозиции алгоритма (2) явным образом проводятся вычисления с числами exp { 2 n l *n ⁺ ₂1 Nm } . Значения базисных функ-

ций ДКП

( (n+12)m \ cos (n SN^ ) =

- ¹ (exn / ⁽ n ^+V2) m 1 ⁽ n ^+V2) m 1)

= 2 ( ^exp { ² ⁿ ‘ ₂ N } ⁺ ^exp { ² ⁿ ^l ₂ N } )

имеют в два раза меньшую степень алгебраичности над Q , что позволяет снизить вычислительную

сложность БА ДКП еще приблизительно в два раза по сравнению с алгоритмом работы [2].

Наиболее эффективно эти соображения реализуются в случае нечетного N [4, 5]. Дополнительный вычислительный эффект может быть получен при применении “нетрадиционного” представления комплексных чисел, согласованного со структурой алгоритма ДКП. Например [5, 6], при N = 3 r целе-

сообразно использование представления комплексных z в форме

z = a y + b y ,

у = exp

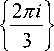
В ряде работ [7, 8] наряду с каноническим косинусным преобразованием (1) (далее, ДКП-I) рассматривались другие типы ДКП:

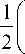
„ z x N-1 z A I n (m + xH (m) = ^x (n) cos I n—--- x 7 n=o 7 I N

(ДКП-II)

1 2 N -1

¹ m 2 mk

= 3^ю E y (^k) ^ю ,

² k =0

, , x N z A I nm xn, (m) = 2_,x(n)cos n — x 7 n=o ' I N.

(ДКП-III)

где ю = exp {^} , y ( k ) - вещественная последовательность длины 2 N , полученная четным продолжением x ( n ):

- ( \ \ ' \ I ( ⁿ ⁺ 12 )v x,„ ( m ) = ^ x ( n ) cos П----—

' n :0 ^x ' ( N

У ⁽ ^k ) =

x (k)

x ( 2 N — k — 1 )

0 < k < N — 1

N < k < 2 N — 1 '

(ДКП-IV)

Целью настоящей работы является перенесение методики синтеза БА ДКП работ [4, 5] для ДКП-II-IV.

Использование БА ДПФ “совмещенного” типа [2] позволяет вычислять спектр (1) с помощью ДПФ комплексной последовательности длины N .

В работе [3] указано, что специфические арифметические свойства значений базисных функций дискретных ортогональных преобразований (ДОП) позволяют в значительной степени

1. Сведение ДКП-IV к вещественному ДПФ той же длины

Рассмотрим ДКП-IV:

x IV ( ^m ) =

N —I I

^ x (n) cos I П n=0Q I

( n + 12 )( m + }2 )

1 2 n +i)(2 m +1) I

= Re, Z-iXyn) ®^V ) ,

I n =0 J

где to = exp {^} - первообразный корень степени 8N из единицы. Пусть x (n) •рЦ k = 2 n +1;

0 •рЦ k = 2 n ;

y (t ) = XIV (m) •рЦ t = 2m +1, тогда (4) примет вид

J2 N-1

y (t ) = Re 1E У (k) to‘ f .

I n=0

При нечетном N выполним декомпозицию Гуда-Томаса [9]. Пусть

J k = 8 k _i + Nk ₂ ( mod 8 N )

[t ^ 8ati + Nbt2 (mod 8N) ’ где a и b определяются из условий:

J 8 ² a ^ 8 ( mod 8 N )

| N ² b = N ( mod 8 N )

Введем обозначения:

а = exp {n} , p = exp{Jn} — первообразные корни из единицы степени 8 и N соответственно;

Y ( k i , k 2 ) = y ( 8 k i + Nk 2 ) , ( k i , k 2 ) g K ,v ;

Y ( t i , 1 2 ) = У ( 8 at i + Nbt 2 ) , ( t i , 1 2 ) e M_№ ;

K_IV , M_IV - допустимые области значений входных ( k_i,k ₂ ) и выходных ( t_i,1 ₂ ) пар индексов, определяемые диапазоном изменения переменных k и t (примеры областей K_IV , M_IV для N = 9, 27 приведены на рис. 1, 2).

	k 2									K IV
7	63	71	7	15	23	31	39	47	55
6	54	62	70	6	14	22	30	38	46
5	45	53	61	69	5	13	21	29	37
4	36	44	52	60	68	4	12	20	28
3	27	35	43	51	59	67	3	11	19
2	18	26	34	42	50	58	66	2	10
1	9	17	25	33	41	49	57	65	1
0	0	8	16	24	32	40	48	56	64	k 1
	0 ^t 2	1	2	3	4	5	6	7	8	M IV
7	63	55	47	39	31	23	15	7	71
6	54	46	38	30	22	14	6	70	62
5	45	37	29	21	13	5	69	61	53
4	36	28	20	12	4	68	60	52	44
3	27	19	11	3	67	59	51	43	35
2	18	10	2	66	58	50	42	34	26
1	9	1	65	57	49	41	33	25	17
0	0	64	56	48	40	32	24	16	8	t 1
	0	1	2	3	4	5	6	7	8

Рис. 1. Допустимые области значений пар

( k , , k ₂ ) и ( t _i, 1 ₂ ) дляДКП-IV при N = 9 ( a = 8 , b = i ).

	k 2							K IV
7	189	197	205	213	5	13	21	29	37	45	53	61	69	77	85	93	101	109	117	125	133	141	149	157	165	173	181
6	162	170	178	186	194	202	210	2	10	18	26	34	42	50	58	66	74	82	90	98	106	114	122	130	138	146	154
5	135	143	151	159	167	175	183	191	199	207	215	7	15	23	31	39	47	55	63	71	79	87	95	103	111	119	127
4	108	116	124	132	140	148	156	164	172	180	188	196	204	212	4	12	20	28	36	44	52	60	68	76	84	92	100
3	81	89	97	105	113	121	129	137	145	153	161	169	177	185	193	201	209	1	9	17	25	33	41	49	57	65	73
2	54	62	70	78	86	94	102	110	118	126	134	142	150	158	166	174	182	190	198	206	214	6	14	22	30	38	46
1	27	35	43	51	59	67	75	83	91	99	107	115	123	131	139	147	155	163	171	179	187	195	203	211	3	11	19
0	0	8	16	24	32	40	48	56	64	72	80	88	96	104	112	120	128	136	144	152	160	168	176	184	192	200	208	k 1
	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26

	t 2							M IV
7	135	55	191	111	31	167	87	7	143	63	199	119	39	175	95	15	153	71	207	127	47	183	103	23	159	79	215
6	54	190	110	30	166	86	6	142	62	198	118	38	174	94	14	150	70	206	126	46	182	102	22	158	78	214	134
5	189	109	29	165	85	5	141	61	197	117	37	173	93	13	149	69	205	125	45	181	101	21	157	77	213	133	53
4	108	28	164	84	4	140	60	196	116	36	172	92	12	148	68	204	124	44	180	100	20	156	76	212	132	52	188
3	27	163	83	3	139	59	195	115	35	171	91	11	147	67	203	123	43	179	99	19	155	75	211	131	51	187	107
2	162	82	2	138	58	194	114	34	170	90	10	146	66	202	122	42	178	98	18	154	74	210	130	50	186	106	26
1	81	1	137	57	193	113	33	169	89	9	145	65	201	121	41	177	97	17	153	73	209	129	49	185	105	25	161
0	0	136	56	192	112	32	168	88	8	144	64	200	120	40	176	96	16	152	72	208	128	48	184	104	24	160	80	t 1
	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26

Рис. 2. Допустимые области значений пар ( k _i, k ₂ ) и ( t _i, 1 ₂ ) для ДКП-IV при N = 27 ( a = i7 , b = 3 ).

Учтем, что ( к₁, к 2 ) е K IV только при нечетных к 2 , а именно, к 2 = 1, 3, 5, 7 .

Преобразуем теперь (5) следующим образом:

Y ( t 1 , t 2 ) = Re J У Y ( k i , к 2 ) e k 1 t a ²'² l ( k i , к 2 ) е K iv

= Re ^ У Y (кi,1) в1 at2 + У Y (кi,3) ^^ta3 *2 +

[ ( ^к 1Л )^е K iv ( ^к 1 ,³ )^е K iv

+ У Y ( к 1 ,5 ) p ^' a ⁵ t ² + У Y ( к _p7 ) p ^' a ⁷ t ² ( ^к 1 ,⁵ )^е K IV ( ^к 1 ,⁷ )^е K IV

= Re ^ У Y ( к , 1 ) в ^k ¹ ^t a ^t ² + У Y ( к ,3 ) в N - ^к ¹ ⁾ ¹¹ ( - 1 ) ¹ ² a ² +

[ ( ^к 1 ,¹ )^е K iv ( ^к 1 ,³ )^е K iv

+ У y(к ,5)вt(-1)12 a2

У Y ( к₁ ,7 ) в N ^- ^к ¹ ⁾ t a t ²

⁽ ^к 1 ,⁷ ⁾ ^е K iv

⁽ ^к 1 ,5 )^е K iv

Откуда, учитывая нечетность t ₂ (при

( t , t 2 ) е M V ), окончательно получим

I N -1 I

Y ( t 1 , t 2 ) = Re ^ a ² У z ( к 1 ) /Г , (6)

[ к =0

где

z (к1 ) =

Y ( к , 1 )

- Y (N - к ,7) - Y (к ,5)

Y ( N - к ,3 )

при при при при

( к , 1 ) е K iv ( к ,3 ) е K iv ( к ,5 ) е K iv ( к ,7 ) е K iv

ческих операций S_iv ( N ) для выполнения ДКП-IV указанным способом не превышает:

M_iv ( N ) < N log₃ N - N ^,

A iv ( N ) < 3 N log 3 N + 4 N

S iv ( N ) < 4 N log 3 N + N

2. Быстрый алгоритм ДКП-II.

Рассмотрим ДКП-II нечетной длины N :

Функция z ( к ) является некоторой перестановкой исходной последовательности со сменой знака части компонент. При нечетном t ₂ умножение на a ² в (6) требует только двух операций сложения на отсчет и может быть выполнено одновременно с нормировкой.

Таким образом, ДКП-IV нечетной длины N сведено к вещественному преобразованию Фурье той же длины. При N=3^r использование алгоритма ДПФ с представлением данных в форме (3) требует

M ( N ) = N log₃ N - N

Л x_II

N -1 /

( m ) = "^x ( n ) cos I n

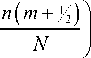
Г N -1

= Re । У x ( n ) ® ⁽ 2 m ⁺ ¹ )

L n =0

A (N ) = 3 N log3 N - 5N операций вещественного умножения и сложения соответственно. Тогда число умножений Miv (N) , сложений Aiv (N) и общее количество арифмети

где го = exp { ;4 N } . Очевидно [1], что ДКП-II (с точностью до нормирующих множителей) является преобразованием обратным к ДКП-I, поэтому при выполнении декомпозиции Гуда-Томаса достаточно поменять местами области допустимых значений. Примеры таких областей K_II , M_II для N = 9, 27 приведены на рис. 3, 4.

Пусть

y (к ) = ( x(n1 v ’ [0

при к = 2 n + 1; при к = 2 n ;

x (m) = y (2 m +1) ;

( k„ к 2 ) e K ,, , ^;

( m_pm 2 ) e M„ , ^;

Y ( k , k ₂) = x ( 4 ak + Nbk₂ )

;

Y ( m_x , m₂ ) = x ( 4 m , + Nm ₂) ;

где a и b определяются из условий:

4 2 a = 4 ( mod 4 N )

N ² b = N ( mod 4 N ) .

При этом (7) можно представить в виде:

Y ( m i , m 2 ) =

= Re I E Y ( k 1 , k 2 ) в '"" i^k ² m ²

Ц k ' , k 2 )e K„

где в = exp {^} - первообразный корень степени N из единицы. Учитывая, что при ( m 1 , m ₂ ) е M_H m ₂ -нечетно, получим из (8) для m ₂ = ' :

Y (m',') = Re j E Y (k', k2) в' m'ik2 [(k,.k2 )eK, а для m2 = 3 с учетом вещественности Y (kp k2) :

Y ( m „3) = Re ^ E Y ( k ' , k 2 ) e k ' m ' i 3 k ² [ ( k ' , k 2 )^e K II

= Re j E Y ( k ' , k 2 ) в "N ^- m ' ) i k ² > - [ ( k 1 , k 2 )^e K II

k 2 K II 3 27 19 11 3 31 23 15 7 35 2 18 10 2 30 22 14 6 34 26 1 9 1 29 21 13 5 33 25 17 0 0 28 20 12 4 32 24 16 8 k 1 0 1 2 3 4 5 6 7 8 m 2 M II

3	27	31	35	3	7	11	15	19	23
2	18	22	26	30	34	2	6	10	14
1	9	13	17	21	25	29	33	1	5
0	0	4	8	12	16	20	24	28	32	m 1

0 1 2 3 4 5 6 7 8

Рис. 3. Допустимые области значений пар ( k , . k ₂ ) и ( m , . m ₂ ) для ДКП-II при n = 9 ( a = 7 , ь =' ).

	k 2															K II
3	27	55	83	3	31	59	87	7	35	63	91	11	39	67	95	15	43	71	99	19	47	75	103	23	51	79	107
2	54	82	2	30	58	86	6	34	62	90	10	38	66	94	14	42	70	98	18	46	74	102	22	50	78	106	26
1	81	1	29	57	85	5	33	61	89	9	37	65	93	13	41	69	97	17	45	73	101	21	49	77	105	25	53
0	0	28	56	84	4	32	60	88	8	36	64	92	12	40	68	96	16	44	72	100	20	48	76	104	24	52	80	k 1
	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26
	m 2																											M II
3	81	85	89	93	97	101	105	1	5	9	13	17	21	25	29	33	37	41	45	49	53	57	61	65	69	73	77
2	54	58	62	66	70	74	78	82	86	90	94	98	102	106	2	6	10	14	18	22	26	30	34	38	42	46	50
1	27	31	35	39	43	47	51	55	59	63	67	71	75	79	83	87	91	95	99	103	107	3	7	11	15	19	23
0	0	4	8	12	16	20	24	28	32	36	40	44	48	52	56	60	64	68	72	76	80	84	88	92	96	100	104	m 1
	0	1 2 Рис. 4.		3 4 5 6 7 8 Допустимые области						9 10 11 12 значений пар				13 ( k ' , k 2	14 ) и	15 ⁽ m ' ,	16 m 2 )	17 18 19 20 21 для ДКП-II при n =					22 23 27 ( a =		24 , b	25 = ³ ).	26

Откуда получим:

j N -'

z ( m ' , m 2 ) = Re ^ E z ( k ' ) в ' m '

I k ' =0

где

[ Y € ( m ^l ) при ( ^m 1^, l ) e M i,

£( m,, m2 ) = < ;

^ Y € ( N - m _p3 ) при ( m ₁,3 ) G M I,

z ( k ' ) = Y ( k ' , k ₂ ) i ^k ² при ( k ' , k ₂ ) e K I .

Здесь значения входной последовательности z ( k ' ) являются вещественными или чисто мнимы -ми, что позволяет использовать несложную модификацию вещественного ДПФ с несколько увеличенным числом умножений. Выполнение такого алгоритма ДКП-II требует

M I ( N ) < 2 N log₃ N - 2 N ,

A ,, ( N ) < 3 N log₃ N - -

S,, (N)< 5N log3 N - 8N операций умножения, сложения и всего арифметических операций, соответственно.

3. Алгоритм вычисления ДКП-III

Рассмотрим ДКП-III:

( nm ) cos n— .

V N J

ZX x ˆ _III

(m ) = £ x (n)

n =0

Отметим, что длина этого преобразования равна N + 1 , однако оно может быть сведено к вещественному ДПФ длины 2 N следующим простым приемом. Так как при n = N справедливо равенство

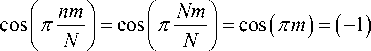
то

xiii (m) =

N T¹ ( nm ^ mm

= ^ x (n) cos I n— l + (-1) x (N) =

n =0 V ^N J

( 2 N -1 1

= Re К y (n) ®nm k(-1)mx (N) ,

I n =0

где ю = exp { 2 N } ,

. , f x (n) при 0 < n < N;

У (n) = ^

[ 0 при N < n < 2 N .

Таким образом, вычисление ДКП-III длины N +1 отличается от вычисления ДПФ вещественной последовательности длины 2N только N вещественными сложениями и, при использовании упомянутого выше БА ДПФ при N = 3 r , для вычислительной сложности ДКП-III справедливы неравенства:

M I,, ( N ) < 2 N log₃ N - 2 N ,

А_ш ( N ) < 6 N log 3 N - 7N ,

S i,, ( N ) < 8 N log 3 N - ^f .

4. Сравнение сложности алгоритмов

Рассмотрим более подробно сложность описанных алгоритмов при малых длинах N .

Как уже отмечалось во введении, специфические свойства ДКП делают его привлекательным при решении ряда задач цифровой обработки изображений, в частности, в задачах распознавания образов (для вычисления локальных признаков на изображении) и сжатия данных (при блочном формировании трансформант). Таким образом, используется ДКП сравнительно небольших размеров. Приведем точные оценки количества арифметических операций, необходимых для вычисления ДКП-I-IV длины N = 9, 27.

Преобразование Фурье с представлением данных в форме (3) при N = 9 требует всего 6 вещественных умножений и 38 сложений; при N = 27 требуется 42 умножения и 194 сложений. Дополнительно при переходе от представления комплексных чисел в форме (3) к алгебраической форме при вычислении ДКП-I и IV длины N необходимо N -¹ операций вещественного умножения и N операций вещественного сложения, для ДКП-II и III - только N операций сложения.

Арифметическая сложность рассмотренных алгоритмов для N = 9 и 27 приведена в таблице 1.

Таблица 1.

N	ДКП-I					ДКП-II	ДКП-III				ДКП-IV
N	M ( N )	A ( N )	S ( N )	M ( N )	A ( N )	S ( N )	M ( N )	A ( N )	S ( N )	M ( N )	A ( N )	S ( N )
9	10	56	66	12	56	68	12	94	106	10	74	84
27	55	248	303	86	248	334	84	442	526	55	302	357

В таблице 2 для сравнения приведено число операций для выполнения ДКП-I близких длин при N = 2 r традиционным способом сведения к ДПФ вещественной последовательности двойной длины:

Реальные затраты машинного времени на выполнение блочного ДКП размера N х N (при построчно-столбцовом способе формирования двумерного преобразования) для обработки изображения размером 1024 x 1024 отсчета приведены на рис.5. (Время приводится в условных единицах, все алгоритмы тестировались в одинаковых условиях).

Таблица 2.

N	ДКП-I
	M ( N )	A ( N )	S ( N )
8	15	79	94
16	51	221	272
32	147	551	698

Здесь 1 - время обработки изображения при использовании ДКП-I, 2 - ДКП-II, 3 - ДКП-III, 4 -ДКП-IV и 5 - время обработки при использовании ДКП-I длины N = 2 r , выполненного традиционным способом [1].

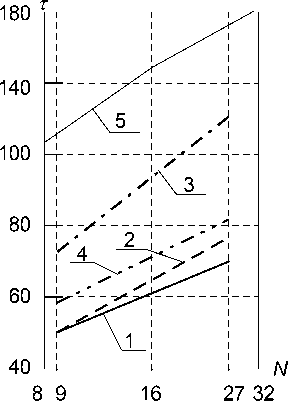
Рис.5.

Заключение

В данной работе разработаны алгоритмы ДКП-II, III и IV нечетной длины N . Приведены оценки вычислительной сложности алгоритмов при N = 3 r , проведено сравнение их быстродействия при малых длинах N = 9, 27. Показаны преимущества синтезированных алгоритмов перед традиционным ДКП-I четной длины при близких значениях N .

Рассмотренные алгоритмы ДКП являются основой для синтеза построчно - столбцовых алгоритмов двумерных дискретных косинусных преобразований. Для синтеза БА ДКП, существенно использующих двумерность и вещественность входных данных, возможно применение методики работы [6], в основе которой лежит представление данных в виде элементов алгебры кватернионов [10]. Вычислительная сложность таких алгоритмов определяется, в основном, сложностью соответствующих БА ДПФ, подробно исследованных в работе [11] автора.

Работа выполнена при поддержке Российского Фонда Фундаментальных Исследований (проект N95-01-00367).

Статья научная

3	27	31	35	3	7	11	15	19	23
2	18	22	26	30	34	2	6	10	14
1	9	13	17	21	25	29	33	1	5
0	0	4	8	12	16	20	24	28	32	m 1

3	27	31	35	3	7	11	15	19	23
2	18	22	26	30	34	2	6	10	14
1	9	13	17	21	25	29	33	1	5
0	0	4	8	12	16	20	24	28	32	m 1

3	27	31	35	3	7	11	15	19	23
2	18	22	26	30	34	2	6	10	14
1	9	13	17	21	25	29	33	1	5
0	0	4	8	12	16	20	24	28	32	m 1