Быстрый алгоритм медианной фильтрации

Медианная фильтрация является удобным инструментом обработки информации, особенно двухмерной информации — изображения [1, 2, 3]. Медианный фильтр удаляет из сигнала фрагменты с размерами, меньшими чем половина размера окна фильтра, и при этом мало искажает или почти совсем не искажает остальные участки сигнала. Например, одномерный монотонный сигнал совсем не искажается медианным фильтром. Наиболее известным применением медианной фильтрации является устранение из сигнала коротких импульсных помех [2, 3]. Причем амплитуда помехи не влияет на результат медианной фильтрации в отличие от реакции линейного фильтра. В работе [1] показано использование медианного фильтра при обработке изображения клеток крови — гранулоцитов. Здесь перед измерением размера гранулоцита его изображение подвергалось сглаживанию медианным фильтром с целью устранения гранул, которые могут влиять на результат измерения.

Обычно в процессе медианной фильтрации значения сигнала в некоторой окрестности точки, в которой вычисляется отклик фильтра, при помощи сортировки по возрастанию или убыванию выстраиваются в вариационный ряд. Отклик фильтра определяется как медиана — значение сигнала середины (центра) вариационного ряда. В дальнейшем эту окрестность будем называть окном фильтра. Кроме того, для упрощения будем рассматривать фильтр с квадратным окном размером n х n. Следовательно, при вычислении медианы в окне фильтра число операций с данными, например число операций сортировки, равно n ² .

При обработке изображения размером M х N точек (пикселей) число операций с данными будет велико и составит M х N х n2. Различные опера- ции требуют разных затрат времени выполнения. При последовательном сканировании изображения количество наиболее трудоемких операций — операций сортировки можно сократить. Так, при переходе от точки о1 с окном w1 к точке о2 с окном w2 на рис. 1 можно из вариационного ряда окна w1 исключить точки столбца 1, отсортировать точки столбца 6 и объединить два полученных вариационных ряда в один. Такой алгоритм работает быстрее по сравнению с независимой сортировкой в каждом окне, однако общее число манипуляций с данными (пусть и менее трудоемких), например хотя бы перебор данных, остается тем же самым, т. е. достаточно большим. Поэтому при медианной фильтрации изображений обычно ограничиваются окнами 3 х 3 или 5 х 5 и редко

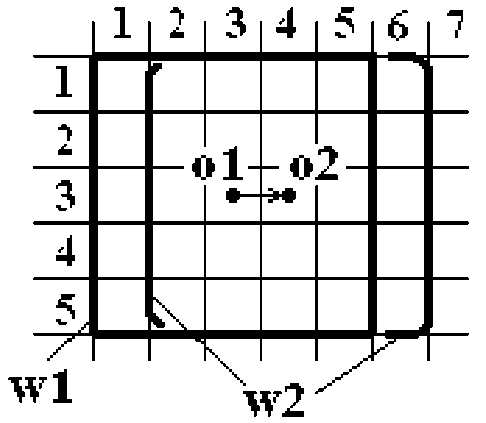
Рис. 1. Сканирование изображения окном медианного фильтра больше, что вполне достаточно, например, для устранения импульсных помех. Такие же ограничения вынужденно принимаются и для различных нелинейных операций морфологической обработки [2], выполняющейся в геометрическом пространстве изображения, и которые в отличие от линейных операций невозможно выполнять в пространстве Фурье.

Вместе с тем существует ряд задач обработки изображений, которые можно было бы эффективно решить при помощи медианного фильтра, но они требуют окна большого размера. Одна из таких задач будет рассмотрена ниже. Поэтому возможное повышение скорости медианной фильтрации сулит большие перспективы в задачах обработки изображений.

БЫСТРАЯ МЕДИАННАЯ ФИЛЬТРАЦИЯ

В работе [3] при рассмотрении ранговых алгоритмов обработки изображений показано, что любую r-ю порядковую статистику vw (r) элемента изображения можно найти из локальной гистограммы hw (q) распределения значений элементов окрестности w (окна на рис. 1), решив уравнение vw(r)

X h w ( q ) = r ^.                    (1)

q = 0

Здесь q = 0, 1, …,Q – 1— номер кванта (бина) гистограммы;

v_w = q_v — квантованное значение видеосигнала;

r = 0, 1, .., S_w -1 — ранг элемента: его номер в вариационном ряду;

S_w — число элементов окрестности (окна) w , или площадь окна в пикселях; в нашем случае S w = n 2 .

Медианный фильтр является частным случаем рангового фильтра с рангом отклика r = ( S w - 1 )/2 . Так как

Q - 1

X h w ( q ) = S w ,                (2)

q = 0

то из (1) следует, что медиана q_m = v_w ( r ) делит площадь гистограммы пополам (за вычетом бина, соответствующего q_m ).

На рис. 2 показано разбиение гистограммы. Здесь S o = h ( q m ) — площадь бина, соответствую-

0                  Ут 6 1

Рис. 2. Гистограмма яркости изображения в окне медианного фильтра щего медиане qm . Остальные обозначения ясны из рисунка. При этом справедливы следующие соотношения:

S l + S o + S h = S w , (3)

S l <  ( S w - 1)/2, (4)

S h < ( S w - 1)/2. (5)

Предполагается, что S_w нечетное. Знаки неравенства в двух последних выражениях могут иметь место только при S o >  1.

При сканировании окном медианного фильтра по строке, при переходе от точки о1 к точке о2 на рис. 1 корректировка гистограммы производится следующим образом.

• 1.    Из гистограммы удаляются данные, соответствующие точкам столбца 1. При этом для каждой точки из площади соответствующего бина вычитается 1.

• 2.    В гистограмму добавляются данные, соответствующие точкам столбца 6. При этом для каждой точки к площади соответствующего бина добавляется 1.

• 3.    В процессе выполнения операций по пунктам 1 и 2 одновременно изменяются величины S L , S H и S o .

• 4.    На оснований выражений (3), (4) и (5) корректируются величины S_L , S_H , S_o и q_m .

Ниже приведен фрагмент программы на языке С, реализующий описанный алгоритм корректировки. Здесь, для удовлетворения синтаксису языка С индексы при S и q заменены строчными буквами, а индексы при h и v упущены. Для случая на рис. 1 n =5 и jo =1.

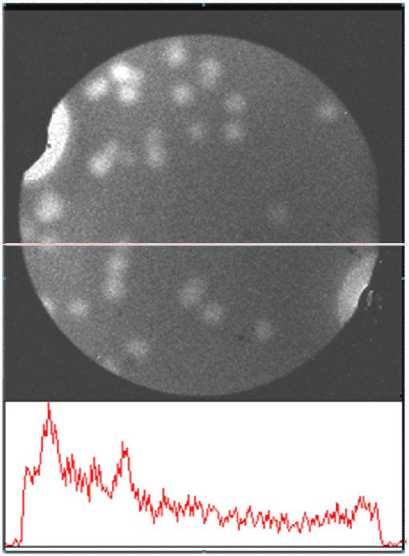
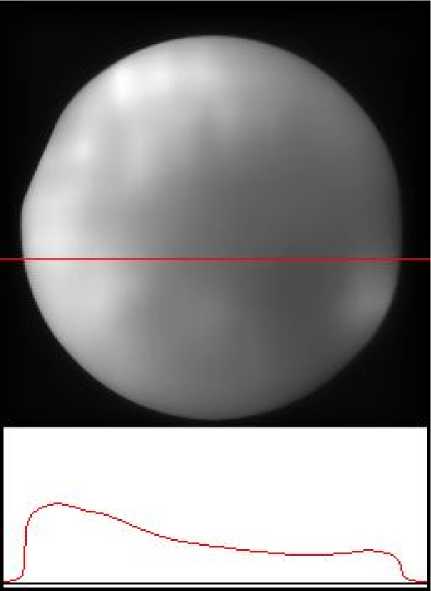
for(i=0; i

{

h[v[jo] [i]] —;

if(v[jo][i] < qm)Sl--;

else if(v[jo] [i] > qm) Sh--;

elseSo--;

h [v[jo+n] [i] ] ++;

if(v[jo+n][i] < qm)Sl++;

else if(v[jo+n][i] > qm) Sh++;

elseSo++;

while(Sl > (Sw-1)/2) { qm--;

if(h[qm] > 0)   { Sl=Sl-h[qm]; Sh=Sh+h[qm+1]; So=Sw-Sl-Sh; }

} while(Sh > (Sw-1)/2) { qm++ ;

if(h[qm] > 0)   { Sh=Sh-h[qm]; Sl=Sl+h[qm-1]; So=Sw-Sl-Sh; }

}

}

Если гистограмма не имеет разрывов, как изображено на рис. 2, величина q_m при корректировке одной точки по п. 4 может измениться не более чем на единицу. Однако реальные локальные гистограммы, как правило, сильно изрезаны. Поэтому корректировки по п. 4 производятся в программе циклами while для пропуска пустых бинов.

Как видно из изложенного выше, рассматриваемый алгоритм медианной фильтрации имеет порядок сложности n, а не n² как это имеет место для наиболее распространенных алгоритмов. Кроме того, здесь не требуется трудоемких операций сортировки.

ПРОВЕРКА РЕЗУЛЬТАТОВ И ВЫВОДЫ

Видеоинформация, содержащаяся в регистрируемых аналитическими приборами изображениях, в частности в изображениях биологических объектов [4, 5], обычно имеет три составляющие: видеоинформация, представляющая исследуемые объекты, шум и фоновая составляющая изображения.

Фоновая составляющая обычно удаляется на начальном этапе обработки изображения, чтобы она не влияла на результаты обработки, или вычисляется с целью учета ее на последующих этапах обработки, что равнозначно. Фон изображения, как правило, изменяется медленнее, чем остальные составляющие сигнала при исследовании локальных объектов. Поэтому обычно [4] фон вы- числяется при помощи линейной низкочастотной фильтрации. Однако если на противоположных сторонах кадра изображения или на границах ра-

Рис. 3. Изображение объектов ПЦР-анализа бочей области изображения величина фона существенно различается (или меняется), то линейный фильтр воспринимает это различие как скачок сигнала и пытается его сгладить. Это — известное явление краевых эффектов. Существуют различные способы борьбы с краевыми эффектами. Чаще всего это или отбрасывание части изображения, затронутого краевыми эффектами, с соответствующей потерей части полезной информации, или расширение кадра с таким заполнением дополнительных полей, чтобы на краях исходного поля изображения, содержащего полезную информацию, не было бы скачков.

Однако, существуют изображения, при обработке которых реализовать такие подходы или невозможно, или очень затруднительно. Так, на рис. 3 показана лунка микрочипа с объектами ПЦР-анализа и профиль сигнала по горизонтальной линии на изображении. На рис. 4 показано вычисление фоновой составляющей при помощи линейной фильтрации, которая, как видно из рисунка, дает большие краевые искажения по контуру лунки. Урезание областей изображения, искаженных краевыми эффектами, в данном случае недопустимо в связи с большой потерей полезной информации, а расширение рабочей области затруднительно из-за того, что эта область является круглой, а также в связи с большой неравномерностью фона по контуру области.

На рис. 5 показано вычисление фона при помощи медианного фильтра. Из рисунка видно, что краевые эффекты в этом случае очень малы, однако при этом потребовалось применение фильтра с большим окном — 41 х 41 пиксель или 1681 пиксель в окне. Размер изображения составлял 256 х 256 пикселей. Измерение времени медианной фильтрации производилось на компьютере со скромными возможностями. Он имел в своем составе одноядерный процессор Pentium^® 4 CPU 2.4 GHz и RAM 512 MB.

Время фильтрации традиционным медианным фильтром с использованием сортировки данных в окне составило 33 с. Время же фильтрации с использованием предлагаемого в настоящей работе алгоритма составило 0.37 с, т. е. почти на два порядка меньше, чем при использовании традиционных алгоритмов. Надо отметить, что, с одной стороны, в рассматриваемой задаче (ПЦР-анализ) время 0.37 с является вполне приемлемым, а с другой стороны, в системах, использующих цифровую обработку изображений, как правило, применяются значительно более мощные компьютеры.

Таким образом, применение предлагаемого алгоритма позволяет значительно ускорить работу медианного фильтра, что, кроме того, позволяет расширить область применения медианной фильтрации.

Рис. 4. Вычисление фона линейным фильтром

Рис. 5. Вычисление фона медианным фильтром