Быстрый алгоритм определения ординат импульсной переходной функции при возбуждении динамического объекта тест-сигналом на основе двоичной м последовательности

Для идентификации линейных динамических объектов используются их различные модели, в том числе и импульсная переходная функция (ИПФ). В этом случае объект может быть описан следующим уравнением:

N - 1

• У ^[ i ^{] -} h 0 +A t • Z h ^[ j ^] • x ^[ i ^- j ^] .        (1)

j = o

Здесь y[i] - реакция объекта, Д t - шаг дискретизации, x[i] – входной тест-сигнал, h[j] – ординаты импульсной переходной функции, h₀ – реакция объекта на постоянный рабочий сигнал, N – время памяти объекта [1].

На практике для независимой оценки ординат ИПФ при идентификации применяют ортогональные к сдвигу кусочно-постоянные тест-сигналы небольшой амплитуды, не нарушающие нормальное функционирование объекта, тогда при измерении реакции объекта один раз на такте тест-сигнала:

p

Z У ^[ i ^] • x ^[ i ^- j ^]

h[ j ] - ~_p----------.         (2)

Z x ²[ i - j ]

i = 0

В качестве тест-сигнала удобно использовать легко реализуемые псевдослучайные двоичные М-последовательности [1, 2]. Определение вза-имокорреляционной функции для различных j по (2) требует большого объема вычислений.

Известен алгоритм, уменьшающий объем вычислений для определения ординат ИПФ при возбуждении динамического объекта тест-сигна-лом в виде двоичной М-последовательности, на

основе быстрого преобразования Адамара [3, 4, 5]. Целью этой работы является модернизация быстрого алгоритма для вычисления ординат ИПФ.

Двоичная М-последовательность является упорядоченным с помощью сопровождающей матрицы (характеристического полинома F(x)), множеством компонент Si вектора координат элементов поля Галуа GF(2n) в степенном базисе [6]. М-последовательность, генерируемая с помощью характеристического полинома степени n, имеет период Р = (2n – 1) тактов.

При генерации тест-сигналов эти компоненты заменяются реальными сигналами с нормированными значениями:

х(0) = +1; х(1) = -1. (3)

Умножение для реальных сигналов оказывается эквивалентным сложению по модулю 2 для компонент S:

i

1 ф o - 1 ^ ( - 1) • ( + 1) = - 1

• 1    ф 1 - o о ( - 1) • ( - 1) -+ 1

0 ф 0 - 0 >  ( + 1) • ( + 1) -+ 1 (4) 0 ф 1 - 1 >  ( + 1) • ( - 1) -- 1

В тест-сигнал на основе двоичной М-после-довательности вводятся дополнительные такты для получения несмещенной оценки h[j] (“нулевая строка”), а также для устранения погрешности от неверного задания исходного состояния объекта перед началом тестирования [1, 2].

Для упрощения изложения алгоритм вычисления ординат ИПФ далее рассматривается для небольшого количества h[j]. На рис. 1 приведен тест-сигнал на основе двоичной М-последова-тельности с характеристическим полиномом F(x) = х3+х+1 и периодом 7 тактов, точками указаны моменты измерения реакции объекта.

На практике используются М-последова-тельности с характеристическими полиномами степенью не менее 8.

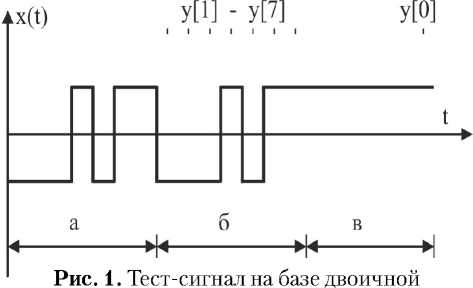
М-последовательности.

а – формирование начальных условий, б – период М-последовательности, формирование “нулевой строки”.

линейных динамических объектов. Например, в пятой строке матрицы Х приведен тест-сигнал с запаздыванием на 4 такта по отношению к входному сигналу генератора М-последовательности. Вычислим коэффициенты полинома-остатка по (9) для этого случая:

R 4 - x ⁴ mod( x ³ + x + 1) - ( x ² + x ) , т.к.

x x + x

—3-------- x +—з-------.

x + x +1 x + x + 1

Из (10) следует, что a₁ = 1, a₂ = 1, a₃ = 0 и x [ i - 3] - x [ i ] • x [ i - 1] .

Двоичная запись матрицы Х2 имеет вид:

В соответствии с (2):

0		4 + + + + + + + +^	4 У [0] )
40]		+---+-++		y [1]
41]	1 - — •	++---+-+		y [2]
h[2]		+++---+-	•	y [3]
h [3]	8	+-++---+		y [4]	(5)
h [4]		++-++---		y [5]
h [5]		+-+-++--		y [6]
( h [6] j		v +-- + - + + - j		l У [7] J

^X 2 ^-

4 ^00000000 ) 01110100 00111010 00011101 01001110 00100111 01010011

( 01101001 J

.

В (12) представлены матрица Уолша-Адама ра [7] W и ее двоичный аналог W₂ размернос тью 8 • 8 .

-

H - —— X • Y

P + 1         ^.

Здесь H и Y – векторы-столбцы оценок ординат ИПФ и реакции объекта, X - задержанные реплики входного сигнала, матрица плана эксперимента. С целью упрощения записи в матрице Х приведены только знаки нормированных значений тест-сигнала, дополнительная “нулевая строка” размещена в левом столбце Х.

В аппаратном или программном генераторе непосредственно доступны М-последователь-ность и ее реплики с запаздыванием от 1 до (n-1) такта. М-последовательности с запаздыванием j > n являются линейными комбинациями последовательностей с запаздываниями меньше n того же характеристического полинома:

S. _ j = a_x • S ® a 2 • S , . , ©•......® a n • S - n + 1 . (7)

Для тест-сигналов выражение (7) записывается так:

x [ i - j ] - ( x [ i ]) a ¹ • ( x [ i - 1]) a ² • • ( x [ i - n + 1]) a n (8)

Коэффициенты ai в (7, 8) совпадают с коэффициентами полинома-остатка Rj(x) в GF(2n) [6]:

R j ( x ) - x^J mod F ( x ) .         (9)

Выражение (9) иногда называют алгоритмом Дэвиса, его применяют для генерации задержанных М-последовательностей при идентификации

	4 ++++++++)		4 00000000 )
	+-+-+-+-		01010101
	++--++--		00110011
W -	+-+--+-+ ++++----	, W -	01011010 00001111	. (12)
	+--+-++-		01101001
	+--++--+		01100110
	v ++----++ j		l 00111100 ;

При умножении вектора-столбца на матрицу Уолша-Адамара используют эффективное быстрое преобразование Уолша-Адамара (БПУ), значительно уменьшающее объем вычислений [7].

Согласно (7) любая строка матрицы Х2 является линейной комбинацией по модулю 2 n строк, соответствующих последовательной смене n-разрядных двоичных чисел в генераторе М-последовательности. В Х2 это вторая, третья и четвертая строки. Для тест-сигналов в Х этот алгоритм трансформируется в (8).

В матрице Уолша-Адамара размерностью 2 ⁿ • 2 ⁿ строки также определяются линейной комбинацией по модулю 2 n строк, соответствующих последовательному возрастанию двоичных n-разрядных чисел, образованными пересечением столбца и этими строками. Верхний (второй) элемент столбца соответствует младшему разряду.

В [3, 4] предложена методика применения БПУ для вычисления оценок ординат ИПФ при возбуждении динамического объекта тест-сигна-лом на основе М-последовательности.

В матрице Х2 столбцы упорядочены в порядке появления двоичных n-разрядных чисел в генераторе М-последовательности. После перестановки столбцов в порядке возрастания двоичных n-разрядных чисел матрица Х2совпадет с W2 (соответственно Х с W). Чтобы результат умножения матрицы на вектор-столбец не изменился, следует переставлять и компоненты y[i] вектора Y и спектральные коэффициенты Уолша, порядок следования которых отличается от расположения элементов h[j] в векторе H. Таким образом:

H - A 2 • W • A 1 • Y . (13)

Здесь А1 и А2 – матрицы перестановок, определяемые характеристическим полиномом М-последовательности.

Для перестановки элементов в векторе Y достаточно записывать замеры реакции объекта y[i] в массив не в естественном порядке, а по адресам, задаваемым двоичными числами в генераторе М-последовательности. Например, из (5) и (11) следует, что в векторе Y элементы должны быть переписаны в следующем порядке: y[0], y[1], y[6], y[2], y[7], y[5], y[4], y[3], матрица А1 тогда имеет вид:

	< 10000000 ^
	01000000
	00000010
	00100000
A -	00000001	.           (14)
	00000100
	00001000
	( 00010000 ;

Разумно применить алгоритм БПУ на осно- ве факторизации матрицы преобразования Уол-ша-Адамара на произведение n одинаковых матриц. В отличие от алгоритма типа “бабочка” [7] в этом случае в каждом из n этапов БПУ выполняется одна и та же процедура, что упрощает программную реализацию алгоритма.

На рис. 2 алгоритм БПУ изображен в виде графа для рассматриваемого примера. Спектральные коэффициенты, вычисленные с помощью БПУ упорядочены по возрастанию номеров функций Уолша.

В [3, 4] показано, что адреса в двоичном формате, по которым расположены оценки ординат ИПФ h[j] в векторе спектральных коэффициентов Уолша, могут быть определены из матрицы К размерностью n • 2 ” . В матрицу К отбираются n столбцов из Х₂, так чтобы верхние строки матрицы К, начиная со второй, образовали единичную матрицу размерностью n • n . Младший бит адреса располагается в левом столбце.

Для случая F(x) = х3+х+1 матрица К и матрица перестановок А2 на ее основе имеют вид:

K -	< 000 ^ 100 010 001 110	, A 2 -	< 10000000 ^ 01000000 00100000 00001000 00010000	.      (15)
	011		00000010
	111		00000001
	L 101 >		( 00000100 2

Соответствие спектральных коэффициентов Уолша и ординат ИПФ указано и на рис. 2.

Недостатком рассмотренного быстрого алгоритма является необходимость генерации в процессе вычислений всей матрицы Х₂ размерностью 2 ” • 2 ” , например, при n = 8 это уже 65536 элементов.

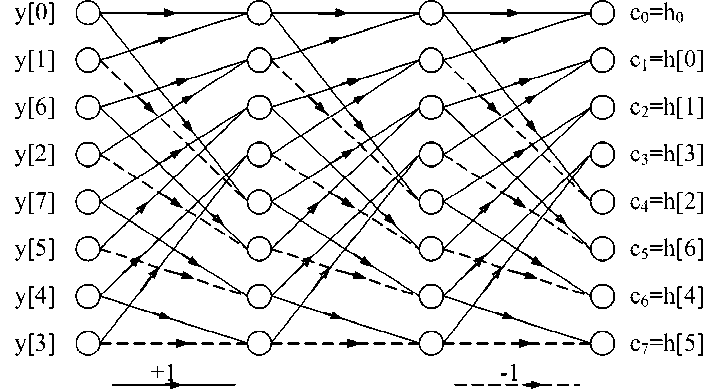
Рис. 2. Алгоритм БПУ

В этой статье предлагается другой способ сопоставления ординат ИПФ h[j] со спектральными коэффициентами Уолша в БПУ.

Спектральные коэффициенты, полученные в результате применения БПУ (Рис 2), расположены по возрастанию номеров функций Уолша при их естественном упорядочивании (по Адамару) [7].

Полная ортонормированная система 2ⁿ функций Уолша (Рис.3) определяется на основе n функций Радамахера R_i(t) [7]. Функции Уолша определяются через произведение функций Ра-дамахера. Наличие или отсутствие j-й функции Радамахера при получении i-й функции Уолша определяется j-м разрядом двоичного представления числа i. Например, w₁(t) = w₀₀₁(t) = R₁(t), w 5 ^(t) = w 101 ^(t) = ^R 1 ⁽ t ) ' ^R 3 ⁽ t ) и т.Д.

Матрицы Х (5) и W (12) отличаются только перестановкой столбцов, следовательно строка x[i] в (5) соответствует R₁(t) в (12), строка x [ i ] • x [ i - 1] в (5) соответствует R 1 ( t ) • R ₂( t ) = w₀₁₁(t) = w₃(t) в (12) и т.д.

Таким образом, двоичная запись номера спектрального коэффициента Уолша с_i указывает сигналы с каких разрядов генератора М-пос-ледовательности использовались при его вычислении. Адреса, по которым находятся оценки ординат ИПФ h[j] в векторе спектральных коэффициентов Уолша определяются так: h₀ = c₀ и h[j] = c_k , k = 2^j при jj > n . Необходимости генерировать всю матрицу Х при таком алгоритме не возникает.

Процесс идентификации связан с автоматическим управлением объектом исследования, оборудованием для подачи тест-сигнала и сбора данных, обработкой данных. Это удобно осуществлять в специализированной среде программирования LabVIEW [8]. Разумно и подготовительную работу делать в той же среде. Автором был разработан несложный виртуальный прибор для определения ординат ИПФ h[j] линейного динамического объекта при его возбуждении тест-

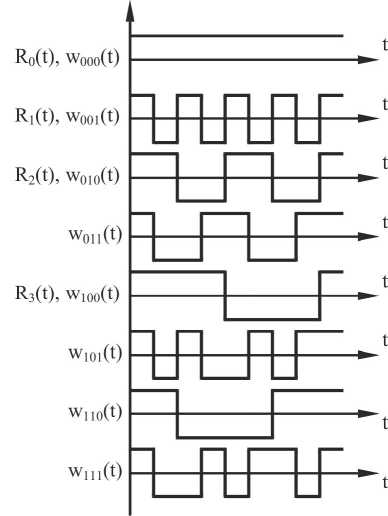
Рис. 3. Функции Уолша, упорядоченные по Адамару сигналом на основе двоичной М-последователь-ности. На рис. 4 приведен фрагмент лицевой панели виртуального прибора, на рис. 5 часть блок-схемы.

В разработанном виртуальном приборе динамический объект моделировался набором ординат ИПФ (100, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 12). На рисунке 4 представлено состояние лицевой панели виртуального прибора после проведения идентификации. Использовалась М-пос-ледовательность с характеристическим полиномом х8 + х6 + х5 + х4 + 1, который задан в двоичной форме. Ординаты ИПФ полностью восстановлены, указаны их адреса в массиве спектральных коэффициентов Уолша.

ВЫВОДЫ

При вычислении оценок ординат ИПФ линейных динамических объектов при возбужде-

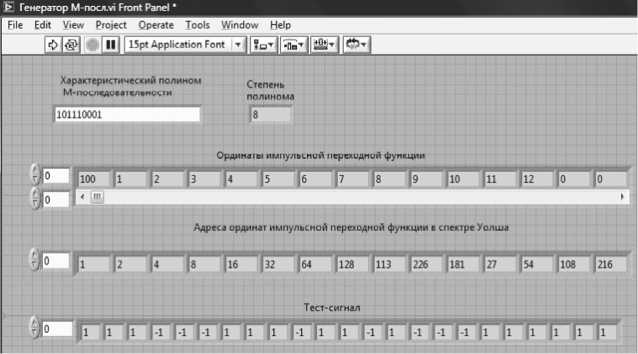
Рис. 4. Лицевая панель виртуального прибора

Рис. 5. Часть блок-схемы виртуального прибора

нии их тест-сигналом на основе двоичных М-последовательностей используется эффективный алгоритм быстрого преобразования Уолша-Адамара. При этом необходимо в зависимости от вида характеристического полинома М-последо-вати произвести перестановки компонентов в векторах реакции объекта и спектральных коэффициентов Уолша. В статье предложен более простой алгоритм определения соответствия между оценками ординат ИПФ и спектральными коэффициентами, полученными в результате БПУ, не требующий генерации всего плана эксперимента размерностью 2 n • 2 n .