Быстрый алгоритм расчета интегралов специального вида

В работах [1, 2] было показано, что проблема нахождения функции отклика оптикоэлектронного датчика с учетом дифракционных поправок сводится к задаче вычисления интегралов специального вида A_s ( p , q ) и A_c ( p , q ).

1 _dt

A s ( p , q ) = J—sin pt )co^s( qt ),                 (1)

0 ^t

A c ( p , q ) = J 0

Как показал последующий анализ, интегралы (1), (2) в общем случае не могут быть представлены в виде комбинации конечного числа элементарных и/или специальных функций. С формальной точки зрения численные значения интегралов специального вида A_s ( p , q ) и A_c ( p , q ) могут быть найдены на основе общеизвестных квадратурных формул. Однако фактически, вычисление этих интегралов по квадратурным формулам Симпсона, Гаусса и т. п. оправдано только при небольших значениях аргументов p и q .

В тех случаях, когда выполняются условия p » 1 и/или q » 1, подынтегральные выражения в формулах (1), (2) становятся быстроосциллирую-щими, и использование квадратурных формул для вычисления величин A_s ( p , q ) и A_c ( p , q ) становится некорректным, т. к. погрешность вычисления быстро растет с увеличением p и/или q .

В конечном счете, задача корректного расчета величин A_s ( p , q ) и A_c ( p , q ) численными методами сводится к необходимости избавиться от сложения большого числа знакопеременных слагаемых, имеющих одинаковый порядок величины. С точки зрения теории аналитических функций, общий подход к преодолению указанной проблемы основан на использовании идеи метода перевала [3]. Однако технически эта идея может быть реализована несколькими способами. А для использования датчиковой аппаратуры в реальном масштабе времени необходимы быстрые и устойчивые алгоритмы обработки сигналов, т. е., функции отклика.

В настоящей работе проделано сопоставление вычислительной эффективности различных алго-

^dt cos( pt ²) sin( qt ) . t

ритмов расчета интегралов (1), (2) с целью выявления наиболее быстрого и устойчивого из них.

Хорошо известно, что абсолютное большинство «физических» функций (а интегралы (1) и (2) относятся к таковым) при малых значениях аргумента вычисляются посредством разложения в степенной ряд, при больших значениях аргумента – в асимптотический ряд, а при промежуточных значениях аргумента наиболее эффективны различные аппроксимации. Поэтому каждая комбинация параметров p и q требует отдельного рассмотрения. В соответствии с этим, описание алгоритмов вычисления аналитических функций двух аргументов A_s ( p , q ) и A_c ( p , q ) при различном соотношении величин p и q выделено в отдельные параграфы.

1. Случай p « 1 и q « 1

В соответствии с общей идеологией численных методов в этом случае алгоритм расчета интегралов специального вида строится на основе степенных рядов.

Очевидно, что подынтегральные выражения в формулах (1) и (2) имеют хорошие аналитические свойства, и в соответствии с этим величина A_s ( p , q ) может быть представлена в виде:

A s ( p , q ) ⁼ j— sin( pt ² )cos( qt ) =

0 ^t

да

=z

n =0

( - 1) ⁿq ^{2 n} (2 n )!

J sin( pt 2 ) t ^{2 n - 1} dt.

Произведем замену переменных x = t ². В результате приходим к выражению:

A s ⁽ p , q ) = 2Si⁽ p ) +

1 ” ( - 1) ⁿ Л2 n 1

+7Z/ _{n M} J^sin( p^x ) x n ^{dx ,}

2 n =1    (2n ^)!    0

где Si ( z ) – интегральный синус, а интеграл в формуле (4) является табличным

J sin( px ) x^{n - 1} dx =

да z k =0

( - 1) k p 2 k ^{+ 1}

( n + 2 k + 1)(2 k + 1)! .

Из (3) и (5) следует, что интеграл A_s ( p , q ) может быть представлен в виде двойного степенного ряда:

A s ⁽ p , q ) =

₌ 1 у ( - 1) n q ² n у     ( - 1) k p ^{2 k + 1}

= 2 ^ (2 n )!   ^E ( n + 2 k + 1)(2 k + 1)!

= |si⁽ p ) +

+ £ у ( - 1) n q ^{2 n} у     ( - 1) ^kp ^{2 k + 1}

⁺ 2 ^E (2 n )!   ^E ( n + 2 k + 1)(2 k + 1)!'

ления в виде быстро сходящихся рядов. Воспользуемся для этого методами теории аналитических функций и рассмотрим первый из анализируемых интегралов.

Представим выражение для интеграла A s ( p , q ) в следующем виде:

Совершенно аналогично вычисляется интеграл

1 dt 2

A s ⁽ p , q ) ⁼ Re j—^sin( pt ^)exP⁽ iqt ) = _ 0 t                             _

A c ⁽ p , q )^:

= Re

A c ⁽ p , q ) =

₌ у ( - 1) n q ^{2 n + 1} у      ( - 1) k p ^{2 k}

"^E (2 n + 1)! ^E (4 k + 2 n + 1)(2 k )!

ГП"  ^f /2 p )

=q^C a_ + у 2 p ^ V n J у (-1)nq2n+1 у     (-1)kp2k

'^E (2 n + 1)! ^E (4 k + 2 n + 1)(2 k )!'

да

: i n ^{(2 n} + ¹⁾ j n ⁽ q ) ф n ⁽ p )

. n =0

При переходе от (1) к (3) мы воспользовались соотношениями [4]:

cos( yt ) = Re ( exp( iyt ) ) .                            (9)

да exp( iyt)=e in(2 n+1) jn(y) Pn(t).                (10)

n =0

В формулах (6) и (7) в явном виде выделены главные (нулевые) члены разложения, для которых имеются стандартные алгоритмы расчета.

Очевидно, что и внешний и внутренний ряды в формулах (6) и (7) имеют мажоранты, и, следовательно, являются сходящимися. Скорость сходимости этих рядов не хуже, чем у мажорирующих рядов, определяющих тригонометрические функции sin( x ) и cos( x ). Однако необходимость суммирования внутреннего ряда для расчетов коэффициентов при каждом члена внешнего ряда существенно замедляет процесс вычисления.

Из (8) легко видеть, что

да

A s ⁽ p , q ) = E ^{( - 1) n (4 n + 1)} j 2 n ⁽ q ) Ф 2 n ⁽ p ),        ⁽¹¹

n =0

где

Ф2n (p) = fdt sin(pt2)P2n (t) = 0 t да ( 14^ м2k+1 1

= у ^{( - 1) p} [dt . t ⁴ k ^{+ 1} . P ( t ).

£0(2 k + 1)! ^{j             2} n

Содержащийся в формуле (12) интеграл является табличным [4, 5]

j dt . t ^{4 k + 1} . P 2 n ( t ) =

_ ( - 1) ⁿ Г ( n - 2 k - 1/2) Г (2 k + 1)

= 2 Г ( - 2 k - 1/2) Г ( n + 2 k + 2) ,

откуда вытекает окончательное выражение для ко- эффициентов разложения (12):

1    „ (- 1) k p ² k + ¹

Ф 2 Ap  2 ^{n + 1 E} 2 k + 1

(4 k + 1) n

( n + 2 k + 1)!

где ( a ) _n - символ Похгаммера (см. Приложение).

Совершенно аналогично вычисляется интеграл A c ( p , q ):

да

A c ⁽ p , q ) = E ^{( - 1) n (4} n + ³⁾ ■ j 2 n +1 ⁽ q ) ■ Ф 2 n +1 ⁽ p ), ⁽¹⁵⁾

n =0

где

Коэффициент ф _{2 n + 1}( p ) также выражается через табличный интеграл [4, 5]:

d ”	exp( ip ) - 1
д ( ip ) ”	ip

j dt ■ t ⁴ k '

( 2 к - 1 )

n

² ” ^{+ 1()} 2 ( 2 к + 1/2 ) n _{+ 1}"

d ” d ( ip ) ⁿ

Г e x            d ” ( ip )

l e^xp⁽ ip ) ■ ⁽ ip )

^{L                 J}    d( ip )

Таким образом, окончательное выражение для коэффициентов ф _{2 n + 1}( p ) имеет вид:

откуда следует, что:

1 ю / 1\ к „2 к t \ - ¹ V ^{( - 1)} Р ^Ф 2 ” ^{+ 1} p "2 § (2 к )!

( ^{2 к} — 1 ) n

( ^{2 к} + ^1/2 ) n +1 '

д n	exp( ip ) - 1
д ( ip ) n	ip

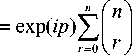
d r ( ip ' d ( ip ) r

d ” ( ip ) ^{- 1} d ( ip ) ⁿ

Соотношения (11), (14), (15) и (18) полностью решают задачу вычисления интегралов (1), (2) в случае умеренных значений аргумента p <  5 при произвольных значениях аргумента q . В дополнение к сказанному отметим, что ряды (11) и (15) сходятся быстро, а сферические функции Бесселя вычисляются с помощью вычислительно эффективного и устойчивого алгоритма, построенного и исследованного в работах [6, 7, 8].

и, таким образом:

д ”    exp( ip ) - 1

d ( ip ) ” _ ip

X

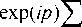
к =0

= ( - 1) ” n !( ip ) ” ^{+ 1)} x

( - 1) ^к ( ip ) ^к к !

4. Случай умеренных q <  5 и произвольных p >  5

Конечная сумма, фигурирующая в квадратных скобках в формуле (24) есть не что иное, как частичная сумма ряда Тейлора для экспоненты (см. Приложение):

Описанный в предыдущем разделе алгоритм представляется весьма изящным, однако ряды (11) и (15) имеют достаточно сложную структуру коэффициентов разложения и содержат специальные функции математической физики (сферические функции Бесселя). Все вышесказанное ориентирует на поиск гибридных алгоритмов, в рамках которых изначально выделены «главные члены» разложения интегралов специального вида A s ( p , q ) и A c ( p , q ) по той или иной комбинации параметров.

Из соотношения (4) следует, что

д ”    exp( ip ) - 1 =

д ( ip ) ” _      ip _

= ^{( - 1)} ” ” ^!( ip ^{) - (} ” ^{+ 1)} [ ^exp⁽ ip ) ■ e n ^{( -} ip ) ^{- 1}.

Учитывая это обстоятельство, преобразуем выражение для A s ( p , q ) к следующему виду:

. , х 1 х q ² COS p A s ⁽ p , q ) = - A^Si( p ) ⁺——⁺ 2 [         2 p

+ Im [ S ( p , q ) - exp( ip ) x

A s ⁽ p , q ) = 2Si⁽ p ) ⁺

-П ” o² ”    1

+ - § ⁽ ) q - Imjexp( ipx ) x ” ¹ dx .

2 n =1 (2 n )!       ^J₀

Ю x § n =1

n ! q ² ” ^{+ 2}( ip ) ^{- (} ” ^{+ 1)} (2 n + 2)!

■ e n ( ^- ip )

.

где

s ( p , q )

У n ! q'^{n <}( /p ) ” ■"

§    (2 n + 2)!

Выражение (19) удобно представить в виде:

A s ⁽ p , q ) = 2Si⁽ p ) ⁺

Для того чтобы выразить мнимую часть степенного ряда в формуле (27)

1 ” ( - 1) ” л²”         д ^{n 1} i.                  ’

+ — V------- Im------- f exp( ipx ) dx

2 § (2 n )!       d ( ip ) ” ' ^j

S Im ⁽ p , q ) = ^Im { S ⁽ p , q ) } ,                        ⁽²⁸⁾

через специальные функции математической физики, поступим следующим образом. Перепишем (28) в виде:

Откуда немедленно следует, что 1            q ²

As(p, q) = 2Si( p)- уx x Im If (-1)”q2” d” Г exp(ip) -1 [”T^(2n + 2)! d(ip)” _     ip

Ю

SIm (p, q) = -§ к=0

(2 к )!( - 1) ^к (4 к + 2)!

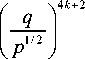
Введем переменную z = q ■ p ^1/2 и исследуем свойства функции:

Производная n - го порядка в (21) вычисляется элементарно:

ю

SIm(1, z) =-§ к=0

(2 к )!( - 1) ^к (4 к + 2)!

4 к + 2 z

Из (30) видно, что dS,m (1, z) =_у (2k)!(-1)k z4k+1 dz Ь (4k +1)! Z

I z ² J

= —J^{n U} 1/2 I у,⁰ I ,

(2 n + 1)! = Г (2( n + 1)) =

= (2 n ) ^{- 1/2}2^{2 n + 3/2} Г ( n + 1) Г ( n + 3/2).

Отсюда следует, что

A c ⁽ p , q ) = ? ^х

2 V n

где U _v ( z , £ ) - функция Ломмеля двух переменных (см. Приложение). Таким образом, получаем:

^S ,m ^(1, z ) = ^- z^^х

/ _o \ n +1/2

х Re у ^{( - 1) n} Y ^{( n + 1/2} ip ) I q_ 3

n Z0    n ! Г ( n + 3/2) 1 4 ip J

.

Из теории гамма-функций известно также, что

х lim

^0

to z k =0

/ ix k ( 2

^{( - 1)} I ^z

4 k + 2 1 2 z

J 2 k +1/2

Y ( n + 1/2, z ²) Г ( n + 1/2)

erf ^{( z} ) ^-

Существует и другой способ нахождения функции S ( p , q ). Для того чтобы просуммировать исследуемый ряд (27), воспользуемся соотношением:

n

—1= exp( - z X^

N П            k =1

H 2 k -1 ( z )

( n - k )!(2 k )!^.

Принимая во внимание соотношение (41), мы

E k ^!    Ik 1 х/л ¹ x ³ _с( x

----x = 1 +--x exp — erf — k=0(2k)!           2      P( 4 J 12,

приходим к выражению:

и проинтегрируем его в пределах от 0 до z . В ре

зультате, мы приходим к соотношению:

A c ⁽ p , q ) =

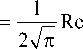
/   4 \ n +1/2

”     ( П n    ( л2 )

у   (-1)     I q I n=0 n!(n +1/2) 14 ip J

z ”

[У — x ^{2 k}dx = ^{J Z} (2 k )!

х

=J1

0 _

. х/л      ¹ x ²³ J X

+-- x exp — erf —

2      | 4 JI 2

из которого вытекает, что:

у ^{k !}    x 2 k +1

k z0(2 k + 1)!

и, таким образом:

2      2

erf( z ) — _re ^{- z}

n

n

z

Hlk 1( z )    ³

2 k 1

( n - k )!(2 k )! _?

■ dx ,

г- I x ² ) I x 3 n exp — erf — ,

I 4 J 12 J

” Н              ^z.       I v2 3

У---- ^:— z ^{2 k +} = Vn [ dx exp — erf — . (36)

Z(2k + 2)! J У 4 J 12J

Выражение (36) можно также представить, как

у ^{k !}    z 2 k +2

k z 0 (2 k + 2)!^Z

z /2

= л^ erfi ( z /2 ) ^ erf ( z /2 ) - 4 J dy ■ F ( y )

где F ( z ) - интеграл Досона (см. Приложение).

Вычислим интеграл A c ( p , q ) для исследуемого случая умеренных q <  5 и произвольных p >  5 . С учетом проделанных выше вычислений легко показать, что:

A c ⁽ p , q ) =

= ¹Re

to z n =0

( - 1) n

(2 n + 1)!

2 \ n +1/2

q-1 ip J

Y ( n + 1/2, ip )

Воспользуемся известным свойством гамма-функций:

Соотношение (42) допускает существенное упрощение. Для этого представим его в следующем виде:

A c ⁽ p , q ) = 2т п ^Re ^^S 1 ⁽ p , q ^)erf( ^p ) ]^-

- Irc [s2( p, q )e-p ],

П

где через 2 ₁ обозначена следующая сумма (см. [5]):

to

^1(p, q) = Z n=0

( - 1) ⁿ n !( n + 1/2)

2 x n +1/2

q- 1

4 ip J

= Y

1, q! 3 .

2 4 ip J

Вторая сумма, обозначенная через S ₂, входящая в формулу (43):

to

М p , q ) = :

n =0

( - 1) n n !( n + 1/2)

2 x n +1/2

q3

4 ip J

_х у H 2 k -1 СУ ^ip ) fzK n - k )!(2 k )!’

вычисляется несколько сложнее.

Хорошо известно, что гамма-функция целого отрицательного аргумента обращается в бесконечность. Учитывая это обстоятельство, преобразуем (45):

^ 2 ⁽ p , q ) =

у    ( - 1) n   I q ² 3 n ^{+ 1/2} у H 2 k -1 (T ip )      ⁽⁴⁶⁾

n : 1 n !( n + 1/2) 1 4 ip J      k : 1 ( n - k )!(2 k )!^.

В результате указанного преобразования мы можем изменить порядок суммирования по индексам к и n :

гласно [5], искомые интегралы вычисляются точно.

Согласно [5] интеграл A s ( p , q ) равен

A s ⁽ р , q ) *

=2( Р, q ) = 1    . х к=1     (2 k )!

да х1

n =1

( - 1) )

n !( n - к )!( n + 1/2)

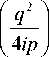
n +1/2

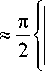
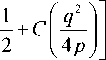
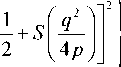
В рассматриваемом приближении интеграл

Из (47) вытекает, что

A c ( p , q ) также сводится к табличному:

^ 2 ⁽ p , q ) =

да

= 1

к =1

( - 1) ^кн 2 к -1 ( y ip ) (2 к )!

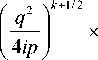
A c ⁽ Р , q ) »|^Re

i п „ erf e 4 —

I   2^ Р

.

да            ( п™             л2 ^т у__________(-1)___________I q I т=0 т!(т + к)!(т + к +1/2) ( 4 ip J

Аналитические свойства интеграла ошибок позволяют свести выражение (52) к линейной комбинации интегралов Френеля:

Внутренняя сумма в формуле (48) выражается через интеграл от функции Бесселя. В результате получается выражение для Х ₂:

i П   л erf [ e

у р , ^ ) = 1 ^‘H" —'⁽У⁾ _;< ( t ) dt.   (49)

к =1       ^{2 (2} к ^)!        0

В заключение отметим, что сумма 2 2 может быть представлена в виде:

^⁽ p , q ) =

+   ( - 1) ^к г ( к + 1/2) н 2 к -1 ( ^Р )

=Т¹       да ^х •    ⁽⁵⁰⁾

^х { z [ ^Jk ⁽ z ) H к -1 ⁽ z ) ^{- J}k -1 ⁽ z ) H к ⁽ z ) ] } z = JL , ip

. у[2лр,

q

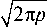
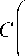
- S

Д 2 п р J   ^ У2л р J

Откуда немедленно получается окончательное выражение для интеграла A c ( p , q ) в приближении q » p » 1:

A c ⁽ р , q ) = П ■

C

q

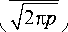
+ S

( л

(У2л p J

где H _к ( z ) - функция Струве.

Полученные соотношения позволяют вычислять искомые интегралы со степенью точности, достаточной для практических расчетов в системах, работающих в реальном времени.

5. Случай больших значений аргументов q » p » 1

В случае очень больших значений обоих аргументов q » p » 1 оценка исследуемых интегралов становится тривиальной. При этом наибольший интерес представляет случай экстремально больших ( p >  50) значений аргумента p , поскольку описанный выше алгоритм для случая умеренных p <  5 и произвольных q >  5 на практике пригоден вплоть до значений аргумента p ~ 50 .

В рассматриваемом случае q » p » 1 зависимость величины интеграла от верхнего предела интегрирования становится несущественной. Другими словами, мы можем распространить пределы интегрирования в (1) и (2) до бесконечности. Тогда, со

пригодное для вычислений в реальном масштабе времени.

6. Случай больших значений аргументов p » q » 1

Если для аргументов p и q выполняется соотношение p ^ q ^ 1, то интегралы A s ( p , q ) и A c ( p , q ) можно вычислить методом перевала. Покажем, что это действительно так. Для этого заметим, что

A s ⁽ р , q ) =

= 1Im J dt [ e ^{i ( pt 2 +} qt ^{) - ln} t + e ^{i ( pt} 2 ^- qt ^{) - ln} t

2 0 ^L

В соответствии с основной идеей метода перевала, разложим показатели экспонент в формуле (55) в ряд Тейлора в окрестности 1 ₀:

i ( pt ² ± qt ) - ln t « i ( pt 2 ± qt ₀) -

.        11,.     1 L      ,2

^{- ln} t 0 ⁺t| ² i ^{p +} ~ I ⁽ t ^- t 0 ) . 2 t

Стационарная точка 1 ₀ удовлетворяет уравнению

i (2 pt 0 ± q ) ^- — = 0, t ₀

имеющему очевидное решение

t o ( ± q ) = + q- ±

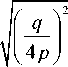
i 2 p ^,

которое мы будем записывать как

t o ( ± q ) = + q- ±Vp exp( i Ф /2),                (59)

4 p

где

<

I q i I ¹ i p = J — I +I — I

V 1 4 p ) l ² p )

,

. I 8 P Ф = - arctan I —v l q

.

В рамках поставленной задачи выполняются условия p >  0 и q >  0. В этом случае стационарная

точка t ₀ расположена далеко от исходного контура интегрирования t е [ 0,1 ] , проходящего по вещественной оси. Поэтому первое слагаемое в формуле (55) с «перевальной» степенью точности не дает вклада в величину A_s ( p , q ), а интеграл от второго слагаемого вычисляется элементарно.

¹        ( i ( pt ² - qt )-ln t )

I dt e'             '

^{2 n} _e i ( pt 02 - qt 0 )

t ₀

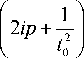
-1/2

По аналогичной причине из двух корней уравнения (58) в «перевальном» выражении для искомой величины A_s ( p , q ) следует удержать лишь тот, для которого выполняется условие Re( t ₀) >  0 . Тогда в рамках мето-

да перевала мы приходим к следующему выражению

A ( p , q ) ® — Im J" dt exp ( i ( pt ² - qt ) - In t ) »

“^Im

e i ^[ pt 2 (- q )- qt o ( - q ) ^] t o^{( -} q )

^[- ( ² ip ⁺ 1 - ²( - q ) ) ]     > ,

и в результате очевидных преобразований мы получаем

A s ⁽ p , q ) =

‘^Re

exp [ i ( pt 02 ( - q ) - qt 0 ( - q ) ) ] 4 ² ipt 0 ^{2( -} q ) ^{+ 1}

При извлечении корня из (-1) при переходе от формулы (62) к формуле (63) лист римановой поверхности (знак + или - ) выбирается из условия,

что в рассматриваемом случае p » q » 1 стационарная точка 1 ₀ » 0 , и, следовательно, A s ( p , q ) >  0.

Учитывая, что согласно (58) qt0 = 2pt2 + i, при ведем выражение (63) к виду

A s

^exP ( ^- ipt о( - q ) )

откуда получается окончательная формула для вычисления интеграла A_s ( p , q ) методом перевала

A s ( p , q ) = + E ■ e ■ Re { e - ipt 2 ^{( -} q ) - ^{i ф 1 /2} ) , \ 2Pi          ⁽                 ’

где

I q pt0 (-q) = p I T- + Vp exp(1 ф / 2) I l4 p              J

—- + q TP exp( i ф /2) + P exp( i ф ), 16 p 2

а модуль и фаза подкоренного выражения в знаменателе формулы (64) определяются соотношением

P i exp( i Ф 1 ) ⁼ 2 ipt 02 ( - q ) + 1.

Перейдем к рассмотрению интеграла A_c ( p , q ) в приближении перевала:

A c ( p , q ) = 1lm | dt [ e ^{i ( pt 2 +} qt ) - e ^{i ( pt 2} - qt ) ] t "' .       (68)

Легко видеть, что в этом приближении выполняется соотношение

A c ⁽ p , q ) “^- A s ⁽ p , q )-                              ⁽⁶⁹⁾

Другими словами, в рассматриваемом случае интеграл A_s ( p , q ) набирается на первой осцилляции, в то время как интеграл A_c ( p , q ) набирается на второй осцилляции.

7. Случай больших значений аргументов p “ q » 1

В случае, когда параметры p и q велики и соизмеримы, метод перевала может внести в расчеты заметную погрешность, поскольку при p « q стационарная точка расположена достаточно к нижнему пределу интегрирования. Для того чтобы построить искомый алгоритм, представим интеграл A_s ( p , q ) в виде:

1 ^p dx

A_s ( p , q ) = ^— f—sin( x )cos( q^x / p ) -           (70)

² 0 ^x

Разложим в ряд Тейлора косинус, стоящий под знаком интеграла

.    1 p dx . . .      ( - 1) n I q ² x

A s ⁽ p , q ) = т I — siⁿ⁽ x ) L 7TT7 1 — 2 0 x        n =0 (2 n )! l p

n

.

В результате мы приходим к очевидному соотношению

A c ⁽ p , q ) =

A s ⁽ p , q ) = 2Sⁱ⁽ p ) ^-

”

= 1 :

² n =0

/ . x n +1,2 ( - 1) ⁿ I qL I (2 n + 1)! ( p J

j x^{n - 1,2}cos( x ) dx .

-

1 ^ ² n =0

( - 1) ) (2 n + 2)!

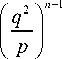
p j xn sin xdx.

Интеграл в формуле (77) удобно выразить через неполную гамма-функцию:

Интеграл, фигурирующий в формуле (72), вычисляется элементарно. В итоге мы приходим к следующему выражению

j x n ^{- 1,2}cos( x ) dx =

= Re i n ^{+ 1/2} y ( n + 1/2, - ip ).

A s ⁽ p , q ) = 2Sⁱ⁽ p ) ⁺

Тогда

/ _o X n + 1         / \

1 ”   / n ⁿ ( л ² 1     n (ИХ

+ 'v ¹ ''    I q -I   Y k | | n I

2 ^: (2 n + 2)! ( p J ² I k J

A c ⁽ p , q ) = -Z ² n =0

/ . x n +1,2

( - ¹) ⁿ | qL I     _x

(2 n + 1)! ^ p J

x Re |^ i n ^{+ 1/2} у ( n + 1/2, - ip ) J .

x[ p^{n k} cos ( p + k n /2 ) -5 _knn !cos ( n n / 2 ) ^| .

В результате достаточно громоздких, но несложных преобразований мы приходим к следующему выражению для A_s ( p , q ):

Воспользуемся тем, что

Y ( n + 1/2, - ip ) =

= Г ( n + 1/2) -Г ( n + 1/2, - ip ),

As (p, q) = 2si( p)+ cos p (-1)nn! I q21n+1

+ c n( p ) -

2 ^: (2 n + 2)! ( p J   [ ⁿ '^

n + 1

sin p v ( - 1) n ! Г q ¹          , .

2 S^ n + 2)! [ p ^J s ^{[( n} - ^1)/2]( p

- 1 "  ( - 1) ⁿ (2 n )! I q 1 ² n ^{+ 1}

2 ² (4 n + 2)! ( p J ’

а также тем, что для неполной гамма-функции имеет место асимптотическое разложение:

Г ( n + 1/2, - ip ) «

« ( - ip ) ^{n 1/2} exp( ip )

1 + i

n - 1/2

+ ...

где [ a ] - целая часть числа a , a s_n ( z ) ( c_n ( z )) — частичная сумма ряда Тейлора для синуса (косинуса). Полученное выражение весьма похоже на соотношение (26). Однако, в отличие от формулы (26), оно содержит только функции вещественного аргумента.

Перейдем к рассмотрению интеграла A_c ( p , q ). Проделаем выкладки, полностью аналогичные, тем, что были выполнены для интеграла A s ( p, q ). Для этого преобразуем выражение (2) к виду

A c ( p , q ) = 1J dx cos( x )sin( q^x / p ). ² 0 ^x

Разложим подынтегральное выражение в ряд Тейлора. В результате получаем:

A c ⁽ p , q ) =

= 1 j dx cos( x ) Ё ² 0 ^x         n =0

( - 1) ⁿ

(2 n + 1)!

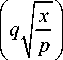
2 n +1

Поскольку под интегралом стоят аналитические функции, операции суммирования и интегрирования коммутируют. Следовательно

p

Следовательно, для случая p » 1 получаем

A c ⁽ p , q ) »- Z ² n =0

( - 1) ⁿ (2 n + 1)!

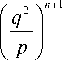
■ Re

i—(n+1/2)                                  1 л • i- -i e 2      Г(n +1/2) - ip"-1/2e,p [1 +...]

откуда получается выражение, удобное для проведения численных расчетов

sin p sin q

A c ⁽ p , q )»—т—-+

2 p

+ 1     ( - 1) ⁿ Г ( n + 1/2) | q^ I

2V2 n :0    (2 n + 1)!     ( p J

x

Заключение

Резюмируем вышесказанное следующим образом.

Поскольку численные значения величин A_s ( p , q ) и A_c ( p , q ) вне задачи нахождения функции отклика оптикоэлектронного датчика не имеют самостоятельной ценности, постольку в работе исследовалась только скорость сходимости и точность различных методов расчета указанных интегралов.

• 1.    В работе построены простые аналитические выражения для расчета интегралов специального вида.

• 2.    Проведен численный анализ полученных аналитических выражений.

• 3.    Показано, что использование идеологии метода перевала позволяет существенно повысить вычислительную эффективность алгоритмов, необходимых для обработки сигналов, поступающих с оптикоэлектронной датчиковой аппаратуры.

• 4.    Показано, что нелинейная оптическая функция отклика, исследованная в работах [1,2], может быть рассчитана в реальном времени на основе гибридного алгоритма, сочетающего в себе все перечисленные в данной работе подходы, каждый из которых оптимален в определенной области значений аргументов p и q .

Представляется перспективным использование разработанного набора алгоритмов для решения задачи синтеза оптикоэлектронных датчиков перемещений с контролируемой нелинейностью оптической функции отклика.

Приложение

Определения и обозначения, используемые в работе

В настоящей работе используются следующие стандартные определения, обозначения и соотношения, подробно описанные в справочниках [4, 5]:

Hn (x) = dn         ج полином Эрмита

= ( - 1) n exp⁽ x ²)—exp( - x ²⁾

dxn

1 dⁿ

P ( z ) =-- ( z ² - 1) - полином Лежандра

2n n!dzn да

Г ( z ) = j exp( - t ) t^{z - 1} dt - гамма-функция 0

Г ( z + n )

( z ) =--символ Похгаммера

Г ( z )

z

Y ( a , z ) = j exp( - t ) t^{a - 1} dt – неполная гамма-функция 0

erf( z ) =     j exp( - t ²) dt - интеграл вероятностей

V n g

—inerfc(z) = -in 1erfc(z) - кратный интеграл веро-dz ятностей, причем по определению i ^rfc(z) = -=exp(-z2), V n

z

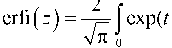
мнимого аргумента .

интеграл вероятностей

y

F ( y ) = exp( - y ²) j exp( t ²) dt - интеграл Досона.

z

x Г I П 2 It

C ( z ) = j cos I —t I dt o V ^{2 J}

– интеграл Френеля.

z

I П I

5 ( z ) = j sin I — t I dt - интеграл Френеля.

0 ^{V 2 J}

/ x v+2 к

z I

Uv (z, ^) = E (-1) I?I   Jv+2 k © - фУнКЦия Лом- k=0       V^J меля двух аргументов.

n (z)k en(z) = / ,--частичная сумма ряда Тейлора для к=0 k !

экспоненты (lim e_n ( x ) = exp( x )). n ^да

/ X         ^(-1) k 2 к +1               „ „     „ „ „

Sn (x) = / .-------x - частичная сумма ряда Тей- k:^(2 к+1)!

лора для синуса (lim s_n ( x ) = sin x ). n ^да

/ X V ^{( - 1) k} 2k             „ „     „ „ „

Cn(x) = / .----x - частичная сумма ряда Тейлора к-0Л2 к)!

для косинуса (lim c_n ( x ) = cos x ). n ^да