Быстрый итерационный расчет фазовых формирователей мод Гаусса-Лагерра

Моды лазерного излучения - пучки, комплексное распределение в сечении которых описывается собственными функциями оператора распространения света в среде [1]. Фундаментальными свойствами мод являются свойства сохранения своей структуры и ортогональности при распространении в среде [1]. В [1] было показано, что использование фундаментальных свойств мод лазерного излучения позволяет увеличивать число каналов в оптоволоконных системах связи и системах связи в свободном пространстве, создавать высокочувствительные оптоволоконные датчики. Таким образом, разработка элементов, позволяющих формировать и селектировать моды лазерного излучения, является важной задачей совершенствования элементной базы для построения высокоэффективных оптоэлек- тронных систем. В [1] рассмотрен расчет и изготовление фазовых дифракционных оптических элементов (ДОЭ), формирующих заданное модовое распределение (моданов).

В [1] для перехода от комплексной функции пропускания модана к чисто фазовой предложено использовать дифракционное кодирование, основанное на внесении модулированной несущей в фазу элемента (обобщенный метод Кирка-Джонса). Применение такого подхода приводит к низкой энергетической эффективности элементов, что связано с появлением нерабочих дифракционных порядков.

В данной работе рассматривается итерационный подход к расчету фазовых моданов. В работе [2] описан итерационный алгоритм, позволяющий рассчитывать моданы, формирующие группу из че- тырех и более мод, с энергетической эффективностью свыше 90%. Однако во многих случаях стоит задача формирования одномодового распределения из освещающего пучка в заданной области плоскости наблюдения с высокой энергетической эффективностью [1].

Для решения этой задачи в [3] был предложен итерационный алгоритм расчета ДОЭ, формирующего моду Гаусса-Эрмита (1,0) в полезной области фокальной плоскости из Гауссова пучка.

Элемент, рассчитанный процедурой [3], был впоследствии изготовлен методом равномерного травления полиметилметакрилата, нанесенного на подложку из кварцевого стекла, по 16 уровням [4]. Изготовленный элемент был рассчитан как добавка к линзе и предназначен для работы с пучком гелионеонового лазера HNA-180. На Рис.1 представлено двумерное распределение интенсивности, замеренное CCD-камерой в ходе натурного эксперимента по исследованию изготовленного модана [4]. Измерение производилось в выходной плоскости фурье-каскада, на вход которого подавалось одномодовое распределение, сформированное рассчитанным элементом. Таким образом, результаты натурного эксперимента [4] подтверждают целесообразность применения итерационной процедуры [3] к расчету однопучковых моданов.

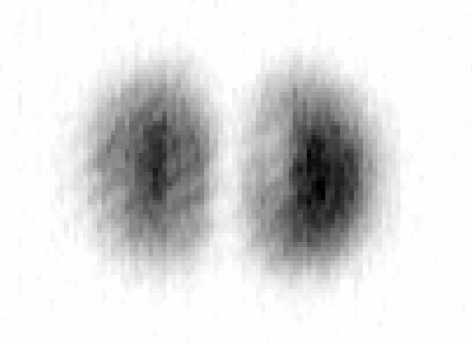
Рис. 1. Распределение интенсивности, сформированное элементом, согласованным с модой Гаусса-

Эрмита (1,0).

Однако, основным недостатком процедуры [3] является необходимость больших вычислительных затрат, связанных с вычислением двух двумерных преобразований Фурье на итерацию. Это ограничение является существенным так как, во-первых, для изготовления реального элемента требуется полутоновая маска с размерами, как минимум 2048*2048 отсчетов, во-вторых, как показывает практика, подбор оптимальных параметров требует неоднократного итерационного расчета и моделирования ДОЭ.

В работе [5] показано, что в случае, если заданное распределение обладает радиальной симметрией, двумерное преобразование Фурье сводится к преобразованию Ганкеля, которое может быть вычислено с помощью трех одномерных преобразований Фурье. Радиальной симметрией обладают, например, моды Гаусса-Лагерра с нулевым значением второго порядкового номера [1], моды Бесселя.

Для формирования обобщенных мод Гаусса-Лагерра произвольных порядков можно использовать преобразование Ганкеля того же порядка, что и второй порядковый номер моды [5].

Данная работа посвящена расчету и исследованию элементов, формирующих обобщенные моды Гаусса-Лагерра из Гауссова пучка, и исследованию свойств сформированного одномодового пучка средствами вычислительного эксперимента.

Для расчета предлагается модификация алгоритма [3] для радиально-симметричного случая. На примере расчета моданов, формирующих обобщенные моды Гаусса-Лагерра показано, что развиваемый подход позволяет формировать заданное распределение с энергетической эффективностью, значительно большей, чем у элементов, рассчитанных методом Кирка-Джонса [1].

• 1.    Постановка задачи формиирования одномодового распределения.

• 2.    Построение процедуры расчета формирователей обобщенных мод Гаусса-Лагерра

Рассмотрим постановку задачи расчета фазового однопучкового модана. Пусть элемент с функцией комплексного пропускания W₁(u, v) , определенной на апертуре D , освещается пучком света с распределением комплексной амплитуды в сечении W₀ (u, v) . Комплексное распределение в плоскости непосредственно за элементом имеет вид W ( u,v ) = W 1 (u, v)W₀(u,v). В случае выполнения условия параксиального приближения и условия дальней зоны, преобразование Френеля-Кирхгофа, описывающее связь комплексного распределения за элементом W(u,v) с распределением в плоскости наблюдения w(x,y) , сводится к преобразованию Фурье [6]:

При соблюдении упомянутых условий можно сформулировать задачу синтеза фазового ДОЭ, формирующего заданное комплексное одномодовое распределение w (x,y) в области M плоскости наблюдения, как задачу поиска такой функции w(x,y), которая           удовлетворяя           условию

JJ|w(x,y) - ^(x,y)|2dxdy = 0, имела бы амплитуду M фурье-спектра C^Io(u,v) , где Io (u,v) = |Wo(u,v)|2-распределение интенсивности освещающего пучка, C - константа, выбираемая из условия сохранения энергии.

В [3] рассмотрен подход к построению итерационной процедуры расчета однопучкового мода-на. Для появления свободных параметров, необходимых для работы итерационной процедуры, в плоскости наблюдения выделяется “полезная” область M , содержащая формируемое изображение y (x>y) , и некоторая “вспомогательная” область.

На каждой итерации в фокальной плоскости осуществляется замена имеющегося распределения в “полезной” области на требуемое одномодовое распределение и обнуление точек фокальной плоскости, лежащих вне “полезной” и “вспомогательной” областей. Значения комплексной амплитуды в точках “вспомогательной” области являются свободными параметрами. Затем пересчитывается распределение в плоскости ДОЭ, где осуществляется подстановка амплитудного распределения осве щающего пучка W0 (u, v) . После этого опять вы- полняется переход в фокальную область элемента.

В качестве начального приближения в [3] выбиралось распределение, содержащее в “полезной” области заданное одномодовое распределение v(x, y) и случайное предыскажение во “вспомога- тельной”. Доля энергии освещающего пучка, приходящаяся на точки “вспомогательной” области является “платой” за приведение амплитуды Фурье-образа формируемого изображения |Wn(u,v)| = |f-1 (wn (x,y)) к форме освещающего пучка W0 (u, v) .

Разработанная процедура является, по сути, модификацией известной процедуры Фьенапа [7] со специфическим ограничением, накладываемым на распределение в плоскости наблюдения. В [8] показано, что в случае, если формируемое изображение w ( x,y ) = w(r) и освещающий пучок

I(u,v) = I(p),r = ^x^ + y2 , p = Vu2 + v2 обладают радиальной симметрией, преобразование (1) может быть сведено к преобразованию Ганкеля 0-го порядка:

w(r) =H0(W (p)) \w (p) = H0 (w (r))

В этом случае постановка задачи расчета ДОЭ выглядит следующим образом: необходимо найти функцию w(r), которая удовлетворяя условию j Wr) - ^(r) |2 rdr = 0 , имела бы амплитуду Фу-r < R i рье-спектра еУыР). где Io (P) = Wo(p)|2, R1- радиус полезной области (например, радиус сердцевины градиентного оптического волновода) (Рис 2). В работе [5] показано, что вычисление преобразования Ганкеля (2) легко сводится к вычислению трех одномерных преобразований Фурье. Таким образом, в предположении, что “вспомогательная” область также обладает радиальной симметрией, итерационная процедура [3] существенно упрощается и требует вычисления лишь шести одномерных преобразований Фурье на итерацию.

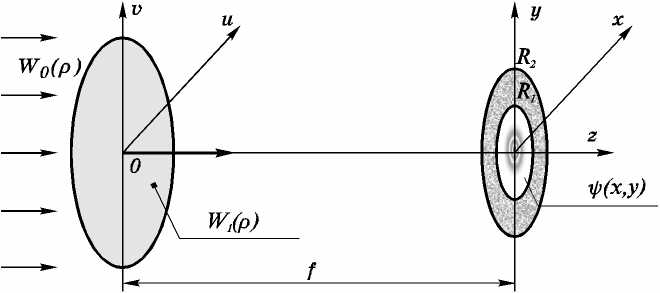
Рис. 2. Постановка задачи расчета ДОЭ, формирующего радиально-симметричную моду.

Интересно отметить, что, обладая эффективной процедурой расчета радиально-симметричных моданов, можно получить распределение, описываемое любой обобщенной модой Гаусса-Лагерра, формируя нерадиально-симметричную фазовую “добавку” соответствующим фазовым фильтром, выбираемым из следующих соображений. Для формирования в дальней зоне Фраунгофера обобщенной моды Гаусса-Лагерра [1]:

vL ^{( r} , ^ =

2 ^n(n - m ) ГО ( n !) 3

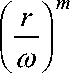
m Ln

x exp

2 ro¹

( r ² )     /

= ~ nm ⁽ r ^)ex P ⁽± im ^ )                           ⁽³⁾

(где го - фундаментальный радиус моды, 9 - угол в полярных координатах, L -полином Лагранжа, n,m -порядковые номера мод) необходимо на входе иметь следующее распределение комплексной амплитуды:

2п -

0 0

0             L 0

Используя справочный интеграл [8]:

i m 2 n

J_m(x) = — fexp ( ± i mt ) exp [ - i xcos(t) ] dt    (5)

^{2 n} 0

легко свести (4) к следующему виду:

Т ( р , v ) = exp ( ± i m v ) 2 m x

X J V .. (r)J_m (r p )rdr = ~( p ) exp ( ± i m v )

JJ w n ^{( x} , У )|² dxdy e n = м ----------,

JJ 1 ₀( u , v ) dudv

D

Таким образом, для формирования функции (3) нам нужно рассчитать только радиальный множитель искомой функции:

где w_n ( x , y ) - комплексная амплитуда сформированного распределения на n -ой итерации, и удельная мощность эталонной моды в полезной области [1].

A to

~      2 П

^ ⁽ P ) = Im J V nm^(r)Jm^(r P ^)rd r ,               ⁽⁷⁾

i ₀

Zn =

C о JJ w_n ( x , У ) V ( x , У ) dxdy 2 ,

M

который представляет собой преобразование Ганке-ля m -го порядка.

3. Экспериментальные результаты.

В данной работе производился итерационный расчет ДОЭ, формирующего из Гауссова пучка с распределением интенсивности

Константа C 0 выбирается из условия орто-

гональности базиса модовых

JJ v ( x , У "V * ( x , У ) dxdy = 1:

«

функций,

I 0⁽ P ) = ^ex P

эталонное распределение, описываемое модой лазерного излучения y (r), внутри области M с радиусом R 1 . В качестве эталонных распределений выбирались обобщенные моды Гаусса-Лагерра (1,0), (4,0), (2,2).

В качестве начального приближения выбиралась функция

C 0 =          ¹ 2   =.              (12)

JJ w n ^{( x} , У ) ^dxdУ

M

Для строгой оценки доли энергии освещающего пучка, идущей на формирование эталонной моды в полезной области M фокальной плоскости вычислялось значение приведенной энергетической эффективности

En = en Z n

[ V ^(r) w o (r)   '// / (И

I ⁰

r <  R 1

R 1 < r < R₂ . r >  R₂

Предлагаемая процедура естественным образом обобщается на случай расчета ДОЭ для формирования любого комплексного распределения вида w ( r )exp( imP) , m=0,1,2..., если входной пучок

В качестве %( r) выбиралась случайная вещественнозначная функция, равномерно распреде-

ленная на отрезке

, параметр ц оп-

обладает радиальной симметрией. Однако соотношение энергетической эффективности и точности формирования заданного распределения будет определяться конкретной спецификой задачи. Отметим также, что в случае, если формируемое изобра-

ределяет соотношение долей энергии, приходящихся на “полезную” и “вспомогательную” области начального приближения. R 2 - внешний радиус вспомогательной области. Введение случайного предыскажения во “вспомогательную" область приводит к появлению свободных параметров, необходимых для работы процедуры. Для пересчета поля из плоскости элемента в фокальную плоскость и обратно использовалось процедура быстрого вычисления преобразования Ганкеля [5].

Элементы рассчитывались как добавка к линзе со следующими значениями физических параметров: фокусное расстояние f=50 мм, длина волны X =0.6328 мкм , радиус апертуры ДОЭ R_ap=10 мм , фундаментальный радиус формируемой моды w=5.6 мкм , радиус освещающего Гауссова пучка о=3-3.5 мм , количество итераций N=10 .

В качестве критериев качества формирования заданного распределения были определены энергетическая эффективность

жение содержит только нулевые значения в точках вблизи оптической оси, пересчет поля с апертуры в фокальную плоскость и обратно может осуществляться, используя вычисление всего лишь двух одномерных преобразований Фурье на итерацию [9]. Примером такого распределения являются обобщенные моды Гаусса-Лагерра с равными значениями порядковых номеров (Рис. 5).

В работе [1] было показано, что Гауссовы моды не только являются собственными функциями

оператора распространения света в градиентных оп-

тических волноводах, но также сохраняют свою структуру и ортогональность при распространении в

пространстве.

В [10] было показано, что Гауссовы моды не меняют своей структуры и при прохождении Фурье-каскада. В этом случае меняется лишь значение фундаментального радиуса моды ю на to F , определяемое параметрами Фурье-каскада:

X f

Распределения фазы и амплитуды, полученные в результате расчета и моделирования моданов, а также в результате моделирования распространения сформированных одномодовых пучков, приведены на Рис. 3-5.

1                 2                3

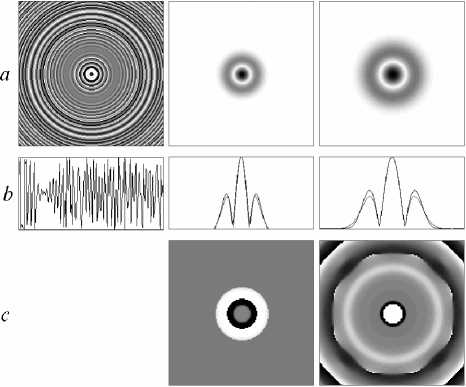
Рис. 3. Формирование моды Гаусса-Лагерра (1,0): распределение фазы ДОЭ (1а), ее радиальное сечение (1b), сформированное амплитудное распределение в полезной области (2а), его радиальное сечение (штриховой линией показано сечение эталонной моды) (2b), сформированное фазовое распределение в полезной области (2c) (диапазон значений [-K,nj), в третьем столбце приведены результаты моделирования прохождения сформированной моды через Фурье-каскад.

1                 2                3

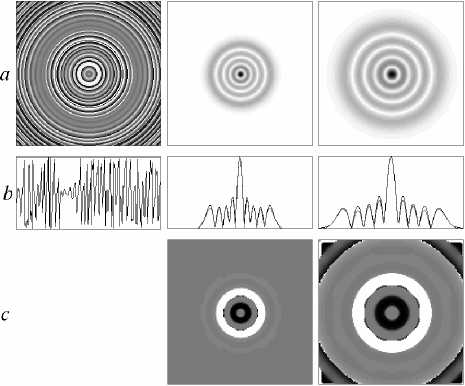
Рис. 4. Формирование моды Гаусса-Лагерра (4,0): распределение фазы ДОЭ (1а), ее радиальное сечение (1b), сформированное амплитудное распределение в полезной области (2а), его радиальное сечение (штриховой линией показано сечение эталонной моды) (2b), сформированное фазовое распределение в полезной области (2c) (диапазон значений [-л,л]), в третьем столбце приведены результаты моделирования прохождения сформированной моды через Фурье-каскад.

Интересно отметить “вращение” моды (2,2) при прохождении Фурье-каскада, что объясняется наличием винтовой фазовой добавки (Рис. 5).

Кроме того, в данной работе проводилось сравнение элементов, рассчитанных предложенной процедуры, с элементами, рассчитанными методом Кирка-Джонса для того же набора физических параметров. Значение оценки e k энергетической эффективности элементов, рассчитанных методом Кирка-Джонса, находилось по методике, приведенной в [1]. Для выбранного набора параметров значение e k не превышало 14.5%.

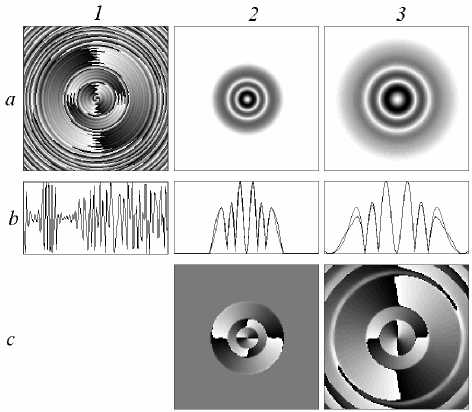
Рис. 5. Формирование моды Гаусса-Лагерра (2,2): распределение фазы ДОЭ (1а), ее радиальное сечение (1b), сформированное амплитудное распределение в полезной области (2а), его радиальное сечение (штриховой линией показано сечение эталонной моды) (2b), сформированное фазовое распределение в полезной области (2c) (диапазон значений [- л,л]), в третьем столбце приведеныре-зультаты моделирования прохождения сформированной моды через Фурье-каскад.

Результаты вычислительного эксперимента (Таб. 1) показали, что предложенная итерационная процедура позволяет рассчитывать моданы, формирующие обобщенные моды Гаусса-Лагерра с энергетической эффективностью в 2-3 раза большей, чем моданы, рассчитанные с помощью метода [1]. При этом содержание заданной моды в формируемом пучке составило свыше 95%..

Таблица 1.

Номера моды	о , mm	e, %	С,%	E ,%
(1,0)	3	40.1	97.5	39.0
(2,0)	3.3	35.4	96.4	34.1
(2,2)	3.5	62.8	96.7	60.6
(4,0)	3.5	33.7	96.4	32.4

Заключение

В данной работе рассмотрен высокоэффективный итерационный метод расчета формирователей мод Гаусса-Лагерра. Результаты вычислительных экспериментов демонстрируют весьма ощутимый выигрыш в энергетической эффективности по сравнению с методом Кирка-Джонса.

В то же время, применение эффективной процедуры расчета, использующий вычисление всего шести одномерных преобразований Фурье на итерацию, позволяет рассчитывать моданы с реальным числом отсчетов, не прибегая к использованию высокопроизводительных вычислительных систем. Используя предлагаемый подход, нетрудно рассчитать элемент, формирующий любую обобщенную моду Гаусса-Лагерра с числом отсчетом 10000*10000 и более, на обычном персональном компьютере.

Результаты моделирования прохождения сформированной моды через Фурье-каскад подтверждает высокое качество формирования ква-зиодномодового пучка. Результаты натурных испытаний моданов Гаусса-Эрмита [4], рассчитанных процедурой [3] дают основание полагать, что элементы, рассчитанные с помощью предлагаемой в данной статье процедурой, могут быть успешно реализованы, например, методом многоуровневого литографического травления резиста, нанесенного на подложку из кварцевого стекла. Кроме того, может быть использована технология [11] синтеза радиально-симметричных ДОЭ. В заключение отметим, что развитие методов расчета элементов, формирующих заданное модовое распределение, позволяет эффективно решать не только задачи, связанные с уплотнением каналов связи в оптических телекоммуникационных системах. Элементы формирующие радиально-симметричные моды, рассмотренные в данной статье, могут найти применение для создания высокочувствительных аку-стооптических преобразователей, основанных на использовании свойств распространения мод в волокне с параболическим профилем показателя преломления [1].

В [1] на результатах натурного эксперимента показано, что оптоволоконные датчики, основанные на селективном возбуждении мод Гаусса-Лагерра (1,0) или (2,0) в волокне, в 4-8 раз чувствительнее, чем у традиционных оптоволоконных датчиков, основанных на измерении полной энергии света, прошедшего через деформированное оптоволокно.