Быстрый поиск опорных фрагментов при фрактальном кодировании изображений

В работе предлагается метод быстрый метод нахождения соответствующих фрагментов изображения в задаче фрактального кодирования на основе приближения многочленами второго порядка. Дается описание двухэтапного рекуррентного алгоритма, приводятся оценки вычислительной сложности.

Постановка задачи, общая схема фрактального кодирования

Фрактальное кодирование изображений является одним из наиболее перспективных на сегодняшний день методов компрессии изображений с потерями [1,3], отличается высокой степенью сжатия и высокой скоростью восстановления изображения. Классическая схема фрактального кодирования предполагает разбиение изображения I на прямоугольные непересекающиеся области, называемые доменами :

a

D = {D,.. Da},   J D= I,   ДП Dj= 0, i * j, i =1

Задача минимизация ошибки (1) по коэффициентам яркостного преобразования R * = argmin E ( D,Ri\ я

эквивалентна максимизации значения коэффициента корреляции:

R * = arg max г ( D , R i ) , я ¹

где

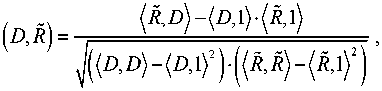
и поиск сжимающего аффинного преобразования области изображения, наилучшим образом аппроксимирующего данный домен. Для поиска аффинных преобразований на изображении выделяются ранговые области - прямоугольные области Я = { R , .. R b } размера, превышающего размеры доменов. Рассматривается линейная аппроксимация D домена D ранговой областью R :

d (n,, n 2) = к ■ г (n,, n 2) + e,

( n , , n 2 ) е W = [ - N , N ][ - M , M ] ,

E ( D , R ) = min| D - D ||2 =                        ⁽¹⁾

= min Z (d (n,, n 2)-к ■ г (n,, n 2)-e )2, к' e (n,, n 2 )eW где N, M - размеры домена, г - ранговая область, уменьшенная до размеров домена, E - ошибка аппроксимации.

Совокупность преобразований для всех доменов вместе с параметрами соответствующих ранговых областей образует аффинный коллаж изображения, на основе которого на этапе восстановления можно с помощью простого и быстро сходящегося итерационного процесса получить аппроксимацию исходного изображения. Сжатие основано на том, что параметры аффинных преобразований занимают в памяти ЭВМ гораздо меньше места, чем пиксели исходного изображения.

Легко показать [6, 8], что оптимальные коэффициенты яркостного преобразования и соответствующая ошибка аппроксимации вычисляются на основе средних значений и дисперсий доменной и масштабированной ранговой области, а также их взаимной ковариации.

(^{D ,]} = Z ^d ( n i , n 2 ) , ( ^{R ,1}) = Z ^f ( n i , n 2 )

( n_b n 2 ) e W                                 ( n_b n 2 ) e W

(D , R ; = Z d ( n , , n 2 ) г ( n , , n 2 ) , ( n , , n 2 ) e W

(D , D) = Z d ² ( n i , ⁿ 2 ) , RR , R = Z ^? ( n i , ⁿ 2 ) . ( n , , n 2 ) e W                                        ( n , , n 2 ) e W

При этом

a =

b =

(2 N + 1) ■ (2 M + 1) ■ (D , R ^ - ^ R , 1) ( D , 1)

R , R ^ - <^ R ,1)

(2 N + 1) ■ (2 M + 1)

■ ( D ,] - a ■ ( R ,1).

В настоящей работе рассматривается поиск на множестве ранговых областей размера в К раз большего размеров домена. Указанное множество образуется всевозможными сдвигами ( n , , n ₂) по полю изображения и поворотами на произвольный угол ф (ортогональное подмножество аффинных преобразований координат с заданным масштабным коэффициентом).

Общая схема нахождения соответствия между фрагментами

Основным недостатком фрактального сжатия является большая вычислительная сложность этапа кодирования изображения, вызванная необходимостью полного перебора всех возможных ранговых

областей и вычисления их взаимных ковариаций с доменными областями.

Можно выделить две основные группы способов, используемых для повышения скорости фрактального кодирования.

Методы первой группы основаны на замене вычисления ошибки аппроксимации (1) вычислением более простого функционала [4, 6, 8]. Из методов этой группы выделяются методы сравнения значений рекурсивно вычисляемого набора инвариантных к повороту признаков (моментных инвариантов и др.) [4]. При этом остается открытым вопрос соответствия значения выбранного функционала и ошибки (1). Другая подгруппа методов, чаще всего использующих энтропийные признаки [4, 5], осно- вана на отсечении заведомо непригодных ранговых областей, имеющих сильно различные статистические характеристики с доменной областью.

Вторая группа методов основана на ограничении набора рассматриваемых ранговых областей (например, повороты только на углы, кратные 90 ° , или сдвиги с «прыжком» через экспериментально подбираемое количество отсчетов) [7, 8]. Дополнительно эти методы часто снабжаются ускоренными процедурами вычисления ковариации на основе дискретных ортогональных преобразований [8].

В настоящей работе рассматривается двухэтапный метод поиска ранговых областей (рис. 1). На первом этапе производится поиск потенциально пригодных ранговых областей. Ранговая и доменная область аппроксимируется многочленами второго порядка, коэффициенты которых вычисляются рекурсивно. Затем производится простая процедура нормализации коэффициентов к повороту и вычисление взаимной корреляции многочленов (при этом попутно отбраковываются области с сильно различными статистическими характеристиками). Потенциально пригодные фрагменты (вместе со значениями угла поворота) получаются после обработки поля ошибки пиковым фильтром [9], оставляющего только локальные максимумы корреляции выше за-

На втором этапе значения возможных положений ранговых областей уточняются методом покоординатного спуска, с использованием найденных на первом этапе начальных приближений координат центра и угла поворота. Из множества найденных областей выбирается область с наилучшей аппроксимацией.

Достоинствами метода являются малая теоретическая сложность вычисления за счет рекурсивного вычисления признаков, наличие теоретических оценок, связывающих ошибку (1) с выбранными на первом этапе функционалами, рассмотрение поворотов доменных областей на произвольный угол, а также наличие второго этапа уточнения положения ранговой области.

Рекурсивная локальная аппроксимация фрагментов изображений поверхностью второго порядка

Решим вопрос о нахождении коэффициентов аппроксимации изображения x ( n ₁, n ₂) в скользящем окне поверхностью второго порядка:

Г                              12

е ² = ^     ^ a ij n 1 n 22 - x ( n 1 ,n 2 )    ^ min, (5)

(n1,n2)eW _0

Описываемый ниже метод вычисления коэффициентов поверхностей и нормализации их к повороту применим для поверхностей произвольного порядка, однако при использовании больших порядков увеличивается сложность вычисления взаимной ковариации поверхностей (см. ниже), поэтому в работе предложено остановиться на данного порога.

поверхностях второго порядка.

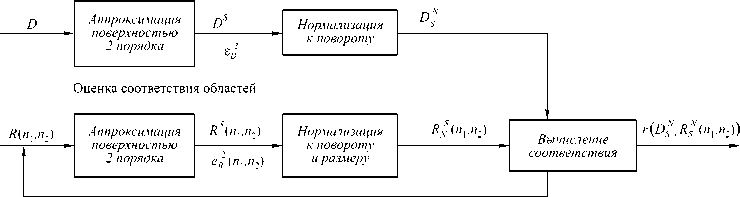
Выделение потенциально пригодных областей

Нахождение наилучшей ранговой области

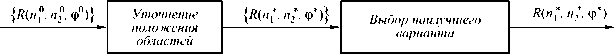
Рис. 1. Общая схема нахождения ранговой области, наилучшим образом аппроксимирующей доменную

Частные производные в (5) по коэффициентам полинома, после несложных преобразований можно записать в виде:

I a.

i + j <2

I   n ⁺ i n 2 ⁺ j

_ ( n i , n 2 ) ^e W

= ц_г,. ,0 <  i ' + j ' <  2,

имущественного направления. Матрица пересчета старых координат через новые записывается в следующем виде:

J ni = An - Bn2,

In 2 = Bn + An 2,

n _i = Cos ф n_i - Sin ф n 2 ,   (Ю)

n ₂ = Sin ф n_i + Cos ф n ₂.

где ц_гг - начальные моменты порядка (i’,j’)

ц . _j ( n_i,n ₂) =    I   m i m^x ( n_i - m_i,n ₂ - m ₂ ) . (7)

( m i , m 2 )e W

При этом ошибка аппроксимации:

^{e 2} = I x ⁽ n i , n 2 ^{) 2} - I a j Ц .

( " i , n 2 )e W                      i + j <2

Заметим, что можно заранее вычислить как элементы матрицы

N = 1 I пГ'п'

I ( " i , n 2 )e D

, i ' + j ' <  2, i + j <  2

так и элементы обратной матрицы N-1. Поэтому, если мы предварительно вычислили моменты Цу г, то для вычисления на их основе коэффициентов aij по (6) необходимо дополнительно выполнить 62 = 36 умножений и сложений, а для вычисления ошибки e2 еще 6 умножений и сложений. Начальные моменты и значение I x(ni, n2)2 (необхо-("i ,n2 )еW димое для вычисления погрешности) формируются рекурсивно [2, 9]. Для их вычисления также требуется по 62 = 36 операций сложения и умножения.

Нормализация поверхности второго порядка относительно поворота и размера

Пусть найдены из (6) поверхность второго порядка, аппроксимирующая изображение в окне:

y ⁽ n i , ⁿ 2 ) = a 20 n i² + a ll n iⁿ 2 +

2                             .                              (8)

⁺ a 02 n 2 + a io ⁿ i + a oi ⁿ 2 ⁺ a 00

Подставив (10) в (8), получаем выражения для расчета нормализованных (преобразованных) коэффициентов поверхности (8) в новой системе координат ( n ₁ ^' , n ₂ ^' ):

a '20 = A2 a 20 + ABaii + B2 a 02, a'ii =-2ABa20 + (A2 -B2)aii + 2ABa02, a'02 = B2a20 - ABaii + A2a02, a 'i0 = Aai0 + Ba 0i, a 0i = Aa0i - Bai0, a 00 = a 00 .

Из (10), используя формулу для тангенса двойного угла, можно выразить A = Cosф и B = Sinф через C = tg2.ф без необходимости вычисления прямых и обратных тригонометрических функций:

<

"V 2" 24! + ё ’

B = "  I ^ + / ⁱ . \² 27i + c 2

При нахождении конкретных значений А и В возникает задача выбора знаков " перед радикалами. Эта неоднозначность связана с тем, что при повороте изображения на угол 2п имеется четыре по ложения угла ф, отличающихся на у, при которых ц1(Ф) = 0 (8). Снятие неоднозначности (выбор определенного значения угла поворота) осуществляется на основе анализа знаков коэффициентов a10, a01

и сравнения значений | a ₂₀ |и | a ₀₂ |

Общий алгоритм расчета нормализованных к углу поворота коэффициентов поверхности (8) состо-

Пусть [9] стандартное (нормализованное к повороту) положение изображения определяется соотношением ц ₁₁ = 0. При этом значение угла ф , на которое надо повернуть исходное изображение для нормализации, рассчитывается в виде:

C = tg 2 ф = -З Ц ¹^,

^Ц 20 ^Ц 02

ит из следующих шагов:

Вычисляется C =

2 Ц 11

^Ц 20   ^Ц 02

Рассчитываются <

= ^2+ 27Г+С2, b = 11 - /1 .

N ² 2^1 + c¹

.

ф = ^arctan—2 ^ — + t ^П , t = 0,i,2,3,      (9)

• ^{2        Ц} 20 - ^Ц 02     ²

где ц - начальные моменты (7).

Пусть ( n ₁ ^' , n ₂ ^' ) – новая ортогональная система координат, в которой ось n ₁ ^' направлена вдоль пре-

• 3)    В соответствии с (11) вычисляются преобразованные коэффициенты

a '₂₀ , a '₁₁ , a '₀₂ , a '₁₀ , a '₀₁ , a '₀₀ .

• 4)    Если не выполняется условие | ^{a 20} | > | ^{a 02} |, то производится замена ^ф = ^{ф + П} и замена

a 20 = a 02 , a 02 = a 20 , a 11 =- « 11

a 10     a 01 , a 01       a 10 , a 00 a 00 "

• 5)    Если не выполняется условие а₁₀ >  0, а при а ₁₀ = 0 - а ₀₁ >  0, то производится замена

п

Ф = ф + — и замена a 20 = a 20, a 02 = a02, a 11 = a11, a 10 = - a10, a 01 = - a01, a 00 = a00"

Прямой подсчет количества операций, требуемых для нормализации значений признаков с помощью вышеприведенного алгоритма, дает следующие оценки:

Таблица 1

Наименование	Шаг 1	Шаг 2	Шаг 3	Итого
Сложения	1	3	6	10
Умножения (без учета умножений на 2)	1	2	10	14
Извлечение корня		3		3
Итого	3	5	16	23

Легко показать (сделав замену в (8) n , = n 1 / K , n ₂ = n ₂ / K ), что для приведения размеров ранговой области к размеру доменной (уменьшения в К раз) необходимо коэффициенты поверхности преобразовать следующим образом:

a 20 = a 20 / K 2, an = a11 / K 2, a 02 = a 02 / K 2, a10   a10 / K,a 01

a 01 / K , ^a 00    a 00 "

Нахождение оптимальных коэффициентов яркостного преобразования поверхностей

При поиске соответствия областей на изображении самым трудоемким является вычисление взаимной ковариации DD , R^ согласно (3), которое для нормализованных к повороту поверхностей второго порядка имеет вид:

{D N , R N^ = Е ( a 20 n + a 02 n 2 + a_wn + a 01 n 2 + a 00 ) x ( n ] , n 2 )6 D

• ^x ( b 20 n 1² + b 02 n 2² + b 10 ⁿ 1 ⁺ b 01 ⁿ 2 ⁺ b 00 ) "        ⁽¹²⁾

После раскрытия скобок выражение (12) преобразуется к виду (с учетом нулевого значения сумм индексов с нечетными степенями по симметричному окну):

(^DS , ^RS ) = ^a 20 b 20 Е ⁿ 1 ⁺ a 02 ^b 02 Е n 2 ⁺

( n , n 2 ) e W                 ( n , n 2 )e W

• ^{+ (} a 20 ^b 02 ⁺ a 02 b 20 ) Е n 1 n 2 ⁺

( n , n 2 )e W

• ^{+ (} a 20 ^b 00 ⁺ a 00 ^Ь 20 ⁺ a 10 ^b 10 ) Е ⁿ1 ^{+              (13)}

( n , n 2 )e W

• ^{+ (} a 02 ^Ь 00 ⁺ a 00 ^Ь 02 ⁺ a 01 ^b 01 ) Е n 2 ⁺

( n _], n 2 )e W

+a 00 b00(2 N +1)(2 M +1), что требует 19 операций умножения и 10 сложения, если соответствующие суммы степеней индексов вычислить заранее"

Необходимые для вычисления коэффициента корреляции среднее значение и дисперсия доменной области рассчитываются заранее, а среднее значение и дисперсия ранговых областей вычисляются рекурсивно"

После получения корреляционного поля на нем нужно выбрать заданное количество локальных максимумов выше определенного порога с помощью так называемого пикового фильтра [9].

При программной реализации поиск локальных минимумов и их отсечение по порогу или числу, очевидно, можно выполнять с задержкой по вертикали на размер окна пикового фильтра относительно процедуры вычисления ошибок аппроксимации между поверхностями. Это позволяет не создавать промежуточное корреляционное поле, совпадающее размерами с изображением, и снижает требования к расходованию памяти.

Суммарное количество операций сложения и умножения складывается из затрат на вычисление начальных моментов, нахождение коэффициентов поверхности, нормализацию их относительно поворота, вычисление корреляции между поверхностями и составляет не более 200 операций на отсчет.

Имеют место следующие оценки сверху и снизу ошибки аппроксимации доменной и ранговой областей, основанные на неравенстве треугольника:

E ( R , D ) >  E ( D , D s ) - E ( R , R s ) - E ( D s , R s )| ,

E ( R , D ) >  E ( R , R s ) - E ( D , D s ) - E ( D s , R s )|,

E ( R , D ) <  E ( D , D s ) + E ( R_s , D s ) + E ( R , R s )

Оценка сверху позволяет нам сразу получать приемлемые варианты аппроксимации для простых доменных и ранговых областей (хорошо аппроксимируемых поверхностью второго порядка).

Оценки снизу позволяют выбрасывать из списка потенциально пригодных ранговых областей (с малой ошибкой E ( R s , D_s )) сильно отличающиеся по характеристикам (ошибкам аппроксимации поверхностью второго порядка). Использование именно таких «оценок непригодности» представляется более предпочтительным, чем использование энтропийных признаков [5, 6].

Уточнение положения ранговых областей

На втором этапе выполняется уточнение положения ранговых областей из небольшого множества возможных вариантов, каждый из которых характеризуется начальными значениями масштабного коэффициента K ⁰ , центра ранговой области ( n f , n 0 ) и угла поворота ф = ф, - ^ R , равного разности значений угла разворота доменных и ранговых областей относительно стандартного положения.

Методом покоординатного спуска находятся новые значения параметров ранговых областей, соответствующие локальному минимуму ошибки аппроксимации доменной области ранговой:

• ( n * , n * , $ , K * ) = arg min E ( R, D ).

Соответствующие частные производные находятся численно как разности ошибки аппроксимации для двух соседних значений параметров. Данный этап предполагает многократное вычисление взаимной корреляции доменной и ранговых областей. В случае небольшой мощности множества возможных вариантов (на практике, от трех до семи) это не требует больших вычислительных ресурсов.

При реализации метода покоординатного спуска полезно ограничить поле поиска параметров центра окна размерами области для пикового фильтра и масштабного коэффициента, так как при уменьшении масштабного коэффициента может ухудшаться ошибка восстановления даже при уменьшении ошибки аппроксимации [3].

Заключение

В работе предложен двухэтапный метод фрактального кодирования, основанный на приближении изображений поверхностями второго порядка и вычислении соответствия между нормализованными поверхностями. Отличием от известных методов является наличие связи между исходной ошибкой аппроксимации и значением функционала для оценки перспективности ранговых областей, а также рассмотрение ранговых областей, повернутых на произвольные углы. Достоинствами метода также является наличие второго этапа уточнения положения фрагментов и относительно малая вычислительная сложность.

Работа выполнена при поддержке Министерства образования и науки РФ, правительства Самарской области и Американского фонда гражданских исследований и развития (CRDF Project SA-014-02) в рамках российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), а также при поддержке гранта Президента РФ № НШ-1007.2003.01 и грантов РФФИ № 04-01-96507 и № 05-01-96501.