Calculated study of the influence of overheating aluminum melt on the dynamics the granulation process

Цитирование: Скуратов, А.П. Расчетное исследование влияния перегрева алюминиевого расплава на динамику процесса гранулирования / А.П. Скуратов, А.В. Ивлев, А.А. Пьяных // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(1). С. 84-93. DOI: 10.17516/1999-494X-0207

of the crystallization process. In this case, when solving a specific granulation task, the designer or production Manager can give an approximate rapid assessment of the process dynamics, which will significantly reduce labor costs and time.

Mathematical solidification process simulation of a melted drip linked with the analysis of thermal conductivity objectives with consideration of moving borders where the phase transfer occurs. Mathematical models of specified processes represent nonlinear boundary-value thermal conductivity problem with the abruption of the temperature gradient of the phases failure front. All these tasks can be determined as “Stefan’s problems”. The difficulty in the solution of Stefan’s problems lies in the fact that thermal calculations of heating and cooling metal must consider the value of thermophysical characteristics of liquid and solid phases, also their complex heat exchange with the environment. Boundary value problem nonlinear structure connected with the processes of heat-and-mass transfer focused in both equations (internal nonlinearity) and boundary conditions equations (external nonlinearity).

For the first time, the definition of the Stefan problem and its solution were investigated in the classical paper on liquid freezing [2, 3]. When the solution was obtained from a task by authors the principle of self-similarity was implemented, i.e. data of differential equations in partial derivatives to ordinary differential equations were used. The main property of self-similar decisions is that the front of phase changes moves under the law of a square root from time. Later this approach was applied to more complicated tasks by Stefan, domestic and foreign mathematicians. The range of the tasks solved by using this principle is very narrow, but in the theoretical plan, they are of great value as precise solutions to Stephan’s problems.

The most common solution for Stefan’s problems was received by F. Neumann which is considered as standard. The solution is received here for a semi-restricted area which at the initial moment is filled with a liquid phase with the fixed temperature. For the linear heat flux, the solution is found in the form of a tabulated function of mistakes, often appearing in problems of heat conductivity.

In a number of works, the variation method of Biot is used, it based on the introduction of a thermodynamic equivalent of a Lagrange function in mechanics related to a concept of a thermal layer where the profile of temperature is approximated by a power function is applied to the solution of Stefan’s problem. The solving methods which are used: method of serial change of stationary phases; the methods based on representation of the final decision in the form of power series; methods based on the system of ordinary differential equations; reductions by means of a potential theory to integral equations; integral method; method of small parameter; quadrature decisions [4-6]. It should be noted that a big contribution from domestic scientists to development of methods of approximate calculation of hardening of mould pieces was done whose detailed analysis is provided in [2].

Of particular interest is the method developed in recent years “thermal quasi-stationary approximation” to the study of heat transfer processes with relative frame boundaries of phase transformations [7]. This method is based on the construction of asymptotics. Therefore, the nature of the exact composite solution of the problem can be judged by its asymptotic expansion, taking into account some extreme parameters of the process.

For the heat conductivity problems with the relative frame front of phase changes, one of the most efficient methods is the numerical method realized on the (electronic) computers. Various researchers propose solutions with the application of both apparent, and implicit schemes, “bound” to the relative frame front. “Binding” is made with a use of a method of rhythmic steps and “catching” of the front in a knot of a grid [8]. However, most of the numerical solution of Stefan’s problem the method of grids was widely adopted [5, 6, 8]. Along with questions about the creation of the solution of Stefan’s problems, its resolvability issues are important. The decision problem of a quasistationary task of the Stefan is substantially studied in works [8, 9]. Along with method of grids, big distribution in solvers of potent software products (for example, Star-CD, Ansys, Procast) was received by finite element methods and control volume.

In the finite element method, the domain in which the solution of differential equations is sought is divided into a finite number of subzones (elements). Coefficients of approximating functions are usually searched from the condition of equality of values of neighboring functions on the boundaries between elements (in clusters). From the point of view of computational mathematics, the idea of this method is that the minimization of the function of the variational problem is carried out on a set of functions, each of which is defined on a subdomain.

The method of control volume is successfully applied to an integration of the generalized equation of a mass heat transfer, including calculation of a gradient of size, sampling of a diffusion term, a sampling of a convective member, creation of a system of the algebraic equations. The method of control volumes has clear physical interpretation. The calculated area is divided into a finite number of control volumes in which barycentres nodal points have. Differential equations of conservation laws of weight, energy, a momentum integrate on each volume. Calculate integrals, being set by patch profiles of change of weight, energy, a momentum between nodal points.The method of control volumes allows, on the one hand, to solve parabolic, hyperbolic and elliptic problems, and with another – to use adaptive grids.

Earlier we developed the mathematical model of heat exchange in a twodimensional axisymmetric statement with the use of a numerical method of control volume on the basis of the Star-CD software product. The description of the mathematical formulation of the problem, which is a system of differential equations of continuity, conservation of momentum and conservation of energy, is presented in detail in [10]. As a result of carrying out a series of the numerical experiments necessary cooling rate of drops was determined by a research of a thermal condition of drops of a lead-bearing aluminum melt of various size in the course of their cooling in an aqueous medium at the fixed reference temperature of a melt.

In this paper, the algorithm for accounting for nonlinearity in the equations of transient thermal conductivity is refined, which allows for a numerical analysis of the influence of overheating of lead-containing aluminum melt droplets on their granulation process and to make the necessary adjustments to the approximate solution of the Stefan problem.

Mathematical model of the process

In general case Stephan’s problems can be considered as a problem of interfacing several temperature fields with special conditions on movable boundaries S , between them with defined boundary conditions. The temperature field of each i phase is defined by three dimensional differential equation of conductivity, where boundary coordinates satisfy the condition: S_{i -1}< ( x , y , z ) <  S i , i – 1,2,..., m.

If consider the task for two phases, the equation of Stephan’s problems on the boundary with thermal balance looks like this (indexes 1 and 2 refer to solid and liquid phase):

λ1∂T1x=ξ-λ2∂T2x=ξ=Lρdξ.

∂x         ∂xdτ

Here λ 1 and λ 2 are the thermal-conductivity coefficients of solid and liquid phase, (W/(m·K); L – hardening heat, kJ/kg; ρ – phase density, kg/m³; ξ – moving boundary (m) to the equivalent of τ, sec.

Thus, heat balance realisation requires heat L ρ d ξ to be equal to the difference to a quantity of heat which passed through borders ξ – x ₁ and ξ – x ₂. Also, heat spreading problem with the existence of phase transition and knowledge of the boundary phase speed comes down to solving a set of equations.

∂ T 1 _{= a} ∂ ² T 1 ∂τ ¹ ∂ x ²

0≤x≤ξ;∂T2=a∂2T2,0≤x≤∞.

∂τ 2∂x2

Here a ₁ and a ₂ are the thermal diffusivity coefficients for solid and liquid phases, respectively, m²/sec.

In classical Stephan’s problems, model crystallisation process with a constant temperature of the phase transition is considered T – const. Fluid mass x > – 0 is restricted from one side with the plane c x – 0. At the initial moment, τ – 0 liquid possesses constant temperature T . On the surface of x – 0 0

the temperature remains unchanged ( T (0, τ) – T s – const.). If T s <  T c , then the boundary condition of crystallisation x – ξ gets into a depth of liquid. The equations (2) are supplemented with boundary conditions: T 1 <  T s at x – 0; T 2 – T 0 at τ – 0. Furthermore, condition (1) is applied on the crystallisation border (at T 1 = T 2 – T c and x – ξ).

The given crystallisation solution values as limited nonlinear boundary problem, thermal characteristics and density are piecewise constant within each phase. And thermal capacity at T – T _c adopts infinitely big value, and phase changes occur instantly.

In Fig. 1 the accepted scheme of calculated area of hardening of drops of a melt at their driving is provided in an air and aqueous medium according to which the mathematical model of heat exchange of process of granulation is constructed. In a mathematical model process of crystallization at the fixed transition temperature of heat transfer is considered T c – const. Therefore Stefan’s condition on a demarcation of two phases (1) concerning the radius of a drop of R will be written as:

∂ξ ∂T

ρ L =λ when r =ξ ; T ( ξ , τ ) = T = const. ∂τ     ∂ r                          ^c

Thus, in the accepted two-phase calculated area Ω, divided into two subareas (fluid Ω^- and solid Ω⁺), on the border of S (τ) between them according to a condition (3) there is a rupture of a heat flux at the crystallization temperature of T _c (see Fig. 1). At the same time, the position of the displacement boundary S (τ) during hardening is clearly absent in the mathematical model, but is determined by the accepted condition T – T _c. According to [9] it the condition in the equation of energy is implemented with use by a δ-delta-function of Dirac when determining the size of efficient thermal capacity c eff ( T ). Then in case of T _sol – T _lig – T _c the shopping malls of the equation considering the warmth of phase change concentrated on the border by S (τ) take the following form [10, 11]:

c eff ( T ) = c p ( T ) + L δ (T-T с ).

Here δ-function receives values

{0, т > тс (1, т < тс.

It is visible that in the mathematical model the quasistationary Stephan’s problem characterized by the fact that in each separate subarea Ω- and Ω+ the thermal field is described by a differential equation of a transient heat conduction with internal sources of warmth is accepted. At the same time, the border of phase change is not mobile and unknown. In an axisymmetric frame, this equation takes a form

8Т I 8   сТ дТ дТ cρ∂T=1 ∂(rλ∂T)+∂T(λ∂T)+f,

∂τ r∂r    ∂r    ∂z ∂z where с is the specific heat, kJ/kg; f is the power of internal thermal emission, W/m3.

The equation (6) is a quasilinear parabolic second-kind equation as all coefficients in this equation are dependent on temperature. The environment of a particle was accepted by the homogeneous, i.e., coefficients in the equation (6) are functions only of temperatures.

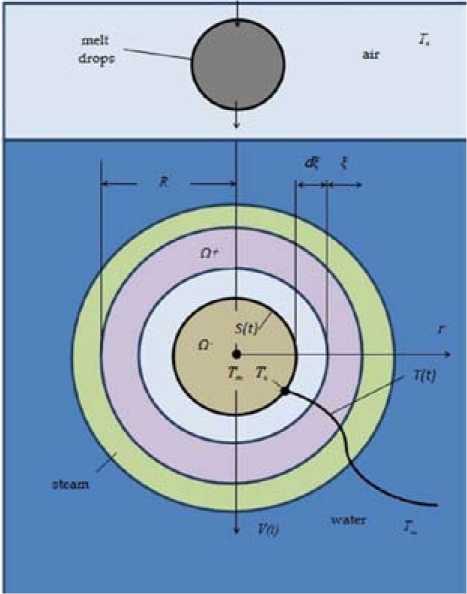
Fig. 1. Scheme of calculated area of hardening of drops of a melt when driving in an air and aqueous medium: R – drop radius; Ω^- and Ω⁺ – subareas respectively fluid (melt) and solid (crust); ξ – thickness of the hardened crust; S (τ) – border of phase change; v (τ) – travelingspeed of a drop; T a , T w , T m , T c and T (τ) – the temperature of air, water, melt, crystallization and at a given time, respectively

An important result of the solution of the simplified version of Stefan’s problems is receiving the simple ratio between the thickness of a solid crust and a cooling-off period which received the name “law of a square root” [2]:

t = K s ^, (7)

where ξ is the thickness of a solid crust of metal; τ is the time; K is the coefficient of a speed of a s crystallization (solidification constant), mm/τ0,5.

In engineering practice, the ratio (7) allows making a quick approximate assessment of thickness of a solid crust of metal in the course of its hardening. However, determination of the coefficient of K s is very difficult task. For some well-studied hardening processes, it is received empirically. Specification of the law of a square root is possible on the basis of the composite mathematical models. At the same time using possibilities of numerical methods and the modern software products, it is possible to consider and analyse influence practically of all factors accompanying metal hardening process.

Results and discussion

The main factor influencing the dynamics of solidification of melt droplets in an aqueous medium in the production of granules of a fixed size is its initial heating. In the theory of solidification of castings in order to approximate the model of solidification to real conditions, various modifications of the square root law (7) associated with the correction of the value of K S on the basis of empirical material have been widely used. However, from the point of view of practical use, they are not universal because of the significant, often insurmountable difficulties associated with determining the correction factors in the law of promotion of hard crust for each specific casting case. At the same time, the construction of an adequate approximate method for calculating the kinetics of crust growth taking into account the degree of overheating is associated with two key factors: the dynamics of heat exchange (changes in the heat transfer coefficient) in the system and the nature of the heat dissipation of the liquid phase overheating.

A calculated study of heat transfer in the process of granulation in an aqueous medium of melt droplets of composition Al-15% Pb (by weight) with a diameter of 4.5 was carried out...7.5 mm. The rate of solidification of the granules was estimated by the value of the initial overheating of the T m melt up to 1473 K. The temperature of the cooling water is T _w – 288 K. Note that the high value of the melt overheating adopted in the calculations is associated with a wide range of immiscibility temperatures of the liquid phase of the Al-Pb system [11].

The nature of the influence of the initial overheating of the melt on the solidification process of aluminum melt droplets is established. It was found that with increasing melt overheating, the rate of solidification decreases and practically does not depend on the size of the studied droplets (Fig. 2). The rate of formation of the solid phase in the initial stage is linear, and in the other-close to the parabola (Fig. 3).

In Fig. 4 the obtained dependence of the solidification constants of melt droplets with a diameter of 6 mm on the value of their overheating T m is given. As can be seen, the nature of the dependence is close to linear and, according to calculations, the ∆ К _s for the studied temperature range is on average 0.005 mm/sec.^0.5 on the 1 K to ∆ T m .

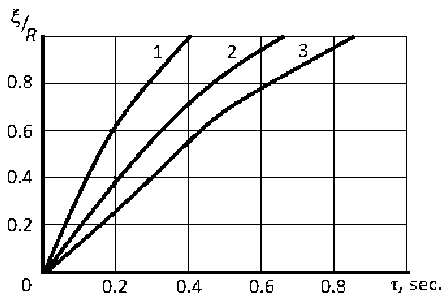
Fig. 2. Dependence of the relative thickness of the hardened crust ξ/ R of the melt droplet of different sizes on the time of movement in water τ: 1, 2 and 3 – droplet diameter 4.5; 6.0 and 7.5 mm

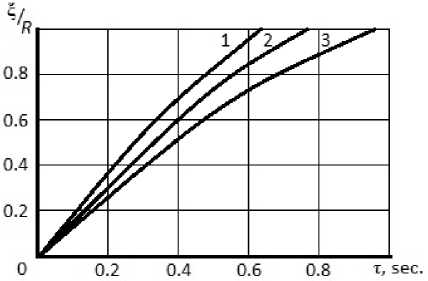
Fig. 3. Dependence of the relative thickness of the hardened crust ξ/ R on the overheating temperature of the melt droplet T m with a diameter of 6 mm: 1, 2 and 3 – 1373, 1423 and 1473 K

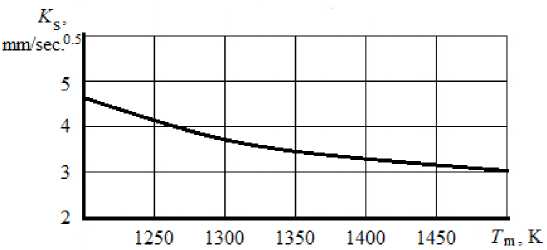
Fig. 4. Dependence of the coefficient of the rate of crystallization of a drop of melt K s with a diameter of 6 mm on the temperature of its overheating T m

Thus, an approximate engineering assessment of the solidification dynamics of lead-containing aluminum granules, taking into account their overheating, can be made on the basis of the following ratio:

ξ = [5.9 - (0.005 Δ T _m) τ .                                               (8)

Here ξ is the thickness of the hard crust of a metal drop with radius R (provided that ξ ≤ R ), mm; τ is the duration of the solidification process, sec.; ∆ T m is the temperature overheating (provided that T m >1.015 T c ), K.

Conclusions

• 1.    In the numerical model developed earlier the algorithm of calculation of process of solidification of liquid metal is improved, allowing to consider mobility of borders and heat of phase transition, nonlinearity of the equation of unsteady thermal conductivity.

• 2.    As a result of numerical studies, the character of the influence of droplet size and overheating of lead-containing aluminum melt on the dynamics of solidification of granules in air and water is established.

• 3.    The coefficient of crystallization rate (solidification) during granulation of melt droplets in a wide range of their overheating is determined.

• 4.    An approximate ratio is proposed that takes into account the amount of overheating of the liquid phase and connects the thickness of the formed solid phase with the duration of the granulation process.