Carrying out of effective recovery algorithms of distorted images

Currently, there is a wide use of optoelectronic spatial positioning of objects. In paper [1] the hardware and software implementation of optoelectronic system ranging shows the main approaches to solving problems related to accuracy in determining the distance to the object by using stereoscopic rangefinder created with two cameras running synchronously at different angles. Important part in

The task of image recovery is to improve the image quality on perception criterion obtained during image processing. Improving image quality is a subjective process, while the image recovery procedures are quite objective. The solution of recovery task is to reconstruct the image that has been distorted as a result of external influences, with sufficient a priori determined information. Therefore, the methods of image recovery are based on modeling interference occurring in the environment, and on using of appropriate algorithms for reconstruction of the original image. With this approach, it is necessary to formulate properly the quality criteria that will evaluate the result of recovery.

When solving the problem of image improving another approach is used based on the heuristic procedures, their results depend on the human vision. For example, contrast enhancement can be considered as a procedure of improving the image, as after its application the image becomes more pleasing to the eye, and the treatment of blurred images by use of corresponding inverse procedures should be referred to the set of tools of image recovery.

To carry out the simulation of image reconstruction algorithm there was used mathematical package MATLAB, which includes IPT library (Image Processing Toolbox) which contains the functions of digital image processing. Let us consider the basic approach used in the development of algorithms for the simulation of distortion and image recovery.

The deterioration of the image is modeled using the distortion function, which together with the additive noise creates a distortion of the «blurring» type. This function can be written as (1):

■                  ■                                                                                  (1)

where g (x,y) – image function, H – distorting operator, ξ (x, y) – additive noise, f (x, y) – initial spatial image function.

Formula (1) can be rewritten to the spatial domain as [2]:

g(x,y) =h(x,y)*f(x,y) + Kx,y),                                        (2)

where h (x, y) – space representation of distorting operator, «*» symbol – denotes convolution.

As it is known, convolution in the spatial domain is equivalent to multiplication in the frequency domain. Fourier transforms of these functions, so the above equation (2) of distortion model can be written in an equivalent representation in the frequency domain:

G(u, v) = H (u, v) + N (u, v) ,                                                      ⁽³⁾

where capital letters denote the corresponding Fourier transforms of functions of the convolution equation (2).

The function H (u, v) is often referred to as optical transfer function (OTF, Optical Transfer Function). The term is derived from Fourier analysis of optical systems [2]. In the spatial domain function h (x, y) is called the spread of points (PSF, Point Spread Function). This term occurs when the function h (x, y) reacts on the light points to produce distortion characteristics for various types of input data. Functions h (x, y) and H (u, v) transform into each other under the influence of forward and reverse Fourier transforms, so there are two M-function otf2psf and psf2otf for these actions in the MATLAB package.

In this paper the following algorithm to simulate the distorting function was used. Point Spread Function PSF was set by means of the operator fspecial IPT library as follows: PSF = fspecial (‘motion’, len, theta). Fspecial operator allows to simulate the effect of a linear movement of the camera relative to the fixed object, thereby allowing distortion of «blurring» type. Len parameter specifies the number of pixels that the camera was moving to, theta – is the angle parameter measured in degrees, and it is measured from the positive horizontal semi-axis counterclockwise. Motion parameter gives the transfer characteristic of the spatial filter, which, being folded with the image, approximates linear movement (camcorder with respect to the image) by len pixels. The direction of movement is defined by the value of theta angle.

To carry out the simulation of distortion of the «blurring» type the following parameters were used: len = 45, theta = 45. With using imfilter function there was developed the filter with transfer function given by PSF function. The filter allows to achieve the effect of blurring the image with a linear motion of objects. Further there was simulated the process of adding the additive Gaussian noise interference by IPT imnoise library functions. Gaussian noise has the following characteristics: zero mean value and variance equal to 0.01. Fig. 1 and 2 show the result of the model image distortion.

From Fig. 2 it is seen that such an image from a video camera is not suitable for further processing in the optoelectronic system for measuring distance, as the object itself and its borders are not distinguishable.

Let us consider the process of restoring the image after distortion shown in Fig. 2. The first step in recovery algorithm is a high-frequency filter that improves the image brightness and contrast. HF filter is projected with the help of prototype LF filter and has the following transfer characteristic h: h = ( ^— ^) * 1,2 . Where h 1 - transfer characteristic of the LF filter, which is HFF prototype.

The formula was obtained experimentally by the best image quality criteria, perceived visually. Next there was designed the filter to improve the image borders, based on the calculation of «counter harmonious average.» Further information connecting with such filtering techniques can be found in paper [2].

For the implementation of «counter harmonious average» filter IPT library function spfilt corresponds performing spatial filtering.

The final stage of restoring the image shown on Fig. 2 is the implementation of Lucy-Richardson algorithm giving the biggest effect in case of distortions discussed in this paper. Lucy-Richardson recovery algorithm is the algorithm of non-linear iterative reconstruction [2]. Let us consider the algorithm. Lucy Richardson algorithm is based on a maximum likelihood method, in which an image is formed using the Poisson statistics [2]. Maximization of the likelihood function model leads to an equation that has a solution for the next iteration of convergence, as in formula (4):

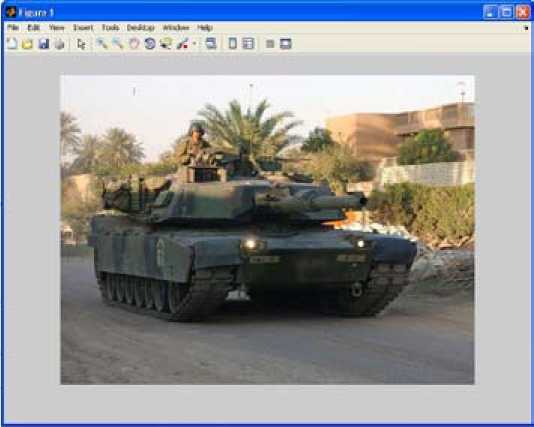
Fig. 1. The original image

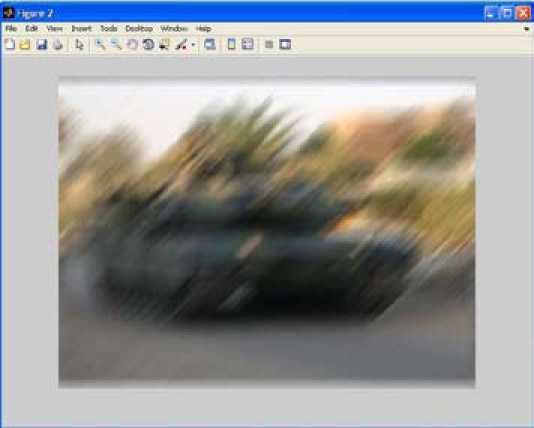
Fig. 2. The result of the model introducing distortion

Mv) = f K (x-y) [h(-x,-y) .;-g;g-] ,                (4)

n(x,y)*ik(x,y)

where the symbol «*» denotes convolution, fk – k – approximation tainted image and functions f, g are identified.

IPT library has this algorithm performed by deconvlucy function with the following syntax: deconvlucy (g, PFS, NUMIT, DAMPAR, WEIGHT), where g – distorted image, PFS – spread function points, NUMIT – the number of iterations, DAMPAR – a scalar that specifies the deviation limit of the received image of g. Iterations stop for pixels which deviation from the initial values does not exceed – 639 –

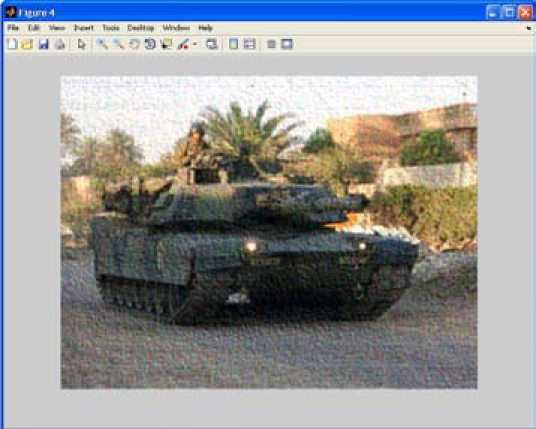
Fig. 3. The result of Lucy-Richardson algorithm this limit. This prevents the generation of noise in such pixels preserving necessary details. While default DAMPAR = 0 (no limit stop), WEIGHT – an array with the dimension of g, which assigns each pixel some weight that reflects its quality.

For example «bad» pixels derived from the defective area on the image can be excluded from consideration giving them zero weight.

To implement Lucy-Richardson algorithm there were taken the following parameters: NUMIT = 80 (the number of iterations is chosen experimentally for the case) DAMPAR = 0 (no limit stops), the parameter WEIGHT – set default. The result of the final stage of recovery after arithmetic average is shown in Fig. 3.

Fig.3 shows the result of image reconstruction using algorithms proposed by the authors in the paper and it is acceptable for further processing in the optoelectronic system ranging [1], as the reconstructed image has clear borders and it is possible to identify the object itself. Using the above said algorithms the authors of the paper created iterative model program.

The result will be useful in the development of electronic identification systems and range finders both in military industry and civil sectors: in television, robotics and automation industry. The disadvantage of this algorithm is relatively large processing time, so the authors are continuing the research to reduce the processing time and to study the possibilities of morphological features of image processing algorithms.