Categorization in Unsupervised Generative Self-learning Systems

Published Online June 2021 in MECS DOI: 10.5815/ijmecs.2021.03.06

In a number of previously published results [1,2,3], an interesting effect was observed: exposing certain models of unsupervised learning, such as autoencoder neural networks, to large sets of real-world data, with no supervision in training, or in fact, any other form of a prior knowledge of the semantics or content, the law, parameters and characteristics of distribution, similarity relationships, etc. under certain conditions may lead to the emergence of a concept-sensitive structures in the representations created by the model. This effect will be called unsupervised concept categorization.

• A.    Literature Review

In a number of works in the recent years important connections were established between several principles proposed as the foundation of machine learning: the principle of Bayesian inference and methods based on it [4]; the principle of minimization of free energy in energy-based learning [5,6]; and the bottleneck principle [7].

An important conclusion from these results for unsupervised learning is the equivalence of these principles in application to training of models with self-encoding and regeneration. Specifically, it follows from these results that models trained with Bayesian methods such as commonly used stochastic gradient methods [8] to minimize the loss of regeneration of the original data will also produce, as the consequence of the equivalence [4], configurations with the lowest free energy of the learning model. This observation is important because energy parameters of the models and characteristics of distributions in the representations created by such models can be closely related

An important application of these principles in self-learning systems that do not depend on extensive prior knowledge of the domain are unsupervised models with self-encoding and regeneration, of which autoencoder models represent a subclass. A general structure of such models is illustrated in Fig.1.

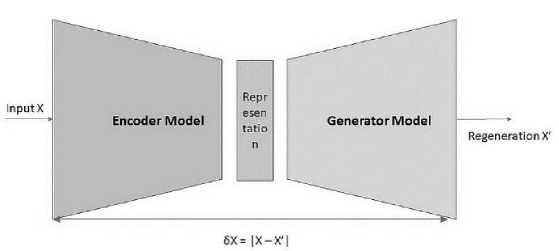
Fig.1. Self-encoding generative model

Characteristic for these models is the presence of two essential components: the encoder, that performs transformation from the space of input, or observable data to the representation space of the model; and the generator that reproduces, or generates an image in the observable space from a representation sample. The process of unsupervised, or self-supervised training then attempts to reduce the cost function of the difference between the original distribution and its regeneration by the model.

Well-known examples of such models are Restricted Boltzmann machines and Deep Belief Networks [9,10] as well as autoencoder neural networks [11,12,13]. In the latter models the encoding and generating components are combined into a single feed-forward network, with a training process for both encoding and generative parts based on minimization of the deviation of regenerated distribution form the original one via one of the loss backpropagation methods, such as stochastic gradient descent methods [14,15] and others.

In the experimental field, a number of significant results in unsupervised learning have been obtained as well. In Le et al. [1], a massive deep and sparse autoencoder model was trained with a large array of images (over 10 million of raw images) with the observed effect of the emergence of concept-sensitive neurons activated by images in a certain higher-level concept without any prior knowledge of the content or semantics of the data.

In [2], a spontaneous formation of grid-like navigation cells, similar to those observed in mammals was detected in navigation modeling experiments with a recurrent neural network with deep reinforcement learning.

The emergence of a higher-level concept correlated structure (unsupervised information landscape) was observed directly in [3] in representations created in unsupervised learning by deep autoencoder models with Internet via visualization of concept distributions in the representation space.

In addition, a substantial improvement in the performance of supervised classification with features obtained with different models of unsupervised learning (unsupervised feature learning) has now become a common practice in machine learning [16-18].

These results, observed in independent studies with data of different types and nature may spark a question: is the effect of native categorization in unsupervised learning coincidental with specific models or learning scenarios, or can in be caused by some underlying principles of processing information that can be common for a range of learning systems, both artificial and biologic.

• B.    Problem Statement

While the effect of unsupervised categorization by higher-level concepts was observed in several works previously, there is not yet a clear understanding of its nature and the underlying cause, nor is it clear whether it is specific to the reported experiments or has more general applicability. For these reasons, investigating and understanding the nature of this effect can be of interest and significant benefit to the field of unsupervised machine learning and general learning.

Based on the empirical observations cited above the hypothesis of the study can be formulated as follows:

Unsupervised Categorization Conjecture : training of unsupervised models with self-encoding (from observable space to representation) and regeneration (from representation to the observable space) with a training procedure compliant with the principle of Bayesian inference and satisfying the conditions of constant accuracy; generalization; and compression; statistically prefers representations with better geometrical categorization of hidden concepts in the representation created as a result of training.

Proving the conjecture would be of interest for several reasons. Importantly, it would provide a theoretical foundation for the effect of unsupervised categorization observed in several previously published works; as well it would explain the improvement in classification performance after pre-processing of data with unsupervised feature selection.

And not in the least, it could offer insights for a natural mechanism of formation of abstract higher-level concepts as a result of training with optimization of generative capacity of self-learning models.

• C.    Methodology

• 2.    Theoretical Analysis of Unsupervised Categorization

In the research we use theoretical analysis of the geometrical parameters of distributions in the representations of unsupervised models created in unsupervised training with minimization of generative deviation from the perspective of minimization of generative error and free energy function.

In the experimental section of the work we present the results of experiments in self-learning with unsupervised representations, comparing them with raw, unprocessed input data. Both theoretical and experimental results provide strong support for the hypothesis of the study.

We will begin the approach to the proof of the unsupervised categorization conjecture with some key definitions.

• A.    Definitions

Data : general input data is parametrized by observable parameters {x_i} in the observable space X. In unsupervised training models create representations of the observable data parametrized by the representation parameters (or coordinates) {r i } in the representation space R.

Hidden (or native) concepts : we will consider the case where the data contains significant presence of similar (in certain, unknown to the model explicitly way) samples from the set of hidden concepts { H k } possibly with some contribution of non-categorized data, or noise. Note that neither of: the set of hidden concepts; the relationship of similarity for any such concept; distribution characteristics of concepts H k or any other prior knowledge about the hidden concepts is not available to the models before or in the process of unsupervised training.

Categorization : by good geometric categorization in the representation space is meant the pattern of distributions of hidden concepts in the representation space where concept regions are compact and well-separated from each other, that is, 1) the average size / volume of a concept region is minimized:

Vol(H i ) -> min (1)

and 2) the overall volume of the overlap between different concept regions:

O = ∑ O ij = ∑R(H i )∩ R(H j )→ min (2) B. Categorisation in Supervised Learning

Supervised learning is a special case of general learning where the set of concepts in the observable data is known a priori as classes, and models are trained to match the prediction to a pre-known label with a variety of common methods.

In this approach classification can be considered as a case of explicit categorization and a lemma stating that the conditions of good classification and categorization by the known set of classes are equivalent can be proven:

Lemma 1 (of supervised categorization ): if a well-categorized representation of data D can be achieved by a certain model M 0 for the given set of classes { C }, then there exists a model M 1 with a matching accuracy of classification from D into { C } and vice versa.

Proof : According to the definition, if a categorized representation of D exists and provided by a certain model M 0 the class distribution regions {C R } in the representation space R represent compact and separated set of manifolds in R. Then, according to the results on universal approximation of feed-forward neural networks [19], there exists a neural network M’ that maps class distribution regions {C R } to the set of classes {C} with any given accuracy A . An example of such a network though may not be the minimal or most efficient one, is a multi-dimensional step function approximation.

Then, by adding the feed-forward networks M0 and M’ output-to-input as (M0, M’) one can obtain a mapping of the original data D to the set of classes {C} with the matching accuracy and the proof of the first part of the lemma is complete.

The second part is then straightforward: if a model M 1 exists that maps D to {C} with a given accuracy, then it the classification transformation T: D ^ {C} itself can be considered as a well-categorized representation of D, and the representation space R in this case will be identical to the space of known classes {C}.

Thus, the statements of good classification and good categorization into a set of pre-known classes follow from each other in the case of supervised leaning models and therefore, are equivalent.

A proof of the similar statement in the case of unsupervised learning, that is, without preliminary knowledge about the set of concepts in the data is less straightforward. Nevertheless, under certain assumptions and conditions, for selfencoding-regenerating models with forward propagation, it can be shown that the constraints of good accuracy of reproduction of the original data D and compression in the space of representation as well as the requirement of strong generalization, that is, independence of the accuracy of regeneration from a particular set of data in models with

Bayesian training would result in a statistical preference of representations with good categorization in the set of hidden concepts with significant representation in the observable data.

• C.    Preliminary Arguments

To illustrate the approaches to the proof of the conjecture, let us first consider two boundary scenarios. In the first scenario suppose that hidden concept distributions are well categorized to compact and dense regions separated from each other. We will use the manifold assumption [20], i.e. that the concept distributions in the observable parameter space are represented by a finite number of continuous manifolds. This assumption can be justified in commonly studied examples such as the distribution of human faces, that represents though complex, but rather continuous region in the space of all images.

In this case as can be seen immediately, the dispersion of a hidden concept in the representation space will be small in the scale of the representation space , v(h) ≪ G, G being the characteristic size of the representation space.

Importantly, the generative mapping from the concept region to its image in the observable space under the stated assumptions can be relatively simple and can be modeled with a finite neural network that are effective in approximation of continuous and smooth distributions.

Next, we note that knowing the distributions of hidden concepts in the representation space and the generative transformation is sufficient to regenerate the part of the data that belongs to hidden concepts. In this case, one can conclude that both components of the regeneration transformation, i.e. the representation distribution and the generative mapping to the observable space have low variation and can support the constraints of good accuracy of regeneration (that is limited only by the fraction of general, non-categorized noise) and generalization simultaneously, that is, the accuracy of regeneration can be maintained across datasets of any size and with any number of installments, as long as the nature of data does not change significantly.

In the best case of a very strong categorization, the regenerative mapping for a given concept can be represented by a single point-to-point function – from the center of the concept cluster in the representation space (a representation prototype or “template” of the concept) to its image in the observable space, the observable prototype, possibly with some local variation that constitutes the manifold of the observable concept region. Such a template mapping would be effectively defined by

N reg = D rep + D obs ~ D obs , (3)

(as in the case of significant compression, D rep ≪ D obs ) parameters, where D rep and D obs are the dimensionalities of the representation and the observable (i.e. input data) spaces, respectively.

Interesting to note that just such a strategy has been known for a long time in the domain of criminological facial reconstruction. Decades of experience confirmed that the wide range of variations of a general human face can be successfully described by only 20-50 parameters (such as facial feature categories) with a relatively small number of discreet values in each, an enormous compression compared to the resolution of a human eye (approx. 580 megapixels by 7 million colors). These observations, as well as results reported in the earlier studies [1-3] provide a direct experimental confirmation of the conjecture of unsupervised categorization.

Turning to the second boundary scenario, let us consider the opposite case, where the resulting representation regions of hidden concepts are spread over the entire representation space and overlap significantly. Clearly, the representation component of the regenerative transformation for the concept data in this case would have higher variance: d spr ~ G ≫ d cat in the first example.

Consequently, the mapping from the concept regions in the representation space to different continuous manifolds representing concept images in the observable space will need to be more complex and variable to maintain the desired accuracy of regeneration, as close samples belonging to essentially different concepts would need to be mapped to different concept manifolds in the observable space. This complexity would translate into higher number of parameters in the generative function requiring more complex approximation with greater number of independent parameters than in the first example.

In the end, this scenario cannot be compatible with the constraints of accuracy and generalization imposed simultaneously. Indeed, with each new set of data the density of samples of essentially different concepts in the same region of the representation space would increase continuously meaning that more and more complex approximations would be needed to map different regions in the observable space with a stable accuracy. Eventually, either the accuracy constraint would need to be foregone, if the complexity of the model could not be increased any further; or the generality of the model would deteriorate, and a new set of data may cause the accuracy to drop.

These examples illustrate two essential points: first, that representations with better categorization can be simpler and for that reason, have lower regeneration loss and energy configurations of the regenerative model; and secondly, that only well-categorized representations can support true generalization that is, the regeneration accuracy maintained over the data sets of any size and regardless of the volume or number of new installments as long as the character of the data remains stable.

In the formal proof of the categorization conjecture we shall use the argument that the configurations with the best categorization also minimize the loss of the trained model. We will use already discussed observation that the resulting regeneration of the input data in a trained model is controlled by two sets of factors: those of distributions of hidden concepts in the representation space of the model; and those that define the generative transformation from the representation to the observable space. Hence, the functions of the configuration of the model such as the loss, and free energy are also defined by these factors that will be referred to as “regenerative configuration” of the model:

L = L(H,g-),E = E(H,g)

• D.    Categorized Representations Minimise Loss

We can now proceed with the proof of the following lemma:

Lemma 2 (of minimum loss ): if a regenerative configuration with the best categorization of hidden concepts exists in the representation created by a self-encoding-regenerative model with Bayesian training to minimize the error of regeneration, it is also the configuration with the lowest average loss among the regenerative mappings of the given learning model.

Proof : Suppose that the representation distribution of a hidden concept H_k is controlled by distribution parameters h_k in the representation space such as a set of coordinates of k-dimensional clusters or manifolds. Then,

R = U H_k + N

where N is the random noise component not associated with any hidden concept. Recall again that hidden concepts are not known to the model explicitly, neither before nor in the process of training.

As well, we consider the parameters g i of the generative model from the representation space to the observable space, such as weighs and biases:

F_ge^. R -> I; F_gen = F(_Qi)

Suppose that for a trained Bayesian model there exists a regenerative configuration that maximizes the categorization of the distributions of hidden concepts {H_k} in the representation space, that is, minimizes the size of the distribution area of H k and maximizes its separation from regions occupied by other hidden concepts.

Next, allow for a small variation of configuration parameters for H k , p k = {δh k , δg j } and evaluate the corresponding differential of the regeneration loss function ∂L⁄∂p.

Starting with the distribution parameters { h k } one can remark that if the region of representation is increased in one dimension, while the model parameters remain constant, some samples outside of the initial concept region can be mapped to a different area in the observable space potentially increasing the error of mapping placing the observable image in the wrong concept “class”; also more samples of different “foreign” concepts can be now present in the extended concept region δH_k, and as well mapped to a wrong concept region in the observable space, increasing the false positive or statistical type 1 error, and consequently, the total error of regeneration.

One can observe, as illustrated in Fig.2, both channels can be a potential source of an increase in the regeneration error compared to the initial state.

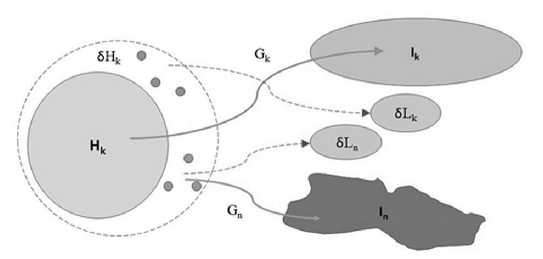
Fig.2. Sources of variational error, distribution parameters

Hence, it follows that:

8L(H, g) _> Q

8hk

Now let us consider variations of the model parameters G ={gi}, with hidden concept distribution parameters fixed. Recall that the model parameters of the starting configuration with Bayesian learning already minimizes the regeneration loss so any variation in the model parameter values should increase the loss in the observable space and therefore, the energy of the regeneration function:

8L(H, g) > _Q

9gi    ""

From (7) and (8) one can readily conclude that for all regenerative configuration parameters { p } it holds:

8L(H, g) > Q dp   — from which follows that the configuration with the best categorization also minimizes the regeneration error of the model thus completing the proof of the lemma.

The proof of the unsupervised categorization conjecture then follows immediately from (9) and the results on the equivalence of the principles of Bayesian learning and minimization of free energy and on stochastic gradient methods as approximation of Bayesian training.

Indeed, from the just proven lemma that categorized representations minimize the regeneration loss in training of models with self-encoding and regeneration; and that the configurations with minimal loss are produced by training with stochastic gradient descent methods proven to be an approximation of Bayesian learning [8]; and from the equivalence of Bayesian learning and minimum energy principle [4] it follows that categorized representations also minimize free energy of the model and will be preferred statistically as a result of unsupervised Bayesian training to minimize the regenerative error of the model.

To conclude, one needs to note first the essential assumptions and limitations that will be discussed in the next section; the other essential note is that the statistical preference of categorized representations does not mean that every training process that satisfy the conditions of the unsupervised categorization theorem would produce a well-categorized representation. Rather, that in an ensemble of learning systems under the aforementioned constraints of the theorem, the learners with categorized representations would be statistically preferred outcome of training. This observation can and was indeed verified in the experiments with learning models where in a number of learning runs one could see individual learners showing statistical variations in their performance, while certain average level is maintained (Section III, C).

• E.    Assumptions and Limitations

In the proof, a number of implicit assumptions were made which we are going to discuss and attempt to justify in this section.

The first point is the existence of categorized representations. In the proof it was implicitly assumed that a configuration with the best categorization exists in the space of all possible regenerative configurations. It is believed that cited experimental results, as well as empirical experience with practices of face recognition provide support and justification for this assumption.

The second important assumption is the significance of the observable parameters. Indeed, the observable parameters have to be relevant and specific enough to differentiate between samples of essentially different hidden concepts. Consider a simple example: let the face images dataset used to train a deep learning model have only one parameter, for example, gender of the person. Clearly, the only possible categorization in this case could be by the value of the gender parameter.

An important consideration is the representation of hidden concepts in the dataset. Artificially constructed sets can create disbalance between hidden concepts that could affect training of the model and the resulting representations. As well, the populations of hidden concepts must be sufficiently large to establish characteristic structures in the representation of the learning model.

Finally, it has to be noted that the condition of compression is essential to avoid the identity transformation counter-example that is achievable by neural network models if the effective dimension of the representation space is greater or equal to the dimensionality of essential parameters (i.e. those responsible for significant variation) in the input data.

• F.    Categorisation and Generalization

• 3.    Experimental Support for Unsupervised Categorization

The results of the study into categorization properties of hidden concept distributions in the representations of regenerative models can offer insights into the relation between the conditions of accuracy and generality in both supervised and unsupervised learning scenarios. A question can be asked, to what minimal dimensionality limit can a given data be compressed to still provide effective learning that is, satisfy both requirements of accuracy and generality simultaneously?

Compression of the observable data to a categorized representation can provide significant reduction in the energy of the regenerative mapping due to reduction of dimensionality in the representation space that affects the effective degrees of freedom. This gain may extend all the way to the limit where the dimensionality of the representation space would reach that of the local variation in the representations of hidden concepts with the highest population in the data, i.e. the number of independent parameters, or degrees of freedom in the variation of hidden concept distributions Hk.

Beyond that limit the constraints of accuracy and generality could not be maintained simultaneously: forcing the model to sustain accuracy would make it overfit that is, encode the training data literally without categorization; while an attempt to train such a model with larger sets of data would affect the accuracy, of classification in supervised learning or regeneration in unsupervised models.

Thus, it can be hypothesized that the optimal effective dimension of the representations in models with selfencoding and regeneration can be chosen based on the expected or observed variation spectrum in the native concepts of the data, that in some cases can be approximated by certain known higher-level concepts.

In addition to already cited results offering experimental support for the effect of categorization in unsupervised learning, a set of experiments was conducted with real neural network regenerative models (deep stacked autoencoder) to provide convincing evidence for the theoretical results presented in the previous section as well as the impact of unsupervised categorization on the efficiency of learning.

• A.    Purpose of the Experiment

The purpose of the experiment was to compare the efficiency of self-learning, measured as the accuracy of classification of the learned concepts in the initial, unprocessed data space and in the representation obtained with an unsupervised encoder trained to reduce the generative error. The difference in classification accuracy between classifiers trained with the same sample in the input data space and representation space should give a clear indication about the effectiveness of categorization by higher-level concept in the representation created by the model in unsupervised training.

The null hypothesis (that is, no significant effect of unsupervised categorization in the experiment) would manifest itself as the absence of a clear difference in classification accuracy for the concept being learned between the classifier trained with a signal sample in the input data space vs the one trained with the image of the same sample in the representation.

However, if the hypothesis of unsupervised categorization is correct, the outcome of the experiment should see a significant improvement in the learning efficiency measured by the accuracy of classification, between the cases of raw, unprocessed input data and the structured representation created in unsupervised training.

Clearly, in measuring the accuracy the errors of both statistical types need to be taken into account.

• B.    Experimental Setup

The model used in the experiment is a stacked two-stage deep autoencoder. The model produced two stages of representations of unprocessed aerial image data. The model and the dataset are described in detail in [21].

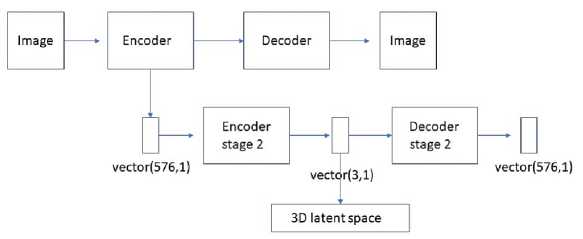
Fig.3. Deep stacked autoencoder model

In the experiment, six out of ten labeled classes in the dataset were used in self-learning; however, the rest of the data was still used as uncategorized background to verify the resolution of the resulting learning. The classes used in self-learning were the following: buildings; woods; fields; water; roads; large construction structures (classes 1 – 6 below, respectively).

The encoder of the first stage was a convolutional-pooling autoencoder that produced a numerical representation of a dimension 576 from color images with dimensions (64,64) to (128,128). The resulting representation was used as an input to the second stage encoder with physical dimensionality reduction to 3 dimensions:

(128 х 128 х 3)^ (576,)^ (3,)

The dimension of the final representation stage was chosen according to the results of the principal component analysis that indicated three principal dimensions with combined weight of above 95. The maximum compression of information achieved by the encoding process was thus in the range of 16,000.

In the process of unsupervised training the models have achieved significant improvement in all measured metrics. Loss, mean squared error (MSE) and mean absolute error (MAE), decreased by a factor of 102 after 50-100 epochs of self-supervised training; while cross-categorical accuracy, that is a measure of covariance of the input and output samples has increased from below 1% to approximately 35%. Such an improvement in regeneration performance of a trained unsupervised feed-forward model signifies that it has indeed learned and retained essential information about the input data that allows to regenerate it efficiently in the regenerative stage despite considerable compression in the representation layer.

To investigate the impact of the unsupervised categorization on the learning capacity of models, an unsupervised structure of density clusters was identified by applying a density clustering method, such as MeanShift [22] in two sets of data: 1) the original, input dataset and 2) its representation created by a pre-trained generative model described earlier in this section. Then, a landscape-based method of signal sample learning described in [3] was applied with the resulting cluster structure in the input data and its low-dimensional representation created by the model.

The signal sample method unsupervised self-learning of new concepts with a single true sample is based on marking the cluster(s) associated with the signal sample and producing an artificial labeled concept dataset generated from the unsupervised cluster structure identified as a result of unsupervised learning phase, that can be used to train the initial iteration of the binary classifier of the concept. As demonstrated, even with a single true sample of the concept a trained classifier can learn to identify it in the input data with the accuracy significantly better than random.

• C.    Experiment Results

The classification results of a trained classifier for a concept in in raw (that is, unprocessed input data) and representation by a trained model were measured in a set 100 tests with 100 randomly selected samples of in- and out-of-concept each, thus 20,000 predictions in total for each of the measured concepts. The accuracy was measured as a combination of the recall and false positive rate, representing statistical errors of types 2 and 1, and a combined accuracy measure, F1, that incorporates the errors of both types. The mean and best accuracy scores as well as standard deviation (SD) as a measure of statistical variation were calculated for each concept over 10 learning experiments.

The results of the self-learning experiments are presented in Table 1.

Table 1. Concept Self-Learning Accuracy

Concept	Accuracy, Representation (Mean)	Representation F1 (Best / Mean)	Representation F1 (SD)	Accuracy, Input (mean)
Class 1	0.679 / 0.330	0.700 / 0.677	0.018	0.95 / 0.76
Class 2	0.868 / 0.373	0.741 / 0.727	0.007	1.00 / 0.75
Class 3	0.958 / 0.275	0.842 / 0.824	0.021	1.00 / 0.75
Class 4	0.515 / 0.425	0.556 / 0.543	0.007	1.00 / 0.76
Class 5	0.654 / 0.375	0.656 / 0.637	0.010	1.00 / 0.77
Class 6 *	0.889 / 0.394	0.743 / 0.720	0.020	1.00 / 0.77

*With adjusted learning parameters: number of initial samples, cutoff for out-of-concept clusters [2]

To remind, the null hypothesis in this experiment would be represented by one of the following outcomes: 1) a failure of the representation classifier to learn, i.e. a strongly biased prediction to acceptance, or rejection; or 2) the accuracy of the representation classifier on the level of a random prediction i.e. for a binary classifier, (½, ½) or F1-score of 0.5.

As can be seen from the results above, while classifiers in the representation space for all measured concepts were able to achieve signal accuracy better, and in most cases significantly better than the random threshold, those trained with samples in the input space were not able to converge to a meaningful resolution, and remained strongly biased for acceptance (in some cases, a bias for rejection was observed as well). In over 100 learning experiments across all measured concepts, the null hypothesis has not been observed, with the resulting statistical significance of the support for the effect of unsupervised categorization better than 99%.

It is worth noting that the accuracy results in the input space were observed in the entire range of the bandwidth parameter of the density clustering method as confirmed by a grid search in the entire range of its variation, and therefore the presented results cannot be attributed to a specific choice of parameters.

A logical conclusion from these results is that the density structure or “unsupervised landscape” in the representation that develops in unsupervised learning via minimisation of regenerative error proves essential for successful learning of new concepts with minimal data that can only be the case if it is closely correlated with common concepts in the input data.

D. Visualization

The results of the experiments in the previous section can be illustrated by direct visualizations of the concept distribution regions in the low-dimensional representation space of a pre-trained regenerative model.

Presented in Fig. 4 are the reconstructed surfaces of the concept distribution regions obtained with triangular interpolation of concept samples encoded by the model into the representation space.

In the diagram above, from top left, clockwise: concepts 1 (lighter) and 2; concepts 3 and 4 (lighter); concepts 5 and 6 (lighter); the last diagram, bottom right, illustrates the scale of the compact concept distributions (concepts 3 and 6) in the coordinates of the representation space.

As can be seen in the visualizations, for most studied concepts distribution regions in the latent space were represented by smooth and compact low-dimensional manifolds supporting the accuracy results presented in the previous section, as signal learning training sets for concepts being learned generated artificially based on the signal sample and the unsupervised landscape in the representation can be expected to be effective in the case of such compact and well-defined distributions in the latent space.

Fig.4. Concept distribution regions in the representation space

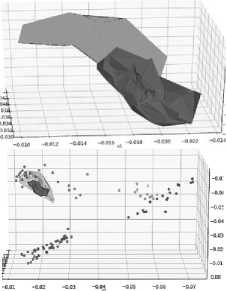
Importantly, these results also validate the manifold assumption commonly used in unsupervised and semisupervised machine learning [20]. The structure and distributions of the concepts in the representations of models with regenerative self-learning will be investigated in more depth in future works.

• 4.    Conclusions and Discussion

In this work theoretical approaches in the analysis of unsupervised representations were introduced with the proof of the conjecture of unsupervised categorization that links categorization properties of unsupervised distributions in representations of models with self-encoding and regeneration, and Bayesian training to minimize the error of regeneration.

In Section III experimental results were presented that, along with cited previously published results of other independent studies provide strong empirical support for the effect of unsupervised categorization observed with data of different types and origin.

On the basis of theoretical and experimental results presented in this work, as well as those reported in the earlier studies, one is led to conclude that the hypothesis of the study that is, the effect categorization by native concepts in unsupervised generative learning has a general character, being a consequence of the general principles of information processing in systems satisfying the identified conditions and constraints in the process of unsupervised generative learning.

The results of the study can have significance for the field of unsupervised machine learning because unsupervised categorization can offer a natural platform for development of flexible and environment driven learning strategies in the settings where massive amounts of labeled data used in common approaches aren not readily available. This specifically applies to new domains and environments where domain knowledge is scarce and large amounts of verified data are not yet available.

The connection between unsupervised training and concept-sensitive structure in the representations may offer valuable insights about the emergence and modeling of intelligence that can be common for artificial and biologic systems. Indeed, it can be remarked that the natural, biologic systems known for their capacity to learn independently, with minimal supervision or prior knowledge as noted by Hassabis et al. [23], “human cognition is distinguished by its capacity to rapidly learn about new concepts from only a handful of examples” also commonly apply the same constraints of accuracy of reproduction of the observable data; generalization; and compression that were used in the hypothesis of unsupervised categorization in this study. Further linking the results of this work with a number of recent results in biological neurocomputing, is the observation of low dimensional representations similar to those observed in the experimental results in Section III that appear to play an important role in processing of sensory information in human brain [24,25].

Thus, the conclusions about the general character of the effect of unsupervised categorization in generative learning can offer an important link between learning processes of biologic systems and used as a basis for development of approaches and methods in self-learning and general learning systems that are flexible, interactive, iterative, and require minimal supervision or prior knowledge about the domain [26].

Acknowledgment

The authors wish to thank the colleagues at the Department of Information Technology, National Aviation University, and Network Engineering, Solana Networks for valuable discussions about the topics in this work and a number of helpful comments.