Cauchy problem solution for a hyperbolic system of the homogeneous 2-dimensional quasilinear equations

Among hyperbolic systems of the nonlinear equations with partial derivatives the systems of the quasilinear equations of two independent variables, are most studied. These systems in particular describe the unsteady onedimensional and the supersonic two-dimensional stationary flows of compressible gases and liquids, two-dimensional deformed plastic state of continuous medium, etc. A lot of them are reduced to a hyperbolic system of homogeneous quasilinear equations ux + A( u, v) uy = 0,

V x + B ( u , v ) V y =0, (1) where u = u ( x , y ), v = v ( x , y ), an indices the lower meaning of the derivation with respect to the corresponding variables. This kind of system can be linearized by applying a so-called hodograph transformation if and only if the corresponding Jacobian is not equals to zero in some domain of solution existence.

From the other hand, the conservation laws [1] are one of the fundamental characteristics of any mechanical process. In the section 2 we have described a method of analytical solving of boundary-value problems for the system (1). This method is based on the use of conservations laws of systems under consideration. The main features of the presnted method consist of the possibility of problem linearization without considering the singularity of Jacobian transformation to obtain exact solutions for boundary-valued problems in explicit form.

In section 3 we consider the application of this method to some exact systems of the bi-dimensional plasticity mathematical theory.

Conservation Laws. Let us set Cauchy’s problem for the system (1): in something like an arc a < т <  b of a smooth curve L

L = {(x,У):x = x(т),y = y(т),те[a,b]} in the plane xOy it is required to find a solution of the system (1), that takes given values on L u (x, У) I L = u (x (т), У (т)) = u 0(т),

^{v ( x} , У ) | l = ^{v ( x ( т )}, У ^{( т ))} = ^v ° ^{( т )}.

The characteristics equations of the system (1) look like dxdx =A, dydy

with the relations in the characteristics u = u ⁰ , v = v ⁰ equally.

A conservation law of the equations set (1) is searched in the form of the relation

C x + D y =0,                  (3)

where C = C ( u , v ), D = D ( u , v ) should vanish from all solutions of the system (1):

^C u u x ^{+ C} v v x ^{+ D} u u y ^{+ D} v ^V y =

= - AC^ - BC v V y + D_цU y + D^ =0, hence

D_tt - AC =0, D v - BC v =0.          (4)

Equation (3), if the conditions of Green’s theorem are satisfied, is equivalent to a relation

J - Cdy + Ddx = 0,

Г where Г is an arbitrary smooth closed contour.

In the plane xOy we have considered the closed path MNK , where M ⁽ x m ⁽ a ), У т ⁽ a )), N ⁽ x „ ⁽ b ), У п ⁽ b )) ^е L , K ( x_k , y_k ) is the point of an intersection of characteristics v = v ⁰, u = u ⁰, drawing through the points M , N respectively.

Then,

J - Cdy + Ddx = J Ddx - Cdy +

MNK             MN

+ J Ddx - Cdy + J Ddx - Cdy = 0.        ⁽⁵⁾

Taking into ^NK account expre ^K ss ^M ions (2)

J Ddx - Cdy = J ( D - AC ) dx = NKNK

= x ( D - AC )| xk - J x d _v ( D - AC ) dv .

Similarly,

J Ddx - Cdy = J ( D - BC ) dx = KMKM

= x ( D - BC ) | xm - J x a _u ( D - BC ) du .

Let us put the following coKMnditions dv [(D - AC )| 0,,^     =

L                  ^u = ^{u ( x (} b ) у ⁽ b )) J

= 0, a„[ ( d - bc )| ₀         1 = 0.          (6)

L                    v = v ( x ( a ), y ( a )) J

Let us denote

ф ( u , v ) = D - AC , v ( u , v ) = D - BC .

Then

D = ( A v- B ф )/( A - B ), C = ( у-ф )/( A - B ), where A * B , because the considered system (1) is a hyperbolic one and has two different characteristics.

In the new variables, the system (4) has the form ф u + K 1(V-ф) = 0,

V v + K 2 ( у-ф ) = 0,               ⁽⁷⁾

where K 1 = A u /( A - B ); K 2 = B_v /( A - B ).

Conditions (6) we shall take as follows ф | = 0 = Const1 = 1, v I = 0 = Const2 = 0.      (8)

Coming back to (5) and taking into account (8), we shall obtain

[ Ddx - Cdy = - ( x ( D - AC ) | xk + x ( D - BC ) | xm ) = x _n x _k

MN

^{- (} x k ^ф |    0

u = u

, v = v ⁰

^- x n ^ф |    0 ⁺ x m V | 0

u = u            v = v

= x n ^- x k .

^- x k ^V L = u 0, v = v 0 ) =

If we find a solution of the linear system (7), that satisfied the boundary conditions (8), then we shall define the coordinate x_k from the equation (9).

On the other hand, for y-coordinate dy =

NK

NK

ф

= y —

A

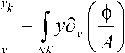
dv .

n

Similarly, dy =

KM

KM ym

v

= y — в

-

KM

y _k

Let’s assume d v

A

u = u ⁰ ( x ( b ), y ( b )) ^_

d

v

^B v = v ⁰ ( x ( a ), y ( a ))

=0,

=0.

The conditions (10) we can note are the following ф |u=u0 = A(u0, v), V |v=v0 = 0.              (11)

From (5) taking into account (10) we have

ф

Ddx - Cdy = - y_k —

MN                           u = u ⁰ , v = v ⁰

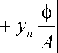
The solution of the problem (7), (11) makes possible to find the coordinate y_k from the equation (12). Thus, we shall define the coordinates of the point K , where the values of the functions u , v can be restored.

Let us notice, that the same steps can be applied for the Riemann problem [2].

Examples of applying the method. In this work [3] we have found all the conservations laws of the bi-dimensional plasticity system under the Sent-Venan–Mises yield criterion:

• □    _x - 2 k ( 9 _x cos 2 9 + 9 _y sin 2 9 ) = 0,

• □    _y - 2 k ( 9 _x sin2 9-9 _y cos2 9 ) = 0,         (13)

where □ is the hydrostatic pressure; 9 is the angle between the first main direction of a stress tensor and the ox -axis; k is a constant of plasticity. Here we have described the special class of conservation laws that are used for solution for Cauchy problem system (13).

The system (13) in the form (1) looks like this:

^L x ^{+ L} y tg ⁹ = ^0, П x ^-П y Ctg ⁹ = ^0, where 2 9 = n-L □ = k ( n + L ). The solution of the problem (7), (8) has a form ф = p /cos 9 , V = 2 p_L /sin 9 where:

P ^{( L} n ) = R ^{( L} Lp n , n 0 ^)cos

[ n ^-L i

I 2 J

1 ⁿ                 ^t-L. ^

• - - JR(L Lp n, T)sinI —° IdT-22 n0                      vy

Accordingly, the solution of the problem (7), (11) is:

p ^{( L} , n ) = R ^{( L} Lp n , n 0 ^)sin ^0 2 ^ ^⁺

• 1    ⁿ                 ^t-L, ^

• +    - JR(L Lp n, T)cos II

22 n0                      vy where R(Ln,^0,n0) = I0 (V(L-L0)(n-n0)) is the Bessel function of the zero order of an imaginary argument; I0(0)=1,I0'(0)=0.

The generalization of (13) shows that it is a system of ideal plasticity equations under Coulomb’s yield criterion of the form:

• □    _x (1 + cos 2a cos 20) + □ _y cos 2a sin 20 =

= 2( ct cos 2a + k sin 2a)(0 _x sin 20 - 0 _y cos 20),

• □    _x cos 2 a sin 2 0 + □ _y (1 - cos 2 a cos 2 0 ) =

= -2(a cos 2a + k sin 2a)(0x cos 20 + 0y sin 20), where n/2 - 2a is a constant angle of internal friction; 0 = 9 +n /4 . If a = n /4. Then we have the system (13). In the system described above there is a stress state of granular materials.

This system in the form (1) looks like this:

L x +L y tg (0-a) = 0, nx -n y tg (0 + a) = 0, where L = 2tg 2a ln(a ctg 2a + k) -0;

n = 2tg 2 a ln( a ctg 2 a + k ) + 0 . The solution of problem (7), (8) has a form [4]:

ф = y ( -L , -n ) ^ ( L , n )/ cos( 0 - a ),

Y ( L , n ) = exp( - ( L + n )/2ctg 2 a ),

V = y ( L 0 , n 0 ) R ( L L 0 , n , n 0 )cos ( ( n 0 -L 0 )/2 -a ) -

Z n0

x[ sin ( ( t-^ ₀)/2 -a ) - ctg 2 a cos ( ( t-^ ₀)Z 2 -a ) ] d t .(14) The solution of the problem (7), (11) is:

V = Y(^o, По)R(i -, П, По ) sin ((По - I 2 -a)

• -    2 J R & ^ o , n, T)y(^ o , t ) X

• ^{2 n}o

x[ctg 2a sin ( ( t-^₀ )/ 2 -a ) - cos ( ( t-^₀ )/2 -a ) ] d t , (15) where R (^, п , ^ o ,П о ) = I о (V (^-^ o )(n-n o )/sin2a ) . From the equation (9) taken into account (14) we have discovered coordinate x_k . Using (15), and from equations (12) we have received coordinate y_k . This way, we have determined point K , in which the values of functions ^, n are restored.

The bibliographic list

• 1.    Symmetries and conservation laws for differential equations of mathematical physics : мonograph / A. V. Bocharov, V. N. Chetverikov, S. V. Duzhin, et al. Amer. Math. Soc., 1999.

• 2.    Senashov, S. I. The solving of the main boundary problems of plasticity by means of conservation laws. Modern Group Analysis VII, Developments in Theory, Computation and Application / S. I. Senashov, A. N. Yakhno. Norway : MARS Publishers, 1999. P. 149–154.

• 3.    Senashov, S. I. Simmetries and conservation laws of 2dimensional ideals plasticity / S. I. Senashov, A. M. Vinogradov // Proc. Edinburg Math. Soc . 1988. Vol. 31. P. 415–439.

• 4.    Kiriakov, P. P. Applications of symmeties and conservation laws for solution of differential equations / P. P. Kiriakov, S. I. Senashov, A. N. Yakhno // Publ. of Siberian Branch of Russian Academy of Science. 2001. (In Russian).

• С. И. Сенашов, А. Яхно

РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ГИПЕРБОЛИЧЕСКОЙ СИСТЕМЫ ОДНОРОДНЫХ ДВУМЕРНЫХ КВАЗИЛИНЕЙНЫХ УРАВНЕНИЙ

Описан метод решения граничных задач для гиперболической системы однородных квазилинейных уравнений двух независимых переменных с применением законов сохранения. Этот метод применяется к задаче Коши для системы двумерной пластичности с условием Сен-Венана–Мизеса, а также для системы с условием Колумба.