Cellular Automata based Encrypted ECG-hash Code Generation: An Application in Inter human Biometric Authentication System

Автор: Subrata Nandi, Satyabrata Roy, Jayanti Dansana, Wahiba Ben Abdessalem Karaa, Ruben Ray, Shatadru Roy Chowdhury, Sayan Chakraborty, Nilanjan Dey

Журнал: International Journal of Computer Network and Information Security(IJCNIS) @ijcnis

Статья в выпуске: 11 vol.6, 2014 года.

Бесплатный доступ

In this modern era, biometrics incorporate various mechanisms to recognize inimitable features of human beings by utilizing their biological and evident features. This paper proposes a novel technique for constructing a resilient and secure biometric recognition system. In this paper, an ECG-hash code of two distinct individuals has been formed by taking dot product of electrocardiogram (ECG) feature matrices of two persons located at two different sites at respective databases. The validity of the system increases as samples from both persons, between whom the transmission takes place, are essential. Besides, electrocardiogram is such a unique feature of an individual that could not be compromised at any circumstance as contradictory to other features like fingerprints, face recognition etc. Moreover, the ECG-hash code is encrypted using rule vector of cellular automata that gives better security in terms of randomness of generated cipher text.

Еще

Inimitable, electrocardiogram, dot product, cellular automata, ECG-hash code, randomness, cipher text

Короткий адрес: https://sciup.org/15011354

IDR: 15011354

Текст научной статьи Cellular Automata based Encrypted ECG-hash Code Generation: An Application in Inter human Biometric Authentication System

Published Online October 2014 in MECS

This era is characterized by expeditious growth in terms of communication and exchange of information over wireless channels that tend to be highly insecure. It gives rise to an authentication mechanism so that operational data and/or electronic transactions do not go in wrong hands unintentionally. The essence to authenticate the receiver on the other hand is very crucial for preserving integrity and confidentiality of the sent information. Capacity of human brain falls short in memorizing passwords and/or IDs that are among the most popular way of authentication now-a-days. Besides, due to the erroneous practice of human beings, sometimes they forget to carry those credentials or these credentials may be stolen or copied. So, biometric devices that use unique traits of individuals like fingerprints, face recognition, retina scan etc. have started to become useful as they use inherent features of a person. But these systems have certain limitations. When a person ages or gets some injuries, then these types of systems tend to fail giving faulty outcome. But ECG and EEG are among the features that survive from these limitations due to their inherent mechanism. The process of biometric authentication consists of two steps - a) enrollment and b) verification [19]. In enrollment step, a template is produced after taking out the required features from an individual's biometric data. Verification process is the way of generating a new template from a user's biometric data after a raw scan and matching it with the previous one [1]. The person is authentic if and only if the value of essential parameters after comparison lies within a previously defined threshold value.

In general, there are two ways to achieve biometric authentication e.g. uni-modal [2], [3] and multi-modal [4], [5]. False acceptance rate (FAR) and false rejection rate (FRR) are the two parameters that measure the performance of a biometric system [1]. Equal error rate (ERR) is when these two parameters become same. Mathematically, ERR = (FAR+FRR)/2. A biometric system is perfect when the value of ERR is zero [6]. As mentioned above, biometric systems have some limitations. When it goes to an intruder [4], data privacy is violated. A person's retina and fingerprints changes with time. Solution of the problem is cancelable biometrics [5]. Cancelable biometrics is more secure as it is non invertible and it can be reused [1]. So it does not demand to be kept secret [7]. But this non invertible transform is not said to be non-vulnerable. This gives birth to bio-hash, which is also a form of cancelable biometrics [8]. This bio-hash is obtained by performing dot product of the biometric feature of a person in some iterations and a tokenized random number provided by user. This is the process of extracting feature matrix from an individual's biometric feature. So it provides better security as both the random number and the particular biometric feature is required to crack it. Moreover, this system has zero error rate point [ERP] [8].

II. Motivation

In this work, electrocardiogram (ECG) has been used as a biometric feature due to its uniqueness.

ECG is a tool to diagnose the presence of any abnormality in the heart of any individual and is based upon the electrical activities of heart. ECG is unique and depends on physical configuration especially that of the chest of any individual. Therefore it can be used to uniquely identify any person. A standard ECG for a single cardiac cycle is shown in Fig. 1.

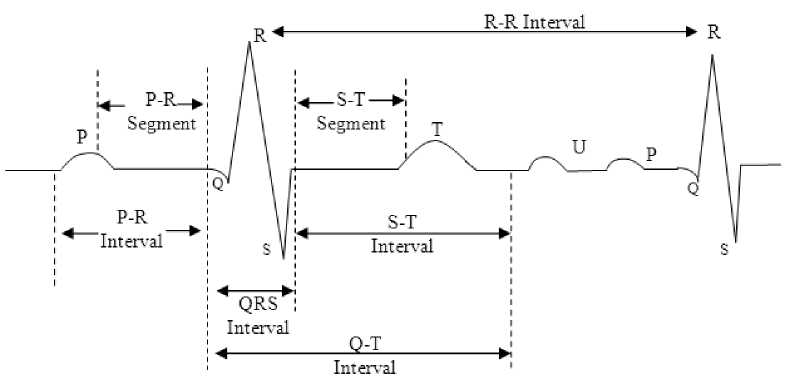
Fig.1. P-QRS-T complex detected ECG signal [1]

Fig. 1 contains a P-wave, a QRS complex, a T -wave and a U-wave [8].

In this current work, a dot product is performed between ECG feature matrices, obtained from two different individuals, from two remote sites. The use of more than one characteristic in multimodal approach does not stop any user from being authenticated even if one trait fails because the others are still used to match. But, the major limitation is that the characteristics obtained are from a single entity. There are approaches where the biometric sample is obtained from two individuals [1]. Since ECG feature is unique and it is obtained from two individuals, it gives better security than multimodal approach. In this paper one more security issue has been added. The newly generated ECG-hash code is further encrypted using rule vectors of cellular automata.

Recent studies suggest that many characteristics of cellular automata can be used efficiently to achieve essential cryptographic criteria i.e. balanced, correlation immune, non-linearity etc. CA can also be used to generate balanced and high quality rules that consist of various radiuses [9] and to generate pseudo random number [10]. CA can also be used to generate random cipher text in symmetric key cryptographic purpose as reported in [11]. Here, the same technique as of [11] is applied to encrypt the ECG-hash code before transmission. This gives more security because of three issues: a) ECG signal [20] is unique b) biometric feature matrix is obtained from two individuals and c) the ECG-hash code is encrypted using CA rule vector before transmission.

III. Basic of Cellular Automata

A. Cellular Automata

Cellular automata are an array of cells capable of storing one bit at a time. Each cell transits into a new state at next timestamp depending on the states of its neighbors and a transition rule [11]. So cellular automata can be defined by three tuples (S, T, N), where S is the non empty finite set of states, T is the non empty finite set of transition rules, and N is the non empty finite set of neighbors. CA was invented by J. v. Neumann [12] and was popularized by S. Wolfram [13]. For example, consider 2 states, 3 neighborhood one dimensional CA. The first row represents all possible cell values of three cells at timestamp t. Next row onwards represent the state of the current cell at timestamp t+1. Here we consider current cell as i, the left hand neighbor as i-1 and right hand neighbor as i+1.

Table 1. Example rules for next state update

Rule No	111	110	101	100	011	010	001	000
51	0	0	1	1	0	0	1	1
60	0	0	1	1	1	1	0	0
102	0	1	1	0	0	1	1	0
153	1	0	0	1	1	0	0	1
195	1	1	0	0	0	0	1	1

T is conventionally represented as characteristic matrix of CA that is composed of rules of all cells. It is an n×n (for n cells) matrix constructed according to the rule for individual cell. j-th row stands for a rule applicable to the j-th cell. If its next state is based on a particular cell, then its position in matrix T is marked by '1' , otherwise it is marked by '0'. The state transition is mathematically represented as: [ p₊^x ) ] = [ r ]_x[ p ( x ) ] , where P t+i (x) is the state of cell i at t+1 timestamp and P_t(x) is the state of cell i at timestamp t. The rules can be represented as follows:

Rule 51: P ₊ 1 ( x ) = P ( x )

Rule 60: P t + 1 ( x ) = P t ( x ) © P t ( x - 1)

Rule 102: P t ₊ ₁ ( x ) = p ( x + 1) © P t ( x )

Rule 153: P ₊₁ ( x ) = P ( x + 1) © P ( x )

Rule ¹⁹⁵ P_t + 1 ( x ) = P ( x ) © P_t ( x - 1)

There are total 256 such rules of one dimensional cellular automaton [11]. The CAs can be of many types viz. additive, non-additive, periodic boundary, null boundary, programmable CA, Group CA etc. as reported in [14].

B. Group Cellular Automata

A cellular automaton is called group cellular automata when it regenerates the initial bit string after a certain number of iteration after application of a particular rule vector. Mathematically,

[ 7 ] n = I ( I is the identity matrix)

[P+n (x)] = [r]n x[P (x)]

where, n denotes the order of the group[15].

We can have 256 combinations when rule 51 and 102 are applied [11]. Out of these 256 combinations, <11000011> is preferred where 1 denotes rule 51 and 0 denotes rule 102. The order of the group cellular automata used in this work is 8. So, ECG-hash code is encrypted in 4 iterations using the above rule vector and applying the same vector, in next 4 iterations the encrypted ECG-hash code is decrypted.

The block diagram of the proposed system is given below:

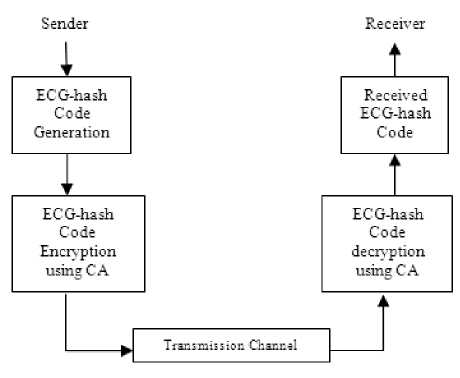
Fig.2. Block diagram of overall system

A. Generation of ECG-hash Code

Step 1. Modified Pan-Tompkin's algorithm [16][17] is applied on ECG signal to detect P, QRS, and T components.

Step 2. ECG features like R-R, P-P, Q-Q, S-S, P-R, and Q-T is measured from the ECG signal whose peaks are detected.

Step 3. A matrix of dimension 8x32 is generated based on the features detected from ECG.

Step 4. Dot product is performed between two matrices, one of sender and another of receiver, that is stored in the sender's database (DB1).

Step 5. The product is compared with the threshold value set beforehand/a priori. If the value exceeds the threshold then set this to binary 1 otherwise it is reset to 0.

Step 6. The newly generated ECG-hash code is sent to CA encryption system.

B. Encryption of ECG-hash Code using CA

The input to this encryption system is a binary ECG-hash code of length 32. We divide this into four 8-bit blocks. Then the following algorithm is applied.

Step 1. An 8-bit block is fed into programmable cellular automata.

Step 2. A rule vector <11000011> is applied to each cell, where 1 represents CA rule 51 and 0 represents CA rule 102.

Step 3. The PCA is run for four consecutive clock cycles.

Step 4. Encrypted plaintext or cipher text is generated.

Step 5. Step 1 to step 4 is repeated until remaining 3 blocks are encrypted.

Below is the block diagram of generating encrypted ECG-hash code.

IV. Proposed System

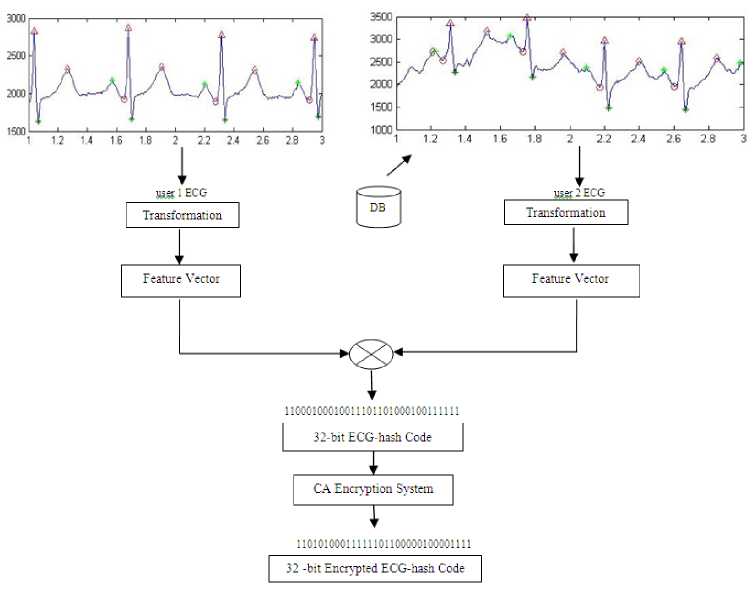
Fig.3. Encrypted Hash Code Generation

C. Decryption of encoded ECG-hash code on Receiver

Input to this encryption system is the encrypted binary ECG-hash code of length 32. We divide this also into four 8-bit blocks. Then following algorithm is applied.

Step 1. A single 8 bit block is fed into programmable cellular automata.

Step 2. A rule vector <11000011> is applied to each cell, where 1 represents CA rule 51 and 0 represents CA rule 102.

Step 3. The PCA is run for four consecutive clock cycles.

Step 4. Encrypted plaintext or cipher text is generated.

Step 5. Step 1 to step 4 is repeated until remaining 3 blocks are encrypted.

Fig. 4 is the block diagram of the decryption of ECG-hash code using CA.

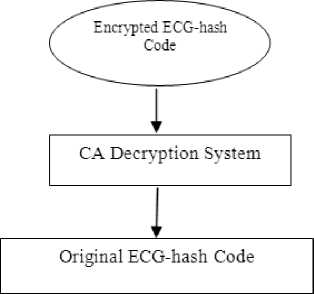
Fig.4. Decryption of encrypted ECG-hash Code

Fig. 5 below describes the encryption of first 8 bits of 32-bit ECG-hash code using cellular automata rule vector <11000011> as mentioned in the algorithm.

<51 51 102 102 102 102 5151>

1 1 0 0 0 1 00

0 0 0 0 1 1 11

1 1 0 1 0 0 00

0 0 1 1 0 0 11

110 10 100

Fig. 5. Encryption of the first 8 bits of generated 32-bit ECG-hash Code

Fig. 6 below depicts the decryption of first 8 bits of 32 bit ECG-hash code.

<51 51 102 102 102 102 5 51>

110 10 100

0 0 111111

1 1 0 0 0000

0 0 0 0 0011

1 1 0 0 0 1 00

Fig. 6. Decryption of first 8 bits of 32 bit ECG-hash Code

V. Results

In this work, we have used Matlab 7.0.1 to perform ECG-hash code generation and for comparative analysis purpose. We have used Dev C++ 4.9.9.2 to apply cellular automata encryption and decryption algorithm and obtaining result. In table 2 through 5, we have tabulated the time duration for P-P, -Q, R-R, T-T, P-R, Q-T, and Q-Tc, ORS of user 1.

Table 2. P-P and Q-Q time intervals

Sl. No.	Interval	Time Intervals (sec)	Interval	Time Intervals (sec)
1	P-P	0.6400	Q-Q	0.6300
2		0.6450		0.6550
3		0.6300		0.6250
4		0.6350		0.6400
5		0.6250		0.6000
6		0.6200		0.6500
7		0.6250		0.6150
8		0.6000		0.6000
9		0.6200		0.6000
10		0.6050		0.6350
11		0.6250		0.6250
12		0.6250		0.6000
13		0.6300		0.6450
14		0.6500		0.6200
15		0.6300		0.6550
16		0.6200		0.6050
17		0.6250		0.6250
18		0.6200		0.6400
19		0.6300		0.6150
20		0.6300		0.6250
21		0.6050		0.6050
22		0.6300		0.6350
23		0.6400		0.6300
24		0.6300		0.6500
25		0.3300		0.2600
26		0.4200		0.5000
27		0.6400		0.6300
28		0.6450		0.6550
29		0.6300		0.6250
30		0.6350		0.6400
31		0.6250		0.6000
32		0.6200		0.6500

Table 3. R-R and T-T time intervals

Sl. No.	Interval	Time Intervals (sec)	Interval	Time Intervals (sec)
1	R-R	0.6450	T-T	0.6450
2		0.6400		0.6400
3		0.6350		0.6350
4		0.6300		0.6400
5		0.6250		0.6200
6		0.6250		0.6200
7		0.6150		0.6100
8		0.6100		0.6100
9		0.6150		0.6200
10		0.6100		0.6100
11		0.6250		0.6200
12		0.6250		0.6350
13		0.6250		0.6300
14		0.6450		0.6350
15		0.6350		0.6400
16		0.6250		0.6200
17		0.6200		0.6200
18		0.6200		0.6250
19		0.6250		0.6250
20		0.6250		0.6250
21		0.6200		0.6100
22		0.6250		0.6300
23		0.6300		0.6300
24		0.6400		0.6350
25		0.2250		0.1700
26		0.5250		0.5850
27		0.6450		0.6450
28		0.6400		0.6400
29		0.6350		0.6350
30		0.6300		0.6400
31		0.6250		0.6200
32		0.6250		0.6200

Table 4. P-R and Q-T time intervals

Sl. No.	Interval	Time Intervals (sec)	Interval	Time Intervals (sec)
1	P-R	0.1100	Q-T	0.2550
2		0.1150		0.2700
3		0.1100		0.2550
4		0.1150		0.2650
5		0.1100		0.2650
6		0.1100		0.2850
7		0.1150		0.2550
8		0.1050		0.2500
9		0.1150		0.2600
10		0.1100		0.2800
11		0.1150		0.2550
12		0.1150		0.2500
13		0.1150		0.2850
14		0.1100		0.2700
15		0.1050		0.2850
16		0.1100		0.2700
17		0.1150		0.2850
18		0.1100		0.2800
19		0.1100		0.2650
20		0.1050		0.2750
21		0.1000		0.2750
22		0.1150		0.2800
23		0.1100		0.2750
24		0.1000		0.2750
25		0.1100		0.2600
26		0.0050		0.1700
27		0.1100		0.2550
28		0.1150		0.2700
29		0.1100		0.2550
30		0.1150		0.2650
31		0.1100		0.2650
32		0.1100		0.2850

Table 5. Q-Tc and QRS time intervals

Sl. No.	Interval	Time Intervals (sec)	Interval	Time Intervals (sec)
1	Q-Tc	0.3175	QRS	0.0550
2		0.3375		0.0700
3		0.3200		0.0550
4		0.3339		0.0650
5		0.3352		0.0600
6		0.3605		0.0800
7		0.3252		0.0550
8		0.3201		0.0550
9		0.3315		0.0650
10		0.3585		0.0800
11		0.3226		0.0550
12		0.3162		0.0550
13		0.3605		0.0800
14		0.3362		0.0600
15		0.3576		0.0850
16		0.3415		0.0650
17		0.3620		0.0850
18		0.3556		0.0850
19		0.3352		0.0600
20		0.3479		0.0700
21		0.3493		0.0700
22		0.3542		0.0850
23		0.3465		0.0750
24		0.3438		0.0750
25		0.5481		0.0650
26		0.2346		0.1300
27		0.3175		0.0550
28		0.3375		0.0700
29		0.3200		0.0550
30		0.3339		0.0650
31		0.3352		0.0600
32		0.3605		0.0800

In table 6 through 9, we have tabulated the time duration for P-P, -Q, R-R, T-T, P-R, Q-T, and Q-Tc, ORS of user 2.

Table 6. P-P and Q-Q time intervals

Sl. No.	Interval	Time Intervals (sec)	Interval	Time Intervals (sec)
1	P-P	0.4200	Q-Q	0.3850
2		0.4900		0.5200
3		0.4300		0.4600
4		0.4400		0.4450
5		0.4450		0.4250
6		0.4400		0.4400
7		0.4600		0.4600
8		0.4300		0.4300
9		0.4400		0.4500
10		0.4500		0.4600
11		0.4500		0.4450
12		0.4500		0.4500
13		0.4450		0.4300
14		0.4500		0.4650
15		0.4650		0.4550
16		0.4500		0.4450
17		0.4550		0.4700
18		0.4550		0.4550
19		0.4550		0.4350
20		0.4650		0.4650
21		0.4300		0.4500
22		0.4450		0.4450
23		0.4400		0.4400
24		0.4550		0.4350
25		0.4400		0.4450
26		0.4400		0.4400
27		0.4500		0.4550
28		0.4550		0.4500
29		0.4350		0.4450
30		0.4700		0.4450
31		0.4350		0.4650
32		0.4550		0.4450

Table 7. R-R and T-T time intervals

Sl. No.	Interval	Time Intervals (sec)	Interval	Time Intervals (sec)
1	R-R	0.4500	T-T	0.5900
2		0.4500		0.3150
3		0.4450		0.4350
4		0.4450		0.4400
5		0.4450		0.4450
6		0.4400		0.4600
7		0.4450		0.4250
8		0.4450		0.4650
9		0.4400		0.4400
10		0.4500		0.4450
11		0.4500		0.4450
12		0.4450		0.4450
13		0.4500		0.4500
14		0.4500		0.4500
15		0.4500		0.4450
16		0.4600		0.4600
17		0.4550		0.4600
18		0.4550		0.4450
19		0.4550		0.4650
20		0.4500		0.4500
21		0.4450		0.4400
22		0.4500		0.4500
23		0.4450		0.4500
24		0.4450		0.4400
25		0.4400		0.4450
26		0.4450		0.4450
27		0.4450		0.4400
28		0.4450		0.4450
29		0.4500		0.4500
30		0.4550		0.4500
31		0.4500		0.4550
32		0.4500		0.4500

Table 8. P-R and Q-T time intervals

Sl. No.	Interval	Time Intervals (sec)	Interval	Time Intervals (sec)
1	P-R	0.0950	Q-T	0.2550
2		0.1250		0.4600
3		0.0850		0.2550
4		0.1000		0.2300
5		0.1050		0.2250
6		0.1050		0.2450
7		0.1050		0.2650
8		0.0900		0.2300
9		0.1050		0.2650
10		0.1050		0.2550
11		0.1050		0.2400
12		0.1050		0.2400
13		0.1000		0.2350
14		0.1050		0.2550
15		0.1050		0.2400
16		0.0900		0.2300
17		0.1000		0.2450
18		0.1000		0.2350
19		0.1000		0.2250
20		0.1000		0.2550
21		0.0850		0.2400
22		0.1000		0.2300
23		0.1050		0.2350
24		0.1100		0.2450
25		0.1000		0.2500
26		0.1000		0.2500
27		0.1050		0.2550
28		0.1000		0.2400
29		0.0900		0.2350
30		0.1050		0.2400
31		0.0900		0.2450
32		0.1050		0.2350

Table 9. Q-Tc and QRS time intervals

Sl. No.	Interval	Time Intervals (sec)	Interval	Time Intervals (sec)
1	Q-Tc	0.3801	QRS	0.0700
2		0.6857		0
3		0.3823		0.0700
4		0.3448		0.0550
5		0.3373		0.0500
6		0.3694		0.0650
7		0.3973		0.0700
8		0.3448		0.0550
9		0.3995		0.0700
10		0.3801		0.0650
11		0.3578		0.0500
12		0.3598		0.0550
13		0.3503		0.0500
14		0.3801		0.0700
15		0.3578		0.0550
16		0.3391		0.0600
9		0.3995		0.0700
10		0.3801		0.0650
11		0.3578		0.0500
12		0.3598		0.0550
13		0.3503		0.0500
14		0.3801		0.0700
15		0.3578		0.0550
16		0.3391		0.0600
17		0.3632		0.0650
18		0.3484		0.0500
19		0.3336		0.0500
20		0.3801		0.0700
21		0.3598		0.0550
22		0.3429		0.0500
23		0.3523		0.0500
24		0.3673		0.0550
25		0.3769		0.0700
26		0.3748		0.0700
27		0.3823		0.0750
28		0.3598		0.0600
29		0.3503		0.0550
30		0.3558		0.0650
31		0.3652		0.0700
32		0.3503		0.0550

Now for user 1: The means of selected attributes for consecutive peaks are: Mean₁=1.3468, Mean₂=1.3293, Mean 3 = 1.3322, Mean 4 = 1.2238 etc.; where each mean is considered as the threshold value (T) for its respective block.

We have got first block of the Keymatrix 1 as shown below:

0.6400 0.6450 0.6300 0.6350 0.6250 0.6200 0.6250 0.6000

0.6300 0.6550 0.6300 0.6250 0.6400 0.6000 0.6500 0.6150

0.6450 0.6400 0.6350 0.6300 0.6250 0.6250 0.6150 0.6100

0.6450 0.6400 0.6350 0.6400 0.6200 0.6200 0.6100 0.6100

0.1100 0.1150 0.1100 0.1150 0.1100 0.1100 0.1150 0.1050

0.2550 0 2700 0.2550 0.2650 0.2650 0.2850 0.2550 0.2500

0.3175 0.3375 0.3200 0.3339 0.3352 0.3605 0.3252 0.3201

0.0550 0.0700 0.0550 0.0650 0.0600 0.0800 0.0550 0.0550

Fig.7. Keymatrix1

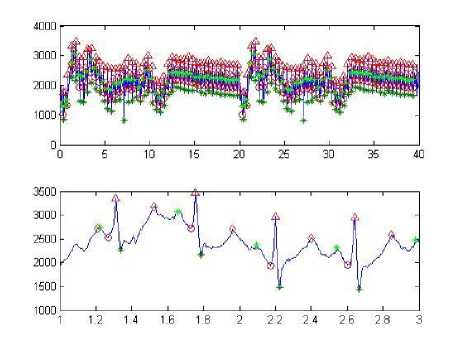
Fig.9. Signal and peak detection of user 2

Here is how we have gone through the process of extraction of feature matrix. There are total of four 8-bit blocks of Keymatrix1 and Keymatrix2.

Similarly, we have got the

first block of the

Keymatrix2 as shown below:

0.4200 0.3850

О 4500 0.5900 0.0950 0.2550 0.3801 0.0700

0.4900

0.5200

0.4500

0.3150

0.1250

0.4600

0.6857

0.4300

0.4600

0.4450

0.4350

0.0850

0.2550

0.3823

0.0700

0.4400

0.4450

0.4400

0.1000

0.2300

0.3448

0.0550

0.4450

0.4250

0.4450

0.1050

0.2250

О ..33 73

0.0500

0.4400

0.4600

0.1050

0.2450

0.3694

0.0650

0.4600

0.4450

0.4250

0.1050

0.2650

0.3973

0.0700

0.4300

0.4450

0.4650

0.0900

0.2300

0.3448

0.0550

Fig.8. Keymatrix2

Original and cropped ECG signal from user 1 and user 2 are shown in the Fig. 8 below:

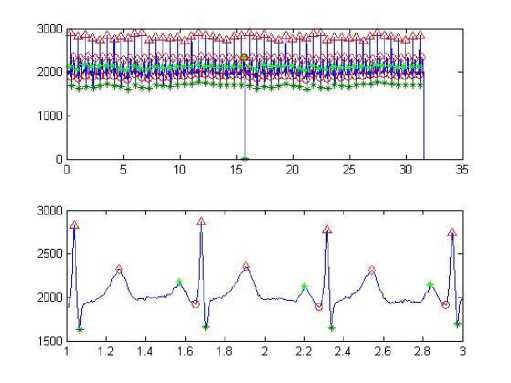
Fig.8. Signal and peak detection of user 1

From User 1

Block Bi .......................... BlockBj

0.6400 0.6450 0.6300 0.6350 0.6250 0.6200 0.6250 0.6000

0.6300 0.6550 0.6300 0.6250 0.6400 0.6000 0.6500 0.6150

0.6450 0.6400 0.6350 0.6300 0.6250 0.6250 06150 0.6100

0.6450 0.6400 0.6350 0.6400 0.6200 0.6200 0.6100 0.6100

0.1100 0.1150 0.1100 0.1150 0.1100 0.1100 0.1150 0.1050

0.2550 0.2700 0.2550 0.2650 0.2650 0.2850 0.2550 0.2500

0.3175 0.3375 0.3200 0.3339 0.3352 0.3605 0.3252 0.3201

00550 0.0700 0.0550 0.0650 0.0600 0.800 0.0550 0.0550

From User 2

Block B'i .................................. Block BO

0.4200 0.4900 0.4300 0.4400 0.4450 0.4400 0.4600 04300

0.3850 0.5200 0 4600 0.4450 0.4250 0 4400 0 4600 04300

04500 0.4500 0.4450 0 4450 0.4450 0 4400 0 4450 0.4450

0.5900 0.3150 0.4350 0.4400 0.4450 0.4600 0.4250 0.4650

0.0950 0.1250 0.0850 0.1000 0.1050 0.1050 0.1050 0.0900

0.2550 0.4600 0.2550 0.2300 0.2250 0.2450 0.2650 0.2300

0.3801 0.6857 0.3823 0.3448 0.3373 0.3694 0.3973 0.3448

0.0700 О O.O7OOO.O55OO.O5OOO.O65OO.O7OOO.O55O

Fig.11. Division of feature matrices in blocks

Then we calculate Dot Product of this first of blocks of the two Key matrices i.e. B1 and B'1 to obtain the Dotproduct_1 The threshold value, as mentioned before, for this Dotproduct_1 is: 1.3468 . For each of these values, if it is greater than the mean then we insert a ‘1’ at that position, otherwise it is a ‘0’. Hence we get the first set of binary key matrix as:

[ 1 1 0 0 0 1 0 0 ]

Finally, after computing all four sets of eight iterations i.e. a total of 32 iterations, we get the Final key matrix as:

1	1	0	0	0	1	0	0
0	1	0	0	1	1	1	0
1	1	0	1	0	0	0	1
0	0	1	1	1	1	1	1

Now, here is the result of CA encryption algorithm:

Enter the ECGhash code : 1 1 000 1 000100 1 1 1 01 101000100111111

The First block is: 1 1 0 0 0 1 0 0

The Ascii char for the 1 st block is: —

The Second Block is: 0 1 0 0 1 1 1 0

The Ascii char for the 2nd block is: N

The Third Block is: 1 1 0 1 0 0 0 1

The Ascii char forthe 3rd block is: :

The 41h block is: 0 0 111110

The Ascii char forthe 41hblock is: ?

The Biohashcode in ascii form is : —N=p? 00001111 11010000

0 0 1 1 0 0 1 1(4 rounds encryption of 1st block) 110 10 10 0 "

The ciphertext is: 11010100

First encrypted char in ascii is: 1= 10010001 01110010

10010101 (4 rounds encryption of 2nd block) 01111110 "

The ciphertext is: 01111110

2nd encrypted char in ascii is : ~

0011111 0(4 rounds encryption of 3rd block) 11000001

The ciphertext is: 11000001 3rd encrypted char in ascii is : -111000000 00000011

1 1 0 0 0 1 0 0(4 rounds encryption of 4th block) 00001111 "

The ciphertext is: 00001111

The clocktick is: 36.000000 4th encrypted char in ascii is: Д-

The encrypted ECGhashcode in ascii form: ^—4? The total output is: 1101010001111 1101100000100001111 cl=l 7.000000 (No of 1 in ciphertext block) c0=15.000000(No ofO in ciphertext block)

Y=14.000000(No of change of pattern of Is and 0s) Mean = 15.937500

Standard Deviation = 2.771202

Value of normal Variate Z = -0.699155

First block contains the plaintext and corresponding ASCII value. Then the plaintext block has been broken into 4 blocks plaintext and their ASCII value. After that the blocks has been converted to corresponding cipher text block using cellular automata rules. Then the 4 blocks of cipher text has been merged to the block of encrypted ECG hash code. In the reverse way we can get the plaintext block using the same cellular automata rule matrix.

Performance Analysis:

A. Analysis of the Algorithm:

There are 256 rules in 1D cellular automaton [14]. We have used only 2 rules. There are 2^8(256) combination of the 2 rules. We have used one combination. So the hacker need to test 256^8 combination which is impossible in case of brute force attack.

B. Statistical Analysis:

Statistical analysis is very much required in case of cryptographic algorithm to test the randomness of the cipher text. For this purpose runs test [18] has been performed to check the randomness of the algorithm. We have tested the following result for the data as following table:

Table 6. Runs Test Result

No. of Bits in Plaintext	Value of Z
32	-0.699155
64	1.016917
128	0.025013
256	-1.791818

From the above result it is observed that the value of the normal variant (z) is less than 1.96. Obtained value of Z in our study (|z| <1.96) implies that the difference between the observed and expected is not significant. Our hypothesis for random cipher text generation is true.

VI. Conclusion And Future Work

This work highlights a new aspect of verifying and validating an individual's identity to give him access privilege of sensitive and interesting information. Moreover, by applying an encryption algorithm over the generated ECG-hash code from ECG signal [21, 22], its degree of privacy preservation has increased. The essence of having two person's biometric feature has advantages over the other biometric traits that were used so far.

Current work gives more emphasize on offline ECG-hash code generation. The future extension of this work will be to make it an online one. Further, attempt will be to implement this system in a real time environment with some time constraints in number of attempts.

Список литературы Cellular Automata based Encrypted ECG-hash Code Generation: An Application in Inter human Biometric Authentication System

M. Dey, N. Dey, S. K. Mahata, S. Chakraborty, S. Acharjee and A. Das, “Electrocardiogram Feature based Inter-human Biometric Authentication System”, International Conference on Electronic Systems, Signal Processing and Computing Technologies, 2014.
S Latifi, N Solayappan, “A Survey of Unimodal Biometric Methods”, in International Conference on Security & Management, SAM, 2006, pp. 57-63.
S. S. Parvinder, I. Kaur, A. Verma, S. Jindal, S. Singh. (2009, Nov.). Biometric Methods and Implementation of Algorithms. International Journal of Electrical & Electronics Engineering [Online].3,(8),pp.3-8.
S. M. Rahal, H. A. Aboalsamah, K. N. Muteb, “Multimodal Biometric Authentication System – MBAS”, in 2nd IEEE Conference on Information and Communication Technologies, 2006, pp. 1026-1030.
M. I. Ahmad, W. L. Woo, S. S. Dlay, “Multimodal biometric fusion at feature level: Face and palm print”, in 7th International Symposium on Communication Systems Networks and Digital Signal Processing, 2010, pp. 801-805.
P. Lacharme, A. Plateaux. PIN-based cancelable biometrics, GREYC Research lab, Ensicaen - UCBN – CNRS [Online].3(2),. Available: http://www.ecole.ensicaen.fr/~lacharme/IJAIT2011.pdf. 2011, pp. 75-79
N. Radha1 and S. Karthikeyan, “An Evaluation of Fingerprint Security using Noninvertible Biohash”, International Journal of Network Security & Its Applications (IJNSA), 2011, Vol.3, No.4.
N. Dey, B. Nandi, M. Dey , D. Biswas, A. Das, S. S. Chaudhuri, “Generation of Bio Hash Code from Electrocardiogram Features”, in 3rd IEEE International Advance Computing Conference, 2013, pp. 724-728.
F. Maleki, A. Mohades, M. E. Shiri, A. Bijari, " A CA randomizers based on parallem CAs with balanced rules", International conference on Computational Science, ICCS, 2010, pp. 417-425.
L. Kotoulas, D. Tsarouchis, G. Ch. Sirakoulis, I. Andreadis, "1-d cellular automata for pseudo random number generation and its reconfigurable hardware implementation", Proceedings of IEEE international symposium on circuits and systems, 2006.
S. Roy, S. Nandi, J. Dasnasa, P. K. Pattnaik, "Application of cellular automata in symmetric key cryptography", Proceedings of IEEE International Conference on Communication and Signal Processing (ICCSP), 2014.
J. V. Neumann, Theory of Self Reproducing Automata, edited and completed by Burks, A.W. (Ed.), Univ. of Illinois press, London, 1966.
S. Wolfram, A new kind of science, Wolfram Media Inc., ISBN: 1-57955-008-8, 2002.
S. Nandi, B. K. Kar, Pabitra Pal Chaudhuri, “Theory and applications of cellular automata in cryptography”, IEEE Transactions on Computers, 1994, 43(12), pp. 1346-1356.
D. Mukhopadhyay, "Design and analysis of cellular automata based cryptographic algorithms", Doctoral thesis, Indian Institute of Technology, Kharagpur, 2007.
N. Dey, S. Mukhopadhyay, A. Das, S. S. Chaudhuri, “Analysis of P-QRS-T Components Modified by Blind Watermarking Technique Within the Electrocardiogram Signal for Authentication in Wireless Telecardiology Using DWT”, in IJIGSP, 2012, vol.4, no.7, pp.33-46.
N. Dey, S. Samanta, X-S Yang, A. Das, and S. S. Chaudhuri, “Optimisation of scaling factors in electrocardiogram signal watermarking using cuckoo search’, Int. J. Bio-Inspired Computation, 2013, Vol. 5, No. 5, pp.315–326
S. M. Ross, Introductory Statistics, Second edition, Academic Press, Elsevier, pp. 659-664.
N. Dey, A. B. Roy, A. Das and S. S. Chaudhuri, “Recent Trends in Computer Networks and Distributed Systems Security”, published in Springer Berlin / Heidelberg in Communications in Computer and Information Science, 2012, ISBN 978-3-642-34134-2, Volume 335, Part 2, Pages 347-357, DOI: 10.1007/978-3-642-34135-9_35.
N. Dey, S. Biswas , A. B. Roy, A. Das and S.S. Chaudhuri, “Analysis Of Photoplethysmographic Signals Modified by Reversible Watermarking Technique using Prediction-Error in Wireless Telecardiology”, International Conference of Intelligent Infrastructure, 47th Annual National Convention of CSI, 2012, McGraw-Hill Proceeding .
N. Dey, P. Das, A. Das and S.S. Chaudhuri, “DWT-DCT-SVD Based Blind Watermarking Technique of Gray Scale Image in Electrooculogram Signal”, International Conference on Intelligent Systems Design and Applications (ISDA-2012), pp. 680-685, 2012.
N. Dey, S. Biswas, P. Das, A. Das, and S. S. Chaudhuri, “Feature Analysis for the Reversible Watermarked Electrooculography Signal using Low Distortion Prediction-error Expansion”, 2012 International Conference on Communications, Devices and Intelligent Systems (CODIS), pp.624-627, 2012.

Еще

Статья научная

Cellular Automata based Encrypted ECG-hash Code Generation: An Application in Inter human Biometric Authentication System

Текст научной статьи Cellular Automata based Encrypted ECG-hash Code Generation: An Application in Inter human Biometric Authentication System

II. Motivation

III. Basic of Cellular Automata

V. Results

VI. Conclusion And Future Work

Список литературы Cellular Automata based Encrypted ECG-hash Code Generation: An Application in Inter human Biometric Authentication System