Цена как функция от зарплаты

В классической теории микроэкономики рассматривается многофакторная производственная функция Q = f ( x 1 ,x 2, ...x n ) , где Q -объем производства, x 1 ,x ₂, . x n - различные факторы производства, например: сырье, капитал, трудовые ресурсы, земля, помещения и т.д. Но как бы различны ни были факторы производства, у всех есть два общих свойства – они все являются продуктом труда человека или производной от него, и все измеряются в денежных единицах. Все ценности созданы человеческим трудом, а значит можно попробовать все факторы свести к одному фактору, а именно: к заработной плате Q = f ( x 3 ) , где x ₃ есть заработная плата.

Рассмотрим производственную цепочку, состоящую из конечного числа (n) предприятий (рис. 1). В результате деятельности предприятий цепочки на рынок поступает готовый продукт. У цепочки есть начало – предприятия первичной переработки (1.1, 1.2, 1.3), которые своими силами добывают или выращивают первичное сырье. Есть множество промежуточных стадий переработки (предприятия уровня 2 и 3). И, наконец, есть конечное предприятие цепочки (4.1), которое создает готовый продукт из полуфабрикатов, закупаемых у промежуточных предприятий.

Рис.1. Схема производственной цепочки, состоящей из предприятий, добывающих сырье, предприятий, перерабатывающих его, и предприятий, выпускающих готовый продукт и продающих его на рынке

Стрелки вниз означают путь движения денежных средств за оплату поставленной продукции, в обратную сторону идет поставка продукции. Вершина цепочки, предприятие 4.1, получает необходимые полуфабрикаты от предприя- тий второго уровня и продает готовую продукцию потребителю. Предприятия, добывающие первичное сырье (уровень 1), только отгружают свою продукцию и получают плату за нее. Все предприятия делают соответствующие платежи в бюджет (на рис. 1 не показано).

Количество проданного готового продукта, умноженное на цену продукта, есть выручка конечного предприятия и всей производственной цепочки. Эта выручка должна покрывать все издержки производства (стоимость сырья, комплектующих, коммунальные, налоговые и арендные платежи, заработную плату работников) и обеспечивать прибыль. Деньги, уплаченные покупателем, перераспределяются по всей цепочке в счет оплаты труда работников. Оплата за сырье, комплектующие, коммунальные услуги и налоги идут в оплату труда тем людям, которые их выполняют. Налоги идут на оплату труда чиновников или на выполнение социальных работ. Таким образом, вся цена товара есть стоимость труда людей, прямо (работники) или косвенно (бюджетники, чиновники) задействованных в его создании.

Рассмотрим более подробно процесс перераспределения поступившей выручки на конечное предприятие производственной цепочки. Часть этой выручки идет на зарплату сотрудников, на выплату приведенного подоходного налога ( α ) и налога на фонд оплаты труда ( β ). Кроме того, в цене продукта заложена прибыль предприятия ( γ ) и приведенный налог на прибыль ( δ ). Все это облагается налогом на добавленную стоимость ( ε ).

Выручка предприятия равна сумме следующих величин:

– чистой заработной платы – З_i ;

– приведенного подоходного налога – З_i * α , где α =14,9% – ставка приведенного подоходного налога (по величине равна подоходному налогу вычитаемой из «грязной» заработной пла-

Згр ты), а = Огр* —— , а гр - подоходный налог, 3

чист равный сегодня 13%, Згр – зарплата, начисляемая на предприятии (грязная), Зчист – зарплата за вычетом подоходного налога (чистая);

- налога на фонд оплаты труда ( 3 i + 3 i * а ) * * в , где в = 30% — ставка налога на фонд оплаты труда;

– чистой прибыли П_i ;

– налога на прибыль П *δ, где δ – приведен-i               Пг ная ставка налога на прибыль (5 = 5гр * —— , Пчист

П_гр – прибыль до налогообложения, П_чист – прибыль после уплаты налога, δ_гр = 20%);

– платежей за стоимость ресурсов С_i ;

– налога на добавленную стоимость к уплате, ε =18% – ставка налога на добавленную стоимость [1].

Прибыль предприятия составляет некоторую долю от чистой зарплаты. Долю для i -го предприятия обозначим γ_i .

П_i = З_i * γ_i ;

B_i = З_i + H_i + C_i .                             (1)

Оплата ресурсов для плательщика является расходом, а для получателя, соответственно, – выручкой . Тогда выражение (1) примет вид:

B = З + H + B ;

i i i          i — 1

H i = З д + ( 3 i + 3 i a}p + n i d + e ;

Bt = 3 i + 3 ia + (3 i + 3 ia в + П i +

+ П t d + B t - 1 + НДС ,

где:

i – номер предприятия в цепочке передела;

B_i – выручка i -ого предприятия;

H_i – налоги;

П_i – прибыль;

C_i – платежи за ресурсы.

Выразим прибыль и налог на прибыль через заработную плату:

B i = ³i ⁺ З а ⁺ ( ³i ⁺ З а ^{) e + 3}i Y i ^{+ 3}i Y i B ⁺ B i - i ⁺ + НДС ;

НДС = (3i + 3i a + (3i + За в + 3iYi + 3^5) * 8;

B i = [ 3 i ( 1 + a ) + 3 i ( 1 + a >  + 3 i Y i + 3 Yd ]( 1 + 8 ) +

⁺ B i - 1 ^;

Bi = 3i[(1 + a )(1+ P) + Yi + Yid K1+ e ) + Bi-1 =

= 3 i [ ( 1 + a )( 1 + P) + Y i (1 + d ) ] ( 1 + 8 ) + B - 1 . ₍₄₎

Аналогично действуя для i -1 предприятия, получаем рекуррентную формулу выручки:

B i - 1 = 3 i [( 1 + a X1 + в ) + Y i - 1 (1 + ^ )X1 + _E ) + B i - , ;

B 2 = З ₂ [( 1 + a )( 1 + в ) + Y 2 (1 + » ) ]( 1 + e ) + B i ; (6) B , = 3 , [( 1 + a )( 1 + в ) + / , (1 + 5 ) ]( 1 + s ) .      (7)

Выручка первого в цепочке предприятия состоит только из заработной платы, прибыли и на- логов. Оно является монопольным (не зависящим от других поставщиков) производителем своего продукта или услуги.

В свою очередь, последнее предприятие в цепочке переделов поставляет готовую продукцию конечному потребителю.

Подставляя значение В ₁ из (7) в (6), далее полученное значение В ₂ в выражение для получения значения В ₃ и так далее до n -ого, получим:

B n = З п [ ( 1 + а Х1 + в ) + Y i (1 + 8 ) ] ( 1 + 8 ) + З п _ч[( 1 + а )( 1 + в ) + + Y i (1 + 8 ) ] ( 1 + 8 ) ⁺ "' ^{+ 3} 2 ^{[( 1 + а )( 1 + в ) + Y} i ^{(1 + 8 ) ]( 1 + 8 ) +} + 3 1 [ ( 1 + а )( 1 + в ) + y (1 + 8 ) ] ( 1 + 8 ) .                      ⁽⁸⁾

Если в цепочке k переделов и в каждом переделе участвует до n предприятий, то kn

B ki £2 3 ki [ ( 1 + « X¹ + в ) + Y i (1 + 8 ) ] ( 1 + £ ) .

1 i = i                                                        (9)

С учетом действующих налоговых ставок получим _{k n}

B . ^ Z З ( 1’762 + 1,416 ^ i ) . 1      i = 1

Если только часть продукции i -го предприятия задействована в конкретной цепочке (предприятие может быть задействовано и в других цепочках), то высчитывается доля выручки реализации этой продукции в общей выручке данного предприятия ( λ ), и уравнение (9) принимает окончательный вид kn

B ki = Z Z ^X ki 3 ki [( 1 + a X1 + в ) + Y , (1 + » ) ]( 1 + e ) 1       i = 1

Найдем величину всех налогов i -ого предприятия, выраженных через заработную плату. Из (2)

Н, = 3 i « + ( 3 i + 3 a p + П 5 + НДС =

= 3 i ( a + ( 1 + а ) p + У5 ) + ( 3 i + 3 i a + ( 3 i + 3 i a в + + 3 i y i + 3_i y _i 5' ) * s = 3 i ( a + ( 1 + a ) p + y i 5 +

+ ( 1 + a ) (1 + в ) * s + У i s + Y i 5s =

= 3 i ( a + ( 1 + a ) (( P + (1 + в )* s ) + y i *

*( 5 i + s (1 + 5 )) .

H ₍ = 3 i ( a + ( 1 + a ) (( p + (1 + в )* e ) +

+ У1*(5,+ e(1 + 5)).

Сумма налогов в конечной выручке (из n переделов) будет равна

H ki =lL 2 3 -^u' + (! + ^a X d + (1 + в )* £ ) +

+ V/a>. + £(1 + 5)).(12)

С учетом участия предприятия в других цепочках

H •    L IL ^A ki 3 ki ( ^{a +} ( 1 ^{+ a} Х в + (1 + в )* £ ) +

+ Yi*(5i+ £(1 + 5)).(13)

Величина налога на добавленную стоимость рассчитывается по формуле:

Н н^дс = з. ( ( 1 + a ) (1 + в )* £ + Y i £ (1 + ⁸ )) =

= З . £ ( ( 1 + a ) (1 + в )* £ + Y i (1 + 8 )) .

Суммарный НДС в выручке будет равен нkiДС =:L Z Зк,= ((1 + aX1 + в- = + 1 i=1

+ / , (1 + 8 )).

С учетом коэффициента нkДС = Z :Ё W(! + aX1 + PV = + 1 i=1

+ Y i (1 + 8 )) .

Остальные налоги (без НДС) составят ((10)– (12)).

Н б^езНДС = X i 3 i ( a + ( 1 + a ^^P + Y i ^ ) .        (17)

Сумма налогов в конечной выручке (из n переделов) без НДС будет kn

Н б, НДС ₌ £ ^ _A ki 3 _ti ( _{a + ( 1} + a k₎ p + Y i ^ ) .

1 i = 1

Найдем зависимость цены от зарплаты.

B _ki = Ц _ki * M _ki , где Ц_ki – цена товара, М_ki – количество товара. Предполагается, что количество сырья равно количеству товара, из него сделанного, потерь (усушки, утряски, усадки и т.д.) нет. Реально потери существуют, и одна из задач – это снижение потерь при производстве и переработке сырья.

kn

B ki = ^ z 8 ki [ ( 1 + a )( 1 + p ) + Y i (1 + 5 ) ] ( 1 + s ) =

• 1    i = 1

= Ц ki* M ki ;                                   (19)

]T ^h З к. Кх + a X1 + e ) + Y i (1 + 5 ) ] ( 1 + e )

Ц к =                                   (20)

Конкурентоспособность по цене - важней шая составляющая успеха предприятия на рынке. Рыночная цена определяется внешними факторами - спросом и предложением. Если пред приятие не монополист, влиять на рыночную цену невозможно. Задача предприятия - себестоимость продукта должна быть меньше рыночной цены продукта или равна ей. Иначе предприятие убыточно.

Рассмотрим простой случай, когда прибыль предприятий производственной цепочки равна нулю - Y i = 0 и доля участия предприятий максимальна X i = 1 . Очевидно, что когда X i = 0, это означает, что i -ое предприятие не участвует в данной производственной цепочке. Пусть чистый фонд оплаты труда на всех предприятиях одинаков и равен З₀.

kn

^ £ З ^ + а )( 1 + в ) + Y i (1 + <1 + е )

1 i = 1

Ц ki =

M ki kn

S S з»

* 1      I = 1

Mki

) n З- .

Mki

= ( 1 + а )( 1 + в )( 1 + е )’ = ( 1 + а )( 1 + в )( 1 + е )

Из (21) видно, что цена продукта прямо пропорциональна величине налоговой нагрузки, суммарной чистой заработной плате сотрудников участвующих предприятий и обратно пропорциональна количеству произведенного продукта.

Чем меньше фискальная нагрузка на предприятия, тем предприятия имеют больший запас по цене. Чем более высокотехнологично производство, тем меньше требуется переделов, что, в свою очередь, повышает конкурентоспособность по цене. Кроме того, высокотехнологичное предприятие может легко, без лишних затрат, увеличить количество выпускаемого продукта, что, в свою очередь, понижает цену единичного товара и увеличивает конкурентоспособность на рынке. Чем больше увеличивается объем производства, тем больше увеличиваются объемы закупки сырья и комплектующих, что приводит к снижению оптовой цены. Но, с другой стороны, растут и затраты на оплату труда. Предприятию необходимо нанимать дополнительных работников или поднимать производительность труда. Если приобретается высокопроизводительное оборудование, его обслуживание требует высококвалифицированных специалистов, а они стоят дорого.

Цена продукта определяется рынком. Из (21) следует, что при фиксированной цене и налоговой нагрузке мы можем определить суммарную зарплату участников всех конкурирующих цепочек:

Мм * Ц м

( 1 + а )( 1 + в )( 1 + е )

kn

= Z Z З ¹

1 i = 1

= ³ 0 n .

Сравнивая с аналогичной величиной других цепочек, можно легко определить конкурентоспособность продукта. Чем ниже суммарная чистая зарплата цепочки, тем ниже цена продукта, и наоборот.

Рассмотрим, как меняются зависимости затрат на ресурсы от объема приобретаемых ресурсов.

Пусть цена закупаемого сырья зависит от объема следующим образом [2; 3]: ц = ц ₀ - kx, где ц - конечная цена приобретенного сырья;

ц ₀ - начальная цена сырья;

к - коэффициент уменьшения цены в зависимости от объема закупки;

x - объем закупки.

Для 0 <  x <  x опт mix , ц = ц ₀ - диапазон розничных цен. До определенных объемов закупок цена не уменьшается (рис. 2).

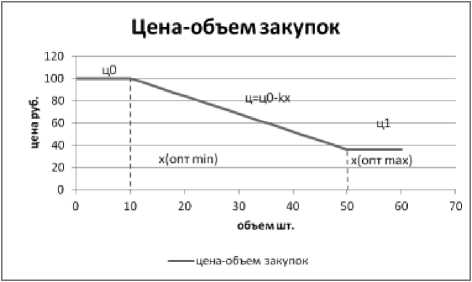
Рис. 2. График зависимости цены от объема закупок

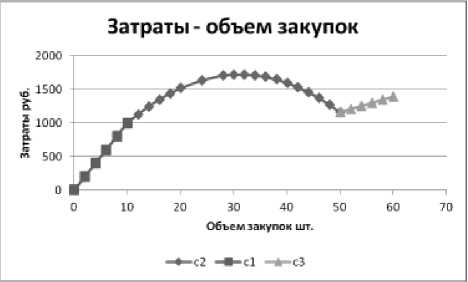
Рис. 3. Зависимость затрат от объема закупок

Для x ^{опт mix} ≤ x ≤ x ^{опт max} – диапазон снижающихся оптовых цен. В этом диапазоне объемов закупок оптовые цены падают.

Для x > x ^{опт max} , ц = ц ₁ – диапазон постоянных оптовых цен. То есть, начиная с некоторого количества закупаемого сырья цена перестает падать и уже не зависит от объема.

Затраты на закупку сырья вычисляются следующим образом.

Для 0 ≤ x ≤ x ^{опт mix} , ц = ц ₀, С ₁( х ) = ц * х = ц ₀ х . Это прямая линия, проходящая в начале координат.

Для x ^{опт mix} ≤ x ≤ x ^{опт max} , С ₂( х ) = ц * х = ц ₀ х – – kх ².

Это и есть формула параболы с выпуклой вверх

_ 2

вершиной в точке x = —, равной з ( x ) = -0- и пе-

• 2    к                2 к

ресекающей ось абсцисс в точках х = 0 и x = ^{ц 0} .

k

Для х > х ^{опт max} , ц = ц ₁. С ₃( х ) = ц * х = ц ₁ х. Это прямая линия, проходящая через начало координат.

Платежи одного предприятия на приобретение сырья являются его расходами, а для предприятия – получателя этих платежей – доходами. Преобразуем (1) в вид:

B i = З п + B i - 1 ;

З п = З + H .

Налоги состоят из подоходного налога, который исчисляется от чистой заработной платы, налог на фонд оплаты труда – налогом на прибыль и налогом на добавленную стоимость.

B i = З п i + B i 1 - э ти платежи при поступлении на предприятия являются выручкой и соответственно делятся на зарплату и иные платежи. И так далее:

B i = З п + B i ;

в₃ = з п₃ + в 2 ;

B 2 = З П 2 + B ;

B ₁ = З п ₁ .

Общая формула такова:

i - 1

Bi = Зп + Bi -1 = ЗDi + ^ Зц. -1, где i – номер предприятия в цепочке передела;

Bi– выручка i-ого предприятия, учитывая, что Cz = Bt -, , Bki = Зпfc + Cki.

Здесь C_ki – стоимость сырья или иного закупаемого на стороне ресурса i -ым предприятием.

ki

C ki = ∑ ∑ З п k i - 1 .

Сумма начинается с 2, так как первое предприятие никому не платит за сырье, оно само его добывает. Так как затраты есть суть зарплата, то конкурентоспособна та экономика, в которой уровень зарплат ниже.

На диапазонах, где цена на сырье не зависит от объема закупок (закупается слишком мало или слишком много), его затраты растут линейно.

Начиная с некоторого объема переработки зарплата (рис. 4) перестает расти. Владельцы бизнеса получают больший объем продукта без дополнительных затрат на его переработку. В этом случае затраты владельцев представляют собой только стоимость самого ресурса. Таким образом, появляется резерв для снижения цены при больших объемах продаж. Оптовая цена падает за счет снижения владельцами бизнеса своей доли прибыли в цене. До некоторого объема переработки сырья работники работают на себя, налоги, ресурсы, а дальше работают на владельцев (зарплата сотрудников не растет).

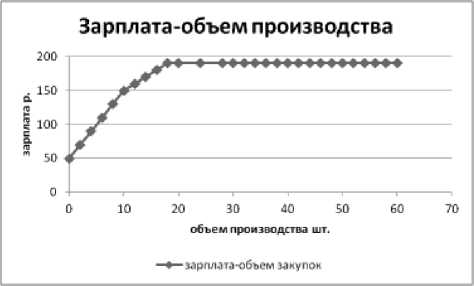
Рис. 4. График зависимости зарплаты от объема производства

Таким образом, уровень налоговой нагрузки и уровень средней зарплаты играют ключевую роль в формировании цены на продукт. Чем ниже налоговая нагрузка и уровень оплаты труда, тем ниже цена продукта и тем он конкурентоспособней на рынке. Необходимо работать в конце диапазона снижающихся оптовых цен, где затраты на приобретение сырья сокращаются максимально и отсутствуют дополнительные затраты на заработную плату. Для повышения конкурентоспособности продукции необходимо снизить цену. Это возможно только при снижении государством налоговой нагрузки на предприятия и физических лиц.