Ценологическое моделирование электропотребления предприятий АПК

Система электроснабжения современного предприятия агропромышленного комплекса (АПК) образована практически бесконечным числом элементов. В число этих элементов входит как низковольтная аппаратура, так и силовые трансформаторы. Это комплексное электрическое хозяйство является системой нового типа, где свойства системы не вытекают из простого сложения свойств ее отдельных элементов. Для анализа электропотребления действующих предприятий АПК недостаточно изучать и описывать только тот или иной элемент или электрическую цепь, где связи функционально определены, необходимо описать все множество элементов в целом.

По мере роста и усложнения сельхозперера-батывающих предприятий актуальными становятся проблемы их построения и обеспечения функционирования. Законы развития техники, включающей отдельные элементы, и живой природы, состоящей из отдельных особей, имеют много общего. Поэтому представляется возможным описывать сложные электротехнические системы предприятий АПК на основе понятий и законов биологии. Подобные системы рассматриваются в науке как ценозы (биогеоценозы, социоценозы, бизнес-ценозы и т.д.).

Известно, что в 1877 г. при исследовании свойств отдельных особей и совокупностей живых организмов Клаус Фердинанд Мебиус ввел понятие «биоценоз». Биоценоз - совокупность живых организмов, обитающих на определенном участке, где условия внешней среды определяют его видовой состав.

Термин «техноценоз» и ценологический подход предложены в 1974 г. Б.И. Кудриным, который определяет техноценоз как сообщество всех изделий, включающее все популяции; ограниченное в пространстве и времени, имеющее слабые связи и слабые взаимодействия элементов (изделий), образующих систему искусственного происхождения, которая характеризуется несопоставимостью времени жизни ценоза и особи, невозможностью выделения однозначной системы показателей. Устойчивость технической системы обусловлена действием законов энергетического и информационного отборов по аналогии с живыми системами, где действует закон естественного отбора [1,2].

Отличительным признаком любого техноценоза является тот факт, что всю документацию на этот ценоз собрать нельзя принципиально. Построение техноценозов определяется законами техноэволюции, а структура его образующих элементов по повторяемости видов устойчива и определяется гиперболическим Н-распределением [1].

Структура ценозов описывается разными типами распределений:

• •    видовое распределение - зависимость числа видов с равным количеством особей от количества особей в виде;

• •    ранго-видовое распределение - ранговое представление основывается на расположении элементов в порядке убывания величины описывающего их параметра или частоты появления;

• •    ранговое распределение по параметру, при расположении видов в порядке уменьшения какого-либо параметра.

Кудрин Б.И. предложил использовать модель Н-распределения для математического описания видового и рангового распределения

• ¹    уя+^а

где Л, - теоретическое значение числа видов для всех г, X,- численность популяции i, A, a - постоянные видового распределения.

В электроэнергетике, как правило, аналогично определяют электропотребление:

W = г В ’ где Жг - электропотребление особи с рангом г, ^ - электропотребление особи с рангом г = 1 (максимальное электропотребление); Р - ранговый коэффициент, характеризующий форму кривой распределения.

Отмеченные ценологические свойства систем электроснабжения предприятий констатируют устойчивость явления, проявляющегося с определенного уровня организации некоторого множества элементов с неопределенными связями: способность ценозов формировать в процессе образования и сохранять в процессе развития устойчивую структуру при наличии различных механизмов отбора.

В работе [3] предполагается, что оптимальным является такой техноценоз, который по своим функциональным показателям характеризуется максимальной энтропией и обеспечивает выполнение поставленных задач, т.е. идеальное выполнение своего функционального назначения. Дан- ная теория предполагает существование некоторого идеального распределения элементов ценоза, причем стабильность системы характеризуется значением рангового коэффициента р, находящегося в пределах от 0,5 до 1,5. Функциональное выполнение своего назначения и понятие «идеальная техническая система» уже нашли свое применение в электроэнергетике [4].

Объясним существование идеальной технической системы с точки зрения гармонии. Будем считать, что гармония и идеальное распределение ценоза как системы, выполняющей свое функциональное назначение, подчиняются «Золотому сечению», а понятие «Золотое сечение» неразрывно связано с числами Фибоначчи. Числовой ряд, носящий сегодня его имя, вырос из задачи с кроликами, которую Фибоначчи изложил в своей книге «Liber abacci», написанной в 1202 году. В науке понятие «Золотое сечение» определяет такое деление отрезка на две части, при котором длина отрезка так относится к большей части, как большая часть относится к меньшей [5].

Движение естествознания к пониманию и описанию таких явлений, как самоорганизация и гармония требует нового математического аппарата. В отличие от классической математики с доминированием фундаментальных математических констант ^ и е, в математике живой природы доминирует константа «Золотого сечения» -Ф = 1^ = 1,618.

Покажем значение «Золотого сечения» в сфере организации электротехнических систем по аналогии с живой природой. Если взять убывающий числовой ряд 1,0; 0,62; 0,38; 0,24; 0,15; 0,09 и т.д. (что практически соответствует шкале мощностей трансформаторов), состоящий из чисел с коэффициентом 1/1,618 , и построить кривую (рис. 1), проходящую через этот ряд чисел, то можно подобрать функцию, описывающую эту кривую:

Ф, = 1,663 е “°-489 г.

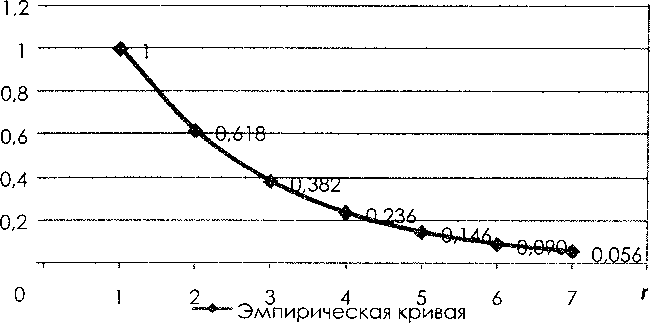
Рис. 1. Ряд чисел и аппроксимирующая кривая

Проведем некоторые преобразования данной формулы. Заменим с приемлемой точностью число 1,663 отношением 5/3 (отношение двух соседних членов ряда Фибоначчи), что в свою очередь приблизительно равно Ф. Число е заменим на число Ф2, показатель степени -0,489г заменим на - г/2. После преобразования получим следующее выражение:

фi = фф2^~г/2} = ф0~г) = 1/ ф(г-0

Эта функция, по нашему мнению, является идеальной кривой, описывающей соотношение количества особей и видов в техноценозе.

Каждое предприятие находится в динамическом процессе создания, существования, трансформации и ликвидации. Подобные этапы сопоставимы с этапами жизни биологических объектов. Таким образом, разнообразие видов и диапазон разброса параметров предприятий - особей в ценозах всегда настолько велик, что это делает невозможным применение привычной для нас классической математической статистики. Отсюда возникает потребность оперировать выборкой параметров в целом. Для этого необходимо построить ранговое распределение особей техноценоза.

Наиболее эффективным и к настоящему времени апробированным инструментом ценологических исследований является ранговый анализ -метод исследования больших систем, имеющий целью их статистическое описание, а также оптимизацию и полагающий в качестве основного критерия форму видовых и ранговых распределений. Исходной посылкой негауссовой математической статистики является признание существования таких объектов (ценозов), в которых выборки параметров, описывающих отдельные элементы, не имеют математического ожидания, а дисперсия равна бесконечности [1].

Под ранговым распределением понимается убывающая последовательность значений параметров, упорядоченная таким образом, что каждое последующее число меньше предыдущего, и поставленная в соответствие рангу (номеру по порядку, ряду натуральных чисел, расположенных в порядке возрастания).

Практическая реализация анализа техноценозов эффективно осуществляется в рамках процедур рангового анализа, который включает следующие этапы:

• 1.    Выделение техноценоза.

• 2.    Определение перечня видов в техноценозе.

• 3.    Задание видообразующих параметров.

• 4.    Параметрическое описание техноценоза.

• 5.    Построение табулированного   рангового

• 6.    Построение графических     ранговых

• 7.    Аппроксимация распределений.

распределения.

параметрических распределений.

Рассмотрим возможность применения ценологического моделирования электропотребления на примере предприятий АПК. В качестве параметра исследования выберем фактическое электропотребление хлебоприемного предприятия Красноярского края. При расчете воспользуемся данными электропотребления по «Гляденскому ХПП» за 2004-2008 гг. Динамика фактического электропотребления «Гляденского ХПП» за 2004 г. по месяцам представлена на рис. 2.

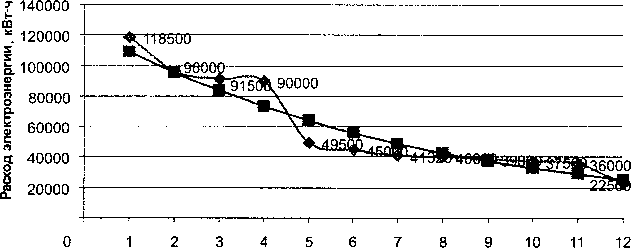
Проранжируем фактическое электропотребление по степени убывания следующим образом: первому рангу г=1 соответствует максимальное электропотребление (118 500 кВт-ч), второму рангу г=2 соответствует следующее по величине значение электропотребления (96 000 кВт-ч) и т.д. Последнему рангу г=12 соответствует минимальное значение потребляемой электроэнергии (22 500 кВт-ч).

Проведем аналогичную процедуру ранжирования для следующих временных периодов, результаты которой представлены на рис. 3.

Как видим из диаграмм, ранжированные объ-

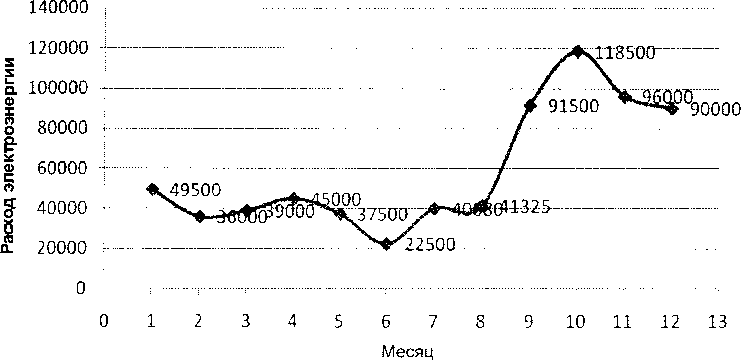
Рис. 2. Электропотребление Гляденского ХПП за 2004 г.

■ 2004 год ш 2005 год ■ 2006 год ■ 2007 год ■ 2008 год

Рис. 3. Ранговое распределение электропотребления за 2004-2008 гг.

Таблица 1

Сводная таблица по расчетам

Xi	У,	X, xlny,	X,2	lnyz	У^
1	118 500	11,682	1	11,68	108 920,80
2	96 000	22,944	4	11,47	95 286,85
3	91 500	34,272	9	11,42	83 359,50
4	90 000	45,630	16	11,40	72 925,14
5	49 500	54,048	25	10,80	63 796,88
6	45 000	64,286	36	10,71	55 811,23
7	41 325	74,404	49	10,62	48 825,17
8	40 080	84,789	64	10,59	42 713,57
9	39 000	95,141	81	10,57	37 366,98
10	37 500	105,32	100	10,53	32 689,64
и	36 000	115,40	121	10,49	28 597,78
12	22 500	120,25	144	10,02	25 018,11
	706 905	828,18	650	130,35	695 311,71

Таблица 2

Год	A	A У~ Bx
2004	61,48	13,59
2005	67,6	6,39
2006	66,54	5,5
2007	68,31	6,95
2008	67,06	10,95

Yuzhannikova Alexandr Yurievich. Candidate of technical sciences, professor of the Electrotechnical Complexes and Systems department of Siberian Federal University, Krasnoyarsk. Professional interests - optimization of electrical power consumption and preservation at industrial enterprises. Contact telephone: 007 9029 403085.

емы электропотребления на протяжении пяти лет сохраняют характер изменения, для аппроксимации которого примем формулу

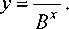
в которой символом * помечены натуральные логарифмы соответствующих переменных. По результатам решения получены следующие значения А и В:

А* = 11,7321; В* = 0,133729;

Значение эмпирической ранжированной функции энергопотребления обозначим через у,. а

А = е^А = 124504,8562; S = e⁵* =1,14308.

ранги через xz.

Коэффициенты А и В найдем методом наименьших квадратов. Исходная выборка для 2004 г. и сопутствующие данные по расчетам представим в сводной табл. 1.

Задача сводится к решению следующей системы уравнений:

Графики исходной и аппроксимируемой функции показаны на рис. 4.

Оценим точность метода по средней погреш

ности

д- ¹ У ^"X^)

12 Й У,

для двух аппроксими

/ И

-ПА А В- £

=-f>x

рующих функций электропотребления по «Гля-денскому ХПП» и результаты приведем в табл. 2.

Таким образом, предложенная методика ценологического моделирования электропотребления предприятий АПК на основе рангового анализа позволяет повысить качество прогнозирования электропотребления.

Ранг

—Ф— ранжированный ряд             —®— аппроксимирующая кривая

Рис. 4. Аппроксимирующая кривая и ранжированный ряд

Погрешность аппроксимации, %