Centralized adaptive algorithm for the procedure of optimal conditional search for the place of failure of dynamic systems

Programs of the Ministry of Defense of the Russian Federation aimed at improving the quality of control of TS of weapons and military (special) equipment are used to maintain and restore the serviceable (opera- ble) state of various types of systems. At the same time, the analysis of the properties of systems of the form [1; 2], the results of scientific research of the theory, methods and means of determining TS systems [3; 4] have shown that the complexity of systems has reached a level at which, in most cases, an individual human expert or a group of experts is not able to fully and accurately process the amount of information about inhomogeneous processes occurring during the operation, damage and system failures. Consequently, the further development of TD as a necessary component of the control process of TS systems seems to expand the base of theoretical foundations and their practical applications, focused on the partial or complete transfer of analytical functions of an expert from a human operator to a machine.

An important role in this is assigned to the improvement of algorithms that provide maximum automation of optimal operations to find the place of failure of systems.

Algorithms for probabilistic modelling of problems of combinational and sequential recognition of system failures are developed in great detail and are considered in special literature, for example [5; 6]. We also note a useful overview of current results in the subject area. So, in articles [7; 8] algorithms for identifying defects and assessing their impact on the safety of systems operation using the rules of inference and formal conceptual analysis are proposed; in [9], the algorithms for TD of the compressors of aircraft gas turbine engines were developed using parameters that are highly sensitive to changes in the vehicle of the controlled object; in the work [10], original algorithms for individual and group diagnostics of the functioning of information-measuring complexes for electricity metering are presented; publication [11] argues the possibilities of applying the achievements of neural network technologies in the algorithms of TD of digital systems.

Taking into account the actualization of the vehicle control strategy based on the state and the mixed vehicle control strategy, as well as the processes of increasing the readiness coefficient of military systems, [2] as the most natural, practically feasible form that meets modern requirements, we will determine the feasibility of further improving the failure recognition procedure the development of an algorithm that has the properties of centralization and adaptation. The block "decision making" of such an algorithm is considered as the central one, which provides the functions of the regulator when the proposed algorithm is applied for its intended purpose. The adaptation property reflects the fact that the formation of branches of such an algorithm is carried out on the basis of possible structures of systems, and the connections between the branches of the procedure for conditional search for the place of failure of systems are implemented on the basis of an optimal combination of all algorithmic blocks.

Presentation of the initial data and the main result

In the implementation of the structure and content of the algorithm, the apparatus of the theory of pattern recognition is used and the tools of direct probabilistic (imitation) modelling are used, in which the algorithm reproduces, imitates real human actions that are randomly dependent from the type of a priori information and the structure of the system.

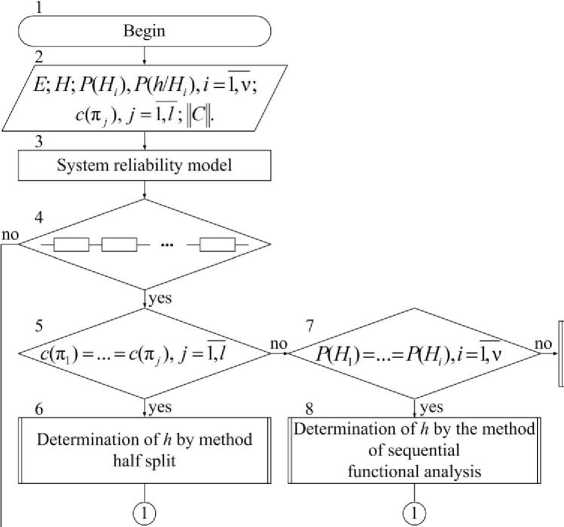
Based on the classical formulations of the problem of optimal search for the place of failure of systems [12], the synthesized algorithm is presented in the form of a block diagram of operators, separate of which represent a fairly large group of elementary arithmetic and logical operations, as shown in fig. 1.

The developed algorithm operates on the basis of the initial data systematized in operator 2.

The system under study, which belongs to the class of dynamical systems, is represented in the so-called system theory by the "input - state - output" model [12–14].

Ε = ( T , X , Y , Z , A , F ), (1)

where T is a set of points in time t; X is a set of input signals of the system x; Y is the set of output signals of the system y; Z is the set of state variables of the system z; A – operator of outputs, describing the mechanism of the formation of the output signal as a reaction of the system to internal and external disturbances; F – is the transition operator, reflecting the change in the state of the system under the influence of internal and external disturbances.

Determination of h by method linear programming

Риc. 1. Блок-схема оптимального условного алгоритма поиска места отказа динамических систем (Начало)

Fig. 1. Block diagram of the optimal conditional algorithm for finding the place of failure of dynamic systems (Beginning)

Риc. 1. Продолжение (начало на с. 277)

Fig. 1. Continued (beginning on р. 277)

To organize the recognition of failures, it is necessary to use a pre-formed DS reference dictionary, the number of descriptions in which should be equal to a given number ν of the determined i -th classes of the TS of the system, i = 1,ν . The DS system dictionary, formed in a form convenient for further actions, is presented in the form of vectors

H i = ( h i 1 , h i 2 , …, h ij , …, h il ), i = 1,ν, (2)

whose components are the supporting j -th (out of the total number l ) DS h i 1 , …, h il of any type describing properties of the system of this class TS H i , i = 1,ν .

It is known that the j -th DS h ij , j = 1, l means a possible outcome of an elementary check in the i -th class of TS of the system and shows what the outcome of an elementary check should be if the state of the system belongs to the i -th class of TS [12]. Therefore, to denote an elementary check, the symbol π is used with the index j – π j , j = 1, l , of the same name for the number of DSs, and for brevity, an elementary check is hereinafter called simply a check.

Риc. 1. Окончание (начало на с. 277)

Fig. 1. End (beginning on р. 277)

It should be noted here that the descriptions of classes formed at the stage of preliminary study of the properties of systems do not remain unchanged. They are usually refined according to the results of recognition of newly created or modernized systems, which determines the open architecture of the algorithm.

The set of specified classes, obtained at the end of the learning process, forms an array of the alphabet of classes of the TS system in a mathematical formulation, similar to formula (2), but representing it in a form that excludes programming errors

	h 11 h 21	h 12   ... h 22   ...	h 1 j h 2 j	...     h 1 l ... h 2 l
H =	... hi 1 Ill	...      ... h i 2... 111      111	... hij 1 1 1	...      ... ...     hil 111      111
	... h χ1	...      ... h χ2   ...	... h χ j	...      ... ...    h χ l
	... h ν1	...      ... h ν2   ...	... h ν j	...      ... ...    h ν l

The alphabet of classes (3) assumes the existence of a maximum number of separate classes corresponding to inoperable states of the system. It is also assumed that the recognition of failures is performed on the set of the indicated DSs and that their number is sufficient for the correct classification of all inoperable states of the system.

By their nature, all states of systems are random events caused by the randomness of failures of individual elements and other random factors. Under these conditions, generally speaking, it is necessary to consider the TD problem in a probabilistic formulation, and its solution within the framework of the application of probabilistic decision-making methods, assuming the presence of information specifying:

• – the probabilities of the i -th classes of the TS of the system P ( H i ), i = 1,ν ;

• -    the probabilities of the appearance of images of the system h when the system is in the i -th classes of the TS P ( h / H i ); i = 1^ ;

• -    the prices of the j -th checks c (n j ), j = 1, l .

In addition, in the structure of the initial data generated in operator 2, it is mandatory to provide for the presence of a payment matrix that assigns average losses in case of correct and erroneous decisions of technical diagnostics obtained at the stage of training the system с11,   с12,   ..., с1ν

II c|| = cν1,

c ν2,    ...,    c νν

On the main diagonal of the payoff matrix (4), there are losses with correct decisions, on the right side of the main diagonal are losses associated with errors of the 1st kind, on the left are losses associated with errors of the 2nd kind [15].

Upon completion of the process of entering the initial data, using operator 3, an analysis of the interaction of elements with each other in the spatio-temporal organization of the system that determines the types, nature of connections and relationships between elements is performed. Operator 3 is typical for identifying a sequential model of system reliability or other structure of connecting elements and is intended to determine the conditions for the applicability of one of the known methods for finding the place of system failure. To structure the system, frames can be used - constructions for describing a certain system, that has certain properties and stores all information about the properties and relationships of the system [4].

In general, such an analysis is an intermediate stage in solving the TD problem on a computing machine.

Next, a group of operators 4-16 functions, designed to reproduce the failure recognition method and determine the system image, which, by analogy with the DS dictionary (2), is represented in the form of vectors h = (h 1, h2, .... hj, ., hl).                                              (5)

where h 1 , .., h l are features of any kind obtained as a result of performing checks n j , j = 1, l .

Obviously, features h j , i = 1, v , j = 1, l from the DS dictionary of system (2) and features h j , j = 1, l from the image of system (5) assume comparable units and an identical form that allows their comparison.

Logical operator 4 provides a branching of the general procedure for recognizing failure depending on the identification of the structure of the system.

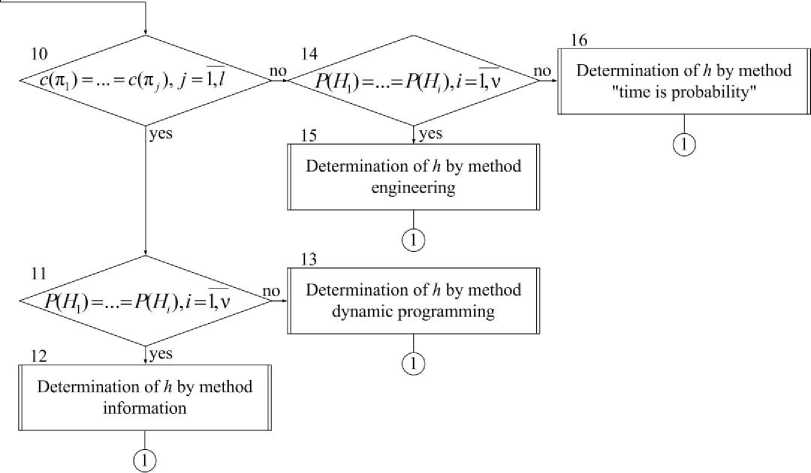
When sequentially connecting elements in the system, operator 5 checks the condition of equality of prices of the checks performed. When the condition c ( П 1 ) = c ( П 2 ) =.= c ( n j ) is satisfied, the set of checks P = { П 1 , П 2 , . n j }, j = 1, l is obtained, and the final image formation of the system h of the form (5) is carried out using the program of the half-partition method [ 6] introduced by operator 6. Here we note that the conditions for the applicability of the half-partition method are not limited by the requirements for the equality of the probabilities of the classes of TS of the system P ( H i ), i = 1, v .

If the condition c(П1) = c(Л2) =.= c(nj), j = 1, l is not satisfied, then operator 7, regardless of the previous cycle checks the equality of the probabilities of the classes of the TS of the system, P(H1) = P(H2)=.=P(Hi), i = 1, v and connects operator 8, which implements the program of the method of sequential functional analysis [5]. Failure to meet the conditions c(П1) = c(Л2) =.= c(nj), j = 1,l and P(H1) = P(H2) = .= P(Hi), i = 1, v , means the choice of a failure recognition program by the linear programming method [12] contained in statement 9.With a mixed structure of connecting elements in the system, control from operator 4 is trans- ferred directly to operator 10, which, when the prices of the performed checks, c(π1) = c(π2) =…= c(πj), j= 1,l, are equal, requests operator 11. If probabilities of classes of TS of the system, P(H1) = P(H2) = …= P(Hi), i = 1,ν , obtaining a set of checks P = { π1, π2, … πj }, j= 1,l, and the final formation of the image of the system h of the form (5) is carried out using the information method program [6].

The lack of conditions for the applicability of the information method leads to the need to include in the operation of the algorithm operator 13, synthesizing the method of dynamic programming of recognition of failures [6].

If the condition c ( π 1 ) == c ( π 2 ) =…= c ( π j ), j = 1, l does not hold for a mixed structure of the connection of elements in the system, then operator 14 checks the equality of the probabilities of the classes of the TS of the system, P ( H 1 ) = P ( H 2 ) = …= P ( H i ), i = 1,ν , and connects operator 15, which implements the program of the "engineering" method of finding the place of failure of the system [5]. If the prices of checks are not equal, c ( π 1 ) ≠ c ( π 2 ) =…≠ c ( π j ), j = 1, l , and the probabilities of the classes of the TS of the system are not the same, P ( H 1 ) ≠ P ( H 2 ) ≠ …≠ P ( H i ), i = 1,ν , then to establish the set of checks P = { π 1 , π 2 , … π j }, j = 1, l and to determine the image of the system h of the form (5), the "time - probability" method [5] is selected, contained in operator 16.

Thus, the operation of the group of operators 4–16 is carried out under the conditions of an active experiment, which dictates the need to form certain optimality requirements for specific control conditions of the TS systems.

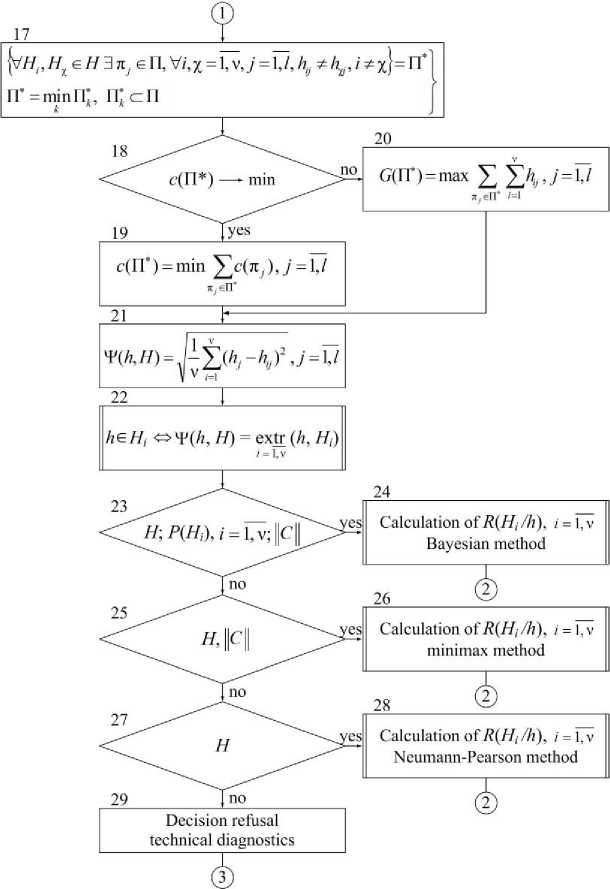
The requirements for optimization of the set of checks are presented on the basis of the condition of pairwise distinguishability of the TS of the system, supplemented by restrictions on finding the optimal subset П ^∗ ⊂ П, such that the formulations [12] presented in operator 17 are resolved.

Operator condition 17 defines a given number of checks required to determine the i -th TS of the system and requires that in the required subset P^* there is at least one check π j , such that any two dictionaries DS H i и H χ , ∀ i , χ = 1,ν, i ≠ χ , were pairwise distinguishable by the results of this check and so that this subset was the minimum of all possible ones.

In the general case, several subsets P*, can be found that satisfy the condition of operator 17. For the final choice of one of these subsets, operators 18– 20 additional specific optimization requirements are formulated.

Optimization requirements are expressed in minimizing the total costs associated with performing checks π j , included in the desired optimal subset P^* (operator 19) or in maximizing the reliability of recognition of failures when performing checks π j , included in the sought optimal subset P^* (operator 20). When requesting a minimum of total costs associated with performing checks included in the desired subset P^*, operator 18 transfers control to operator 19, and, if necessary, to ensure maximum reliability of failure recognition, to operator.

Operator 21 in each case makes a classifying solution to the problem of recognizing failures by calculating the index Ψ( h , H ) of similarity (measure of proximity) between the vector (5) and each of the classes (2) of the alphabet (3). The use of the proximity measure    Ψ( h ,     H )

in the algorithms for recognizing failures is due to the type of DS used to find the place of failure of systems; therefore, the options for calculating the similarity indicator Ψ( h , H ) for a large number of states are extremely diverse. By decomposing and generalizing the working dependencies proposed in the considered section of the developed algorithm, the arithmetic operations of the operator 21 are reduced to a single scheme for calculating the root-mean-square distance between the image components of the system (5) and the DS dictionary (2).

The decision rule of the problem of classifying the search for the place of failure of the system is presented in the operator 22. The minimization or maximization of the decision rule of the operator 22 is determined by the specification of the types of DS given by the type of system with previously known design features (1).

After optimizing the solution to the problem of finding the place of failure of the system, operators 23–29 are included in the process of functioning of the developed algorithm, designed to make a final conclusion based on the results of the process of technical diagnostics of the system using an assessment of the average risk of decision-making R ( H i / h ), i = 1,ν . Operators 23–29 implement the Bayesian decision-making strategy for technical diagnostics with its required modifications depending on the availability of the initial data and the applied criteria for developing the final decision. Without violating the generality of reasoning, we note the potential of probabilistic decision-making methods when processing, including data of deterministic and logical DS, assuming the values of such DS to be probabilistic, with the probability of occurrence of unity.

Operator 23 checks the conditions for the direct statement of the Bayesian method. When defining the image of the system (5) at the previous stages of the functioning of the algorithm, the stability of the description of the alphabet of classes of the TS of the system (3), the given probabilities of the classes of the TS of the system Р ( Н_i ), i = 1,ν and the probabilities of the appearance of images when the system is in the i -th classes of TS P ( h / H i ), i = 1,ν , the invariability of the payment matrix (4), the operator 24 calculates the average risk of making a decision of technical diagnostics R ( H i / h ), i = 1, ν by direct application of Bayes' theorem [12; 16].

The value of the average risk of making a decision of technical diagnostics R ( H i / h ), i = 1, ν is an indicator by which the final decision is made about the belonging of the recognized state of the system to one of the classes of inoperable states.

In the absence of information about the probabilities of the classes of the TS of the system Р ( Н_i ), i = 1, ν control is transferred to the operator 25, who checks the conditions for the applicability of the minimax method. With the known alphabet of classes of the TS of the system of the form (3) and the pay-out matrix of the form (4), the operator 25 connects the operator 26, which contains the apparatus of the minimax method. The average risk of making a decision R ( H i / h ), i = 1, ν is calculated in this case according to the modified rules of the specified method [6; 15].

Operator 27 is intended for inclusion in the decision-making process of technical diagnostics of the tools of the Neumann – Pearson method. If there is only information about the alphabet of classes of TS of a system of the form (3), the average risk of making a decision R ( H i / h ), i = 1, ν is calculated in operator 28 according to the criteria of the Neumann - Pearson method [15].

Otherwise, the decision on the diagnosis is not made and control is transferred to the operator 29, which performs the process of refusal to make the decision of technical diagnosis.

In order to exclude operator 29 from the structure of the optimal conditional algorithm for finding the place of failure of systems, further improvement of diagnostic knowledge is assumed in the following areas:

• –    justification and acceptance of assumptions about the neglect of losses associated with correct solutions of the TD problem, incomparably small in relation to the losses associated with errors of the I-st and II-nd kind;

• –    estimation of the probability distribution densities for all classes of recognizable states of systems;

• –    introduction into consideration of the so-called threshold value of the likelihood coefficient, which is the ratio of the conditional distribution densities of DS values in the classes of inoperable states systems.

In the developed algorithm, operator 29 is a dead-end test for finding a defect. Information about the absence of a solution related to the most probable place of system failure is transmitted to operator 34.

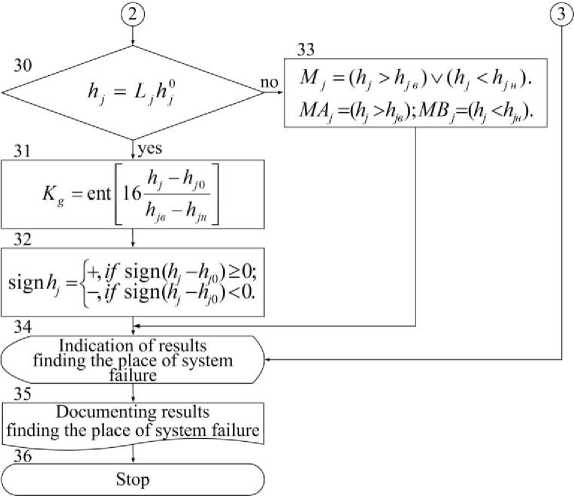
Depending on the requirements, the output of the results of solving the TD problem involves the branching of the developed algorithm by the operator 30 on the line of quantitative or qualitative assessment of the control results.

The structure of the developed algorithm also assumes the presence of a set of control and processing blocks located in a certain sequence, indication (registration) of control results in the appropriate units of measurement of the j -th DS or in the form of logical conditions for the assessment "Defect".

When specifying the requirements for the quantitative (measuring) presentation of the failure recognition results, the assessment of the results of technical diagnostics is expressed by the operator 30 in the form of the number L j , showing the quantitative value of the j -th DS and the unit of measurement of the j -th DS – h ⁰ .

A quantitative approach to recognizing failures involves determining the deviation of the measured value of the j -th DS h j from the nominal h j 0 in the gradations of the tolerance and scrap fields. The value of the gradation in most modern control systems is chosen equal to 12.5% of the half of the tolerance [4]. The measured DS value is considered positive when the tolerance band is exceeded and negative if the measured DS value is less than the tolerance band. Further, the operator 30 includes in the work operator 31, which determines the estimate of the defect of the j -th DS. In operator 31, based on the known maximum permissible upper h jв and lower h jн values of the j -th DS, respectively, by rounding to the nearest number from below (ent), the gradation number K g , corresponding to the DS value is determined.

The sign of the deviation of the measured value of DS from the nominal value is determined using an obvious formula, resolved by operator 32.

When specifying the requirements for a qualitative (tolerance) presentation of the results of searching for the place of system failure, operator 30 transfers control to operator 33.

In case of qualitative recognition of failures, the evaluation of the type "Defect" (D), or "Defect above" (DA), "Defect below" (DB) of technical diagnostics results is carried out by operator 33 by trivial comparison of the measured value of the j -th DS h j with the maximum permissible upper h j в and lower h j н values.

Data of a quantitative or qualitative assessment of the results of solving the TD problem are submitted to operators 34 and 35, intended, respectively, for displaying and documenting diagnostic information.

Development of recommendations for the practical application of solutions

A variant of the practical application of the developed algorithm is possible in the structure of information diagnostic systems related to the typology of artificial intelligence systems [4]. The inclusion of the algorithm in the mechanism for obtaining solutions (solver) of the information diagnostic system eliminates the need to operate with rules - rather voluminous constructions for expressing connections, dependencies between facts and their combinations. Automatic connection of knowledge procedures that allow performing calculations or transformations of functions and making decisions in a certain situation is performed by the algorithm depending on the data of operator 2. Very laborious, especially with large systems, the process of enumerating possible options is eliminated. Consequently, the mechanism for obtaining solutions of the artificial intelligence system containing the obtained algorithm is assumed to be maximally optimized.

In the structure of concepts formed in the form of abstracted systems that have definitions, structures and constituent elements, the initial data indicated above are mandatory, which imposes significant requirements on the amount of permanent memory and the speed of the calculator processor. However, this drawback is less significant in comparison with the advantages of the proposed approach. Moreover, the resources of the information diagnostic system are freed up by the absence in its structure of complex models for representing the knowledge base and the rules involved in the derivation - the so-called production models and semantic networks [4].

Conclusion

The resulting set of prescriptions determines the optimal sequence of actions of performers and means necessary and sufficient to recognize failures with minimal costs and (or) maximum reliability of control of TS systems. The operations of recognizing unworkable states of the system are defined as multi-step actions to transform the input information about the DS into the output one, which is a conclusion about which class of TS the system image belongs to.

Thus, using the proposed algorithm, there is no the need for combination and unconditional checks of system elements and at the same time predetermines the possibility of research, primarily of elements with low reliability.