Change in magnetoresistance in manganese chalcogenides MnSe1-XTeX from bulk to thin-film samples

Introduction . To control spacecraft in extreme conditions with a temperature difference of two hundred or three hundred degrees, it is necessary to create elemental electronic microelectronics that operates in these conditions. Traditional electronics operates on silicon and germanium semiconductors operating with an electron charge. But the electron has a spin and orbital angular momentum, which is used in spintronics, which takes advantage of both non-volatile magnetic memory and high-speed electrical information processing systems. In spintronics [1; 2], to convert an electric signal, not only the charge degree of freedom of an electron is used, but also a spin, which allows creating fundamentally new spintronic devices. The electron has orbital degrees of freedom, acting on which it is also possible to regulate the transport and dielectric characteristics in a magnetic field

In chalcogenides, there is a relationship between the parameters of the magnetic and electrical subsystems [3–7] and the effect of magnetoresistance [8–12]. To date, manganese oxide compounds (manganites of the LaMnO₃ type) [13–17], europium chalcogenides, CdCr 2 Se 4 , and HgCr 2 Se 4 selenides [18–20] are being intensively studied. In the MeXMn1-XS sulfide systems (Me = 3d metal) synthesized on the basis of α -MnS monosulfide and undergoing the metal – insulator transition [21–24], the CMR effect was found to be comparable with its value in manganites [25–28].

Manganese chalcogenides MnSe and MnTe are antiferromagnets (AFM) and undergo structural and magnetic transitions with an increase in the degree of hybridization of manganese cations with Se and Te anions [29; 30]. The change of the transport properties from the semiconductor to metal at the temperature near the room one. MnTe crystallizes in a hexagonal structure of the NiAs type [29]. Mn manganese monoselenide MnSe exhibits a structural phase transition from the cubic phase to the NiAs structure in the temperature range 248 K <  T < 266 K [30], and below this temperature phase coexistence is observed in the sample.

The antiferromagnet MnTe consists of ferromagnetically ordered spins in the plane that are oriented antiferromagnetically along the hexagonal axis. The spins are located in the base plane and have anisotropy of the light plane type with a Néel temperature T = 340 K [31]. For MnSe, the Néel temperature in the cubic modification is TN = 135 K, and in the hexagonal NiAs phase it coincides with the structural transition temperature TS = 272 K. Manganese chalcogenides are semiconductors with p – type conductivity, which have an energy gap in the spectrum of single particle electronic excitations for MnSe (2.0–2.5) eV and MnTe (0.9–1.3) eV with polaron type charge carriers [32]. The effect of magnetoresistance in a magnetically ordered cubic phase was detected on MnSe samples when approaching the Néel temperature with the electrical resistivity ρ = 104 – 103 Ohm ∙ cm [33]. A decrease in the metal – anion Mn–Te bond length, according to theoretical calculations of the band structure [34], induces a change in the crystal structure from hexagonal to cubic with antiferromagnetic ordering with a binding energy of one Mn–Te pair EZB, H = -0.31 eV/bond with bond length RAF = 2.70 Å, and with ferromagnetic ordering EZB, H = -0.51 eV/bond with RF = 2.71 Å. In the

NiAs structure, the bond length is R(Mn–Te) = 0.273 Å. The lattice constant a = 5.44 Å in MnSe with a NaCl structure is somewhere in the middle between 2RF and 2RH; therefore, when selenium is replaced by tellurium at low concentrations, the formation of Mn-Te-Mn ferromagnetic bonds with anisotropy of the light plane type is possible. As a result, the formation of the angular phase and enhancement of the magnetoresistive effect in anionsubstituted MnSe 1- X Te X solid solutions are possible. Substitution of selenium with tellurium leads to suppression of the hexagonal phase and to the single-phase state of the MnSe 1-X Te X system with a face-centred cubic structure with space group (225) [35] in the temperature range 120 K <  T < 300 K and in the concentration range 0.1 ≤ X ≤ 0, 4 [36]. Local non-correlated lattice deformations are possible, which will cause a change in the electronic structure and a change in resistance during the hopping type of conductivity along with changes in the magnetic properties [37–38].

The aim of this work is to detect the magnetoresistive effect and to elucidate the microscopic mechanism of the influence of the magnetic field on the transport properties of MnSe1-ХTeХ solid solutions (0.1 ≤ X ≤ 0.4) based on a comprehensive study, electrical resistivity, currentvoltage characteristics and optical absorption spectra depending on temperature and magnitude of the magnetic field.

Materials and research methods. The electrical resistivity is measured by a standard four-probe compensation method using direct current in the temperature range 77–300 K in a magnetic field of up to 13 kOe. Fig. 1 shows a temperature dependence of the resistance of MnSe 1-X Te X solutions for all compositions (0.1 ≤ X ≤ 0.4). At T <  T N , a deviation from the linear dependence lnρ = lnρ 0 + Δ E / T is observed. The activation energy Δ E ≈ (0.07–0.09) eV is practically independent of the composition in these samples.

The effect of a magnetic field on transport properties was investigated in two ways. First, the change in resistance was measured by the temperature of MnSe 1-Х Te Х solid solutions located both in a magnetic field and in its absence. Secondly, at a fixed temperature, the currentvoltage characteristics were studied in a zero magnetic field and in a field H = 13 kOe. Fig. 2 shows the currentvoltage characteristics of manganese chalcogenides MnSe 1–Х Te Х for composition X = 0.1 at temperatures (100, 140 and 190 K). The U ( I ) dependences are linear and independent of the magnitude of the magnetic field at T < 100 K. It was established that the resistance of the samples decreases in the magnetic field and the greatest change (about 100 %) was found in the neighbourhood of the Néel temperature for a composition with X = 0.1 (fig. 3, a ). For a concentration with X = 0.2, a decrease in resistance was found in the paramagnetic region at a temperature above the Néel temperature and in the temperature range 160 K <  T < 270 K is 5 % (fig. 3, b ). For high concentrations, magnetoresistance (MR) was not detected.

The magnetic moment of the samples was measured in a magnetic field of 0.8 T in the temperature range 80 K <  T < 700 K in two modes: cooling in a zero magnetic field and in a magnetic field of 0.8 T.

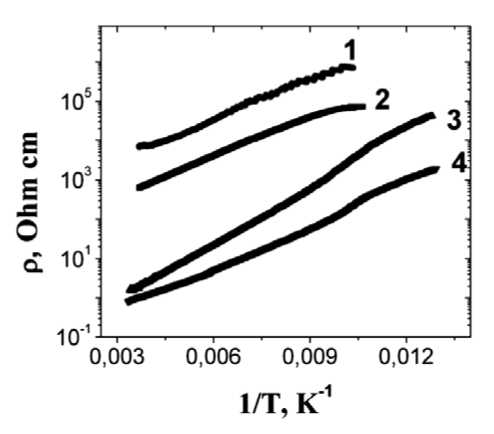
Fig. 1. Temperature dependence of the electrical resistivity MnSe 1– X Te X solutions with concentration of X = 0.1 (1), 0.2 (2), 0.3 (3), 0.4 ( b )

Рис. 1. Температурные зависимости удельного электросопротивления для твердых растворов MnSe_{1– Х} Te _Х с концентрацией замещения

Х = 0,1 (1), 0,2 (2), 0,3 (3), 0,4 ( b )

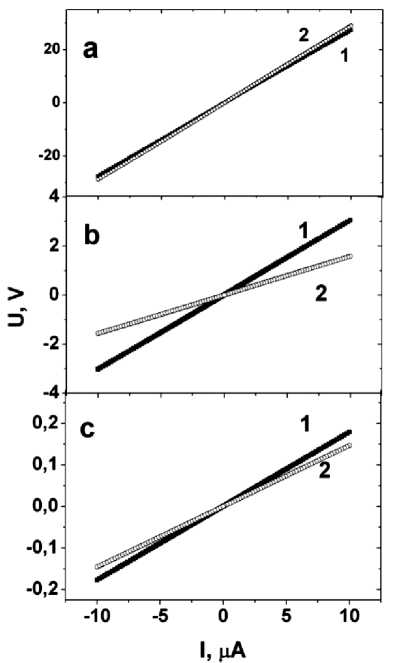
Fig. 2. The current-voltage characteristic of the MnSe 1-X Te X solid solution ( X = 0.1) in a magnetic field H = 1 T (2) and in a zero magnetic field (1) at different temperatures T : 100K ( a ), 140K ( b ), 190K ( с )

Рис. 2. Вольт-амперная характеристика твердого раствора MnSe 1- Х Te Х ( Х = 0,1) в магнитном поле Н = 1 Т (2) и в нулевом магнитном поле (1) при разных температурах Т : 100 К ( а ), 140 К ( b ), 190 К ( с )

The dependence of the susceptibility on the history of the sample was found. Thus, the susceptibility of a sample cooled in a magnetic field is lower compared to a sample in a zero field. The relative change in the magnetic moment (σ (Н)-σ(0))/σ(0) is shown in fig. 3 (curves 3 and 4) and is in qualitative agreement with the temperature behavior of the magnetoresistance.

For X = 0.1, the relative change in the magnetic moment sharply increases in the neighbourhood of the Néel temperature and decreases in absolute value at T = 220 K, where the magnetoresistance disappears. For a composition with X = 0.2, a quantitative agreement is observed between the change in the magnetic moment and magnetoresistance as a function of temperature. The paramagnetic Curie temperature (θ), determined from the high-temperature inverse susceptibility, gradually decreases with increasing concentration of tellurium. In the molecular field approximation, θ = 2/3 S ( S + 1)zJSe for MnSe and for low concentrations, the paramagnetic Curie temperature of the MnSe_1-XTe_X solid solution can be represented as θ = 2/3 S ( S + 1)(zJSe(1 – x ) + JTex) or the normalized dependence θ(x)/θ(MnSe) = 1 + x (λ – 1) is used to determine the sign of the exchange J(Mn-Te-Mn). The fitting functions with the ratio of the exchange parameters λ = J(Mn-Te-Mn)/J(Mn-Se-Mn) = –1.25 and –0.25 describe the experimental results well. For concentrations X <0.3, the sign of the exchange interaction changes to ferromagnetic with a decrease in the exchange value with increasing bond length, according to the theoretical prediction [34].

The formation of polarons or regions with a high concentration of electron density can be traced from the optical absorption spectra shown in fig. 4 for compositions X = 0.2 and 0.4 in the energy range 2000–12 000 cm–1. Electromagnetic radiation can be absorbed by charge carriers during interband transitions, free charge carriers within the same energy zone and crystal lattice vibrations. The low-energy absorption spectrum provides information on phonon spectra and plasmon vibrations in semiconductors, in the high-energy region, on the band gap, on the structure of the valence band and the conduction band near their extrema. For frequencies ω < 5000 cm–1, an increase in the absorption of electromagnetic radiation is observed, caused by an increase in the electron concentration and metallization of the samples. However, these compositions of MnSe1-XTeX solid solutions retain the activation type of conductivity. A sharp decrease in the absorption intensity below the maximum with energy ω = 9700 cm–1 for X = 0.4 corresponds to the band gap of MnTe ω = 9100 cm–1. Those. at this concentration, Mn-Te-Mn bonds flow along the lattice. Near the bottom of the conduction band, additional absorption maxima are observed with ω1 = 6300 cm–1 and with ω2 = 8700 cm–1, located in energy below the bottom of the conduction band by ΔE1 = 3400 cm–1 and ΔE2 = 1000 cm–1. Possibly, these lines correspond to bound states of an electron and a hole, which form a hydrogen-like spectrum of excitons. The spectral line energies are described by the formula Еn = 1.2–0.42/n2 eV with exciton binding energy Еb = 0.42 eV. We estimate the exciton radius from the formula Rn = n2εmaB /μ, where m is the mass of a free electron, aB is the Bohr radius of the hydrogen atom, ε is the high-frequency permittivity for a small-radius exciton ε = 8 for MnSe [39], μ is the reduced electron and hole mass. For μ = 0.5m, the exciton radius is R1 = 0.8 nm = = 1.4 Å. Small-radius excitons move through the Mn-Te system and, at different effective masses of the electron and hole, contribute to the conductivity.

Magnetoresistance model. When anionic substitution occurs, chemical pressure and a change in the crystal field of the octahedron arise as a result of the difference in the ionic radii of selenium and tellurium. At low concentrations, when the octahedron consists of five selenium atoms and one tellurium atom, the bond lengths in the octahedron become not equivalent, which leads to a local increase in the crystal field and a change in the electron density between t 2 g and e g orbitals, i. e. to the formation of an electron on the t 2 g orbital and a hole on the e g orbital and to a change in the spin state of manganese ions in the neighbourhood of tellurium ions. The sign of the exchange interaction will also change as a result of the double exchange of electrons in e g orbitals and the kinetic exchange in the t _{2 g} subsystem. Distortion of the octahedron induces the splitting of t 2 g and e g orbitals with different projections of the +– L^z orbital momentum onto the selected axis. The energy of the deformed octahedron decreases as a result of the rotation of the octahedra in the temperature range 200–250 K depending on the tellurium concentration and with a further decrease in temperature, it is possible that the manganese ions shift with a local change in the lattice symmetry, for example, of the orthorhombic type.

The microscopic model can be represented as ferromagnetic clusters in the neighbourhood of tellurium ions with a random orientation of the anisotropy axes and with orbital moments. In the MnSe 1-X Te X solid solution, we distinguish two temperature ranges, for X = 0.1 in the vicinity of the Néel temperature and for X = 0.2 in the paramagnetic region above the Néel temperature. For a composition with X = 0.1, the magnitude of the ferromagnetic exchange in the clusters exceeds the antiferromagnetic exchange in the MnSe matrix and an angular phase forms with a random orientation of the weak magnetic moment in the cluster in the antiferromagnetic region. When heated, the interaction between the clusters decreases, and the magnetic moments are oriented in the direction of the magnetic field, as a result, the ferromagnetic spin-spin correlation function along the transverse components of the spin increases, and the correlation radius increases. Above the Néel temperature, spin-spin correlations and the correlation radius decrease as a result of thermal fluctuations of the spin moment. In the off-diagonal Anderson model, this corresponds to a change in the width of the potential well and is associated with the temperature dependence of the electron localization radius in the form ^ = A |1 - T / T_N\ . The magnetoresistance in semiconductors, the conductivity of which is described in a model with a variable jump length, has an exponential dependence

(p( H )-p( 0)) / p( 0) = exp (- BH ^)-1 =

= exp ( - BH /|(1 - T / T n )| ) - 1, ^G)

where B is the parameter, H is the external magnetic field, ξ is the electron localization radius [40, 41]. The experimental data on magnetoresistance are satisfactorily described in the framework of this model with a field H = 0.8 T and a parameter B = 0.13 T^–1 for T >  T N , and B = 0.05 T^–1 in the magnetically ordered region. The fitting functions are shown in fig. 3, a , curve 5.

For the composition X = 0.2, the magnitude of the ferromagnetic exchange is much smaller than the antiferromagnetic interaction and the electrons are localized within the lattice constant, in potential wells, the width of which is fixed and the potential barrier varies with temperature. Here, one can use the model of tunneling of spin polarized electrons between potential wells in the form

(р(H)-р(0))/р(0) = 1/(1 + xP1 P2cos9)-1, (2)

where x is the concentration of the wells, P 1,2 is the degree of polarization of the electrons, the angle θ between the axes of polarization of the electrons. The spin polarization of electrons is due to orbital ordering. Suppose that the polarization value P 1,2 is the same for all clusters and disappears at a temperature of orbital ordering T ₀ according to a power law P 1 ₂ = P ₀(1 - T / T ₀ )^1/4. To qualitatively understand the processes of electron tunneling between clusters with polarization axes are in the range of angles from 0 < θ < π, we consider a simple model when the anisotropy field H A is parallel to and orthogonal to the external magnetic field. As a result of competition between the Zeeman interaction and the anisotropy field, the electron spin (polarization direction) will rotate in the direction of the external magnetic field with increasing temperature.

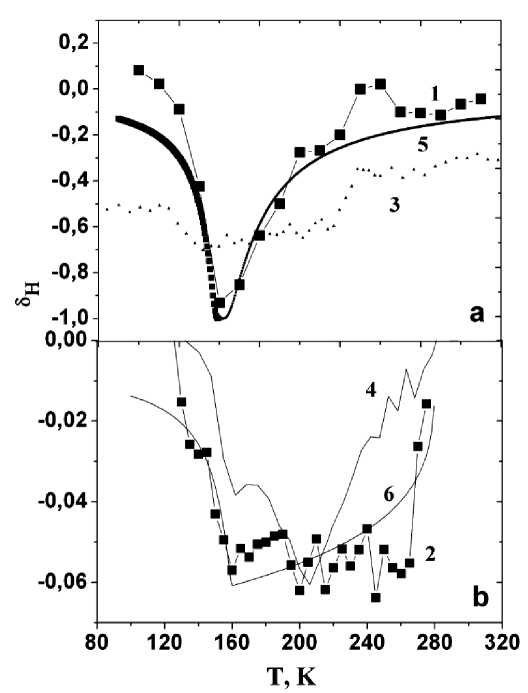
Fig. 3. Temperature dependences of the magnetoresistance of MnSe 1- X Te X chalcogenide with X = 0.1 (1) ( a ) and 0.2 (2) ( b ) at H = 13 kOe. The relative change in the magnetic moment σ (Н) – σ (0) / σ (0) for X = 0.1 (3) and X = 0.2 (4). Fitting functions: for a concentration of X = 0.1 (5) from equation (1) at H = 0.8 T, B = 0.13 T^-1 in the region of T >  T N , and B = 0.05 T–1 in T <  T N ; for X = 0.2 (6) from equation (5) with parameters T 0 = 280 K, T * = 160 K, n = 2/3, λ = 0.1, cluster concentration x = 0.08

Рис. 3. Температурные зависимости магнитосопротивления халькогенида MnSe 1- Х Te Х с Х = 0,1 (1) ( a ) и 0,2 (2) ( b ) при Н = 13 кЭ. Относительное изменение магнитного момента σ (Н) – σ(0)/σ(0) для Х = 0,1 (3) и Х = 0,2 (4). Подгоночные функции: для концентрации Х = 0,1 (5) из уравнения (1) при Н = 0,8 Т, B = 0,13 T – 1 в области Т >  T N , и В = 0,05 T–1 в Т <  T N ; для Х = 0,2 (6) из уравнения (5) с параметрами T ₀ = 280 K, T * = 160 K, n = 2/3, λ = 0,1, концентрация кластеров х = 0,08

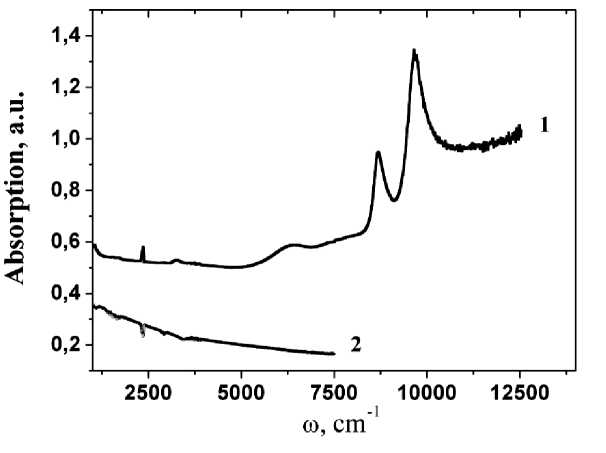
Fig. 4. Optical absorption spectra for MnSe_{1– X} Te _X solid solutions with X = 0.2 (1), 0.4 (2) at T = 300 K

Рис. 4. Спектры оптического поглощения для твердых растворов MnSe_{1– Х} Te _Х с Х = 0,2 (1), 0,4 (2) при Т = 300 К

The correlation between the spins is determined by orbital ordering. The energy of the magnetic system has the form

E = - SH cos 9- SH A cos ( y-9 ) ,         (3)

where HA is the anisotropy field, γ is the angle between the external magnetic field and the anisotropy field. The minimum energy value is achieved at an angle of:

cos 9 = 1/ ^ ( 1 + H A sin² у / ( H + H A cos y ) 2 ) .     (4)

The anisotropy field decreases with increasing temperature according to a power law in the form H A = K (1 – T / T *) ⁿ , where T * is the temperature at which the anisotropy field caused by rhombic distortion disappears. The ratio of the magnetic field to the anisotropy constant is denoted by λ = H / K . Then the temperature dependence of the magnetoresistance is presented in the form