Channel Aware Power Allocation and Diversity Gain Selection for Mimo Noma System

NOMA, a technique in 5G wireless communication systems, has emerged as a strong contender. This paper introduces resource allocation methods that seamlessly integrate NOMA with MIMO systems. In our research, we introduce an uncomplicated approach to diminish the intricacy of the fairness scheduler. We introduce an iterative method for power allocation based on water-filling, customized for the Single User MIMO scenario. Through simulations, our innovative power allocation technique demonstrates improvements in user experience during challenging channel conditions and overall fairness among users [1]. Consequently, there is a pressing need for significant enhancements in QoS, system capacity and overall user experience [2]. Furthermore, future communication systems face the challenge of spectrum scarcity, requiring them to utilize available spectrum resources more efficiently [3]. In mobile communication systems of 4G, such as Orthogonal Multiple Access (OMA), LTE-Advanced using OFDM for downlink and Single Carrier Frequency Division Multiple Access (SC-FDMA) for uplink transmissions has been the standard. However, as we transition to 5G systems with their need for high throughputs, it becomes necessary to depart from traditional OMA approaches [4].

NOMA introduces the novel concept of concurrently multiplexing distinct users on the same sub-band in the power domain, extending the principles of the OFDM layer [5]. By utilizing the spatial multiplexing capabilities inherent in MIMO channels, higher data rates can be achieved while maintaining constant bandwidth consumption. Thus, the adoption of MIMO technology is essential in addressing the challenges posed by mobile communications of future generations [6].

This basic primary focuses of paper is developing the scheduling techniques for a downlink single-user (SU) MIMO system based on NOMA principles. While many NOMA papers depend on the (PF) proportional fairness scheduler, which strives to strike a balance between system capacity and user fairness, its application in the SU-MIMO NOMA context is complex due to the need to evaluate user set combinations of numerous candidate. In our work, we adopt an enhanced version of the PF scheduler, recently introduced to reduce complexity by minimizing the number of candidate user sets during allocation. In the realm of allocation of power, earlier works often assumed a same distribution among sub-bands and transmit antennas [7]. Our work seeks to extend this principle to SU-MIMO systems, building upon a recent iterative water filling technique proposed for single-input-single-output (SISO) systems.

The paper structure unfolds as follows: Section 2 offers a related work, Section 3 presents the improvements to the scheduling algorithm and the proposed power allocation method in SU-MIMO, Section 4 conducts a comprehensive analysis of the performance of these approaches, Section 5 provides the results and discussion, Section 6 gives the paper's conclusion and lastly declarations section is declared from the authors side.

2.    Related Works

In real-time applications, only NOMA-OQAM implements the orthogonally property, which has an impact with inherent imaginary ISI on both the symbols received and the essential receiver functions. While NOMA-OQAM ensures precise synchronization thanks to its exceptional feature localization, it additionally presents inherent disturbances in the realm of complexity because of the lack of orthogonally [8, 9]. To address this issue within the NOMA-OQAM system, authors in [10] proposed coordinated beam forming to facilitate multi-user MIMO signals, reducing intrinsic interference. Additionally, in [11], the authors presented a system that utilizes the Viterbi algorithm to eliminate partial approximation interference with a simplified complexity. The results reported in reference [12] illustrated that the channel estimation method introduced in the study showed improvements in aspects like intrinsic interference and power efficiency when contrasted with method i.e auxiliary pilot channel estimation. As a result, the method outlined above can be considered a more effective strategy for tackling of intrinsic interference problem in NOMA-OQAM.

This method employs the modulation index, as presented by the authors in [13], to mitigate the impact of intrinsic interference on the overall system performance. Additionally, it incorporates a gray code constellation for mapping specific bits and considers their Hamming distance, resulting in an improved Bit Error Rate (BER) at the receiver in NOMA IM. In [14], to tackle the challenge of multi-dimensional residual interference in NOMA-QAM the authors introduced a maximum likelihood detection method to tackle the challenge of multi-dimensional residual interference in NOMA-QAM. Their proposed receiver system is MIMO-based, aiming to boost BER performance while carefully considering computational complexity. Furthermore, in the study conducted by the authors of [15], a linear transformation technique based on Singular Value Decomposition (SVD) is employed to convert overlapping symbols in modulated NOMA into independent parallel transmissions, effectively achieving this transformation. The presented method demonstrates a linear enhancement in performance metrics such as Bit Error Rate (BER) and Out of Band Emission (OOBE) when employing QAM order, as opposed to traditional NOMA QAM methods.

In [16], the authors introduced an iterative intrusion cancellation technique designed to remove Inter-Symbol Interference (ISI) and Inter-Carrier Interference (ICI) in NOMA QAM systems. This intrusion cancellation process disassembles data received, splitting it into odd-numbered sub-carriers and even-numbered and, effectively mitigating impact of interferences on system performance. In order to mitigate the impact of interference in NOMA-QAM systems, the authors of [17] have introduced weighted vectors specifically designed for Minimum Mean Square Error (MMSE) equalization. This research assesses the influence of non-orthogonal filters on Bit Error Rate (BER) performance. Additionally, the study conducted by the authors in [18] aims to minimize non-orthogonally, mitigate BER degradation, and improve the performance of NOMA QAM by harnessing a range of prototype filter, including Isotropic Orthogonal Transformation Algorithm (IOTA) and Square Root Raised Cosine (SRRC). Recently, the effective implementation of QAM in conjunction with NOMA has been employed to reduce intrinsic interference. In reference [19], the authors have put forth power restrictions and performance criteria for the fifth-generation network system, which presents various challenges such as energy consumption, consolidated transceivers, and reduced complexity importantly, these techniques deviate from traditional methods. Within wireless communication, orthogonally plays a pivotal role by mitigating interference issues and elevating the QoS.

Furthermore, the system development utilizing more antennas has emerged due to the significant increase of endusers number of. All these users must be taken into account, together with escalating data rates and the demand for high traffic rates [20, 21]. The researchers [22] effectively reduced intrinsic interference in the NOMA QAM system by employing coordinated beam forming with MIMO, allowing the transmission of signals in [23] the authors introduced a system that employs the Viterbi algorithm to eliminate partial approximation interference while reducing complexity. In comparison, reference [24] showcased enhancements of the presented channel estimation method performance, especially in aspects such as intrinsic interference and power efficiency, in contrast to the auxiliary pilot channel estimation method. Addressing the challenge of multidimensional residual interference in NOMA-QAM, the authors of reference [25] put forward a maximum likelihood detection approach. This work also presented a receiver system based on MIMO, enhancing Bit Error Rate (BER) performance while considering computational complexity. Furthermore, to address challenges related to orthogonally and quality degradation, [26] introduced the NOMA QAM framework employing a pre-coding method.

3.    Wireless Systems in Multiple User Environments

Wireless systems for multiple users incorporated into multiuser networks, NOMA exhibits a low out-bandemission profile, resulting in a less favourable network performance. Utilizing a multiuser access network, however, enhances spectral efficiency by enabling more flexible system resource allocation. Within the context of a multi-user environment, the multi-user detection system can distinguish and identify individual user data. Additionally, it is feasible to adjust the offset frequencies of different users to improve orthogonally, as discussed in reference [26]. Stringent synchronization is essential to establish orthogonally in a multi-user environment. Traditional equalization methods of NOMA systems are highly valued. Spectral filtration within NOMA serves to minimize signal disruptions among non-synchronous users. Employing NOMA with QAM improves system performance and reduces interference. However, it's worth noting that for future generations, the system may still face challenges due to substantial QoS delays. Channel equalization plays a crucial role in optimizing Bit Error Rate (BER) within Multi-User Multi-Input. In proposed MIMO NOMA system optimal power allocation is employed by combing channel metrics and statistical characteristics of each user at the uplink side as shown in fig.1. And the overall system performance is improved using optimal Maximal ration combiner (MRC) and ML based multi user detection at the downlink side as shown in fig.2. To suppress the co-channel interferences successive interference cancellation is incorporated which will decode the strongest signal first and decode all other successive signals based on prior references. The improvement in transmission and reception of data rates within the channel leads to an enhanced data rate. The channel attenuation is heightened, resulting in a significant increase in the QoS. This is particularly evident in the modelling of compact devices within the 5G model.

Substantial gains can be achieved through the utilization of the conventional MIMO system. When dealing with a linear channel featuring a high Signal-to-Noise Ratio (SNR) gain limit, the multiplexing gain is likewise elevated. Regarding the uplink aspect of Multi-User (MU) MIMO, the antenna arrays are segmented into independent regions, marking a departure from the behaviour of traditional MIMO systems. It's important to note that the presence of the Doppler Effect and limited diversity in channel delay spread can lead to Outperforming conventional MIMO systems in terms of performance. The limited diversity, which results in outperformance compared to conventional MIMO systems, is closely tied to the number of antennas and leads to a significant drop in efficiency. Here is a list of the advantages of MU-MIMO.

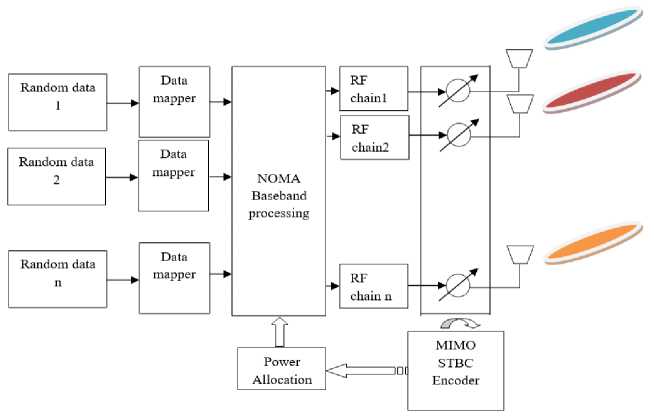
Fig.1. MIMO NOMA Uplink block diagram

To ensure robustness in the overall Multi-User MIMO (MU-MIMO) system, it is crucial to suppress Co-Channel Interference (CCI). This suppression aids in mitigating selective fading within the channels. In the context of MU-MIMO systems, Multi-Packet Reception (MPR) is utilized in WLANs. In established systems, short data propagation intervals causing interference can generate high throughput for Single-User MIMO (SU-MIMO), MU-MIMO attains a greater throughput rate while minimizing the probability of collisions. In order to sustain adequate data rates, a mathematical model, as introduced in reference by M. M. Al-Wani et al, has been suggested to calculate the necessary energy allocation levels.

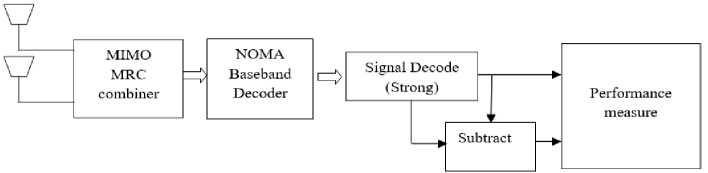
Fig.2. MIMO NOMA dowlink system using SIS interference cancellation scheme

In this research, a precise beam forming vector is employed to estimate the probability, this estimation is then employed to regulate and oversee the transmitted power of the system. As the number of antennas in user equipment (UE) increases, the radio frequency chain of the base station becomes increasingly intricate, leading to increased power consumption and heightened computational overhead. To enhance the performance of multiple-user MIMO systems, employs Semi-blind Channel Estimation to identify active users Furthermore, at the quantized data converters, base station, as discussed in reference [12], are deployed to lower hardware complexity, enhance energy efficiency, and alleviate the impact on QoS levels. The Linear-Quantized Pre-Coder (LQPC) is utilized to assess the performance of low-resolution data converters in the presence of distortion, and its design is centred on MMSE considerations.

Table 1. System parameters

No. of Users	Links used in the design	Modulation technique used	Length of FFT points	Latency formed in each Channel	Product of latency and power in channel	Speed	Type of mode
6	10	32 QAM	32	1/6	e-p/3 Where p=0 to 9	3-120 km/hr	ITU vehicular type B
8	12	64 QAM	64	1/8	e-p/2 where p=0 to 9	3-100 km/hr	ITU vehicular type B
10	14	128 QAM	128	1/10	e -p/1.5 where p=0 to 9	3- 90 km/hr	ITU vehicular type B

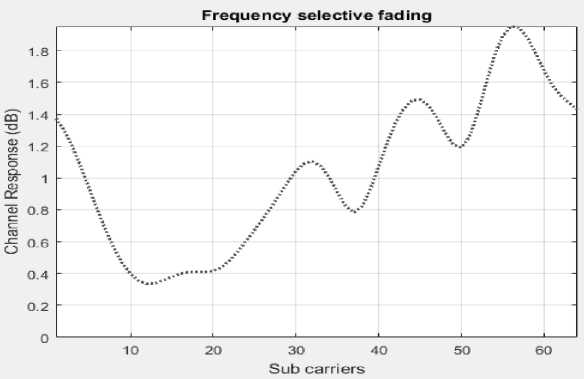
Fig.3. Performance of channel response and frequency selective fading for sub-carriers

The primary drawback of QAM-based NOMA becomes evident when the channel exhibits time selectivity, which adversely affects the orthogonally of the subcarriers, primarily due to the presence of ICI as depicted in fig.3. The channel's non-linearity is added with Gaussian channel noise, forming a distinctive channel parameter that encompasses co-channel interference and symbol interference. A uniquely identifiable data channel is present in every multipath element, collectively composing a channel matrix. The experimental results, along with the performance of the employed machine learning techniques, are evaluated using a frequency-selective channel model, and the outcomes are presented in fig. 3. The relationship between the doppler factor and the spread delay metrics is efficiently leveraged and various measurements, including power delay profiles and path mapping rates, are tabulated for different individuals within the multi-user environment, as detailed in table.1. This table underscores that in a non-linear channel; channel interference and ISI symbol are more noticeable, further emphasizing the importance of a real time for multiuser data environs. This empirical data helps confirm the performance metrics of the MU-MIMO system.

4.    Proposed 64-QAM NOMA System

In comparison to CP-OFDM, NOMA offers enhanced orthogonally. NOMA employs offset QAM modulation techniques for signal processing, thereby optimizing spectral efficiency and mitigating multi-carrier interference issues. True orthogonally in NOMA-OQAM effectively addresses intrinsic interference, as represented by equation (1), this term defines discrete NOMA symbols of the baseband modulation.

X[n] = E M-o¹ I N-¹ a d,k X [n - yM ] e ^j2M k ^(n-2)ejek,d

y[n] =∑ i^P=^-0¹ ∑ j^Q=^-0¹ b j,i Y[Q- ^xP e ^j2 P ^π(Q-a 2 ^)ejθj,i ]

The length of the FFT denoted as 'P'. X[n] is the value of coefficient. yM/2 is delay time. The phase term is indicated as e^(jθk,d), and b (j,i) represents the OQAM real values. The received signal is derived from Equation (1) through the inner product of y[n] and the latency version of b (j,i) , which is denoted as Y[n].

r k,d = ∑ n⁺=^∞-∞ y[n]. g ^∗ k, Y[n]

^rd,k ^{= b}j,i ^{+ ∑+}m^∞=-∞ ^Xd,k^Xd^∗,k^[n] )

Equation (4) demonstrates the summation of imaginary-valued intrinsic interference, which arises due to the use of complex-valued QAM, which introduces orthogonally challenges. While there are resemblances between the proposed framework and the current NOMA/QAM framework, a key distinction lies in the receiver end, where the channel possesses perfect state information. The input for each block consists of a complex value, and NOMA/QAM plays a role in improving intrinsic interference. By factoring in cost considerations for orthogonally, the NOMA/QAM system bolsters system stability.

• 4.1.    Orthogonally

Orthogonally plays a crucial role in the Multi-Carrier Modulation system, as it is essential for recovering the transmitter symbol. In the case of complex orthogonally in OFDM, this is accomplished by employing a rectangular pulse in the time domain of the system. This pulse also serves to gradually decay the frequency ambiguity function. Orthogonally is commonly maintained over dispersive channels by cyclically applying OFDM, especially when the Cyclic Prefix (CP) exceeds the channel impulse duration. In challenging channel conditions, preserving the transmitted symbol's orthogonally can be quite demanding. To guarantee orthogonally, NOMA is utilized to configure the filter, and the configuration relies on the modulation technique in use. Real or complex values can be assigned to the data as required. In NOMA system modulated signal generates some integer multiples of signal beams (frequency bins (0…N-1)) by performing power allocation at each time samples k for different users as given below.

x(n) =∑ n^N=^-0^{1 √αnPn} xk(t), 0≤k≤N-1

The N point DFT of a signal x[n] is formulated as

X(k) = ∑ n^N=^-0¹ x(n)W N^kn , 0 ≤k≤ N-1

W N = e ^-j2π⁄N

Here an IFFT is performed for sub carrier mapping followed by base band signal processing block which exploits both the symmetry and periodicity properties of the twiddle factor. The spatial frequency index k decides the projection of RF beams and its relationship with the given antenna gain ϴ s is described as follows:

2П.k/L=q.d.ϴ s -L/2 ≤ k ≤ L-2/2

Where q is referred to uplink transmission antennas

The antenna gain difference between two angular RF beam angles is directly related to the spatial frequency bin separation as given below:

θ

s

λ

Nd cos θs

rad

This can be changed at the uplink side by using optimal STBC encoder and associated combining techniques at the receiver side.

• 4.2.    Equalization of Channel

In conventional NOMA-OQAM, time-frequency localization is notably effective, albeit with minimal Out of Band Emission (OOBE) characteristics. However, Challenges emerge as a result of Inter-Symbol Interface and Inter-Carrier Interface, which gradually erode OOBE orthogonally with increasing channel time and frequency selectiveness. In the context of addressing Frequency Selective Fading in the system, it's important to note that the channel response is never uniform (flat), rendering channel equalization a particularly intricate process. Introducing MIMO to NOMA optimizes enhances bandwidth efficiency and inter-antenna interference, although it also adds complexity to the task. Evaluating the equation's efficiency in terms of frequency selectivity is essential. In the MIMO NOMA/OQAM framework, the channel selection for pregnancy cannot be made arbitrarily; there are restrictions in place.

The goal of adaptive equalization is to improve the performance of equalizers, both linear and non-linear, in constantly changing channel situations. An adaptive equalizer adapts to the communication channel's time-varying characteristics automatically. It is assumed by this strategy that there are temporal irregularities in the communication route. It attempts to create an equalization filter whose coefficients dynamically adjust in response to changes in the channel with the goal of real-time mitigation of additive noise and inter symbol interference. Adaptive equalization operates on the implicit premise that a channel will vary gradually over time. Furthermore, the constrained value range of NOMA contributes to enhanced resistance to frequency variations caused by the Doppler spread. In the equalization, the proposed system demonstrates the performance in terms of convergence to update adaptive decision equalizer filter and its transfer function in communication channel is given below

1-1.1:t-1+04x-2+03x-3+01X-4+0.05x-s001:r-60.02:t-7

This equation is equalized by the adaptive decision based equalizer with coefficients 0(li) = [0 1 (к),.... ,0_N(k)]^r . The response of channel frequency with y(k) is an uncorrected sequence in binary on values ± and its channel output is corrupted by additive zero mean AWGN noise with variance of 0.0001. The signal-to-noise ratio (SNR) of the channel output is estimated to be around 45 dB. The adaptive equalizer, with a length of N=10, enables flawless zero-forcing equalization. This equalizer is implemented using one of the adaptive filters explored in this chapter as in fig. 4.

Adaptive D e cision Biter based Equalizer

Nonlinear function

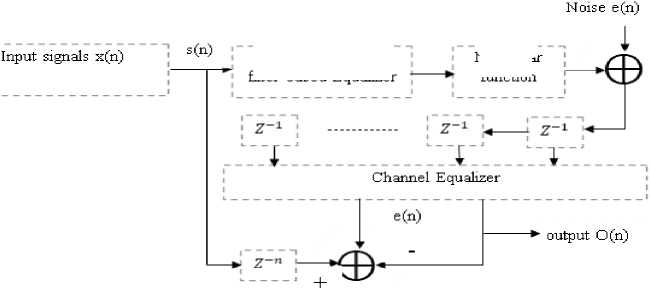
Fig.4. Proposed Adaptive Decision channel equalization to remove ISI symbols caused by linear channel

The output of this equalizer O(n) for N-tap equalizer is given by

^ k-k₀   X n=0 ^ nk ^ k-n

Where R_k-n is received signals k_ko is delays introduced by systems. Adaptive equalizers update the coefficients, represented by Cnk, periodically to reflect the current channel characteristics. The determination of equalizer coefficients can be based on the channel response, the training sequence, or directly from the data sequence.

• 4.3.    Frequencies-selective Channels

• 4.4.    Channel Selection based Latency

• 4.5.    Successive Interference Cancelation (SIC)

NOMA stands out as a robust system with versatile applications, serving three distinct purposes: Ensuring dependable communication over time, managing dispersive frequency channels, and enabling multiple access systems are common objectives. Both Multi-Carrier (MC) and NOMA systems operate on sound principles to achieve these goals. Compared to CP-OFDM illustrated in fig.5, this system exhibits superior Out of Band (OOB) performance. When transmitting signals over selective frequencies, multi-carrier modulation systems generate ICI and ISI. These effects are particularly prominent in frequency-selective channels, potentially degrading QoS. They partition the spectrum to create numerous narrow channels, and shaping the filters is a critical aspect. One effective technique for this is NOMA in multi-carrier systems, with the Bit Error Rate (BER) for FFT-64 depicted in fig. 6(a) and the BER for FFT-128 shown in fig. 6(b). Traditional equalizers, like MMSE equalizers, can effectively address these issues by minimizing interference in the sub-channels and ensuring a flatter response. When choosing a channel under the influence of Doppler effects, the losses most closely associated with QAM-based and MU-MIMO and MIMO pertain to degradation of the performance, especially in terms of error rates. This becomes especially noticeable when a substantial users’ numbers are vulnerable to co-channel interference. The primary aim of the proposed multiple-user MIMO communication systems is to mitigate the impact of Doppler spectrum normalization on the error rate gap by taking into consideration mobility factors in fast fading scenarios. In contrast to MMSE, ML speeds up the iterative soft decoding process by monitoring variations in the channel.

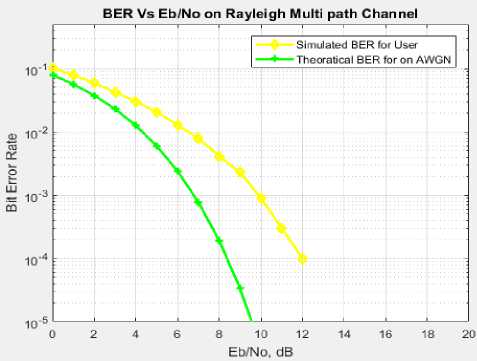
Fig.5. Analysis of BER between theoretical and simulation in NOMA QAM's performance over double delay spread frequency selective channels

The primary focus of this work is on cascaded channel accurate using the MMSE model without introducing any additional design complexity to address RIS matrix formulation and optimal pre-coding for a channel controlled environment. In both the downlink of the synchronous CDMA and the uplink of the asynchronous CDMA system, novel and enhanced blind multiuser detection algorithms are recommend for implementation. The innovative methods efficiently reduce the impact of interfering users by introducing a crucial cross-correlation matrix constraint between neighbouring symbols. This leads to the creation of two improved blind multiuser generalized receivers; each of these receivers is guided by unique sets of optimal criteria and is constrained by the cross-correlation matrix. It's crucial to highlight that the suggested generalized receivers can be employed in a blind manner only when the desired user channel estimation is available. The simulation outcomes reveal a substantial boost in the performance of the recommended improved blind generalized receivers as compared to conventional blind detectors.

In channels with higher levels of selectivity, linear equalizers exhibit a decline in performance, leading to degradation in the desired QoS. This is primarily due to the absence of flat sub-channels, as these channels are inherently frequency-selective. This evaluation is commonly referred to as Bit Error Rate (BER) performance analysis. Specifically, NOMA QAM analysis is conducted in the scenarios involving increased delay within the frequency-selective channel. Notably, ML, MMSE, and BER performance gap analysis widens significantly in the analysed results.

In an effort to diminish the computational complexity associated with signal detection, which scales proportionally with the number of symbols and exhibits exponential growth concerning both the number of users (L) and number of bits per symbol (log2Z, where Z represents the order of the constellation), the following approach is undertaken.

oML

= argMn P - E HR q¹¹

^{R £} S P          q = 1

q = 1

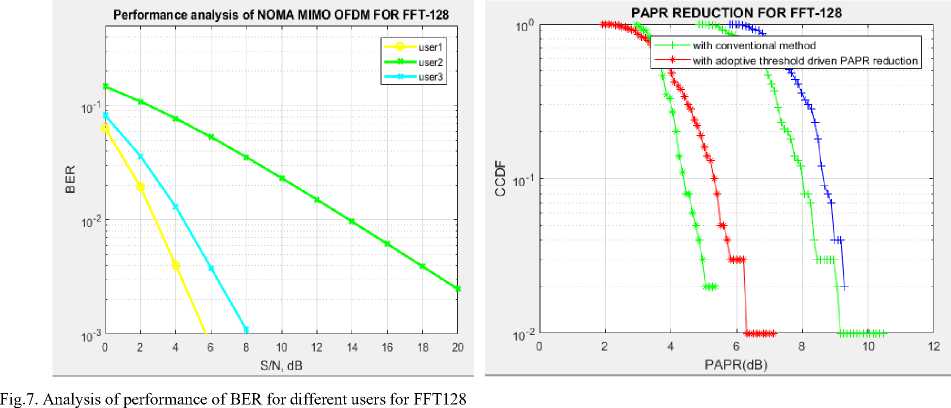
When transmitting signals over selective frequencies, multi-carrier modulation systems generate ICI and ISI. These effects are particularly prominent in frequency-selective channels, potentially degrading QoS. They partition the spectrum to create numerous narrow channels, and shaping the filters is a critical aspect. One effective technique for this is NOMA in multi-carrier systems, with the Bit Error Rate (BER) for FFT-64 depicted in fig. 6 and the BER for FFT-128 shown in fig. 7. Traditional equalizers, like MMSE equalizers, can effectively address these issues by minimizing interference in the sub-channels and ensuring a flatter response.

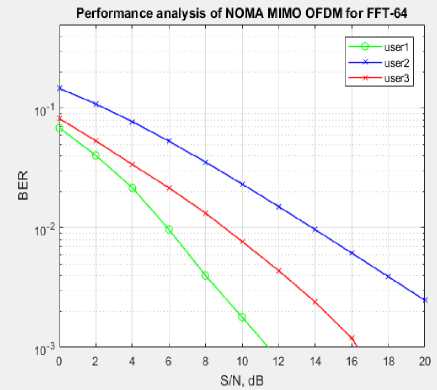
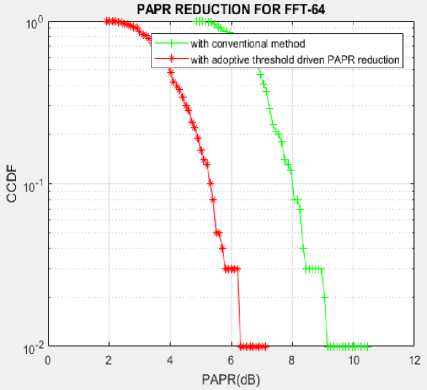
Fig.6. Analysis of BER and PAPR NOMA-MIMO for FFT64

Optimal Decoding Approach:

Input: Vector received Xn ∈ {x1…xr}Nt, H ∈ {i, j} with spatial dimensions Mt x Mr; Output Yn.

• •    During the phase of decomposition, specific points of constellation are chosen to match individual sequence T originating from the input Xn.

• •    Each sub-detector receives Tq and reference values Φn: ∈ {0, 1…n} from Xn and carries out ΦC: (|Φn: ∈ {0, 1…n/4}|). It subsequently determines the sequence with the minimal distance from the identified sequence as described in equation (5).

• •    During the successive decoding phase, weights are computed for detection, and the minimal interference originating from X1… XMt-1 is subtracted.

• •    In contrast to parallel interference cancellation (PIC), achieving optimal performance relies on the assumption that there is at least one candidate present in each successive symbol detection round.

  
  
  
5.    Results and Discussion

In fig. 8, the throughput performance analysis NOMA-MIMO system compared with SISO system is illustrated. The results unequivocally demonstrate that MIMO surpasses SISO performance, particularly at distances below the nominal range (<100m), and it exhibits near-optimal performance as distances extend to 500m. Employing an ML decoder with optimal maximal ratio combining (MRC) within the MIMO framework enables structured results for NOMA. In cases where alternative methods are applied, the proposed systems demonstrate performance enhancements, leading to minimized Bit Error Rates (BER) and overall system performance improvement. Consequently, this aids in recombining ML detectors with the NOMA system, resulting in lower error rates within the simulator, and facilitating comparisons with other substitution methods.

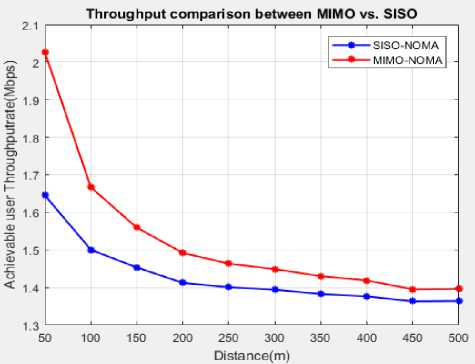
Fig.8. Analysis of the throughput between SISO and MIMO for NOMA system

The channels with higher selectivity, linear equalizers exhibit a decrease in performance, this leads to degradation in QoS. It's important to note that flat sub-channels are no longer available due to this. This performance evaluation is also referred to as Bit Error Rate (BER) analysis. The analysis specifically focuses on NOMA QAM with increased delay in the spread frequency of the selective channel. The results indicate a significant performance difference between ML, MMSE, and BER. Fig. 7 illustrates the throughput performance analysis of NOMA QAM in a fast-fading vehicular channel, comparing MMSE and NOMA QAM decoders. The proposed systems outperform alternative methods, leading to minimized BER rates and improved performance. This optimization involves combining ML detectors with NOMA QAM, resulting in lower error rates in the simulator when compared to other substitution methods.

This research work conducts a comparative analysis and implementation of two methods: MIMO NOMA with a flat fading channel and the same with a Nagakami-m selective fading channel, across various sub-bands and user rates. As the number of sub-bands increases, the proposed MIMO NOMA system consistently exhibits superior system performance, signifying improved results in terms of error rates. The integration of NOMA with Maximum Likelihood (ML) detectors further enhances system performance, leading to reduced Bit Error Rate (BER). The simulation results vividly illustrate how this proposed approach effectively minimizes rates of error when compared to the alternative multiple access methods. Examination is conducted in order to assess the impact of both selective fading and the Frequency Selective Fading Method (FSFM) within the proposed approach. The advanced Maximum Likelihood (ML) detectors exhibit robust behaviour within MIMO NOMA systems. The notation 'θ' is denoted as path-independent delay profile, demonstrates a bigger range of carrier drift across each specific multipath component. Fig.7 illustrates the BER performance rate variations in accordance with the Multi-User MIMO NOMA system suggested rate. The Doppler Effect assessment also addressed and evaluates the performance of mathematical models. Additionally, the MIMO NOMA is analysed for the influence of user rate, as depicted in fig. 9.

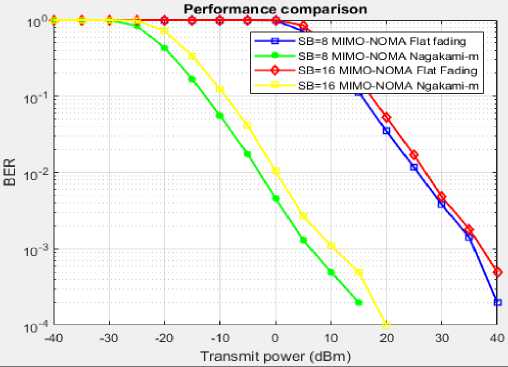
Fig.9. BER performance measurements of Multiple User MIMO-NOMA QAM

Performance Analysis

The MATLAB 17a simulation is conducted for the MIMO NOMA system, taking into account fixed system parameters such as power level and distance. The results obtained from the MATLAB simulations are utilized to assess system performance. The assessment of the suggested MIMO NOMA system is conducted to identify any potential drawbacks. Fig.10 illustrates the performance analysis, specifically comparing different users in the MIMO NOMA system based on Bit Error Rate (BER) parameters. Furthermore, table 2 presents a simulation and comparison of NOMA QPSK with varying power levels, highlighting the alignment of each user's power level with the relevant system performance, in accordance with the recommendations.

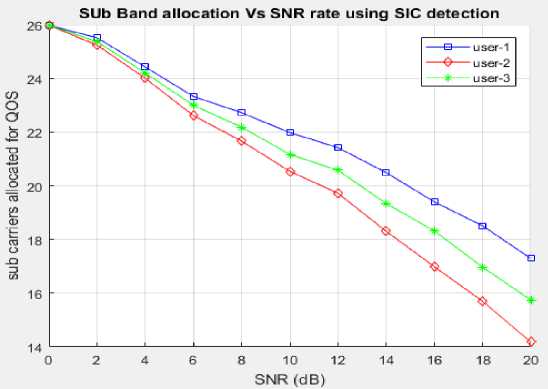
Fig.10. Analysis in terms of QoS and SNR under different QAM modulations between users

Table 2. Comparison between proposed work and existing MIMO system with NOMA system

	Proposed				Existing [6,5,4,1,2,3]
Parameter	SNR(dB)	BER	PAPR	MMSE	SNR(dB)	BER	PAPR
K=4 for 16 QAM	93	0.0019	7.2210	0.0008	90	7.3x10-3	8.43
K=4 under 64 QAM	89.2	0.0089	7.245	0.0013	40[5]	9.3x10-3	8.52
K=4 under 128 QAM	85.2	0.0091	7.500	0.0025	76[6]	9.710-3	8.68

The designed MIMO NOMA system is effectively implemented and simulated within the MATLAB 2017A environment. A comprehensive comparison is conducted between the proposed system and recently published articles, focusing on parameters such as Peak-to-Average Power Ratio (PAPR), MSE, Signal-to-Noise Ratio (SNR) and BER as presented in table 2. The results reveal significant optimization, with a 13% improvement observed in both BER and MMSE compared to existing methods. The proposed system has been simulated under different noisy conditions with dynamically change of QAM bits and measured throughput and data rate. The throughput and date rate are higher as compared to OFDM as shown in fig.11 and fig.12.

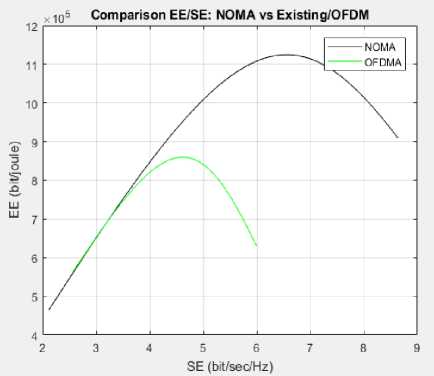
Fig.11. Simulated results of throughput in bit/sec/Hz

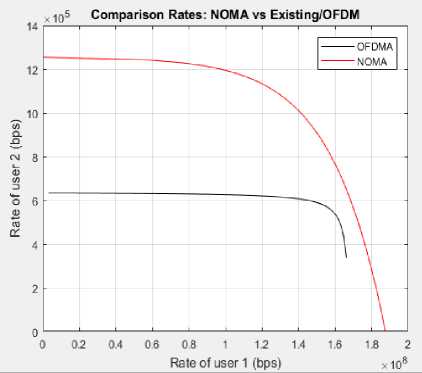
Fig.12. Simulated results of data rate in bps

6.    Conclusions

This work primary focused on NOMA and OFDM for reckoning task offloading in terms of high energy efficient and high throughput. This paper is centred on assessing the performance metrics of a MIMO NOMA system that employs power domain multiplexing for users sharing the same channels. This is accomplished by employing superposition power allocation at the transmitter and successive interference cancellation (SIC) at the receiver. The study assesses the performance trade-off concerning different power levels and corresponding travel distances. The experimental results conclusively demonstrate the significant impact of power allocation on achievable system performance. Additionally, the importance of MIMO becomes evident, particularly in scenarios characterized by selective fading, and the resulting performance penalty gap with sub-band allocation is also confirmed. The allocation of power and MIMO antennas to each user can be tailored to their specific channel conditions. Finally simulated results are compared with recently projected works and found that BER and PAPR are optimized around 6% to 8% and throughput and SNR are improved by 12%.

Acknowledgements

We would like to give thanks to the School of Electronics and Communication, REVA University, Bangalore granting access to the experiments and LAB Data sets.