Chaotic Genetic-fuzzy encryption technique

Nowadays, data such as digital images, audio, video becomes a vital resource of communication. There are many intruders and attackers try to unauthorized access sensitive data. Therefore, the need to build robust and efficient security techniques for protection of digital data during transmission or storage them over the internet is vital demand [1-2]. A possible traditional solution is a cryptography. It is the science to encrypt and decrypt data to transmit or store sensitive information over insecure networks so that only the intended recipient can read it. Encryption technique type may be symmetric that uses only one secret key for encryption and decryption or asymmetric that uses one secret key for encryption and another key for decryption [3]. The key length and operation’s functions are important characteristics that determine the strength and efficiency of encryption technique. A strongencryption technique must verify confusion and diffusion requirements and resistant to cryptographic attacks. Thetraditional encryption techniques like DES, AES, IDEA, RSA, etc. are used and gave good results [1- 5]. In [6], Symmetric Key Encryption Decryption using modulo 69 is proposed for encryption and decryption process.

Using traditional encrypting techniques in real-time multimedia applications suffers from high computing power, large computation time and high expenses. Hence, it demands bettersolutions to resolve the security problems of multimedia data effectively [7].The authors described an approach for high-quality image hiding by improving the visual quality of the stego-image with large embedding capacity [8]. In [9], Omar A. Dawood and et.al., proposed Tigris cipher based on secret-key block cipher to protect privacy and resist attacks. This cipher applies essentially four functions to produces an adequate security with minimum encryption time. These functions are XORed, S-box tables, row shifting and mixing each column in the matrix operation.

In [10], an extension of Hill cipher by generating dynamic encryption key matrix is proposed to provide more effective in the encryption quality of RGB images.

Authors Proposed encryption algorithm for enhancing the security level of the encrypted image that comprises two phases: fuzzy logic system and genetic algorithm that generate key value [11]. Authors proposed ascheme to enhance securitylevelfor image encryption based on thesecret sharing concept, fuzzy logic technique and AES algorithm [12].

Paper [13] proposed an algorithm to generate server public and private keys using fuzzy logic for decreasing encryption and decryption processing time. The author proposed a modified pixel-chaotic-shuffle mechanism for color image encryption based on multi-chaotic systems for improving security level [14]. The authors proposed encryption and decryption methodology for enhancing the security by adding layer of security to encode of characters that is performed based on magic rectangle. This methodology is acting as a wrapper to any public key cryptosystems for enhanced security [15]. For enhancing image encryption, the algorithm by dividing it into a number of blocks based on the Fuzzy sets is proposed [16]. In [17], a technique-basedon Fuzzy approach, variable multiple rights translated AES Gray S-boxes and steganography technique for gray image encryptionis presented that has high resistanceagainst computational attacks. An iterative symmetric encryption algorithm based on a combination of bit permutations andchaotic function to enhance digital data securityis presented in [18].

The paper evaluates and analyzes image encryption techniques that are proposed in the literature and verify their characteristics to determine the Strength, efficiency and weaknesses of these encryption techniques [19].

The authors introduced DNA Encryption and Decryption Algorithmby generating a DNA encoding table for encoding of secret data, division, rotation and transformation [20-21].

In [22], the author proposed DNA-Genetic Encryption Technique based on the multi-stage and genetic operations torealize a great confidentiality system.

Many cryptosystems implement simultaneously confusion and diffusion stages for strong encryption effectand high security. Image encryption algorithms using the chaotic map to shuffles the pixel positions and modifies pixel values in plain-image to get unrecognizable image   [23].   Fridrich, J. [24]

proposedencryption algorithm to image using two-Dimension chaotic map. Design image cryptosystems using three-Dimension chaotic map to improve encryption efficiency anddecreases processing time are proposed in [25-28].

This paper proposes Chaotic Genetic-fuzzy Encryption Technique(C-GET) that is an iterative symmetric technique to encrypt a secret data. C-GET depends on standard chaotic, chaotic Henon map, some of the mathematic operators, fuzzy logic system and genetic algorithm operations. C-GET composes of pre-processing, symmetric key encryption and genetic-fuzzy operation encryption stage. In this technique, the secret data converted into binary. In addition, generate chaos functions values related to predefined initial values then create appropriate fuzzy members and fuzzy rules based on experience. Each round has multiple operations dependent on chaotic map values. In addition to that, the symmetric key is used. Anydata type format can be used as secret data i.e. text, word document, image pixels, audioandvideo. The color and gray images offer an excellent digital data to test any encryption technique so; they are used for testing the efficiency of the proposed technique. Experimental results prove that typical copy of secret data is reconstructed. They also show that proposed technique improves encryption efficiency. The remaining of this paper is organized as follows: the proposed technique is introduced in detail in section 2; the experimental results are presented, discussed and evaluated in section 3. The obtained security results are satisfied. Finally, the last section gives concluding remarks.

• II.    Chaotic Genetic-fuzzy Encryption Technique

The main objective of all security techniques is to protect information and data from any attacker activities. Due to increasing of computing power, time and computational complexity are two significant parameters those making security algorithms strong and unbreakable. The symmetric cryptography technique is an iterative process, which is proposed to encrypt a secret data. The proposed technique is depended on the standard chaotic function, chaotic Henon map, some of the mathematic operators, fuzzy logic system and genetic algorithm operations. Any digital data type (i.e. message, signal, image or video) can be encrypted. The main steps of the proposed technique are pre-processing, symmetric key encryption, and genetic-fuzzy operation encryption stage. They are explained as follows.

• A.    Pre-processing Stage

After reading secret data, this data must be prepareddependingon its type. In case of atext file, it is converted into ASCII values. Group them into 8-bits binary data. In case of a gray image, read pixels of image data into 8-bits Binary data. In RGB image, first, it is separated into three components. As it is known, a classic video includes many frames. Separate one frame at a time. The same steps of the gray image is applied for every RGB components and each video frames. After grouping secret data (message, image, video or signal) into bytes, convert it into two-dimension (2D) matrix.

• B.    Encryption Stage

The original input data is treated as a simple 2D matrix composed of bits “0” and “1”. After read the secret data, encrypt it using a standard chaotic function given by:

f(x) = Ax(a - x)

With λ value between 3.57 and 4 [29] and a is approximately equal one. The chaotic behavior of such a function has been widely studied. The chaotic system is sensitive to a very slight change in initial condition or parameters.

Generate chaotic random values equal the size of 2D matrix then, perform an exclusive OR operation on the corresponding elements of them.

• C.    Genetic-fuzzy Operation Encryption Stage

Another chaotic function is used to define the number of iterative process, positions’ index and the type of operations that are executed. This is a two-dimensional chaotic map that is called a Henon map (HM) and its equations are:

x(n + 1) = y(n) - bx2(n) + 1y(n + 1) = cx(n)

When using this map, initial values and the parametersmust be set, the system behaves as a chaotic system when b = 1.4 and c = 0.3 [30].

This chaotic system generates a chaotic sequence of real random numbers. These real numbers are transformed to a sequence of unsigned random numbers byusing the following equation:

x(n) = x(n) + max(-x(n)))x(n) = round(d * (x(n))

Conversion unsigned random numbers ( x ) to the approximate size of 2D matrix that represents encrypted secret data with suitable d value.

In general, the encryption system consists of two stages: replacement of datavalues called confusion and modification of data values called diffusion. To execute confusion and diffusion, the proposed system defines a number of operations based on the mathematic operator, fuzzy logic and genetic algorithm stages.

It is known that fuzzy concepts first introduced by Zadeh in the 1960s and 70s and Fuzzy logic attempts to reflect the human way of thinking. In a global sense, fuzzy logic is approximately identical with the fuzzy sets theorem, which relates to classes of objects with un-sharp boundaries in which membership is a matter of degree [31-32]. Types of Fuzzy algorithms arerelational algorithms that describe a relation between fuzzy variables and can be used to approximately describe behavior of a system and decisional algorithms type which describe a strategy for performing some task. Fuzzy logic algorithm composes from the following steps: fuzzify step that converts input values into fuzzy membership functions, compute the fuzzy output by executing appropriate rules in the rule base and defuzzify that estimates crisp output values .

In the first step of the fuzzy algorithm, divide the two-dimension secret data into a number of classes, which represent Fuzzy sets. Define the linguistic variables of fuzzy sets that are sharp or un-sharp boundaries. There are many different membership functions such as triangular, trapezoidal, piecewise linear, Sigmoid, Gaussian, Z-shaped curve, Pi-shaped curve, S-shaped curve or singleton. As an example, figure 1 shows the membership functions.

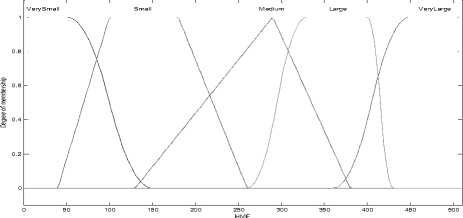
Fig.1. Membership Functions

Before construction the rule base, a number of functions based on mathematics, genetic algorithm (GA) and fuzzy logic operators. The GA includes the following operations: selection, crossover (single point …) and mutation [33]. These operations are functions that representing the individual transformations. Two random values are generated based on Henon mapping and other predefined values. The first random value is called position index that defined that start point of operation. The second random value ( n ) defines the number of operation’s reiteration.

position = modulus(x(n), predefined, value)n = modulus(x(n),predefinedvalue)

Selection position must cover all data. The position value selects data for performing some task. A number of functions; that may use in the proposed system; are explained in the following:

• •    Rotate up ( rotU(i1,pos+1,n) ): rotate 2D secret data’s row up from row index(position) with n rows.

• •    Rotate bottom ( rotB(i1,pos+1,n) ): rotate 2D secret data’s row bottom from row index with n rows.

• •    Rotate right ( rotR(i1,pos+1,n) ): rotate 2D secret data’s Column right from Column index with n Columns.

• •    Rotate left ( rotL(i1,pos+1,n) ): rotate 2D secret data’s Column left from Column position with n Columns.

• •    Row Complement   ( compR(i1,pos+1,n) ):  bit

complement 2D secret data’s row value from row position until row index equal the addition of position and n value.

• •    Column Complement ( compC(i1, pos+1,n) ) : bit complement 2D secret data’s Column pixel from Column position until Column index is (position + n) value.

• •    Column Crossover   ( crossC(i1,pos+1,n)):  two

Columns (position and position +1) are selected. The position is a single-point crossover point is determined then, exchanging the heads of two Columns. In next step, repeat the following n-times, increase column number with one, select this column and next column and swap two heads of columns at position index.

• •    Row Crossover ( crossR(i1,pos+1,n) ): two rows (position and position +1) are selected. Determine a single-point crossover point position then, exchanging the heads of two rows. In next step, repeat the following n-times, increase row number with one, select this row and next row and swap two heads of rows at position index.

• •    Row mutation   ( mutateR(i1,pos+1,n)) :  change

values (position) with value of any linear function. Repeat this operation n-time.

• •    Column mutation   ( mutateC(i1,pos+1,n) ):repeat

change values (position) value of any linear function for n-times.

• •    Row addition ( addR((i1,pos+1,n) ): add two rows (position and position +1). In next step, repeat the following n-times, increase row number with one, add two rows (position and position +1).

Row(pos)=(double(Row(pos)) + double(Row(pos+1)) > 255) * (-255) + (double(Row(pos)) + double(Row(pos+1)))

• •    Column addition ( addC((i1, pos+1,n) ): add two Columns (position and position +1). In next step, repeat the following n-times, increase Column index with one, add two Columns (position and position +1) as the following equation:

Column(pos)=(double(Column(pos))+double(Col umn(pos+1))>255)*(-255)

+(double(Column(pos))+double(Column(pos+1)))

• •    Row subtraction   ( subR((i1,pos+1,n) ):  subtract

row(position+1) from row(position). In next step, repeat the following n-times, increase row index with one, subtract row (position+1) from row (position).

Row(pos)=(double(Row(pos))- double(Row(pos+1)) < 0 )*(256) + (double(Row(pos)) -double(Row(pos+1)))

Or subtract row(position) from row(position+1)

• •    Column subtraction ( subR((i1,pos+1,n) ): subtract Column(position+1) from Column(position). In next step, repeat the following n-times, increase row index with one, subtract Column(position+1) from Column(position).

Column(pos)=(double(Column(pos)) -double(Column(pos+1)) < 0 )*(256) + (double(Column(pos))-double(Column(pos+1)))

It is also used other operation that enhancing encryption process i.e. row/column subtraction from or addition to pseudo-random sequences, chaotic Henon mapping values.

• D. Fuzzy Rules Construction

Expert knowledge is made decisions as group of if…..then….. statements. Many necessary rules can be written to describe the system adequately and to cover all data. The Fuzzy rules are built dependent on Henon mapping and other predefined values. The condition may be modulus or other operation of Henon mapping values with boundaries Fuzzy sets. Then determine position and n values and apply one or more pre-defined functions, i.e. rotate right, Row subtraction, Column Complement. The rule may have single condition or two conditions. The sample of rules as follows:

if modulus(x(i),val) >=115  && HMF  input is

VerySmall ;

then determine position and n values and apply rotU(i1,pos+1,n);compR(i1,pos+1,n);crossC(i1,pos +1,n);

if modulus(x(i),val) >=105 && HMF input is Small ;

then determine position and n values and apply rotB(i1,pos+1,n); compC(i1,pos+1,n);

if modulus(x(i),val)>= 90 && HMF input is Medium ;

then determine position and n values and apply rotR(i1,pos+1,n); compC(i1,pos+1,n);

if modulus(x(i),val )>=70 && HMF input is Large ;

then determine position and n values and apply rotL(i1,pos+1,n); compR(i1,pos+1,n);

if modulus(x(i),val) >= 35 &HMF input is VeryLarge; then determine position and n values and apply rotB(i1,pos+1,n); crossC(i1,pos+1,n);

if modulus(x(i),val) >= 0;

then determine position and n values and apply rotU(i1,pos+1,n); rotL(i1,pos+1,n);

crossR(i1,pos+1,n);

Execution of this process simultaneously mixes the properties of confusion and diffusion that are required to obtain a high-security level. The stages of C-GET are illustrated in figure 2.

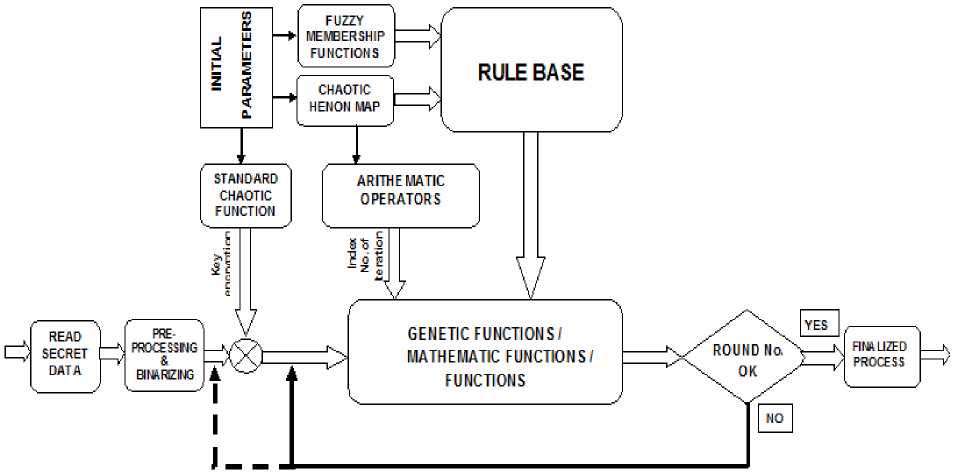
Fig.2. Stages of C-GET

Input: Read Secret data (text/Image/…).

Output: encrypted (text/Image/….) file

BData1 ^ Binarize the secret data.

Pre-processing Bdata1

BData2 ^ 2D Matrix (Group 8- bits)

F(x) ^ Generate random values using standard chaotic function

EncryptData ^ F(x) XOR BData2.

X ^ Generate random values using Henon chaotic map function

While (Round Number not equal to Zero) do if rem(x(i),val) >= fuzzy set boundary(1)*xxx; then determine position and n values, for n times, select and execute one or more operations.

else if rem(x(i),val) >= fuzzy set boundary(2) *xxx; then determine position and n values, for n times, select and execute one or more operations.

else if rem(x(i),val) >= fuzzy set boundary(n-1) *xxx; then determine position and n values, for n times, select and execute one or more operations.

else determine position and n values, for n times, select and execute one or more operations.

End while

Reshape EncryptData

Save encrypted (text/Image) file

Transmit file.

• Fig.3.    Pseudocode of Proposed Encoding C-GET

Input: encrypted (text/Image/….) file

Output: secret data

BData1 ^ Binarize encrypted (text/Image) file

Pre-processing Bdata1

BData2 ^ 2D Matrix (Group 8- bits)

F(x) ^ Generate random values using standard chaotic function

X ^ Generate random values using Henon chaotic map function

While (Round not equal to Round Number) do if rem(x(i),val) >= fuzzy set boundary(1)*xxx; then determine position and n values, for n times, execute one or more operations elseif rem(x(i),val) >= fuzzy set boundary(2)*xxx; then determine position and n values, for n times, execute one or more operations elseif rem(x(i),val) >= fuzzy set boundary(n-1)*xxx; then determine position and n values, for n times, execute one or more operations else determine position and n values, for n times, execute one or more operations

End while

EncryptData ^ F(x) XOR BData2.

Reshape EncryptData

Save re-constructed (text/Image/….) file

• Fig.4.    Pseudocode of Proposed Decoding C-GET

The Pseudocode of Encoding and Decoding secure C-GET are shown in figure 3 and figure 4.

In the previous explanation of C-GET, the preprocessing stage depends on each type of data file and format. It is wide-ranging among to conversion to ASCII values, reading pixels of the image, separating components or frame and getting the properties of the video file as mentioned above to solve this problem, generalize C-GET technique. The generalization technique is composed of the same stages of C-GET but, the process of read data and the pre-processing stage are replaced with a simple read binary file command (fread) using 8-bit unsigned integer (uint8) and specified parameters that describe the format of the secret data.

• III.    Implementation and Evaluation Results

  The C-GET is implemented using MATLAB 2012 on Windows 8.1 64-bit Operating system in AMD Athlon (tm) II X2 220 Processor, 2.80GHz and 4 GB RAM. We perform number of experiments to test and evaluate the effectiveness of the proposed technique and run it with different types of secret data. We use different sizes images, for example, to check the technique performance by testing encryption strength and original image recovery. The strength of encryption is been evaluated using two of the most common quantity; the number of pixel changing rate (NPCR) and the unified average changed intensity (UACI) [34-35]. Peak signal-to-noise ratio (PSNR) is used to test image quality.

In the first part, some experiments are carried out to prove the efficiency of the proposed C-GET with different formats of gray and color images. We choose some known test images and others as test images. First, read image.

In case of RGB image, separate firstly it to three components, then each component passes through the processes of C-GET to encrypt it. After encoding, gathering, reshape and save encrypted data in file. The original images and encrypted-images in image format are shown in Figure 5. The processing time for encrypting 256x256 gray image file is approximately 0.5 seconds/256 rounds. The processing time for encrypting 256x256 RGB image file is approximately 3.3 seconds/256 rounds. Some gray and true color images and their encrypted images format are shown in figure 5.

original image

original image original image original image

image format image format image format image format

Fig.5. Original Images and Their Encrypted

Fig.6. Encrypted Images with Uncover All Data with Fuzzy Rules

In case of insufficient representation, rules and the rules do not cover all data size; the encryption technique has a very low-security level and is not good technique. Some examples of encrypted data are shown in figure 6 due to using the encrypted technique with lack of rules and uncover all data with fuzzy rules.

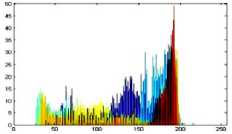
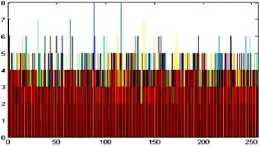
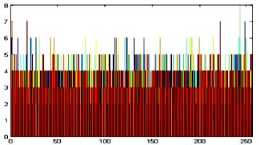
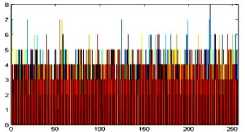
Histogram Analysis

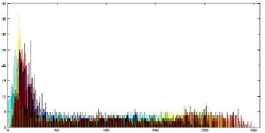
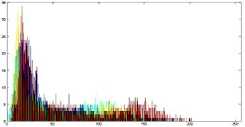
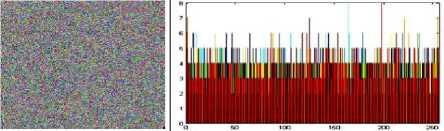
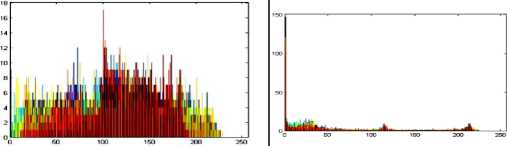
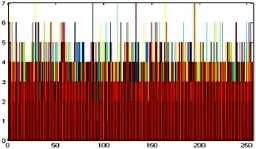
The histogram is a graphical representation that shows the occurrence of pixels intensity values. To prevent an attack, the obtained cipher image should give no indication about the original image. In the proposed approach, the obtained cipher image does not give any indication of the original image, whichis analyzed through histograms. A sampleof gray and RGB images, corresponding encrypted images and their histograms are shown in figure 7.

Original image

Original image Histogram

Original image Histogram

Original image Histogram

Encrypted image

Encrypted image Histogram

Encrypted image Histogram

Encrypted image Histogram

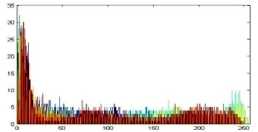
Original image          SOriginal image R Histogram

Original image G Histogram          Original image B Histogram

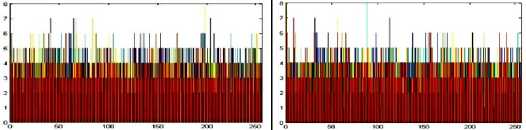
Encrypted image        Encrypted image R Histogram

Encrypted image G Histogram        Encrypted image B Histogram

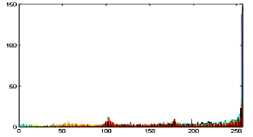
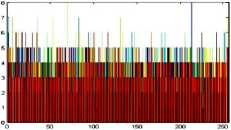
Original image

Original image R Histogram

Original image G Histogram          Original image B Histogram

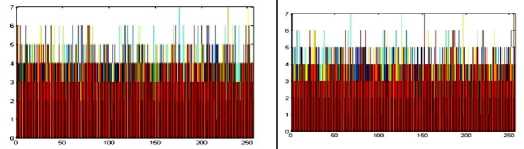
Encrypted image

Encrypted image R Histogram

Encrypted image G Histogram

Encrypted image B Histogram

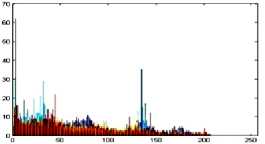
Original Gray image

Original Gray image Histogram

Encrypted Gray image

Encrypted Gray image Histogram

Fig.7. Original Image, Histogram of original image, Encrypted Image and Histogram of Encrypted Image

Correlation Coefficient Analysis

The correlation among neighboring pixels for the most part of the original images is high, while the correlation is a little between adjacent pixels in the encrypted image [36]. The following equationdefinescorrelation coefficient:

correlation coefficient =

Z m Z n (A mn -ACB mn -B)

J^ m S n (A mn A) (B mn Bp

correlation coefficient is around zero at highly uncorrelated sequences. In addition, the correlation coefficient almost equal to one when there is strongly correlated sequences.

By using MATLAB function (corr2 (I, J)), the correlation coefficient equals value in range -0.0029 to 0.0059. It is mean that the relation between the original and encrypted imagesis negligible and the encrypted imagedoesnot give any information to the attacker about the original image. This elimination correlation between pixels indicates efficient encryption technique.

Entropy

Entropy is a numerical measure of randomness or disorder in any system that uses to describe the texture of the input image. The following equation defines Entropy:

Entropy = - £ P log2 (P)

Where; P contains the histogram counts.

The entropy is the randomness or uncertainty measure in a secret data, as entropy approaches 8, there is more randomness [37]. Entropy values of the original image and its correspondent encrypted image have been given in figure 8. The obtained results provide evidence that our proposed technique has the ability against entropy attack.

Original image		Original image Entropy	Encrypted image	Encrypted image Entropy	Original image		Original image Entropy	Encrypted image	Encrypted image Entropy
		7.3051		7.9973			6.6782	я® У .■y^Iv.	7.9975
v- .^ - '-^s		7.5269		7.9972			7.8076		7.9991
;ш LUt'l		6.9449		7.9991			6.9449		7.9991
		6.9449	■■■■■	7.9990			7.0404		7.9991
					^^^^1
		7.0404		7.9991			7.3608	1#ийбЙ8Ж _	7.9991

Fig.8. Entropy Analysis of Original Image and Its Correspondent Encrypted Image

NPCR and UACI Analysis

Two parameters number of pixel changing rate (NPCR) and unified average changed intensity (UACI) confirms the ability of proposed technique of resistance against differential attacks. NPCR is the change rate of pixels in the encrypted image when changing only one pixel of the original image and defined as follows:

NPCR(A,B) = -^(£iJsim(i,j)) x 100%

And sim is represented by Equation:

.          (1 if A(i,j) = B(i,j)sim(i,j) =

L 0 if A(ij) * B(i,j)

UACI measures the percentage differences between the original intensity and encrypted image intensity that using the following Equation:

UACI(A,B) = — |£_zy | ^A(U)— ^ |} x 100% mxnl ⁷ Imax _pixel_valtie\J

Where A, B are two corresponding the original and encrypted images to same original image, m and n are dimensions of A and B, and max_pixel_value denotes the

Fig.9. Two Encrypted Images Corresponding to Change 1 pixel in Original Image before Encryption

These parameters are used for testing the effect of changing of a single pixel in the original image on the encrypted image. They also used to test and verify its’ resistance to the differential attacks [26, 29].

Key Space Analysis

The C-GET has large key space that making brute force attack is infeasible Because of using more than chaotic faction type. It's known that the chaotic system is sensitive to a tiny change in initial condition or parameters and fuzzy rules also have several different values that add space to key size and different combinations of them. So it resists the exhaustive of brute force attacks.

Thus, the C-GET makes larger statistical changes in the transmitted images. A cryptosystem is secure if it cannot be discovered even with full knowledge of the decryption algorithm. The gotten results prove that proposed technique can overcome many known and existsteganalytic attacks. Its output depends on initial parameters of chaotic map functions and types of fuzzy memberships, fuzzy rules, operation functions and sequence of functions execution that making a prediction of original secret data is very complex and an increase of computing time. It has a higher level of security against some existing attacks based on the multiple-operations, fuzzy-genetic operations and number of rounds. In general, it realizes better encryption.

• IV.    Conclusions

In this paper, C-GET is designed and implemented. The C-GET enhances secured encryption technique based on multi-iterations, two types of chaotic map functions, fuzzy logic and genetic operations. It is also included mathematic operations, encryption and rotation increase encryption quality. The results show the resistance of the C-GET technique against different attacks based on several parameters, operations sequence of C-GET. The original and reconstructed images are identical. The encrypted-data is more randomness and has negligible correlation with original data so the cryptanalysis’ possibilities for breaking the cipher are negligible. Furthermore, the technique has multilayer protection stages that achieve confidentiality, gives more security, effectiveness and robustness to data, and protects against detection.

In future work, we will be optimizing and standardizing C-GET and try to reduce the transmitted data size and the encryption time.