Частица со спином 1 и аномальным магнитным моментом в кулоновском поле. Нерелятивистская теория

Известно, что в рамках теории релятивистских волновых уравнений можно предложить так называемые неминимальные уравнения, которые описывают частицы с дополнительными электромагнитными характеристиками, со спектрами спиновых или массовых состояний. В частности, интенсивно исследовались [1-11] уравнения для частиц со спином 1, обладающих помимо электрического заряда аномальным магнитным моментом. Уравнение для векторной частицы в случае внешнего кулоновского поля оказывается очень сложным даже в случае обычной частицы без аномального момента. Эта задача все еще не исследована полностью [12]. Однако в нерелятивистском пределе уравнение для обычной векторной частицы в кулоновском поле может быть решено точно. В настоящей работе мы исследуем аналогичную нерелятивистскую задачу для частицы с аномальным магнитным моментом.

Кратко содержание работы сводится к следующему. Исследуется квантово-механическая частица со спином 1 и аномальным магнитным моментом во внешнем кулоновском поле. Исходным является релятивистское уравнение Даффина-Кем-мера, в котором введен дополнительный член взаимодействия, обусловленного аномальным магнитным моментом. На основе диагонализации операторов энергии, квадрата и третьей проекции полного момента выполнено разделение переменных. Выведена система уравнений для десяти радиальных функций. Используя диагонализацию оператора пространственного отражения, разбиваем систему на две подсистемы из четырех и шести уравнений, для четностей Р = (—l)^j+1 и Р = (—1)Л соответственно.

Дополнительные слагаемые, обусловленные аномальным магнитным моментом, присутствуют только в подсистеме из шести уравнений. Эта система уравнений и исследуется. Сначала отдельно рассмотрена относящаяся к классу четности Р = (—1)^J релятивистская система при з = 0. В этом случае задача приводится к дифференциальному уравнению второго порядка. Оно найдено в явном виде и характеризуется очень сложной структурой особых точек.

Чтобы упростить возникающие математические задачи, в радиальных уравнениях выполнен переход к нерелятивистскому приближению. При этом для состояний с j = 0 выведено радиальное уравнение, принадлежащее классу дважды вырожденного уравнения Гойна. Строятся его решения фробе-ниусовского типа. В качестве условия квантования использовано ограничение, выделяющее трансцендентные функции Гойна. В результате получен некоторый спектр энергии, который выглядит физически интерпретируемым, однако получаемые таким способом уровни энергии не зависят от параметра аномального момента, в то же время степенные ряды зависят от этого параметра. Для состояний с большими значениями полного углового момента з = 1,2,... нерелятивистская радиальная система приводится к двум связанным дифференциальным уравнениям 2-го порядка для двух функций. Методом исключения можно получить уравнения 4-го порядка для каждой из этих функций. Исследованы локальные решения Фробениуса возникающих уравнений, сходимость вовлеченных в них степенных рядов с 8-членными рекуррентными соотношениями, а также возможность использования условия трансцендентности для получения спектра энергий.

1.    Разделение переменных в релятивистском уравнении

Исходное уравнение имеет вид (предполагаем использование тетрадного формализма; обозна чения в [13])

^ip^c ре^Зр + |у^аЬ7аЬс(ж)) - в' А,

\X—P_vppl>r^              (1)

где свободный параметр А - безразмерный, Р - проективный оператор, выделяющий из 10-компонентной функции векторную составляющую. Ниже используются обозначения р О

О о е ch’

4а е2

ЛМ’         ПТ'

В сферической тетраде [14] уравнение (1) принимает вид

P°(i3t + |^) + гф3Эт. +

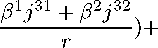
+^м + ^рз03 -м ф = 0>

где зависящий от угловых переменных оператор определен равенством

V                    + У12 COS19

Se = г р дв + р —--—--- sin У

В используемом тетрадном базисе выражения для компонент оператора полного момента имеют шре-дингеровскую структуру [14]:

А = к +

cos). ,12

—рЗ Sint/

42 — к +

sin). ,12

—рЗ sin У

Зз = к, 3^U                         (4)

Ниже будем использовать волновую функцию и явные выражения для матриц Даффина-Кеммера [14] в циклическом представлении, где оператор третьей проекции спина zj12 имеет диагональный вид:

У12 =

0  0   0   0 0  1з   0   0 0  0  1з   0 0  0   0  1з

, ts =

+100 0 0 0 0 0-1

Выражение для проективного оператора Р не меняется при переходе к циклическому базису.

Система радиальных уравнений для обычной векторной частицы в кулоновском поле известна [12]. Чтобы получить обобщенную систему уравнений для векторной частицы с аномальным моментом, достаточно найти явный вид дополнительного слагаемого в уравнении

£р/³ = ^РфОрЗ-рЗрОр (5)

Здесь оператор Pj⁰³ представляет собой матрицу размерности 10, у которой отличны от нуля только элементы (Рз⁰³рз = (^¹у⁰³)з1 = — 1-

Структура 10-компонентной волновой функции векторной частицы с квантовыми числами е, j, т задается соотношениями

После перехода к сферической тетраде, а затем к циклическому представлению матриц Даффина-Кеммера получаем другое представление:

Ф(ж) = {Фо(ж), Ф(ж), Ё(хф Н(х)},

Фо/г) = e-^MrWo.

10  00

0  П3   0     0

0   0 П3    0

0   0   0—П

Ф(ж) = e"^i£t

Ё(х) = e"i£t

Я(ж) = e"^i£t

h(r)D_x

M'r)D0

hhWx

E^D-x E^^Do

Hx^D_x

H^r)D+x

п3 =

0 -1

-1 о о о

где используются D-функции Вигнера D_CT = Е³__т(Т(ф, 9, 0), <7 = 0, — 1, +1. После необходимых вычислений находим систему радиальных уравнений

-(4" + -)^2 - -(Ех + Ез) - ^/₂ = mf₀, dr г г

+г(б + -^Ех + г(4” +     + »"Я2 = г        dr гг

Ёе + “)я2 - г-(Нх - Н3) - ^/о = т/2, рГ

+г(е + -^Ез -    + -W3 - г-Нз = ш/з, г        dr гг

—г(е Ч)/i Ч—/о = тЕ^ г г

—г(е Н)/2 — -pfo = пгЕ^, гdr

-г(е + -)/з + -/о = тЕ3, гг

+ 4h - г-h = тНх, dr г г

+i~(fi - /з) = тНз, Г

Ег(4" + -)/з + г-h = тН₃. (6) dr г г

Одновременно с операторами /2,/з будем диагонализировать оператор пространственной инверсии П. В представлении декартовой тетрады и декартова базиса матриц /3“ этот оператор имеет вид

П =

1 о о о

ООО

-Z 0   0   а

0 -Z о я

0   0 +Z

Р^(г) = Ф(-г).

Уравнение на собственные значения П'Ф = РФ дает два решения:

Р=(-1)^Я1, /о = /2 = 0, /з = -/1,

Ез = —Ех, Ез = 0, Из = Е1х

и р = И)ё h = h,

Ез = Ех, Нз = —Нх, Нз = 0.

Для состояний с Р = (—l)^j+1 имеем четыре уравнения:

+г(б + — )Ех + i(4" + ")^я1 + i-Нз = mfx, г        dr г        г

-г(еЕ-^х=тЕх, -г(4" +-)/1 = тНх, г                 dr г

^i-fx = тНз.                (9)

г

Для этого класса решений аномальный магнитный момент никак себя не проявляет в присутствии внешнего кулоновского поля. Система допускает полное решение для основной функции /f

/ d²    2 d , а. ₉     G + 1) А „

( "Т^ —3—Ь (е Ч )--2 ) /1 ⁼ 0- (Ю)

\ г dr        г        rz у

Это уравнение возникает в теории скалярной частицы во внешнем кулоновском поле, его точные решения и соответствующий спектр энергии известны.

Для состояний счетностью Р = (—1)^J имеем систему из шести уравнений:

-(4" + -)^Я2 - ^-Ех - 4h = mfo, dr г        г

+г(е 4— ^Ех + г(——|—= mfx, г        dr г

+г(е 4— )Ез — 2г—Pi-- ^"/о = ^mh^ гр             р         р ы

—г(е 4—)/₂ — ~j~h = тпЕз, г      dr

—г(е 4—)/i 4—/о = гпЕх, г       г

г(4" p4hPi-h =-тНх- (11) dr г г

2.    Случай минимального значения момента j = 0 3.    Нерелятивистское приближение, случай j = О

Для состояний с минимальным j = 0 нужно использовать более простую подстановку:

Фо = e-»£t/o(r), Ф = е"г£<

о

Ё = e"i£t

В₂(г) 0

Н = e"i£t

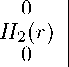
В этом случае получаем четыре радиальные уравнения:

9 Г dr г а Г

Л + -)Е2 - /о = т/2,

-г(е + -)/₂ - у/о = тЕ₂, Н₂ = 0.    (12)

г dr

Исключая Е₂, находим уравнения для функций

/о,/2:

. т² A a d ?Гт\

12 = i I (е Ч )-. у I Jo, Руг) \ г dr г² )

Р(г) = (б² — m²)r² + 2бат + а².

Исключая далее /2, получим уравнение 2-го порядка для функции / = /о

A f\

—У + [ —2жР-1+ I 2a2 х + 6Eax2 + 4Е2х3 )Р-2 + dx2 у           \/

+ ((2Е² - 2Р⁴)А + (4Еа - 6Е³а)ж⁴+

+ (2а² - 6Р²А)А - 2Еа³хЛр-А

/) dx

В системе уравнений (12) осуществим переход к нерелятивистскому приближению. Сначала исключим нединамическую переменную /о(г):

	г	z2 , d
,         х „ г(е Ч--)Е2 -	гаг2		-)e2 r
	1 d 1	4 , d
—г(е Ч--)/2 — т	m dr '	7A +	-W2 r

^/2 ) = mf₂, ^г Л _Р у В I — тЕ₂.

Затем вводим большие и малые компоненты [14] Ь = № + W), гЕ₂ = (В₂ ~ М₂\ Одновременно выделим энергию покоя формальной заменой с =^ т + Е, где А - нерелятивистская энергия. В результате получаем

(Е + -ЁВ₂ - М₂) - [г(у + -)(В₂ - М₂)-г           mr dr г

--2 (^2 + М2)] = 2шМ2,

(е + -хв₂ + м₂) - + -)№ - МЁ-г             т dr dr г

Д'

--2 № + М2)] = —2тМ₂.

Чтобы получить уравнение для большой компоненты В₂, сложим последние два уравнения и после этого малой компонентой М₂ в сравнении с большой В₂ можно пренебречь:

Г (d 2. Г\ „

2(Е Ч—)В2--у" (—।—)--j ) Л+ г      тг2 у dr г   г2 )

1 d / d 2   ?Г\ „

Ч--у ( 7--1---1--2 ) ®2 = 0.

т dr \dr г г2)

Отсюда находим (пусть В₂^Ё = В^^г^

гГ, d    2

г2 dr   г

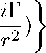
R(r) = 0.

Учитывая, что по физическим соображениям параметр Г чисто мнимый, сделаем замену гГ =^- Г:

+ [ж2Р | 2лАЕ | 72 —/от)/' 2Ч~ d2R 2 dR dr2 г dr

+ ((—2гР7 + 2гЕ37)ж3 + (—2г«7 + 4гР2а7)ж2 +

4-2гЕа2ух^Р 3)/ = 0, где используются безразмерные переменные ж, Е, у.

х = тт,  Е = —, 7 = тГ, а = --.

’ т '       ’        137

Полученное уравнение имеет сложный набор сингулярных точек. В следующем разделе выведем его нерелятивистский аналог, который будет существенно проще.

/        а    2   4 ГГ

+ 2т(Е+-)-у- — В = 0.(14)

\                 у^       гр ^      грОГ^ /

Уравнение (14) имеет две нерегулярные особые точки г = 0 и г = оо, обе ранга 2, оно относится к классу дважды вырожденного уравнения Гойна [15]. Локальные решения около точки г = 0 строим в виде

R=e^Arr^Be^f(rY           (15)

Для функции /(г) получаем уравнение

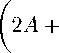
2В + 2 г

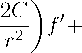
Л „  .2 2ЛВ + 2та + 2Л

+ 2тЕ + А Ч--

В² + В - 2АС - 2  —4Г - 2BG

Накладываем ограничения

2тВ + Л2 = 0, -Г2 + С2 = 0, 4Г + 2BG = 0, это дает

А = ±V-2mE (Е < 0), или в краткой форме

Рк-хСк-х + РкСк + РкрхСкрх = 0, где

Рк-х = а(к - 1) + bi, Рк = к(к - 1) + aifc + Ь₂,

Рк₊х = а2^к + 1).

Делим соотношение (20) на Ск-хк² и устремляем к к бесконечности: к —> оо

2Г

В = -— = ф2.

+ тт-а2(к+1)--= 0, hm ---= г.

к             Cfc Cfc-l к^оо Cfc-l

Для описания связанных состояний используем следующие значения:

Г > 0,

В = +2;

Г < 0, А = -V-2mE, С = +Г, В = -2. (16)

В результате получаем уравнение, определяющее радиус сходимости: значению г = 0 отвечает радиус Rcorw = pi = оо.

Приведем явный вид величин, задающих рекуррентные соотношения (формулы немного различаются для двух подслучаев):

С учетом (16) уравнение упрощается

Г +(2А+

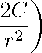
2АВ + 2та + 2А

В² + В- 2АС - 2

Г>0, P_k+x = W + ^

Рк-х = — 2\f—2тЁ (к — 1) — 6л/—2тЕ + Ima,

Рк = к(к — 1) + 6к + 4 — 2V~2mE Г, (21) Г < 0, Р_ки = -2Г(^+1),

Р_к-х = —2л/—2тЕ(к — 1) + 2\f—2тЁ + 2та,

Рк = к(к — 1) — 2к + 2V~2mE Г.     (22)

В качестве условия квантования используем условие трансцендентности функций Гойна [15]

Г > 0, Рк-х = —2V~2mE(k — 1)— —6V—2mE + 2та = 0,

Г < 0, Рк-х = —2У—2тЕ^к — 1)+

+2-\/—2m В + 2та

+2V—2тВ + 2та = 0.

2?У-2тЕ \. _ у

Оба эти уравнения можно представить символически так:

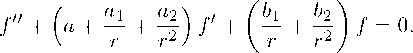
Отсюда находим две разные формулы для энергий в зависимости от знака Г:

Г >

0, Е = - — ’                2

(к + 2)2’

к >2,

Г<0-

к >2.     (23)

Решения уравнения (19) строим в виде степенных рядов с трехчленными рекуррентными соотношениями:

У(к - 1) + bi]c_fc_! + \к(к - 1) + ахк + Ь₂Ук+

Ц-а^к + l)cfc_|_i — 0               (20)

Формулы выглядят физически интерпретируемыми лишь частично, поскольку получаемые таким способом уровни энергии не зависят от параметра аномального момента Г. В то же время сами радиальные решения НУ) зависят от Г. Поэтому соотношения (23) едва ли описывают правильные спектры энергии.

4. Нерелятивистские уравнения, j = 1,2,...

v            гГ

Ч-2-(Ф! -фу¹) ч- ^2 (ф₂ ч- Ф2) =-2тфу,

Исходим из релятивистских радиальных уравнений:

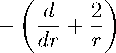
Ег

2-Еу--= т^0’

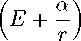
(Ф2 — -г/>2)

г т

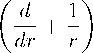
^у + чкН

+г ( 6 Ч--) Si + г — + - Ну = mfy, \    г)       \атг)

г (е + —) Е₂ - 2г—Ну -      = т/₂,

\       /            ТТ

. / ,d

6 + - /2 - у- /о = лгв₂, \ г) ат

V          J Г 1    .

+ -Ф2+^2     --г т            т2 т

- -^2)-

—2г-(Ф1 — -г/’г) Ч~ -у(Ф₂ Ч~ Ф2) =2тф2,

, а. . _т . d 1

Е+ - Ф₂ +V>₂ + --- т           ат т

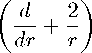
(ф₂ - чЬН

/    Q \       V

-г е + - /1 + -/о = тЕу, \     г)       Г

v            гГ

Ч-2-(Ф! - V>1) ч-^2 (ф2 ч--г/’г) =-2т-г/>2.

.( d   1А      V г у- + - J1 + г-h = -тНу.

\аг   т )      т

Исключим нединамические переменные fo,Hy.

Оставшиеся четыре уравнения примут вид

Чтобы получить нерелятивистские радиальные уравнения для больших компонент Ф1 и Ф2, складываем уравнения в каждой паре, и затем пренебрегаем малыми компонентами в сравнении с большими. В результате находим

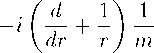
V d  1\    у

'У--'--) /1 + ^{г —}/2 \ аг   т )      т

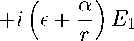
v 1

т m

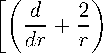
Е2 + 2—Еу + г

d2 2d dr2 r dr

d2 2d dr2 г dr

3-Xr 2z/²\

---2" Ф1“

2г + Гт

--у- Ф2

[З-Хт ^

= о,

2 4Г г2 «,3

г2А т

— ) Ф2-

—г ( 6 Ч— ) /1 = тЕу, \ г /

2r + Г

-2z/—— Ф1 = 0.           (25)

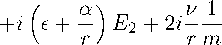
. f d 1\ , V "

г у + - /1 +г-Т +

\ аг т ) т

Поскольку Г чисто мнимый параметр, то в уравнениях сделана замена гГ на Г, а также использованы обозначения

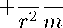
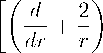
Е2 + ^Еу + ^/2

= т./2,

2тЕ = —А, А > 0, 2та = 3,

<1 1 dr m

d   2\       z/Г

3--1--I -^2 + 2 —£/i Чу/2

ат   т)        тт

-г ( 6 Ч-- ) /2 = тЕ^.

\ г /

Большие и малые компоненты вводятся соотношениями

/1 = (Ф1 + 7’1), гЕу = (Ф1 - -фу\

V =j(j + 1) = L.           (26)

Методом исключения можно получить уравнения 4-го порядка для каждой из функций Ф1(г) и Ф2(г). В частности, для функции Ф1 получаем уравнение d4 т    /    4      10\ d3 т

---Ф1 Ч----1-----Ф1Ч-dr4      \ 2г Ч- Г г у dr3

/2 = (Ф2 + ^2), гЕ2 = ^2 — ^-2)-      (24)

Тогда предыдущие уравнения дают (одновременно выделяем энергию покоя заменой е = т + Е)

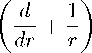
т

d 1Л /т , х у- + - Ф1 + ^1 + dr г /

+ ~(Ф₂ Ч~ ^2) + (е ч- —) (Фг - Ут) = 2тЗу, Т                 \ т)

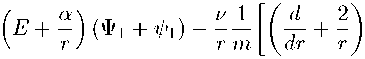
(ф₂ - з₂Н

48           8 A d2 т

Г(2г + Г) (2г + Г)2 7 dr2 1

/-8£ + 64-10Г²А-4Г/3 4L - 24 + 8Г/5

+                  +    р2 +

। 8 - 6£ 8Г 2Г2 ,

4Г2А + 16£-128 + 8Г/3      32 A dT

/ 2   16Г2А + 64Д + 32Г/3 — 2/ЗАГ3

у1

, — 10Г2А - 21Л - 12ГД + Д2Г2 + 2АДГ2 , р2г2

, 4Г2А + 4ГД + 8L- FVpL Г2Д , рг3

, -4ГД + £² + Г² А - 4L —32Г²А - 128Д - 64Г/3 ,

⁺       7^{4       +} Г^ТТТ) ⁺

-32Д - 8Г2А - 16ГДА т

Г2(2г + Г)2)

Символически структура уравнения записывается так (пусть Ф1 = F)

dr⁴ \ 2г + Г г / dr³

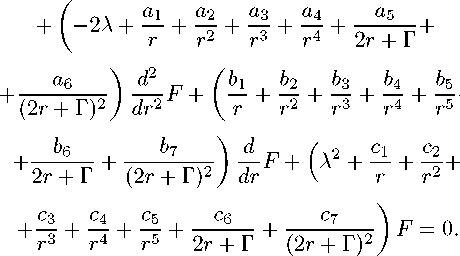
В окрестности регулярной особой точки г = —Г/2 это уравнение упрощается:

/ d⁴ 4 d³ ав d?

у dr⁴   2r + Г dr³   (2r + Г)² dr²

I 7 ^d , ^C7 A _{F = n} (2r + Г)² dr (2r + Г)² J "

Ищем его решения в виде F = (2г + Г)®. Для индекса s получаем при этом алгебраическое уравнение четвертой степени с простыми корнями:

Ф1 = (2г + Г)®, s = 0, -1, -3, -4 .   (27)

Только при s = 0 решения ведут себя в точке г = —Г/2 регулярно. Точка г = 0 является нерегулярной особой точкой и имеет ранг 2. Поэтому решения уравнения 4-го порядка в окрестности точки г = О ищем в виде

Ф^г) = e^Drr^Ae^B/4(7 •          (28)

Дальнейший анализ технически довольно громоздкий. Параметры D, А, В выбираются так, чтобы упростить вид уравнения для /(г). Приводим только конечный результат.

Существуют четыре различных решения:

(Г) D = -V^, В = О, Л = О,

F4=eD477(29)

• (II)    D = -V^, В = о, А = -1,

Fi = eDT-M-ry(30)

• (III)    D = -V^, в = +г, Л = -1,

F3 = еПт-е+г/Чз(тУ(31)

• (IV)    D =        В = -Г, А = +3,

F4 = e^^e^Ff^r).(32)

Решения для функций Л (г),/2 (г) строятся в виде степенных рядов с восьмичленными рекуррентными соотношениями. Решения для функций /зИ,/^) также строятся в виде степенных рядов, но с девятичленными рекуррентными соотношениями. Исследована сходимость этих четырех степенных рядов методом Пуанкаре-Перрона. Возможные радиусы сходимости следующие: Rcorw = |Г|/2, ос. Для описания связанных состояний можно использовать решения F₃, Г < 0 и F₄, Г > 0.

Условие трансцендентности решений здесь также дает формулу для энергий в виде Е = —const/n². Уровни энергии не зависят от параметра аномального магнитного момента. Последнее обстоятельство указывает на их непригодность для описания связанных состояний в системе.

Работа выполнена при финансовой поддержке гранта БРФФИ Ф19М-032 для молодых ученых и гранта БРФФИ Ф20РА-007 в рамках сотрудничества НАН Беларуси и Румынской Академии.