Частица со спином 1/2 и двумя массовыми параметрами во внешнем кулоновском поле

В работах [1–4] было предложено релятивистское уравнение для частицы со спином 1/2 и двумя массовыми параметрами. Показано, что в отсутствие внешних полей такое обобщенное уравнение для фермиона распадается на два обычных уравнения Дирака. В присутствии внешних электромагнит- ных полей происходит смешивание двух биспинор-ных компонент. Были построены точные решения такого уравнения в присутствии однородного магнитного поля.

Система уравнений для двух биспиноров Ф 1 ( x ) , Ф ₂ ( x ) в тетрадном формализме имеет структуру

^{Y ^{а [} i ( ^д а + ^Г а ) ^— eA a ^{] —} M 1 +

+ b A 1 S( x ) } Ф 1 ( x ) - aA 1 S(x )Ф ₂ ( x ) = 0 ,

^{{ y а [} i ^{( д} а ^{+ Г} а ) ^— eA a ^{] —} M 2 ^—

-a Л 2 S( x ) } Ф 2 ( x ) + b A 2 ^( x )Ф 1 ( x ) = 0;    (1)

Ya(x) = e^)Yb, S(x) = — ieFae''(x), ав( A    Yа (x)Yв (x) — Ye (x)Ya (x)

a x ) =

Используются следующие параметры:

M

.

⁴⁴1    (1 + cos y ) / 2 ,

M

M 1 = Ti--------Wo ’ Y ^ ^{[0 ,n/ 2]} , (1 — cos Y ) / 2

a = 2 M (^{4 —} 3 V^{1 + (1} / ^3)sin 2 Y ^{— cos} Y^ , b =2 MM (^4 ^{— 3}\A ^{+ (1} / ³⁾ sin ² y ^{+ cos} Y^ ,

Система уравнений (1) принимает вид

Y 0 ^ ^id t ^— r ) ⁺ iY 3 ^d r ⁺ r ^ 0ф ^— M 1 ⁺

+ iT ! Y ⁰ Y ³ Ф 1 — ^а 21 Y ⁰ Y ³ Ф 2 = 0 ,

Y 0 ( ^id t ) ⁺ iY 3 ^d r +—^ 9ф ^— M 2 ^— rr

• —iaY ⁰ Y ³ ] Ф 2 + i^ ² Y ⁰ Y ³ Ф 1 = 0 ,

где выделен зависящий от угловых переменных оператор

• s .» = iY 1 d . + Y ² i^d ± ±^{2a 1}L ^cos l • sin У

• Дальше будем учитывать явные выражения для четырех параметров:

a 1 = —

e 2      ^{(1 —} cos y ) _x

3 M cos y (1 + cos y )

( — cos y V 12 — 3cos ² y + cos ² y + 2)

3 M cos y (1 + cos y )         ’

_ 22 sin2 Y a a2  e 3 McosY,T 1

—

2 sin2 Y e 3 McosY < 0 ’

Л 1

( 1 + //1 + (1 /3) sin2 y^ x cos y — v/1 + (1 / 3)sin2 y x cos y (1 + cos y )

,

Л ₂

( 1 + //1 + (1 /3) sin2 y^ x cos Y +   1 + (1 / 3)sin2 y x--—--- cos y (1 — cos y )

.

Параметр M с размерностью обратной длины является произвольным.

1. Разделение переменных

Рассмотрим обобщенное уравнение в кулоновском поле:

A t = ^— r, F tr = ^—d r ^A 0 = ^— Г 2 ,

^{s( x} ) = ie 2 Y ⁰ Y 3 , применяем сокращающие запись обозначения a A i e ² = a 1 , a Л 2 e ² = a 2 , b A i e ² = в i , b A 2 e ² = в 2 •

e ² (1 + cos Y )

в 2 = — oTf----7n

3 M cos y (cos y — 1)

(cos y V 12 — 3cos ² y + cos ² y + 2)

X ------3M cos y (cos y — 1)

Отмечаем, что выполняются следующие соотношения между параметрами a2 = —в 1, a 1в2 = —в2 •

Подстановка для волновой функции с квантовыми числами ϵ, j, m имеет вид

-iϵt

Ф 1 ( x ) = ----

_e -iϵt

Ф 2 ( x ) = ----

f 1 ( r ) D - 1 / 2 f 2 ( r ) D +1 / 2 f 3 ( r ) D - 1 / 2 f 4 ( r ) D +1 / 2

g 1 ⁽ r ) D - 1 / 2 g 2 ( r ) D +1 / 2 g 3 ( r ) D - 1 / 2 g 4 ( r ) D +1 / 2

Используется аппарат D -функций Вигнера. С учетом матриц Дирака в спинорном представлении получаем восемь радиальных уравнений:

—

r

d i   f3

dr

—

—

i^νf 4

r

—

m 1 f 1 + irl ¹ f 1

—

iα 1

r 2 g 1     ⁰ ,

α dν ϵ + r ) f4 + idrf4 + irf3- - M1f2 - -2f f2 + iα1 "T2" g 2 = 0 ’ α dν ϵ + r ) f1 + id^f1 + i^f2 - iβ1      iα1 - M16f 2 —-2- f 3 + -2- g 3 = 0, α dν ϵ + r f2 - i dr f2 - i r f1 - - M1f 4 + -Г2- f 4 - iα1 Г 2 g 4    0, α dν ϵ + r g3 - i dr g3 - i r g4 - iα2 - m2 g 1 - -^2- g 1 + '-el f1 = 0. α dν ϵ + r ) g 4 + id^g4 + i rg 3 - iα2 - M2 g 2 + -^2- g 2 - ie2 f2 = 0. α dν ϵ + r ' g 1+id^g 1+i^g 2 - iα2 - M2 g 3 + ^2- g 3 - ie2 6f2 = 0, α dν ϵ + r g2 - idrg2 - irg1- iα2 - M2 g 4 - -^2- g4 + ie2 f4 = 0, (3) где v = j + 1 /2; j = 1 /2,3/2,... Система (3) допускает наложение условий, вытекающих из требования диагонализации оператора пространственной четности:

f 3 = 6f 2 , f 4 = 6f 1 ,6 = ± 1 ,

g = ( g 2 + g 1 ) , G = i ( g 2 - g 1 );

в результате получаем

d dr	ν - r		β 1 + 6~ 2 -	F-
				α 6 + - r		- δM 1	f-δαr 2 1 G	= 0 ,
d dr	+	ν r	β 1 - δ r 2	) f +
			+	6 +	α r	+ 6M 1'	) f + 60 1 g	= 0 ,
d dr	-	ν r	α 2 - δ r 2	) G-
			-	6 +	α r	- δM 2	) g + 6в f	= 0 ,
d dr	+	ν r	α 2 + 6—2	g +
			+	6 +	α r	+ 6M 2	G-δ β r 2 2 f	= 0 .

g з = 6g 2 . g 4 = 6g 1 , ⁶ = ± 1;

Удобно рассматривать состояния с разной четностью по отдельности:

6 — +1 ,		в 1 A r 2 e 1 a r 2 a 2 A r 2	F- f + ( G-	α r		M 1 M 1 M 2	f- F + g +	0 1 g = 0 ,
d -dr d I "T" + dr d -dr	ν - + r ν - r ν - r
				6 + 6 +	α + r α - r			α 1 r 2 g = в | F =	0 , 0 ,
/ d dr	ν + - r	α 2 + r 2 +	g + 6 +	α --+ M 2 r		) G -	- ; 1 f = 0;		(5)

	α	dν
6 + rf 1 + id-f 1 + 'г J 2 - -    M 1 6f 2 - ie 1 f 2 + iO L 6g 2 = 0 , ’ a ) , .d       v 6 + rf 2 - id-f 2 - 'г f 1 - -    M 1 6f 1 + ie 1 6f 1 - iO- 6g 1 = 0 , α  dν 6 + r)g 1 + id^g 1 + i^g 2 - -    M 2 6g 2 + Г 22Г 6g 2 - -Г 22 6f 2 = 0 2 α  dν 6 + rg g 2 - id-g 2 - i^g 1 - - m 2 6g 1 - iaa 2 6g 1 + irb- 6f 1 =0 . Вместо f 1 и f 2 используем комбинации этих

f = ( f 2 + f 1 ) , F = i ( f 2 - f 1 );

⁶ = ^{- 1} .

dν dr r

- e1) F - ( ^e + ^a + M 1 ) f + Э G = ⁰ ,

d ν dr r

в 1 ) f +

(⁶ + ° - m 1) f -a g = 0 ,

функций:

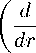
ν

r

+ 0 2) G - ( 6 + ^a + M 2 ) g - ^F = 0 , r ²                r               r ²

dν dr r

-

+

α

6 + - r

\ _ DO

- M 2) G + ^ f = 0 .

Эти две системы уравнений связаны формальным преобразованием

M 1 , M 2 , α 1 , α 2 , β 1 , β 2 ⇒ -M 1 , -M 2 , -α 1 , -α 2 , -β 1 , -β 2 .

Если рассматривать эти уравнения при достаточно больших r , то пренебрегая слагаемыми, содержащи-

ми r

-

² , приходим к двум несвязанным подсистемам

Выразим из второго и четвертого уравнений функции F, G и подставим в первое и третье уравнения. В результате получаем два уравнения второго порядка

уравнений для двух обычных дираковских частиц с массами M ₁ и M ₂ во внешнем кулоновском поле. Это означает, что достаточно далеко от центра r = 0 будем наблюдать две несвязанные между собой частицы с различающимися массами.

d ² f

dr +

' 2 M 1 a

-

r

^v ( ^{v +} 1) , r 2    ⁺

^{2 e} i ( ^v + 1)

r ³

-

2. Нерелятивистское приближение

Чтобы упростить задачу, перейдем к нерелятивистскому приближению. Исходим из уравнений (5), (6). Вводим две нерелятивистские энергии E 1 и E ₂ : б = M 1 + E 1 , б = M ₂ + E ₂ ; при этом уравнения примут вид

-

-

β 1 ²    M 1 α 1 β 2

r 4 ⁺ MO5^ ^{+ 2 M 1 E 1}

α 1 r ²

-

α 1 M 1 dg να 1 r ² M ₂ dr     r ³

M 1 α 1 ν

M ₂ Г ^{3 +}

α 1 β 1    α 1 α 2 M 1

r ⁴

-

M 2 r ⁴

f +

-

2 a 1 r ³

-

g = 0 ,

8 — +1 , d

-

dr

-

v ₊ в 1

r r ²

^f + Э G = 0 ’

_d 2 _g

—- + dr ²

2 M 1 a

-

v ( v + 1)   2 a 2 ( v + 1)

-

r

r ²

-

r ³

-

-

d ν dr r

-

- 2 ) f— (2 m 1 + e 1 + a

α ₁

^— r 2 g = ⁰ ,

^a 2    M 2 ^a 1 ^в 2     ^ ^ ^

r4 + M^ + 2M2E2] g+

-

-

+

-

d

ν

dr

-

-

r

^α 2             ^α

—2 J G + ^ E 2 +—

-

^ F = 0 ,

β 2

r 2 ⁺

в 2 M 2 A df ₊ v-h ₊ 2 - 2 ₊ r ² M ₁ dr     r ³     r ³

d ν dr r

α 2

+ r2

2 M 2 + E 2 + “

r

§ f = 0;

₊ M 2 в 2 v

⁺ M 1 r ³

+

α ₂ β ₂    β ₁ β ₂ M ₂

r ⁴

-

M 1 r ⁴

f = 0 .

⁸ = ^{— 1} , d

ν

-

dr

-

-

-

-

r

d

\T" +

dr

d

dr

-

-

Эти уравнения (учитываем (2))

симметричны относительно замен

β α r 1 ) F + (^2 M 1 + E 1 + -

α ₁

2 G = 0 ,

f ^ g, a 1 ^ -в 2 , a 2 ^ -в 1 , M 1 ^ M 2 ;

ν

r

β 1

⁺ r 2

r

α r2 g = 0,

следовательно, достаточно исследовать уравнение четвертого порядка только для одной функции. Приведем общую структуру уравнений (7) и (8):

^v + “2) G + 2² M ² + E 2 + “ r r ²                       r

§ F = 0 ,

dr2 + b+ 7+ r2 + rt+ r4

dν dr r

-

-

r

r

в 2 f = 0 .

+

c d c 3 c 4

—— ⁺ — ⁺ r 4

r ² dr

r

g = 0 ,

Рассмотрим сначала уравнения при 8 = +1 . Пренебрежем энергией в сравнении с массой покоя

d 2 + в +- dr ²          r

B 2

⁺ r 2

B 3   B 4

⁺ r 3 ⁺ r 4

α

2 M 1 + E 1 +—

r

к 2 M 1 2 M 2 + E 2 + - к 2 M 2 , r

/ C d r2 dr

C 3   C 4

r 3 ⁺ r 4) g ⁰ .

тогда получим

Для случая с противоположной четностью

( 8 = — 1) получаем уравнения

8 — +1 ,

d

-

dr

-

ν

+

r

β 1 r ²

d2F dr2 +

2 M a

—— +

r

-

d

"T" ⁺ dr

ν

-

-

dν

-

dr r

d

-

r

-

α 2 r ²

v ( —v + 1)

r ²

+

^{2 в} 1 ⁽ -^{v +} 1)

r ³

-

F + ( E 1 + |)f + | 1 G = 0 ,

в ! ) f — 2 M 1 F — “ 1 g = 0 ,

β 2

g^— r 2 ^F = ⁰ ,

-+ ^v + ^ 2

dr r   r ²

g — 2 M 2 G + в| f = 0 .

Mαβ ^MNr 2 ⁺ 2 M 1 E 1

F +

-

' + r ⁴

+

α 1	α 1 M 1	dG + dr	να 1	2 a 1
r 2	r 2 M 2		r 3	r 3

+

-

M 2 r ⁴

r ⁴

α ₁ β ₁    α ₁ α ₂ M ₁

M 1 α 1 ν

M 2 Г ³

G = 0 ,    (9)

d2G dr2 +

2 M 2 a

-

r

^{v ( v —} !) , r 2    ⁺

2 a 2 ( v — 1) r ³

-

α ²₂    M 2 α 1 β 2

Г 4 ⁺ M 1 г ⁴

+ 2 M 2 E 2

G +

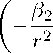
β 2 M 2 r ² M 1

dF

"T" ⁺ dr

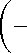
ve 2 ₊2 в 2 r ³ r ³

-

M 2 в 2 v ₊ a 2 в 2 _ в 1 в 2 M 2 A F = ₀

M ₁ r ³      r ⁴      M ₁ r ⁴

Уравнения (9),(10) отличаются от (7),(8) только формальными заменами

III, IV. C + 0 , A = _v,v + 1 .     (15)

Будем следить за случаями, пригодными для описания связанных состояний: т. е. I и IV при положительных A. Дальше приходим к уравнению со сложной структурой, его решения строятся в виде степенных ∞ рядов G(г) = У^ dkrk с 10-членными рекуррентными соотношениkя=м0и

f ⇒ F, g ⇒ G, ν ⇒ -ν.        (11)

Приведем общую структуру уравнения четвертого порядка для функции g :

d ⁴ g ₊ / m 1 ₊ dr ⁴       r

m 2 г ³ + m 2 г ² + m 4 г + m 5

P

+

+

n 1    n 2    n 3    n 4

n ^{0 +} Г ⁺ Г 2 ⁺ r 3 ⁺ Г ^{4 +}

П 5 Г ³ + П 6 Г ² + П 7 Г + П 8

P

+

Q k- 9 d k- 9 ⁺ Q k- 8 d k- 8 ⁺ • • • ⁺ Q k d k = ⁰ . ⁽¹⁶⁾

Условие получения трансцендентных решений

Q k- 9 = 0 , ^ ^ 10 ( k _ 9) + L 9 = 0 ,k _ 9 = П >  0 , при A = v + 2 , B = —V— 2 M 1 E 1 имеет вид

8[( _ 5 + v + k )p _ 2 E 1 M 1 _ aM 1 ] ■ ( M 1 _ M 2 ) ² M 2 ( _E 2 M 2 + E 1 M 1 ) E 1 = 0 ,

откуда следует

₌ 1      a ² M 1

¹      2[ k - 7+( v + 2)] ² .

p 1 p 2 p 3 p 4

_Г ⁺ _Г 2 ⁺ _Г 3 ⁺ _Г 4 ⁺

Пусть B = _^— 2 M ₂ E ₂ , тогда получаем

+

P 5 Г 3 + p 6 Г ² + p 7 Г + p 8 A dg + dr

P

₌ 1      a ² M ₂

² = 2[ k - 9+( v + 2)] ² .

q 1

q о + r +

q 2 q 3     q 4

_Г 2 _Г 3 ⁺ _Г 4 ⁺

q 5     q 6     q 7

Г 5 + Г 6 + Г 7 + q8

r 8 ⁺

q 9 Г ³ + q 10 г ² + q 11 г + q 12

+

P g = 0,

где P обозначает полином четвертого порядка:

P = 2 E 1 M 2 ( M 1 _ M 2 ) ² г ⁴ + 2 M 2 a ( M 1 _ M ₂ ) ² г 3 + +2 M 2 ( v + 1)[(2 v + 1) M 2 + M 1 ] г 2 + +2 M 2 ( v + 1)[( _ 3 в 1 + a 2 ) M 2 + M 1 ( в 1 + a 2 )] г + ^{+ [ в} 2 ^a 1 ^{+ 2 в} 1 ^{( _a} 2 ^{+ в} 1 ^{)] M} 2 ^_

—M 2 M 1 ( —a 2 + в 2 + 2 в 2 a 1 ) + M 2 a 1 в 2 •

Выполнив подстановку g = e ^Br g ( г ) , находим четыре возможных значения для B :

B = _p- 2 M 1 E 1 , + V _ 2 M 1 E 1 ,

_ p _ 2 M 2 E 2 , + p _ 2 M 2 E 2 . (12)

Далее выполним подстановку g = r ^A e ^C/r G ( г ) , для определения параметра C получаем уравнение четвертого порядка C ⁴ +(2 a 1 в 2 _в 2 _a 2 ) C ² + ( —а 1 в 2 + a ₂ в 1 ) ² = 0; отсюда, учитывая соотношение (2), получаем

C ⁴ _ 4 C ² в 2 = 0 ^ C = 0 , 0 , ± 2 в 1 .

Возможны следующие варианты:

• I.    C =+2 в 1 <  0 , A = v + 2 >  0;     (13)

• II.    C = _ 2 в 1 >  0 , A = -< <  0;     (14)

Выбрав параметры A, C , согласно (15), и проделав аналогичные вычисления, получим еще два выражения для спектров:

A = v + 1 , B = _ y _ 2 M 1 E 1 ,

1 a ² M 1

¹ = 2 [ k - 6+( v + 1)] ² ’ ⁽¹⁹⁾

A = v + 1 , B = _ y _ 2 M 2 E 2 , 1      M a ²

E 2 = 2[ k_ 8+w< . ⁽²⁰⁾

С точностью до переобозначения параметров имеем только два разных спектра.

Для состояний с противоположной четностью получаем спектры (используем формальные замены v + 2 ^ v, v + 1 ^ v )

A = ^v,B = ^_ P- ² M ¹ E ¹ , E ¹ = ^_ |[ k “7^v ] 2 , A = ^v,B = ^_ P- ^{2 M} 2 ^{E 2} , ^{E 2} = ^_ |[ k “Mv ] 2 ’ A = ^v,B = ^_ P- ^{2 M 1 E 1} , ^{E 1} = ^_ |[ k “ 6 M + ¹ v ] 2 , A = ^v,B = ^_ P- ^{2 M 2 E 2} , ^{E 2} = ^_ 2[ k ^M8 2 + v ] 2 .

Здесь также с точностью до переобозначения параметров имеем два разных спектра; причем они совпадают с предыдущими.

Остановимся на структуре нерелятивистских волновых функций. В нерелятивистском описании имеем следующие приближенные равенства:

5 = +1 , f 1 = f + iF к f, f 2 = f - iF к f, g i = g + iG к g, g 2 = g - iG к g ; (21)

5 = - 1 , f 1 = f + iF к iF, f 2 = f — iF к -iF, g 1 = g + iG к iG, g 2 = g - iG к -iG. (22)

Соответственно, нерелятивистские 2-компонентные волновые функции имеют вид

5 = +1 , Ф 5 ₌₊i =

f ( r ) D - 1 / 2

f ( r ) D +i / 2

g ( r ) D — 1 / -2

g ⁽ r ) D +1 / 2

5 = - 1 , Ф 5 =+1 = i

F ( r ) D - 1 / 2

-F ( r ) D ₊₁ / ₂

+ i

G ( r ) D - 1 / 2

G ( r ) D +1 / 2

Заключение

Обобщенное уравнение для фермиона с двумя массовыми параметрами исследовано в случае присутствия внешнего кулоновского поля. Показано, что вдали от кулоновского центра система представляется как простая совокупность двух несвязанных частиц дираковского типа с фиксированными разными массами. Однако при рассмотрении системы во всей области изменения радиальной переменной две компоненты сложной системы связаны объединенной системой уравнений и не могут рассматриваться как независимые. Удивительным представляется тот факт, что анализ сложной системы радиальных уравнений во всей области изменения переменной, тем не менее, приводит в нерелятивистском описании к тем же двум выражениям для энергий, как если бы две компоненты с разными массами были независимыми. Установление этого спектра основывается на использовании условия трансцендент- ности для решений фробениусового типа результирующих уравнений четвертого порядка. По-видимо-му, большего понимания поведения частицы со спином 1 /2 и двумя массовыми параметрами можно достичь, если построить решения радиальных уравнений в релятивистском случае, не используя перехода к нерелятивистскому приближению.

Работа выполнена при финансовой поддержке МО РБ по договору № 1410/2021.