Частотная стабилизация однофотонного источника на основе спонтанного параметрического рассеяния света с помощью внешнего электрического поля

Разработка источников однофотонных состояний электромагнитного поля является актуальной задачей современной квантовой оптики и квантовой информатики (см. обзоры [1 – 4]). Очевидным подходом к решению данной задачи является использование спонтанного излучения одиночной квантовой системы (молекулы, квантовой точки, холодного атома, центра окраски в алмазе и т.п.). Достоинствами такого источника являются отсутствие вклада многофотонных состояний и детерминированность. Кроме того, при использовании микрорезонаторов можно получить высокую эффективность генерации в заданную пространственную моду. Однако такие источники, как правило, позволяют генерировать спектрально ограниченные однофотонные импульсы, соответствующие чистым квантовым состояниям, лишь при низких температурах. Кроме того, однофотонные импульсы получаются в виде затухающей экспоненты, что неудобно для практического использования. Альтернативным и широко используемым методом генерации однофотонных состояний является процесс спонтанного параметрического рассеяния света (СПР) в нелинейных средах, в ходе которого рождаются коррелированные пары фотонов, один из которых детектируется. Достоинствами источников на основе СПР являются возможность перестройки в широком диапазоне длин волн, а также возможность создания чистых однофотонных состояний и управления их временной формой при комнатной температуре. Для ряда задач квантовой оптики необходимо создавать источники однофотонных состояний, эффективно взаимодействующие с резонансными системами атомов, спектр поглощения которых составляет от единиц до сотен МГц. Если спектр бифотонного поля необходимо подстраивать под линию поглощения, то существенным становится влияние внешних условий на генерацию однофотонных состояний: температурные условия, стабильность лазера накачки и т.п. В связи с этим становится актуальным вопрос о методах стабилизации однофотонных источников на основе СПР.

В данной работе обсуждается возможность стабилизации узкополосного однофотонного источника на основе противонаправленного СПР с помощью внешнего однородного электрического поля за счёт линейного электрооптического эффекта Поккельса. Противонаправленный вариант СПР, когда коррелированные фотоны испускаются в противоположные стороны по отношению к волновому вектору излучения накачки, позволяет генерировать узкополосные однофотонные состояния с высокой степенью чистоты [5–8] и представляет интерес для создания безре-зонаторных узкополосных однофотонных источников. Возможности управления спектром СПР за счёт внешнего электрического поля исследовались только для обычного (сонаправленного) варианта СПР в работах [9, 10].

Спонтанное параметрическое рассеяние света

Спонтанное параметрическое рассеяние света – процесс распада фотона накачки на два фотона сигнального и холостого поля в квадратично нелинейной среде. При этом должны выполняться условия частотного и пространственного синхронизмов:

ω _p =ω _s +ω _i ,                                 (1)

k_p = k_i + k_s ± 2 π / Λ ,                               (2)

где ω p , ω s , ω i , k p , k s , k i – частоты и волновые векторы накачки сигнального фотона и холостого фотона соответственно ( k m = ω m n ( ω m )/ c , m = i , s , p ), Λ – период доменной структуры нелинейного кристалла, n – показатель преломления. Использование периодически модулированных сред позволяет получить режимы генерации, которые недоступны при обычных условиях синхронизма, в частности противонаправленный режим генерации СПР, когда сигнальный и холостой фотоны испускаются в противоположные стороны по отношению к волновому вектору излучения накачки.

Вектор состояния поля коллинеарного СПР можно записать в виде (см., например, [11]):

I Ψ ) = 0 ) + ∫∫ d ω _i d ω _sF ( ω _i , ω _s ) I ω _i )l ω _s ) ,            (3)

где F (ω i , ω s ) – спектральная амплитуда бифотона, которая определяет спектральные и пространственные свойства рассеянного поля. В случае коллинеарного режима генерации амплитуда бифотона:

| F ( to , ., to , )| ² = A² | h ( A kL )| ² , (4) где A – константа взаимодействия, h ( x ) = e^-ix/2 sinc( x/2 ), Δ k – расстройка волновых векторов вдоль оси распространения z . Для кристаллов с периодической модуляцией нелинейности расстройка волновых векторов определяется следующим образом [5, 6]: а) Δ k = k p + k i – k s – 2π m /Λ для противонаправленного режима; б) Δ k = k p – k i – k s – 2π m /Λ для сонаправленно-го режима.

Электрооптический эффект

Электрооптический эффект заключается в изменении значения показателя преломления под действием электрического поля. Под линейным электрооптическим эффектом Поккельса подразумевается квазилинейная зависимость показателя преломления от напряжённости электрического поля [12].

В анизотропных средах значения показателя преломления зависят от направления распространения электромагнитной волны в среде. Распределение показателей преломления удобно описывать в виде поверхностей Френеля:

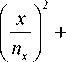
X n y J

y

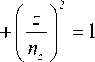
где x , y , z – кристаллооптические оси, n i – значение показателей преломления вдоль кристаллооптических осей. Под действием внешнего однородного электрического поля E = ( E x , E y , E z ) происходит модификация поверхности Френеля:

a xx x ^{2 +} a yy y ^{2 +} a zz z ^{2 + 2} a xy xy ^{+ 2} a zx zx ^{+ 2} a yz yz = 1, ⁽⁶⁾

где a ij = 1/ n ij + Σ r ijk E k ( i , j , k = x , y , z ), r ijk – линейные электрооптические коэффициенты ( n ii = n_i ² _i ). В зависимости от типа симметрии кристалла некоторые электрооптические коэффициенты оказываются нулевые. Принято переобозначать: xx = 1, yy = 2, zz = 3, xy = 4, zx = 5, yz = 6. Таким образом, трёхмерная матрица [ r ijk ] 3×3×3 сводится к двумерной матрице [ r hk ] 6×3.

Управление спектром спонтанного параметрического рассеяния света

Управление спектром СПР возможно за счёт изменения показателей преломления нелинейного кристалла с помощью внешнего электрического поля. В работах [9, 10] было показано, что за счёт приложения неоднородного поля к кристаллу можно не только уширить спектр, но также создать дополнительные условия генерации, которые не свойственны кристаллу без электрического поля. Основные спектральные свойства бифотонного поля определяются амплитудой бифотона (4).

В случае, когда на нелинейный кристалл действует электрическое поле E , волновой вектор принимает вид:

^k m ( ^E ) = ^{2 П} n ( ^ m , ^E ) / ^ m , ^ m = ^{2 П} c / ® m .          ⁽⁷⁾

Таким образом, волновой вектор фотона будет зависеть от электрического поля, приложенного к нелинейному кристаллу, следовательно, амплитуда бифотона (4) приобретёт зависимость от E :

I F ( E , to i , to , )| ² =| A² | h ( a k ( E ) L )| ²                      (8)

Чтобы более точно проанализировать зависимость спектра СПР от электрического поля, рассмотрим периодически модулированный кристалл титанил-фос-фата калия (KTP). Электрооптические коэффициенты для кристалла KTP [6] приведены в табл. 1. Если рассмотреть действие однородного электрического поля вдоль осей кристалла KTP, то эллипсоид Френеля модифицируется следующим образом:

Г           "'

I I + - +1- I + 2 Ъ Exxz = 1,(9)

I n J       Пл, I

X x /    \ y /x у л2 га2 (Л

-- I ⁺ --- ⁺ I I ^{+ 2} r 42 E y yz = 1, n x J   X n y )   X n z )

A

-1 ⁺ r 13 ^Ez n x ²

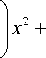
⁽ 1

— ⁺ r 23 ^Ez X ny

y2 +1 4 + Г33Ez\ z2 = 1,(11) X nz

J

где i = 1, 2, 3 ( x , y , z ).

Табл. 1. Электрооптические коэффициенты для кристалла титанил-фосфата калия [6]

Электрооптические коэффициенты	Значение, пм/В
r 13	9,5
r 23	15,7
r 33	36,3
r 51	7,3
r 42	9,3

В случае, когда внешнее электрическое поле имеет все три компоненты E = ( E x , E y , E_z ), происходит поворот и растяжение (сжатие) эллипсоида Френеля, причём угол поворота эллипсоида будет определяться амплитудой внешнего электрического поля. В случае, когда внешнее электрическое поле направлено вдоль оси z E = (0,0, E_z ), происходит лишь растяжение (сжатие) эллипсоида Френеля (соотношение (11)), что приводит только к сдвигу частоты генерации бифо-тонного поля. Далее предполагаем, что однородное электрическое поле действует вдоль оси z (выражение (11)), так как в этом случае не происходит изменение исходного режима генерации спонтанного параметрического рассеяния света.

Для численного расчёта рассматривался периодически модулированный кристалл KTP с периодом модуляции Λ = 2,03 мкм [8]. Данный период модуляции нелинейности позволяет реализовать противонаправленный режим СПР для случая, когда длины волн поля накачки, сигнального и холостого фотонов равны 532 нм, 810 нм и 1550 нм соответственно.

Используя соотношение (11), получаем, что волновые векторы фотонов будут определяться формулой:

k i ( E ) = ^n^E) ,                       (12)

A i

где

- 1/2

n i ( E_z ) = 1 ' + r i з E_z I                                   (13)

I П J значение показателя преломления в присутствии внешнего однородного электрического поля.

Для численного моделирования смещения спектра СПР использовались 4 типа синхронизма: а) тип 0 – сигнальный и холостой фотон поляризованы параллельно накачке; б) тип I – сигнальный и холостой фотон поляризованы перпендикулярно накачке; в) тип IIа – сигнальный и холостой поляризованы перпендикулярно друг другу, сигнальный – параллельно накачке; г) тип IIб – сигнальный и холостой поляризованы перпендикулярно друг другу, холостой – параллельно накачке. Значения показателей преломления без учёта электрического поля вычислялись с помощью формул Сельмейера [14].

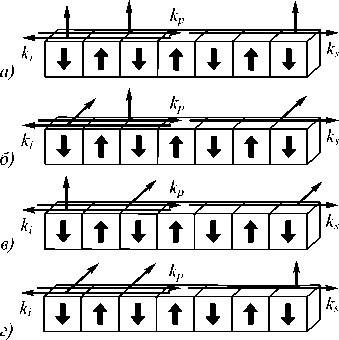
Рис. 1. Направления распространения и направления поляризации излучения накачки, сигнального и холостого фотонов относительно кристалла KTP при различных типах синхронизма: а) синхронизм типа 0; б) синхронизм типа I; в) синхронизм типа IIа; г) синхронизм типа IIб. Поперечные стрелки указывают направление поляризации света, стрелки внутри кристалла, вырезанного вдоль оси x, показывают направление оси z внутри доменов

Результаты численного моделирования показывают (рис. 2), что сдвиг спектра параметрического рассеяния является линейным относительно внешнего однородного электрического поля, причём наибольшая чувствительность к внешнему электрическому полю (Δν sh ≈ 1,7 МГц/(В/см)) достигается в случае синхронизма типа I. Таким образом, изменение внешнего поля в пределах ±100 В/см обеспечивает перестройку частоты испускаемых фотонов в диапазоне 340 МГц. Этого вполне достаточно для стабилизации однофотонного источника при отсутствии соответствующей стабилизации лазера накачки.

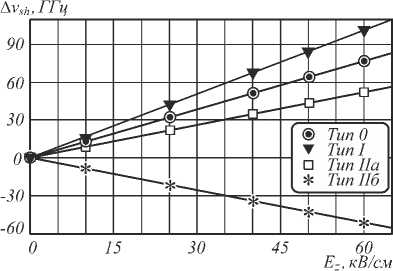
Рис. 2. Сдвиг спектра холостых фотонов ∆ν sh = ν i (E z )–ν i (0) как функция внешнего электрического поля для различных типов синхронизма противонаправленного режима СПР

Заключение

Произведён расчёт зависимости спектра СПР в нелинейном кристалле с периодической доменной структурой от величины внешнего однородного электрического поля. Рассмотрены варианты противонаправленного режима СПР в периодически модулированном кристалле KTP, и определён тип синхронизма, обладающий наибольшей чувствительностью к внешнему полю. Данные результаты могут быть использованы для частотной перестройки и стабилизации однофотонных источников на основе СПР.

Работа выполнена при поддержке Российского научного фонда (грант № 14-12-00806).