Четырёхволновое взаимодействие на тепловой нелинейности при больших коэффициентах отражения c учётом самодифракции волн накачки

Несмотря на многолетние исследования многоволновых преобразователей излучения, обращающих волновой фронт (ОВФ) падающей волны в реальном масштабе времени, большой круг вопросов, связанных с анализом качества ОВФ такими преобразователями излучения, остаётся открытым. В частности, до настоящего времени анализ соответствия между комплексными амплитудами падающей (сигнальной) и «обращённой» (объектной) волн проводился, как правило, в приближении малого коэффициента отражения [1, 2]. Однако уже выполнены эксперименты, в которых достигнут коэффициент отражения порядка и больше единицы [3,4]. Поэтому актуальным является изучение качества ОВФ при больших коэффициентах отражения. В этом случае, наряду с динамической решёткой, образованной при интерференции сигнальной волны с первой волной накачки, необходимо учитывать наличие в нелинейной среде ещё одной динамической решётки, образованной при интерференции объектной волны и второй волны накачки.

1. Вывод основных уравнений

Пусть в среде с тепловой нелинейностью, расположенной между плоскостями z = 0 и z = I , распространяются навстречу друг другу две волны накачки с комплексными амплитудами A ₁ и A ₂ и сигнальная волна с амплитудой A ₃ . В результате вырожденного четырёхволнового взаимодействия to+to-to=to генерируется объектная волна с амплитудой A ₄ . Стационарное волновое уравнение, описывающее такое взаимодействие, есть

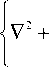
k ² 1 1 +—— 8 T I - 2 ik a

V n ₀ d T   J

г x

( xl E Aj- +

V j = 1

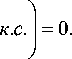
Здесь n0 – среднее значение показателя преломления, k = ton0 Cc - волновое число, a - коэффициент по глощения, 8T - изменение температуры, обусловленное выделением тепла при поглощении излучения.

Уравнение (1) необходимо дополнить уравнением Пуассона

V ² 8 T i ^{a Л} c p v

E A j + к . с . = 0 , j = 1

где Л - температуропроводность, c p - удельная теплоёмкость, v - объёмная плотность вещества.

Изменение температуры представим в виде суммы быстро меняющихся ( 8 T ₃₁ , 8 T ₄₂ ) и неменяю-щейся ( 8 T 0 ) в зависимости от поперечной координаты ( р ) составляющих

8 T ( р , z ) = 8 T o ( z ) + 8 T 31 ( р , z ) + 8 T 1 ( р , z ) +

+8 T 42 ( P , z ) + 8 T 4 * 2 ( P , z ).

Составляющие изменения температуры 8 T ₀ , 8 T ₃₁ и 8 T ₄₂ удовлетворяют уравнениям

+ -^( A 4 + A A) = 0,

dz    Л cp vx            '

V ² 8 T ₃₁ +-^a- A A ' = 0,                     (4)

• ³¹ Л c p v ^{1 3}

• V28 T42 +-a- A2 a; = 0.

^Л c p ^v

При условии неизменности температуры на гранях нелинейной среды граничные условия на изменения температуры запишутся в виде

8 T ,( z = 0) = 8 T 0 ( z = I ) = 0,

8 T 31 ( z = 0) = 8 T 31 ( z = I ) = 0,                      (5)

8 T ;2 ( z = 0) = 8 T ;2 ( z = I ) = 0.

В приближении заданного поля по волнам накачки (| A _1j2| >>| A ₃,₄| ), из (1) с учётом (3) уравнения, описывающие изменение комплексных амплитуд волн накачки, сигнальной и объектной волн, имеют вид

Jv 2 + I	k 2 ( 1 +——8 T 1 - 2 ik a _ V n 0 d T 0)        _	| A . = 0, m = 1,2,
Jv 2 +	, (     2 dn | k 2 1 +-- 8 T - 2 ik a	> A 3 +
I	IV n 0 d T 0 J     J	I
2 k 2	dn _      _ .
+	-- ( 8 T 42 + 8 T * ) A = 0,	(6)
n 0	d T 42      31 1
Jv 2 +	(    2 dn | k 2 1 +-- 8 T - 2 ik a
I	IV n 0 d T 0 J J	I 4

A 4 = A ₄ exp { -a ( z -I ) - iC ( z ) + iC ( I ) } ,

A ’ = A₃ exp { a z + iC ( z ) } .

Уравнения, описывающие изменение составляющих температуры по толщине нелинейного слоя, перепишутся следующим образом

• ^d 2^{8 T} 31   v²S.T f        ^J ■ ^к2

• —Пк8 T31 =- f A3 exp 0- iz - 2az dz|

• d28T42    2^ г V*    J . к2    -

• —к8 T42 =- f, A4 exp 0 i—z + 2az ^ dz|

+ 2k- —(8 T, +8 T* ) A = 0.

31       42    2

n ₀ d T

Пусть волны накачки плоские и распространяются строго вдоль оси Z : A 1 = A 1₀ ( z )exp ( - ikz ) , A = A 20 ( z )exp ( ikz ) . При выполнении граничных условий A ₁₀ ( z = 0) = A ,, A 20 ( z = I ) = . 1 . в приближении медленно меняющихся амплитуд из (6) изменение амплитуд волн накачки по толщине нелинейной среды есть

^A 10 ^{( z} ) = ^A 00 exp [ ^{- iC ( z} ) ^{- a z} ] ,

A 20 ( z ) = A 200 exp [ i [ С ( z ) - С ( I ) ] + a ( z -1 ) ] .

Здесь f l = —" A ⁰ , f , = —" A 200 exp { - 2 al } .

у^л c p          у^л c p

При выводе уравнений (9), (10) считали, что к = к3 = к4T = -к4 = -к3T , к = | к|.

Уравнения для амплитуд сигнальной и объектной волн должны быть дополнены граничными условиями

A ‘ ( к , z = 0) = А 3^ ( к ), А 4 ( -к , z = I ) = 0.       (11)

Здесь C ^{( z} ) = — dn j⁸ T 0 ^{( z} i )d z 1 .

n ₀ d T ₀

Разложим амплитуды сигнальной и объектной волн по плоским волнам

Дважды продифференцировав уравнения (9) с учётом (10), получим систему из двух связанных дифференциальных уравнений для пространственных спектров объектной и сигнальной волн

d ³ A ‘ к ² d ² A ‘

—У + i--У

d z ³ k d z ²

к2 +

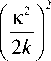
dA 3

d z

^

^A p ^{( P} , ^z ) = J ^A p ^{( K} p , ^{z )e}xP { ^- i ^K p P ^{- ik} pz z } ^{d K} p ,   (7)

- iG 1 A 3 exp ( - 2 a z ) = iGA 4* exp [ 2 a ( z -1 ) ] ,

p = 3,4.

Здесь к р и k_pz - поперечная и продольная составляющие волнового вектора k_p , — pp | = k .

Изменения температуры разложим по гармоническим решёткам

d A ₄     . к ² d A ₄      2 ( к ² | dA ₄

3+12к + I I

d z ³      k d z ²          V 2 k ) d z

^

8 T gi ( P , z ) = J 8 T ^x T 3 , z )exp { - i к 3 t p } d K 3 t ,

-^

^

- iG ₂ A , exp [ 2 a ( z -1 ) ] = iGA 3 exp ( - 2 a z ) .

Здесь G 1,2 = -dn -^( A O20 ) 2 , G ² = G 1 G 2 .

’    n0 dT Л cp v x ’ 2

Наряду с граничными условиями (11), система уравнений (12) должна быть дополнена граничными условиями

8 T 42 ( P , z ) = J 8 TT 42 ( K T 4 , z )exp { - i к 4 t P } d K 4 T . -^

С учётом (7), (8) в параксиальном приближении

dA 3

z = 0

d A ’

z =1

= 0, d A ⁴

d A 4

z = 0

= 0, (13)

z =1

k pz = ^k V

_

p 2 |i

У

уравнения, описывающие изменения

пространственных спектров сигнальной и объектной волн, примут вид

‘

-y¹ = ^- ig 1 ^[8 T 2 ^{+ 8} T * ^{] x} exp 0 dz ^{L J} [

^

774- = ig 2 ^[8 T 1 ^{+ 8} T O ^{] x} exp 0 i dz ^{L J} I

■ к² 1

- i— z k

2 k I

к ²

z 2 k

.

k d n          k d n

Здесь g 1 = — — ^A 10 , g 2 = — — A 0 , n ₀ d T          n ₀ d T

вытекающими из неизменности температуры на гранях нелинейного слоя.

Если в качестве сигнальной волны рассматривается сигнал от точечного источника, расположенного на передней грани нелинейного слоя, то A ₃3₀ ( к ) = 1.

При отсутствии последних слагаемых в левых частях системы уравнений (12) эти уравнения описывают четырёхволновое взаимодействие при больших коэффициентах отражения без учёта само-дифракции волн накачки. При отсутствии в первом уравнении слагаемого iG 1 A , exp [ - 2 a z ] , а во втором уравнении - слагаемого iG ₂ A 4 * exp [ 2 a ( z -1 ) 1 сис-

тема уравнений описывает четырёхволновое взаимодействие при малом коэффициенте отражения с учётом самодифракции первой волны накачки.

2.    Обсуждение результатов

Система уравнений (12) с учётом граничных условий (11), (13) анализировалась численными методами. На рис. 1, 2 приведены зависимости от параметра G‘ = G11 амплитудного коэффициента отра- жения объектной волны

A 4 ( к = 0, z = 0 )

A’(к = 0, z = 0)

и

амплитудного коэффициента преобразования сиг- нальной волны

K =

A (к = 0, z = i) A3 (к = 0, z = 0)

при различ-

ных соотношениях между интенсивностями волн

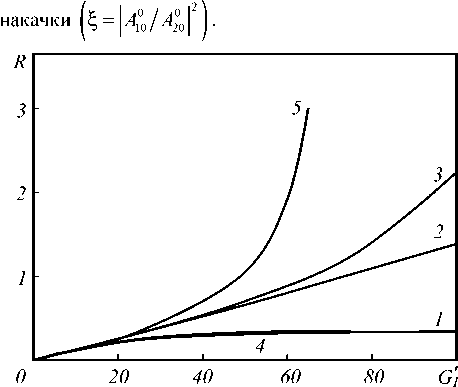
Рис. 1. Зависимость коэффициента отражения от интенсивности волн накачки при al = 1; 2k l = 10 ;

§ = 0,3( 1), 0,75( 2), 1( 3), 3( 4) ,1 (5, без учёта

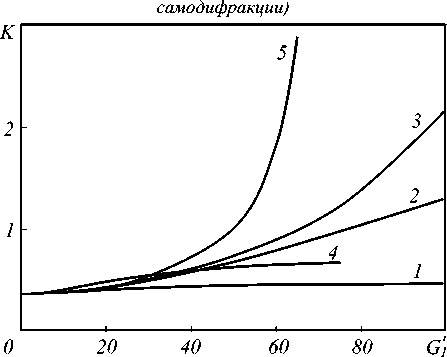
Рис. 2. Зависимость коэффициента преобразования сигнальной волны от интенсивности волн накачки при al = 1; 2kl = 10; § = 0,3(1), 0,75(2), 1(3), 3(4),

1 (5, без учёта самодифракции )

Для сравнения на этих же графиках приведены зависимости коэффициентов R и K при ^ = 1 от интенсивности волн накачки без учёта их самоди-фракции (рис. 1, 2, кривые 5). Увеличение интенсивности волн накачки приводит к монотонному увеличению коэффициентов отражения объектной волны и преобразования сигнальной волны. Причём максимальный рост коэффициентов R и K с увеличением параметра G1 наблюдается при равных интенсивностях волн накачки. С ростом разности между интенсивностями волн накачки скорость изменения коэффициентов R и K с увеличением интенсивности волн накачки уменьшается.

Без учёта самодифракции увеличение интенсивности волн накачки приводит к более резкому изменению коэффициентов отражения объектной волны и преобразования сигнальной волны.

На рис. 3 приведены характерные графики изменения модулей пространственных спектров объектной и сигнальной волн по мере их распространения в нелинейной среде.

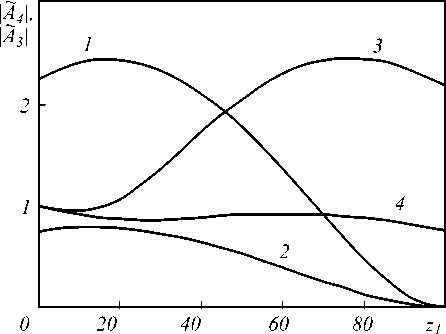
Рис. 3. Изменения модулей пространственных спектров объектной (1, 2) и сигнальной (3, 4) волн при al = 1;

2k l = 10 ; G' , = 100 , К1 2k = 10~³ (1, 3) ;

3,2 ■ 10 - 2 (2, 4)

При малом коэффициенте отражения четырёхволнового преобразователя излучения ( R « 1) по мере распространения в нелинейной среде на нулевой пространственной частоте амплитуда пространственного спектра сигнальной волны монотонно уменьшается, а амплитуда спектра объектной волны монотонно увеличивается. С ростом коэффициента отражения скорость изменения амплитуды пространственного спектра сигнальной волны падает, а скорость изменения амплитуды спектра объектной волны растёт.

Если коэффициент отражения больше единицы, то по мере распространения в нелинейной среде амплитуды пространственных спектров сигнальной и объектной волн вначале возрастают, а затем уменьшаются. Причём области нелинейной среды, в пределах которых |.А 4 ( к = 0, z 1 )| и I A 3 ’ ( к = 0, z 2 )| принимают наибольшие значения, пространственно разделены (рис. 3).

При фиксированном коэффициенте отражения, большим единицы, с ростом пространственной частоты скорость изменения амплитуды пространственного спектра объектной волны по мере её распространения в нелинейной среде уменьшается, амплитуда пространственного спектра сигнальной волны вначале возрастает, а затем уменьшается.

Анализ пространственного спектра объектной волны на передней грани нелинейного слоя показывает, что с ростом пространственной частоты модуль пространственного спектра либо монотонно уменьшается, либо вначале возрастает, а затем уменьшается. Для характеристики пространственной селективности четырёхволнового преобразователя при условии монотонного уменьшения с ростом пространственной частоты пространственного спектра объектной волны введём полуширину полосы пространственных частот Ак , определяемую из выражения

I A 4 ( к = Ак , z =

0)| = 2|A4 (к = 0, z = 0)| .

Нормированная полуширина полосы пространственных частот ( Ак₁ = Ак^I/ 2 k ) без учёта само-дифракции волн накачки с ростом их интенсивности при ^ = 1 монотонно уменьшается (рис. 4, кривая 5).

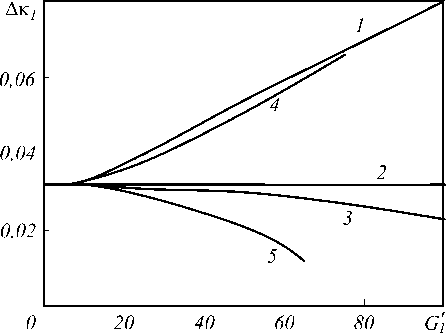
Рис. 4. Зависимость полуширины полосы пространственных частот от интенсивности волн накачки при al = 1;

2k l = 10 ; § = 0,3( 1), 0,75( 2), 1(3), 3( 4 ) ,1(5, без учёта самодифракции )

При малом коэффициенте отражения и с учётом самодифракции только первой волны накачки (^ » 1) рост интенсивности волн накачки увеличивает полосу ширины пространственных частот. Таким образом, процессы самодифракции волн накачки и перекачки энергии из сигнальной волны в объектную и наоборот взаимно исключающе влияют на полуширину полосы пространственных частот. При Aio = Ao большее влияние интенсивности волн накачки на изменение полуширины полосы пространственных частот связано с процессами перекачки энергии из сигнальной волны в объектную и наоборот, поэтому рост интенсивности волн накачки приводит к уменьшению полосы пространственных частот (рис. 4, кривая 3). По мере увеличения отклонения интенсивности первой волны накачки от интенсивности второй волны влияние процессов са-модифракции на изменение полуширины полосы пространственных частот возрастает, что приводит к росту величины Ак1 с увеличением интенсивности волн накачки (рис. 4, кривые 2, 3, 4).

Изменение фазы объектной волны (ф) на полу ширине полосы пространственных частот

(Аф=ф(к = 0, z = 0)-ф(к = Ак, z = 0))

с ростом интенсивности волн накачки минимально при равных интенсивностях волн накачки (рис. 5, кривая 3). По мере увеличения отклонения интенсивности первой волны накачки от интенсивности второй волны изменение фазы объектной волны на полуширине полосы пространственных частот с ростом интенсивности волн накачки монотонно рас-

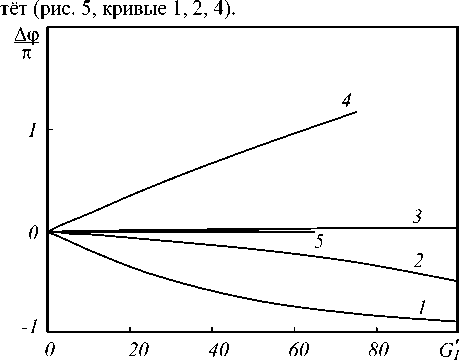
Рис. 5. Изменение фазы на полуширине полосы пространственных частот при al = 1; 2k l = 10 ;

§ = 0,3(1), 0,75(2), 1(3), 3(4) 1(5, без учёта самодифракции )

В качестве примера рассмотрим ОВФ излучения с длиной волны 10,6 мкм в нелинейной среде CCℓ4 , для которой а = 18 см-1,   — = 5,4-10-4 град-1, dT n0 = 1,46, Лcpv = 1,03-10-3 Дж/(см-страд) [5]. Будем считать, что интенсивности волн накачки одинаковы. При толщине нелинейного слоя I = 1 а полуширина полосы пространственных частот при малом коэффициенте отражения Ак - 57 см-1. При коэффициенте отражения R = 2 (параметр G’ = 95,5 ), что соответствует интенсивности волн накачки 9,3 Вт/см2, полуширина полосы пространственных частот уменьшается до значения равного Ак - 42 см-1.

Заключение

1. Учёт самодифракции волн накачки, перекачки энергии из сигнальной волны в объектную и наоборот оказывает существенное влияние на коэффициент отражения, пространственную селективность четырёхволнового преобразователя излучения на тепловой нелинейности. При равных интенсивностях волн накачки значительное уменьшение ширины полосы пространственных частот четырёхволнового преобразователя излучения с ростом интенсивности волн накачки наблюдается при коэффициенте отражения, большим единицы.

2. По мере увеличения разности между интенсивностями волн накачки эффект их самодифракции начинает оказывать на величину полуширины полосы пространственных частот большее влияние, чем перекачка энергии из сигнальной волны в объектную и наоборот. Это приводит к росту полосы пространственных частот четырёхволнового преобразователя излучения с увеличением интенсивности волн накачки.

Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры России» на 2009-2013 годы (Государственный контракт 3. № 14.740.11.0063).