Четырёхволновое взаимодействие на тепловой нелинейности в схеме с положительной обратной связью

Эффективность четырёхволновых преобразователей излучения ю 1 + ю 2 - ю 3 = ю 4 в средах с различным типом нелинейности (керровская, резонансная, тепловая) определяется, как правило, произведением интенсивностей волн накачки на длину взаимодействия, на величину нелинейной восприимчивости среды [1–2]. Переход к средам с резонансной нелинейностью позволяет путём подбора частот взаимодействующих волн значительно повысить значение нелинейной восприимчивости [3–7]. Увеличение интенсивности с одновременным увеличением длины взаимодействия можно реализовать при четырёхволновом взаимодействии в волноводах [8–12].

Ещё один способ повышения эффективности многоволновых преобразователей заключается в наложении положительной обратной связи либо на волны накачки, либо на объектную и сигнальную волны. Использование интерферометра Фабри – Перо для реализации обратной связи на волны накачки позволяет значительно увеличить дифракционную эффективность четырёхволнового преобразователя излучения в средах с резонансной и тепловой нелинейностями [13]. Для четырёхволнового преобразователя на керровской нелинейности наложение положительной обратной связи на объектную и сигнальную волны путём помещения нелинейной среды в кольцевой резонатор на порядки повышает коэффициент отражения таких преобразователей [14–15].

Представляет интерес изучение влияния обратной связи, осуществляемой как по сигнальной, так и по объектной волне, на коэффициент отражения четырёхволнового преобразователя излучения на других типах нелинейности, в частности, на тепловой нелинейности.

страняются навстречу друг другу две волны накачки с комплексными амплитудами A 1 и A 2 и сигнальная волна с амплитудой A 3 . В результате вырожденного четырёхволнового взаимодействия ю + ю - ю = ю генерируется объектная волна с амплитудой A 4 .

Уравнение Гельмгольца, описывающее такое взаимодействие, есть

')- 2 ik а .( A + A *) = 0.   (1)

V² + к² 1 1 + —— 5 T I n ₀ d T

Здесь A = ^ A j , n ₀ - среднее значение показателя j = 1

преломления среды, к =( ю n ₀)/ c - волновое число, а -коэффициент поглощения, 5 T - изменение температуры, обусловленное выделением тепла при поглощении излучения.

Уравнение (1) необходимо дополнить уравнением Пуассона

V25T + -aI- = 0, Л cp v

где I = AA * - интенсивность излучения, Л - коэффициент теплопроводности, c_p – удельная теплоёмкость, v - объёмная плотность вещества.

Выражение для интенсивности излучения можно записать следующим образом i = 10+A1 a; + a; a3+A a4* + A2: a4.               (3)

Здесь 1 ₀ = A 1 a ; + A 2 A 2^: .

Тогда изменение температуры можно представить в виде суммы быстро (δ T 31 , δ T 42 ) и медленно (δ T 0 ) меняющихся в зависимости от поперечных координат составляющих

5 T ( r ) = 5 T 0 ( _z ) + 5 T 31 ( p , _z ) + 5 T 42 ( p , _z ) + + 5 T 3KP , _z ) + 5 T 42 ( p , _z ).

Пусть волны накачки плоские

/^

—*

A 1,2⁽ r ) = A 1,2⁽ z ^)exP^{( - ik} i2 r ).

Сигнальную и объектную волны разложим по плоским волнам

да

A j ( r ) = J A ( к , z ) exp( — i j — i — ) d^-,

—да

——

j = 3,4.

Здесь A j ( к _у ., z ) - пространственный спектр j- волны,

— —

p - поперечная составляющая радиус-вектора r , к j и k jz – поперечная и продольная составляющие волнового вектора k j , | k j | = к .

Изменения температуры разложим по гармоническим решёткам да

8 T 3i ( P , z ) = J 8 7 31 ( к т 3 , z )exp { — i к т 3 P } d K т 3 ,

волн накачки строго вдоль оси Z : к 1 = к ₂ = 0, к _{т 3} = —к ₃, к _{т 4} = —к ₄, к = к ₄ = —к ₃, к = | к |. Эта система уравнений должна быть дополнена граничными условиями на пространственные спектры сигнальной и объектной волн, на пространственные спектры температурных решёток.

При расположении четырёхволнового преобразователя внутри кольцевого резонатора (рис. 1) граничные условия на пространственные спектры сигнальной и объектной волн есть

^A ' ( к , z = 0) = TA — r f - A зo ( K ) +

—да да

8 T 42 ( p , Z ) = J 8 T 4 ₂( K T 4 , z )exp { — i K T 4 ^p} d ^K T 4 ,

—да

^         -^

где 8 T ₃₁, 8 T ₄₂ - пространственные спектры температурных решёток.

С учётом (5)–(7) из уравнений Гельмгольца и Пуассона в приближении заданного поля по волнам накачки (| A 1,2 | >> | A 3,4 |) получим систему связанных дифференциальных уравнений, описывающих изменение по толщине нелинейного слоя пространственных спектров сигнальной и объектной волн

d A 3

= — i ^—dnA [8 T 42 + 8 7 3 ; ] exp n ₀ d T

— 1

к2

2 k

d A 4

^{k d n} y0 X-T* J ^к2 I — A 2 0 [^{8 T} 31 ^{+8 T} 42 ] exp 1 i^^z 3 , n ₀ d T ^{L J} [ 2 к

температурных решёток [16]

d² 8 T₃₁ d z ²

к28 T31 =

aA,0A'*      f .к2     „ 1

-------exp <— i — z — 2 a z 3 , рЛ c p     [ 2 к

d² 8 T 42 d z ²

к28 T42 =

a A0 A '* f к2                 1

^CM2^{0 4} exp <  i — z + 2 a ( z — / ) 3 .

рЛ cp      ( 2 к

Здесь

A ( к ₄, z ) = ^( к ₄, z )exp { —a ( z — / ) — iC ( z ) + iC ( / ) } ,

-A 3 ( к 3 , z ) = A ( к 3 , z ) exp { a z + iC ( z ) } , A ° = . A , ( z = 0),

A 20 = -A 2 ( z = / ); C ( z ) = — dn fs T )( z i )d z , - фазовый n ₀ d T ₀

набег, обусловленный самовоздействием волн накачки.

Система уравнений (8)–(9) записана в параксиальном приближении, при условии распространения

x exp {—a/ — iC (/)} A3 (K, z = /),~ *        --- Г        к2 )

A ‘ ( к , z = 0) J^r exp — ikL + i— L x 4'         ¹² 4       2 к J

x exp {—a/ — iC (/)} = A4 (K, z = /), ^

где A ₃₀( к ) - пространственный спектр сигнальной волны в плоскости z =0 при отсутствии кольцевого резонатора, r 1 – коэффициент отражения полупрозрачного зеркала связи, r 2 – коэффициент отражения сферических зеркал резонатора, осуществляющих перенос пространственного распределения поля с одной плоскости нелинейного слоя ( z =0) на плоскость, расположенную на расстоянии L от другой плоскости ( z = ℓ ).

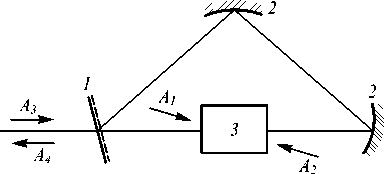
Рис. 1. Схема четырёхволнового взаимодействия в кольцевом резонаторе: 1 – полупрозрачное зеркало, 2 – сферические зеркала, 3 – нелинейная среда

Как показано в [2], при равных интенсивностях волн накачки

C ro=—— An     x

n0 dT 4aЛcpv

x {(a) 1(1 — exp (—2a/)) — / [1 + exp (—2a/)]}.

Граничные условия на спектры температурных решёток запишем из условия неизменности температуры на гранях нелинейного слоя

8 T31 (к T3, z = 0) = 8 T31 (к T3, z = /) = 0,8 T42 (к T 4, z = 0) = 8 T42 (к T 4, z = /) = 0.

2. Четырёхволновое взаимодействие при малом коэффициенте отражения

Будем рассматривать четырёхволновое взаимодействие при малом коэффициенте отражения, без

учёта самодифракции волн накачки. Тогда система уравнений (8) примет вид

dA; о, dz dA4    к к dn о I. к

---= i--A ,,o T . exp< i — z d z    n ₀ d T 2 ^{00 1}     [ 2 к

n2_rr г -к d n  a / о V

Здесь G   ^G 1 G 2 , ^G 1,2                ( A 120 ) ,

•     n ₀ d T Л c_p v ^x ' '

.

Из (13) следует, что A ’ ( к , z ) = const. Используя граничное условие на пространственный спектр сигнальной волны (10), найдём

A ’ ( к , z ) = V1 - rA зо ( к ) x

К2                 / x^

- ikL + i— L -a £ - iC ( £ )

2 к             ^V ')

.

Зная пространственный спектр сигнальной волны, из (9) найдём пространственный спектр температурной решётки

™ - a      a A- 0 A f

5 T . ( к , z ) =------------— x

' Л C p v ( p ² -к ²)

x

2 sh^ { e^xP⁽ -к z ) [ e^xp⁽ к ^{£ )} - exp⁽ -P ^{£ )} ] } +

^{+ 1}    { exp( ^к z ) [ exp( ^-P ^£ ) ^- exp( ^-K ^£ ) ] }

2 sh ( к £ )¹                                    '

-     1

exp( P z )

Здесь p = 2 a + i к ² /(2 к ).

-

Подставив выражение для пространственного спектра температурной решётки (15) в уравнение для пространственного спектра объектной волны (13), проинтегрировав правую и левую части уравнения по координате z с учётом граничного условия (10), получим выражение для пространственного спектра объектной волны на передней грани нелинейного слоя вида

■14 ( к , z = 0) = 2 GT ( 1 - p )^- ( в ² - к ² ) ^{- 1} x

x

к   )у i — + к I sh(к£)

2 к     )I

x< [ exp( -p £ ) - exp( -^

1 +

+

У к ²    )

I i --к I sh( к £ )

I 2 к )

у-1

x

P = r f rye exp

. , x                 к ²

-a £ - iC ( £ ) - ikL + i—L .

^{v !}         2 к

Из выражения (16) следует, что при условии сопряжения передней и задней граней нелинейного слоя ( L =0) наличие обратной связи не влияет на пространственную селективность четырёхволнового преобразователя излучения. С ростом пространственной частоты амплитуда пространственного спектра монотонно уменьшается.

Найдём наибольшее значение пространственного спектра объектной волны

A 4 ( к^ 0, z = 0) =

iGJA;*

———³--- x

^{8 a} ( 1 ^- P 0 )

x[ ( a ) ¹ [ 1 - exp( - 2 a £ ) ] - £ [ 1 + exp( - 2 a £ ) ] ] .

Здесь p ₀ = p ( к^ 0 ) = УУ" exp [-a £ - iC ( £ ) - ikL ] .

Тогда с учётом (14) выражение для амплитудного коэффициента отражения четырёхволнового преобразователя излучения запишется следующим образом

R =

X A ₄ ( к^ 0, z

= ⁰ )

A *

A 30

GУ 1 - Г exp ( -a £ )

^{8 a 2} ( 1 ^- p 0 ) ( 1 ^- p 0 )      (18)

x|^ ( a ) ¹ [ 1 - exp( - 2 a £ ) ] - £ [ 1 + exp( - 2 a £ ) ] J .

Отличие в коэффициенте отражения при наличии и отсутствии кольцевого резонатора есть

^ =

R ( r * 0 )

R ( Г 1 = 0 )

= ^1 - r x

rr2      2 Jriry cos [ kL + C (£)J exp (2a£)         exp (a£)

I                         Г к x 4 [exp(K£) - exp(-P£)] 1 - exp I i 2^

-к I £

1+

( 1 - exp ( - 2 a £ ) ) a

.

На рис. 2 приведены графики зависимости коэффициента отражения четырёхволнового преобразователя излучения от коэффициента отражения полупрозрачного зеркала. При условии cos [ kL + C ( ℓ )] = 1 с увеличением r ₁ коэффициент отражения четырёхволнового преобразователя излучения вначале возрастает, достигает максимального значения, а затем уменьшается до нуля (рис. 2, кривые 1, 2). Существуют области значений аргумента функции cos [ kL + C ( ℓ )], при которых наличие кольцевого резонатора приводит к «проигрышу» в коэффициенте отражения четырёхволнового преобразователя излучения (рис. 2, кривая 4).

При фиксированном значении коэффициента r2 и cos [kL + C(ℓ)] = 1 существует оптимальное значение коэффициента отражения полупрозрачного зеркала r1 opt=(4 r2 )-1exp (2a£)[ y+^rrexpi-2»^)-1],

при котором «выигрыш» в коэффициенте отражения четырёхволнового преобразователя излучения за счёт использования кольцевого резонатора максимален и равен

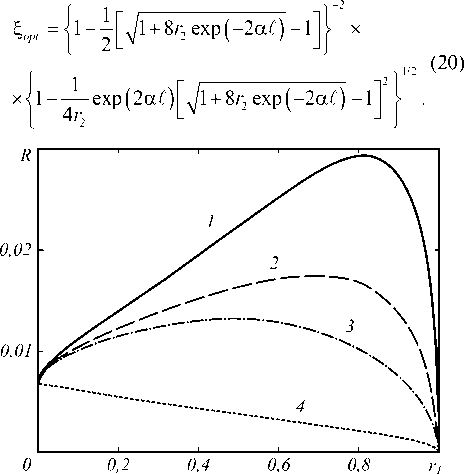
Рис. 2. Зависимость коэффициента отражения четырёхволнового преобразователя излучения от коэффициента отражения полупрозрачного зеркала при kl = 5 - 10 3 , a l = 10^-1, G = 10^-1, kL + C(l) = 0 (1,2), n /6 (3), n /2 (4), Г 2 = 0,7 (1, 3 ,4), 0,5 (2)

Наибольшее значение ^ opt наблюдается при a l ^ 0

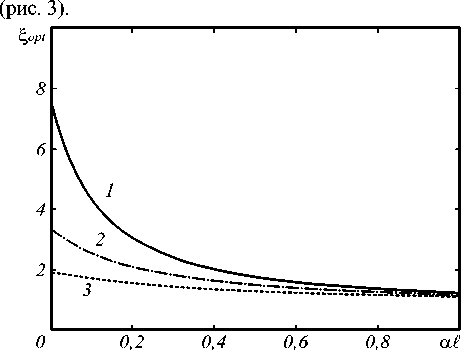
Рис. 3. Зависимость оптимального «выигрыша» от коэффициента поглощения при kl = 5 - 10 3 , cos [kL + C(ℓ)] = 1, r 2 = 0,7 (1), 0,5 (2), 0,3 (3)

Уменьшение значения функции cos [ kL + C ( ℓ )] с ростом аргумента, обусловленное либо самовоздей-ствием волн накачки, либо увеличением расстояния L , приводит к монотонному уменьшению оптимального значения коэффициента отражения зеркала связи, уменьшению параметра ^ opt .

3. Четырёхволновое взаимодействие при большом коэффициенте отражения

При учёте двух температурных решёток 5 T 31 и 5 T ₄₂, самодифракции волн накачки на этих решётках,

из системы уравнений (8)–(9) получим систему из двух связанных дифференциальных уравнений третьего порядка для комплексных амплитуд объектной и сигнальной волн

d³ A 3 . к ² d² A 3      2 [к ² | dA 3

---;—+ i--z К +    dz3     k dz2          I 2 kJ dz

- iG 1 A exp ( - 2 a z ) = iGA ’ exp |^2 a ( z - I ) ] ,

d³ A 4 ‘ . К² d²<      2 ( к ² ) d3L ‘

+ iк +1 I dz3     k dz2         (2 k J   dz

- iG ₂ vi‘* exp [ 2 a ( z - £ ) ] = iGA 3 exp ( - 2 a z ) .

Наряду с граничными условиями (10), система уравнений (21) должна быть дополнена граничными условиями

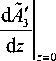
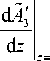
= 0,

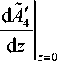
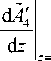
вытекающими из условия неизменности температуры на гранях нелинейной среды.

Система уравнений (21) с учётом граничных условий (10), (22) анализировалась численными методами. Расчёт коэффициента отражения четырёхволнового преобразователя излучения на тепловой нелинейности проводился на основе многократного прохождения сигнальной и объектной волн кольцевого резонатора, содержащего нелинейный слой, в котором распространяются две волны накачки. При этом граничные условия для нахождения комплексных амплитуд сигнальной и объектной волн при последующих их проходах через кольцевой резонатор определялись значениями комплексных амплитуд этих волн на гранях нелинейного слоя при предыдущих проходах. Ошибка расчёта коэффициента отражения четырёхволнового преобразователя излучения не превышала 0,2%.

На рис. 4 и 5 для случая A ”0 = A ₂⁰₀ приведены зависимости амплитудных коэффициентов отражения от нормированной интенсивности волн накачки

L £ d n ( A w)² )

G0 =---^     n0 dT Лcp v j при условии сопряжения передней и задней граней нелинейного слоя (L =0) (рис. 4) и при условии компенсации фазового набега, возникающего вследствие самовоздействия волн накачки путём подбора расстояния L (kL + C(l)=2nm, m = 0,±1,±2,...) (рис. 5). Для сравнения на этих же графиках штриховыми линиями изображены зависимости коэффициентов отражения от нормированной интенсивности волн накачки, полученные с использованием выражения (18).

При сопряжении кольцевым резонатором граней нелинейного слоя увеличение интенсивности волн накачки приводит вначале к росту, затем к уменьшению, а потом вновь к увеличению коэффициента от-

ражения. Существует область интенсивностей волн накачки, в пределах которой наложение обратной связи на объектную и сигнальную волны путём помещения четырёхволнового преобразователя в кольцевой резонатор не увеличивает эффективность таких преобразователей.

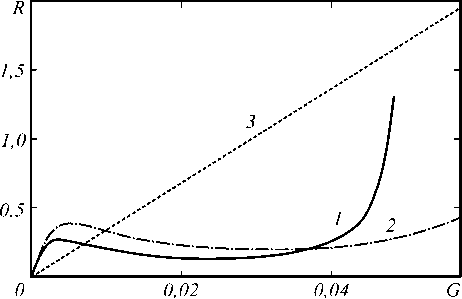
Рис. 4. Зависимость коэффициента отражения от интенсивности волн накачки при сопряжении кольцевым резонатором граней нелинейного слоя при kℓ = 5 ⋅ 10 ³, α ℓ = 10 ^–1, r 1 = 0,8 (1, 2), r 2 = 0,7 (1, 2), r 1 = r 2 = 0 (3)

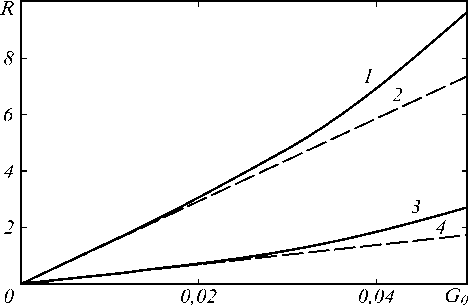
Рис. 5. Зависимость коэффициента отражения от интенсивности волн накачки с учётом компенсации фазового набега при kℓ = 5 ⋅ 10 ³, α ℓ = 10 ^–1, r₁ = 0,8 (1, 2), r 2 = 0,7 (1, 2), r 1 = r 2 = 0 (3, 4)

С физической точки зрения характер зависимости коэффициента отражения от нормированной интенсивности волн накачки вытекает из граничных условий (10). С ростом интенсивности волн накачки увеличивается фазовый набег (C(ℓ)), что приводит вначале к рассогласованию сигнальной волны на передней грани нелинейного слоя, состоящей из двух волн, одна из которых падает на эту грань нелинейной среды извне, а другая с помощью кольцевого резонатора «перебрасывается» с задней грани нелинейного слоя на переднюю. Уменьшается как амплитуда сигнальной волны, так и амплитуда объектной волны. При дальнейшем увеличении интенсивности волн накачки сигнальные волны, падающие на переднюю грань нелинейной среды извне и «перебрасываемые» с помощью кольцевого резонатора с задней грани нелинейного слоя на переднюю грань, оказываются сфазиро- ванными. Увеличивается амплитуда сигнальной волны, а значит, и амплитуда объектной волны.

Следует заметить, что при сопряжении кольцевым резонатором граней нелинейного слоя, несмотря на качественное совпадение характера зависимостей коэффициентов отражения от интенсивности волн накачки, полученных как с использованием аналитического выражения (18), так и численным методом, количественное совпадение результатов наблюдается лишь для малых интенсивностей волн накачки ( G 0 ≤ 0,001). Это связано, прежде всего, с неучётом при выводе выражения (18) самодифракции первой волны накачки. С увеличением интенсивности волн накачки возрастает амплитуда волны, возникающей при самодифракции первой волны накачки на температурной решетке δ T 31 , что приводит к дополнительному увеличению амплитуды сигнальной волны на задней грани нелинейного слоя и, соответственно, при C ( ℓ ) <  π – к уменьшению, а при C ( ℓ ) >  π – увеличению амплитуды сигнальной волны на передней грани нелинейного слоя. Это, в свою очередь, уменьшает или увеличивает амплитуду объектной волны.

При условии компенсации фазового набега, возникающего вследствие самовоздействия волн накачки либо путём смещения нелинейного слоя вдоль оси резонатора, либо введением в резонатор одного или нескольких оптических модуляторов, позволяющих управляемо изменять оптическую длину резонатора, коэффициент отражения четырёхволнового преобразователя излучения с ростом интенсивности волн накачки монотонно увеличивается. Характер изменения коэффициента отражения от интенсивности волн накачки как при наличии, так и при отсутствии кольцевого резонатора совпадает [16]. Скорость изменения коэффициента отражения с увеличением интенсивности волн накачки возрастает, при этом увеличивается также и выигрыш в коэффициенте отражения за счёт использования кольцевого резонатора. Причём значения интенсивностей волн накачки, при которых начинает нарушаться линейная зависимость между коэффициентом отражения и нормированной интенсивностью волн накачки как при наличии, так и при отсутствии кольцевого резонатора, совпадают.

Если при сопряжении кольцевым резонатором граней нелинейного слоя совпадение значений коэффициентов отражения, полученных с использованием аналитического выражения (18) и численным методом с погрешностью ±4 %, наблюдается до нормированной интенсивности G0 = 0,001, то при условии компенсации фазового набега, возникающего вследствие самовоздействия волн накачки, путём подбора расстояния L – до значения нормированной интенсивности G0 = 0,02. На порядок возрастает диапазон интенсивностей волн накачки, в пределах которого зависимость коэффициента отражения от интенсивности волн накачки описывается аналитическим выражением (18).

Заключение

Для четырёхволнового преобразователя излучения на тепловой нелинейности при наличии обратной связи на комплексные амплитуды объектной и сигнальной волн получено аналитическое выражение, связывающее при малом коэффициенте отражения пространственные спектры этих волн. Показано, что наличие обратной связи не меняет пространственную селективность четырёхволнового преобразователя и позволяет в 4–5 раз повысить его амплитудный коэффициент отражения.

При больших интенсивностях волн накачки, когда необходимо учитывать как самодифракцию волн накачки, так и перекачку энергии не только из сигнальной волны в объектную, но и из объектной волны в сигнальную, при сопряжении кольцевым резонатором граней нелинейного слоя, рост интенсивности волн накачки из-за самовоздействия этих волн может приводить не к увеличению, а к уменьшению коэффициента отражения четырёхволнового преобразователя излучения. Компенсация фазового набега, возникающего в нелинейной среде вследствие самовоздействия волн накачки, позволяет с ростом интенсивности волн накачки монотонно увеличивать коэффициент отражения четырёхволнового преобразователя излучения. Причём скорость роста коэффициента отражения существенным образом зависит от параметров кольцевого резонатора.