Численная методика расчета полушага подачи заготовки при прошивке труб на станах поперечно-винтовой прокатки

В конце XIX века братьями Манессман был предложен способ производства толстостенных труб (гильз), при котором заготовка подается в пространство между двумя валками, вращающимися в одну сторону. Валки при этом установлены так, что их оси скрещены под некоторым углом друг к другу. При контакте с валками заготовка получает поступательное и вращательное движение. Для обеспечения изготовления отверстия на пути движения заготовки устанавливается оправка, которая формирует внутренней диаметр [1, 2].

Если мы будем рассматривать, как деформируется элемент заготовки маленького объема, с какими степенями деформации, как происходит в нем накопление деформации, сколько циклов деформации материал претерпевает, то нам необходимо знать величину полушага заготовки. Существует множество формул и методик для определения шага (полушага) подачи [3], при этом большинство из них не учитывают непрерывное изменение скорости течения металла по длине очага деформации.

Введем определение местного (локального) полушага подачи: величина, характеризующая смещение точки за пол-оборота, при условии, что скорость движения точки не изменялась. Легко получить формулу для опре- деления локального полушага из условия, что точка делает полшага за то время, пока проворачивается на 90°:

S ( z ) _  п

^{и (} z )    ю ( z )) ,

где S(z) – локальный полушаг подачи в данной точке; п - число Пи, угол, на который повернулась точка; и(z) - проекция линейной скорости течения металла на ось z; ю(z) - угловая скорость вращения заготовки в сечении z.

Заменим и(z), ю(z) на проекции скорости валка с использованием коэффициентов проскальзывания:

S ( z ) -.( .O z ) d ( z ), ^{2 и} В r ⁽ z ) П т⁽ z )

где u _Bo ( z ) - проекция скорости элементарного объема на поверхности валка (которая контактирует с элементом поверхности металла) на ось z в точке z ; и _В r ( z ) - вторая составляющая скорости этой же точки, которая определяет тангенциальную скорость движения заготовки; П о ( z ) и n _T( z ) - коэффициенты осевого и тангенциального проскальзывания соответственно; d ( z ) – диаметр валка в данной точке.

Отношение проекций скорости валка пропорционально тангенсу угла подачи, учитывая это, получим:

$ ( z ) = 1 п d ( z )tg ( P )^ .           (3)

²              П т ^{( z} )

Формула (3), по сути дела, является вариацией формулы Осадчего (4) [3], где используется начальный диаметр гильзы, и для пересчета его в диаметр данного сечения вводится отношение площадей сечений Осадчего (5) [3].

$ ( z) = 1 П d Заг tg ( P )^ FT-       (4)

²             n _T( z ) F ^{( z} )

где FГ – площадь сечения гильзы, F(z) – площадь сечения заготовки; dЗаг – диаметр заготовки.

Осевая скорость элементарного объема по ходу движения от одного валка к другому непрерывно растет, формулы (3) и (4) этого не учитывают и поэтому дают возможность определить только локальный или местный шаг подачи (при условии отсутствия вытяжки). Реальный шаг подачи не совпадает с мгновенным, поскольку сам мгновенный шаг подачи постоянно изменяется.

Пусть за малое время dt элемент металла проходит расстояние dS , в начальный момент времени скорость элемента и(z), за время dt увеличивается на dи(z), при этом элемент объема поворачивается на некоторый угол dф(z) со скоростью to(z), которая через расстояние d$(z) становится ю(z) + dю(z).

Таким образом, можем записать равенство

2dS dt =-------------

2 u ( z ) + d u ( z )

d ф

2 to ( z ) + d to ( z )

Разбиваем весь очаг деформации через равные интервалы dz , т. е. на некоторое количество точек N . Для каждой точки i = [1.. N ]

рассчитываем скорость течения металла на основе анализа кинематики процесса прошивки.

В точках, где z_t <  z _Кон, значение полушага подачи легко рассчитать по формуле (2) или (9):

$ ^{( i} ) = ^{п -}        , при ^z i <  ^z Кон .            ⁽⁶⁾

to ^{( ,} )

Чтобы учесть величину шага подачи на участках, где скорость течения металла меня- ется, т. е. выполняется условие zi > zКон, оп- ределим величину углового смещения за вре- мя движения между двумя точками zi । и zi по формуле

A f = _ю ( ^{, ) +} _ю ^{( ,} - 1 ) dz ,

U z ( i ) + U z ( i - 1)

что справедливо для расчета углового смещения в прилежащем к zi отрезке. Для расчета углового смещения между другими точками на других отрезках, например: zi । „.zi-2, z,-2 „. z,-3, z,-3 „. z,-4 и т. д., введем переменную j, для первого цикла присвоим ей значение j = 1. Тогда формулу (7) можно переписать следующим образом:

Л,     ™ ( ⁱ — j ) + “ ( ⁱ — j — 1 ) ,

A f j = — -------------- -dz .

^U z ⁽ i ^- j ) ^{+ U} z ⁽ i ^- j ^- 1)

Сечение с номером i будем считать условно неподвижным. Угловые смещения границ отрезка с номером i относительно условно неподвижного сечения будем обозначать как f_a и f_b . Тогда на самом первом отрезке значения:

„                    tof i ) + to( , - 1)

f = 0; f = 0 + — k2---⁽--- L dz .     (9)

a b U z ( i ) + u z ( i - 1)         "

Для второго отрезка согласно формулам (8) и (9):

f (2) = f (1) = 0 + to(i) + to(i- 1) dz;

a b             v_z ( i ) + u_z ( i - 1)

^{z z}            (10)

f (2) = f (1)+ to(i - ‘) + m( ‘- 2) dz

Jb ⁽ ) bb ⁽ J U z ( i - I) + _u z ( i - 2)

и т. д., каждому последующему значению f_a мы присваиваем значение f_b предыдущей итерации, а f_b присваиваем значение суммы f_b с предыдущей итерации и углового смещения A f , вычисляемого по формуле (11), эти операции выполняются на шаге 5 алгоритма.

Такое постепенное увеличение f_b угла происходит до тех пор, пока f_b не становится больше п , развернутого угла.

Далее мы рассчитываем значение координаты полушага подачи как сумму суммы длин всех рассмотренных отрезков ( j - 1 ) - dz

(п-fa )-dz и значение положения координа-fb - fa ты искомой точки относительно границ искомого отрезка:

п - f_n ) • dz

S ( i ) = ( j - 1 ) ' dz + ⁽ a )) . (11) ^fb ^fa

Значение координаты относительно границ получаем из условия подобия треугольников (рис. 1); также формула может быть выведена при рассмотрении уравнения прямой по координатам двух точек. Это вычисление производится на шаге 9 алгоритма, представленного в табл. 1.

Далее проводим вычисления в следующей точке i . Данный алгоритм отражен на блок-схеме рис. 2. Наш алгоритм позволяет точнее вычислять координату точки полоборота назад.

В практике может потребоваться решать задачу, где будет находиться рассматриваемая точка через полоборота вперед. Это можно сделать по алгоритму в табл. 2, логика его построения похожа на логику построения алгоритма 1. В сравнение с алгоритмом 1 здесь есть дополнительное условие zi+j < zСхода , (12)

где z _Схода – точка отрыва заготовки от валка.

Число элементов разбиения N может быть меньше, чем значение i + j, а все векторы, используемые в расчете, имеют размерность N. Так как по мере движения вдоль оси z, при z большем чем zСхода , скорость постоянная, то для расчета углового смещения на этом отрезке мы можем использовать формулу fb = fb +

®^{( n} Схода )  ,

—7-------г • dz.

^u( n Схода )

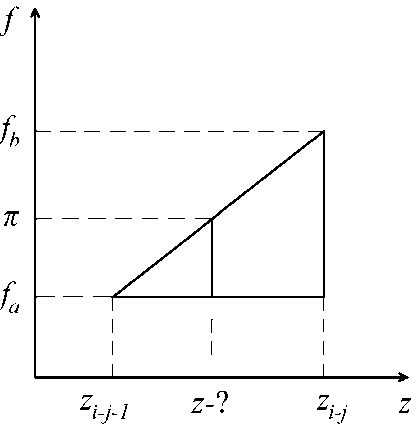
Рис. 1. Схема к формуле (11), dz = z_z - j - z_{z -} j _{- 1}

Таблица 1

Алгоритм расчета величины полушага «назад»

1	U ( i ) Если z i <  z к он, то S i = п • —— , иначе к шагу 2 ю ( i )
2	tof i ) + m( i -1) fa = 0; fb       ----(----- dz ; j = 1 a              U z ( i ) + U z ( i - 1)    J
3	Если f b <  п ; то пункт 4, иначе к шагу 9
4	f a = fb
5	Если i - j >  2 , то шаг 6, иначе шаг 7
6	to ( i - j ) +to ( i - j - 1 ) fb = fb + —"-------"------- dz , к шагу 9 b        U z ( i - j ) + U z ( i - j - 1)
7	=       to ( 2 ) +to ( l ) fb  fb +    /^x     d\^Z U z (2) + U z (1)
8	j = j + 1, к шагу 3
9	(п - L, ) • dz , x S = ( ,        + ( j - 1 ) ' dz fb fa

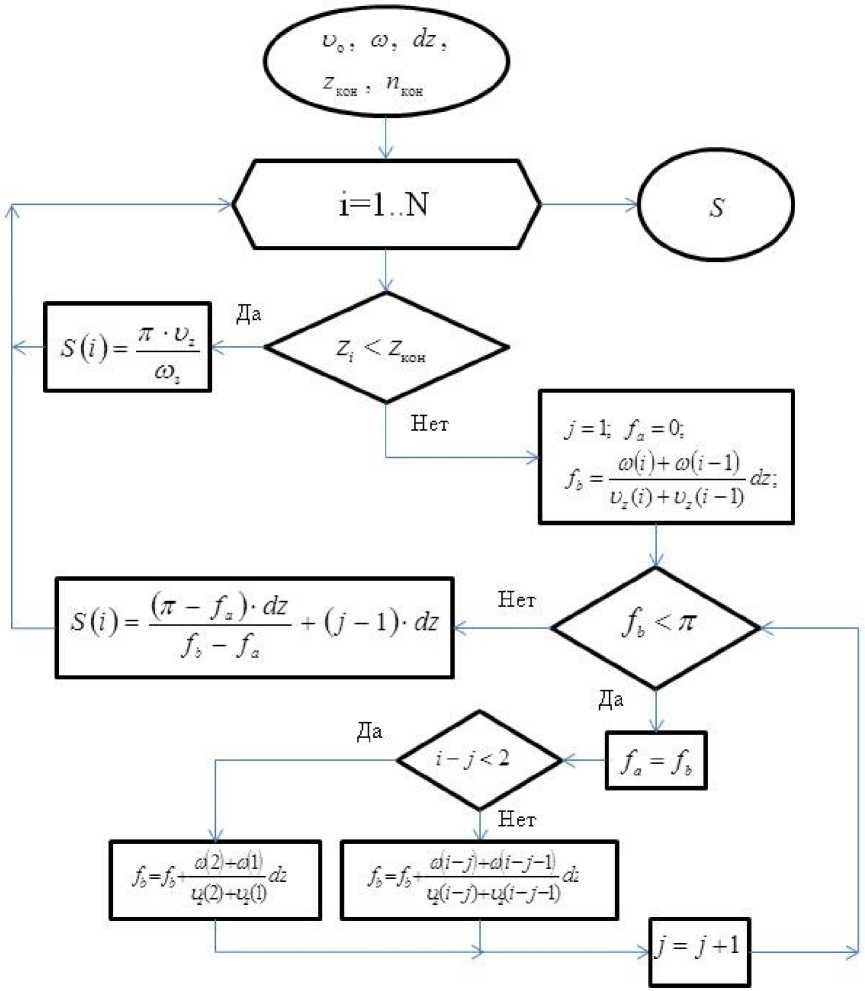
Рис. 2. Блок-схема к алгоритму расчета полушага подачи «назад»

Таблица 2

Алгоритм расчета значения полушага «вперед»

1	Если zt <  z Схода , то к шагу 1, иначе к шагу 10
2	„             ю( i ) + ю ( i + 1 ) - fa = 0; fb = _—— ——dz ; J = 1 a             U z ( i ) + U z ( i + 1)     J
3	Если fb <п , то к шагу 4, иначе 9
4	f a = f b
5	Если z i + j <  z Схода то к шагу 6, иначе 7
6	ю ( i + j ) + ro ( i + j + 1 )                      „ f b = f b +   ,.   . у . ;.dz , после к шагу 8 U z ( I + J ) + U z ( i + J + 1)

Окончание табл. 2

7	f         ^( n Схода ) • dz f b   f b +            s и z ( n Схода )
8	j = j + 1; к шагу 3
9	S ( i ) = —— fb- dz + j • dz fb - fa
10	S ( i ) = ^^ U O«) ® ( i )

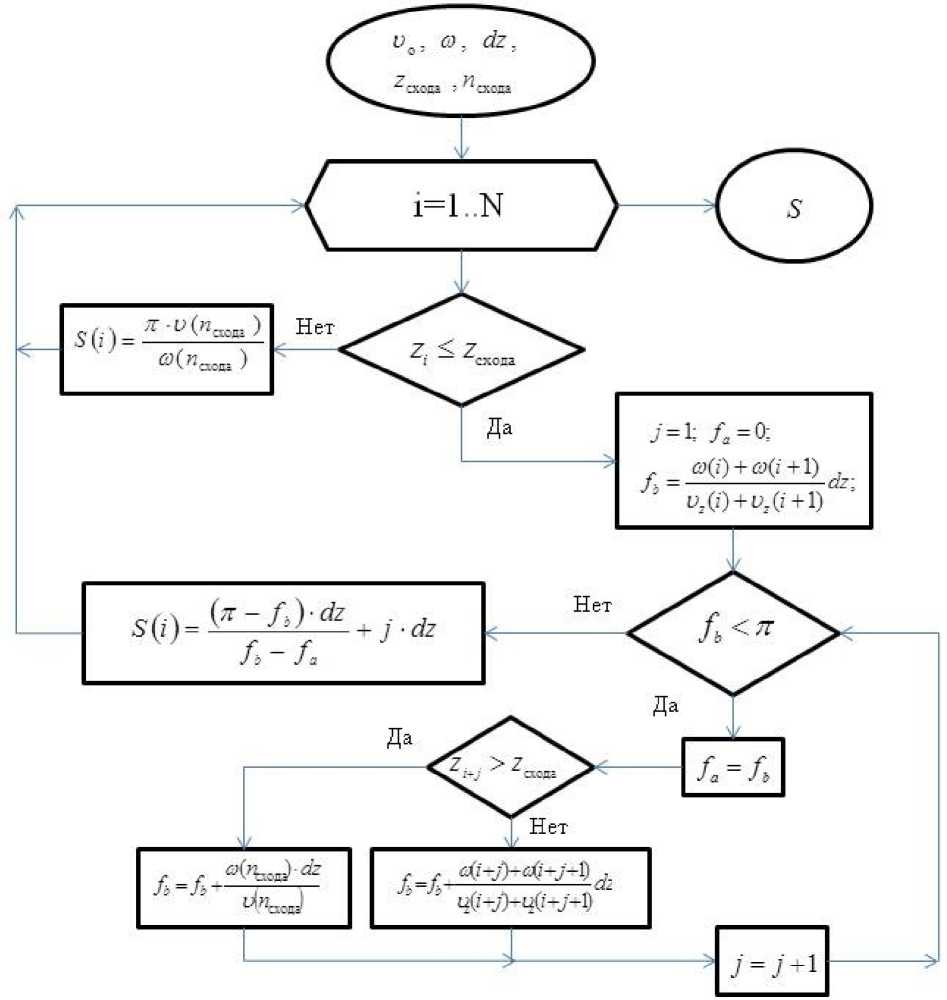
Рис. 3. Блок схема к алгоритму расчета полушага подачи «вперед»

Таблица 3

Некоторые характеристики процесса прошивки

Диаметр заготовки, мм	460
Диаметр гильзы, мм	500
Диаметр сверления в заготовке, мм	Без сверления
Диаметр оправки, мм	325
Вытяжка	1,46
Смещение оправки за пережим, мм	30

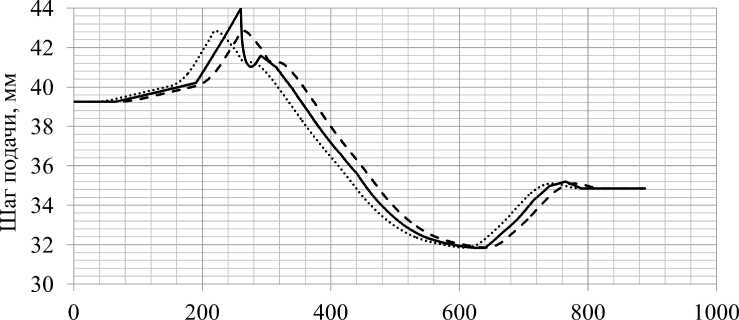
Координата положения точки вдоль очага деформации, мм

Локальный шаг подачи---Шаг подачи ’’Вперед” .........Шаг подачи ’’Назад”

Рис. 4. Результаты расчета шага подачи по разным методикам где nСхода – номер сечения, перед которым происходит потеря контакта гильзы с валком.

Далее можем рассчитать значения при другом i . Блок-схема алгоритма отражена на рис. 3.

Мы выполнили расчет шага подачи для процесса, некоторые характеристики которого представлены в табл. 3. Результаты расчета приведены на рис. 4, результаты расчета полушага подачи примерно совпадают. Графики рассчитанного нами полушага подачи не совпадают с общепризнанным их видом. По всей видимости, мы могли ошибиться при определении распределения скоростей. Однако мы получили схожие результаты расчета по нашим методикам и по формуле Осадчего. Считаем, что использование нашей методики даст большую точность расчета, и кривые шага

подачи совпадут с общепринятым видом при условии правильной задачи кинематики. При использовании для расчета формулы (4) мы можем ошибиться в значение шага подачи на 1–2 мм, и в итоге получить 1 лишнее или недосчитаться одного обжатия.