Численная модель частицы применительно к исследованию энергетических и поляризационных характеристик излучения, прошедшего через анизотропную атмосферную среду

Введение. Кристаллические облака оказывают существенное влияние на радиационные процессы, происходящие в атмосфере. Поэтому в настоящее время проблеме изучения оптических характеристик кристаллических облаков уделяется большое внимание [1 - 3]. Эта проблема решается в рамках различных международных научно-исследовательских проектов, связанных

Работа выполнена в рамках государственного задания на выполнение НИОКР и при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 12-05-00169a).

с изучением атмосферы Земли. Результатом таких исследований является разработка ряда моделей атмосферы (например, ECHAM, ECMWF, UKMO, LMD). Для дальнейшего повышения точности создаваемых моделей необходимо решить различные проблемы, возникающие, в частности, при определении оптических характеристик для несферических частиц.

Для изучения характеристик излучения, прошедшего через атмосферные образования, прежде всего следует разработать модель отдельной частицы, позволяющую адекватно установить зависимость параметров трансформированного излучения от параметров рассеивателя и падающего излучения. Проблема рассеяния и ослабления света хаотически ориентированными кристаллами рассматривалась в большом количестве работ. Однако в случае ориентированных кристаллов, особенно для ИК-области спектра, она изучена недостаточно.

Одной из важнейших оптических характеристик является ослабление. Для определения ослабления используются два способа. Первый способ основан на интегрировании вектора Пойн-тинга и законе сохранения энергии: экстинкция равна сумме рассеяния и поглощения. В частности, для отдельной частицы справедливо соотношение

° ext a’ab s ^ ° sc , где S_ext - сечение ослабления; S_abs - сечение поглощения; S_sc - сечение рассеяния. В основе второго способа лежит "гипотетический эксперимент", в результате которого определяется ослабление. Этот способ основан на интерференционном аспекте экстинкции: экстинкция равна интерференции между падающим и рассеянным в направлении вперед излучением [4].

При расчете оптических характеристик для мягких частиц, показатель преломления которых близок к единице, как правило, используется метод аномальной дифракции [1 - 4]. Полное поле, рассеянное в направлении вперед, формируется в результате когерентного сложения дифракционного и рефракционного полей. При этом фактор ослабления осциллирует в окрестности значения, равного двум. При построении моделей кристаллического облака следует учитывать, что показатель преломления ледяных частиц существенно отличается от единицы, особенно при рассмотрении оптических характеристик в ИК-диапазоне длин волн.

Для крупных полупрозрачных кристаллов поле, рассеянное в направлении вперед, определяется, главным образом, дифракционным полем. В этом случае сечение ослабления равно удвоенной площади геометрической тени частицы в направлении распространения излучения [4, 5]. Это возможно в том случае, если рефракционные пучки затухают внутри кристалла либо на выходе существенно отклоняются от направления вперед. Такой подход обеспечивает удовлетворительную точность, когда расчеты экстинкции проводятся для больших хаотически ориентированных кристаллов. При определении ослабления света ориентированными кристаллами, имеющими плоскопараллельные грани, следует учитывать соизмеримость дифракционного поля и поля рефракционных лучей, проходящих через частицу [6]. В сечении пучка параллельных лучей, вышедших из кристалла, фаза волны постоянна. При этом метод физической оптики позволяет естественным путем получить конечные амплитуды полей в направлении выхода пучков из кристалла. Единый подход к определению дифракционного и рефракционного полей позволяет сложить их когерентно. Следует отметить, что метод геометрической оптики ограничивает возможности корректно сложить эти поля. Численное исследование, проведенное в данной

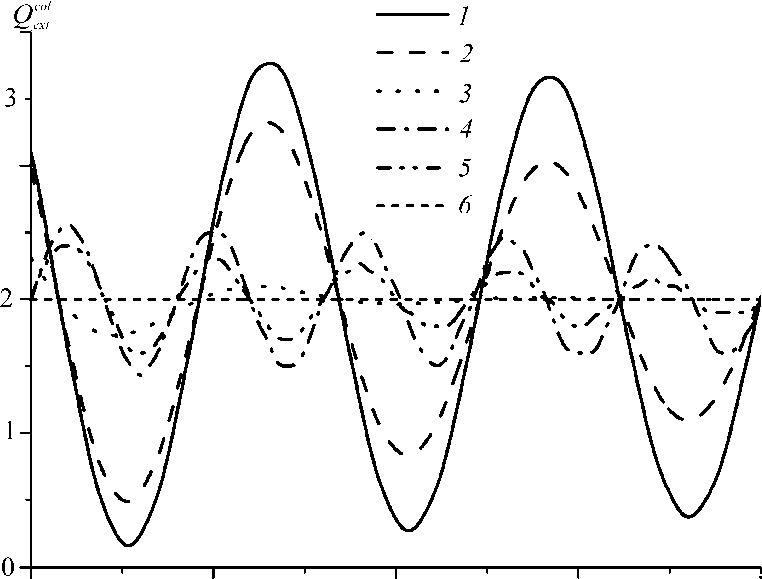
20             40              60              80             <7, мкм

Рис. 1. Зависимость фактора эффективности ослабления от толщины кристалла при различных значениях показателя поглощения ( 1 ₂/ I 1 =1, у = 0^o, а = 0^o, l = 500 мкм, Р = 60^o, X = 10,6 мкм, n = 1,31): 1 - 3 - для прямоугольного столбика ( 1 - % = 10 ⁴, 2 - % = 10 ², 3 - % 10 ’ ). 4 - 6 - для гексагонального столбика ( 4 - % = 10 ⁴, 5 - % = 10 ², 6 - % =10 ’ )

работе в рамках метода физической оптики, показало, что для ориентированных кристаллов с плоскопараллельными гранями фактор эффективности ослабления может быть отличен от двух [6, 7].

На рис. 1 представлены зависимости фактора ослабления для прямоугольного (кривые 1 - 3 ) и гексагонального (кривые 4 - 6 ) столбиков от их толщины d (угол у задает ориентацию плоскости поляризации, угол Р - ориентацию частицы относительно направления падения излучения, угол а - поворот кристалла вокруг своей оси; l - длина столбика; n , % - реальная и мнимая части показателя преломления частицы соответственно). На кристалл падает линейно поляризованное излучение (отношение параметров вектора Стокса падающего излучения I 1 / I 2 =1). Из рис. 1 следует, что для прямоугольного столбика с малой толщиной (так же, как для пластинки) фактор ослабления может изменяться в диапазоне от 0 до 4. При увеличении количества пар плоскопараллельных граней частицы интервал изменения этой характеристики сужается (для гексагонального столбика - от 1 до 3). Заметим, что чем выше значение мнимой части показателя преломления частицы, тем ближе величины ослабления к их предельному значению. В свою очередь нарушение "параллельности" граней также обеспечивает стремление фактора ослабления к асимптотическому значению, равному двум.

На рис. 2 показаны значения фактора эффективности ослабления, вычисленные для пластинчатого кристалла со скошенной гранью. Угол 0 определяет наклон верхней грани пластинки относительно ее нижней грани. С увеличением угла 0 между гранями амплитуды осцилляций быстро уменьшаются. Нарушение параллельности граней более чем на 10 ^о можно считать достаточным для того, чтобы не учитывать влияние толщи кристалла на характер ослабления оптического излучения. Если атмосферный кристалл не имеет плоскопараллельных граней, то,

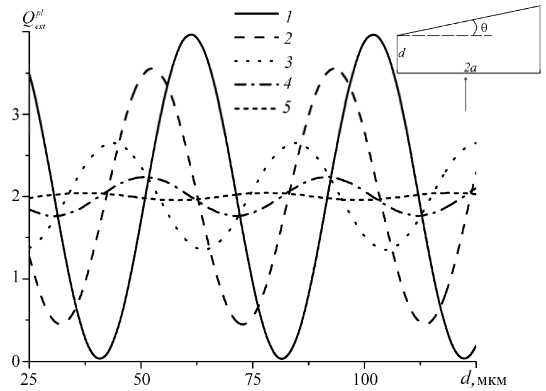
Рис. 2. Зависимость фактора эффективности ослабления от толщины пластинки со скошенной гранью ( 1 ₂/ I 1 = 1, у = 0^o, a = 250 мкм, О = 0^o, X = 10,6 мкм, n = 1,26):

1 - О = 0o, 2 - О = 2o, 3 - 0 = 4o, 4 - 9 = 7o, 5 - 9 = 10o как правило, эта "непараллельность" превышает 10°. Таким образом, среди всех крупных атмосферных частиц полупрозрачные ориентированные пластинки выделяются тем, что для кристаллов такой формы фактор эффективности ослабления может принимать значения в наибольшем интервале от 0 до 4 [6, 7].

На рис. 3 показаны зависимости Q ^* ( в ) при различных значениях длины волны и показателя преломления. Видно, что при учете рефракционного поля, когда ослабление определяется с заданной точностью, большей длине волны соответствует большее предельное значение в . На ход кривой Q C^ ( в ) существенно влияет значение показателя преломления.

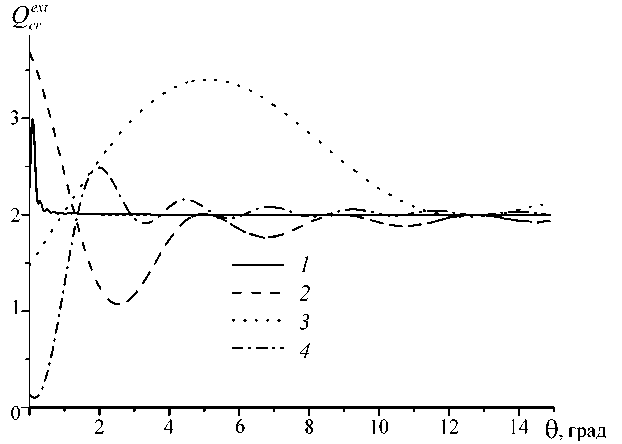
Рис. 3. Влияние на зависимость Q^e_c^x_r * длины волны падающего излучения и показателя преломления кристалла со скошенной гранью ( d = 20 мкм, a = 250 мкм): 1 - X = 0,55 мкм, n = 1,31, у = 10^-4, 2 - X = 10,6 мкм, n = 1,31, у = 10^-4 , 3 - X = 10,6 мкм, n = 1,11, у = 10^-4, 4 - X = 10,6 мкм, n = 1,51, у = 10^-4

После прохождения через ориентированную частицу могут измениться не только энергетические, но и поляризационные характеристики падающего излучения. Для полного представления этих характеристик, как правило, рассматриваются матрица рассеяния и матрица экстинкции. В данной работе с использованием метода физической оптики строится оптическая модель пластинчатого кристалла для расчета указанных матриц.

Постановка задачи. В качестве рассеивателя рассмотрим гексагональную пластинку толщиной d с длиной стороны ее основания а. Полупрозрачная ледяная пластинка имеет комплексный показатель преломления n = n + i % . Под углом 0 к основанию пластинки падает плоская волна эллиптической поляризации.

Определим оптические характеристики поля, рассеянного в передней полусфере. Передней будем называть полусферу, содержащую основание пластинки и лучи, рассеянные в направлении вперед. Для этого предлагается следующая схема решения поставленной задачи. Сначала получим полное рассеянное поле как когерентное сложение рефракционного и дифракционного полей. Далее для определения трансформированного поля в дальней зоне используем метод физической оптики и учтем все необходимые максимумы в расчетах интеграла Фраунгофера. Для характеристик излучения, рассеянного в передней полусфере, получим соотношения для сечений рассеяния, приведенных к соответствующим параметрам вектора Стокса, а также представим матрицу экстинкции.

Взаимосвязь положений источника, приемника и частицы для определения характеристик рассеяния излучения в передней полусфере. Применительно к определению характеристик рассеяния оптического излучения в передней полусфере представим необходимые угловые характеристики, связывающие положения источника, приемника и частицы (рис. 4). Пусть в точке 0 ₁ находится источник излучения, в точке О ₂ - приемник, в точке О ₃ - частица; Oхуz -абсолютная система координат, относительно которой вводятся еще три системы координат 0 ₁ х ₁ у ₁ z ₁. О ₂ х 2 у ₂ z ₂, О ₃ х ₃ у ₃ z ₃, связанные соответственно с источником, приемником и рассеивателем. Координатная плоскость Оху параллельна поверхности земли, а вдоль оси Oz направлена нормаль к ней. Направление распространения падающего излучения совпадает с положительным направлением оси 0 ₁ z ₁. Волновой вектор Пойнтинга k указывает направление падения света на основание пластины. Очевидно, что k || 0 ₁ z ₁. Электрические составляющие падающей волны эллиптической поляризации ( E ₁, E ₂ ) располагаются соответственно вдоль осей 0 ₁ x ₁ и 0 ₁ y ₁, n 1 - нормаль к плоскости падения. В качестве рассеивающей частицы представлена пластинка.

Плоскость, проходящая через основание кристалла, есть координатная плоскость О ₃ х ₃ у ₃ ортогональной системы координат О ₃ х ₃ у ₃ z ₃, 0 - угол между направлением падения излучения k (или осью 0 ₁ z ₁) и нормалью n к основанию пластинки (или осью О ₃ z ₃). Электромагнитное поле, представленное лучами, вышедшими после ряда внутренних переотражений, формируется в направлении О ₃ z ₃. Вектор k f указывает направление выхода из пластинки рефракционных лучей. Очевидно, что k || k f || О ₃ z f . Угол высоты у и угол широты ^ задают возможные положения пластинки, обусловленные ее колебаниями относительно оси О ₃ z ₃. При фиксированном значении у и при непрерывном изменении ^ от 0 до 2 л нормаль к основанию пластинки опишет ко-

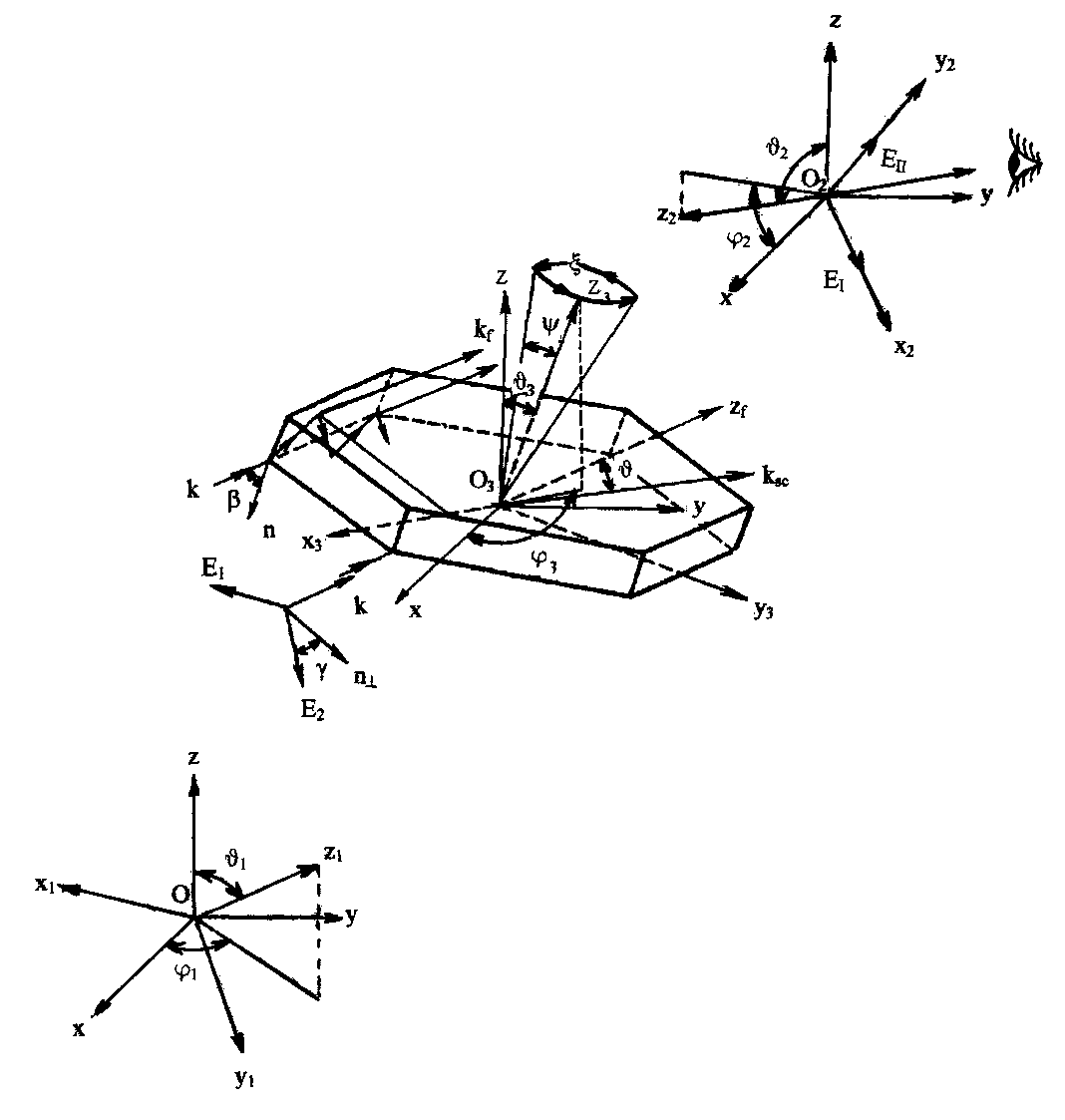
Рис. 4. Совокупность систем координат для описания рассеяния света в передней полусфере нус с осью Озzз. Прием рассеянного излучения осуществляется в направлении ksc (или оси О2z2), а ось О2у2 параллельна горизонтальной плоскости (или плоскости земли). Величины EI, Еп -составляющие поля, регистрируемого на приемнике, расположенные вдоль осей О2x2 и О2у2 соответственно. Отклонение направления приема от линии выхода лучей из пластинки (т. е. угол между направлениями О3zf и ksc) обозначим через 9.

Для представления нормированных характеристик светорассеяния достаточно определить угловое положение единичных векторов, задающих составляющие рассеянного поля. В связи с этим центры всех четырех систем координат совместим в одной точке О и определим угловые зависимости ортов ( x,y,z ) абсолютной системы координат с ортами ( x i , y i , z i ) соотношением

x

У - Si v z у

f ^x i J ^y‘

V ^z i j

i= 1 , 2 , 3,

где

f cos ф _i cos d i

S i - sin ф _i cos d i

_V - sin d i

- sin ф _i cos < д sin d? cos ф _i   sin ф _i sin d i

0 cos d _у

Очевидно, что углы d _i, ф _i определяют положение базисных векторов х i , у i , z i ( i = 1, 2, 3) каждой из трех соответствующих систем координат Oxyz ( i = 1, 2, 3) относительно абсолютной системы Oxyz .

Вращение тела в пространстве относительно декартовой системы координат принято описывать матрицей Эйлера. В связи с этим определим положение составляющих падающего поля E _i, Е ₂ в системе координат, связанной с рассеивателем. Орты систем координат О x i y i z i и О x ₃ y ₃ z ₃ можно представить с помощью линейного преобразования

x

У 3

V ^z 3 у

f ^x i )

^- " У ¹ •

V ^z i у

где

f cos a cos P cos у - sin a sin у - cos a cos P sin у - sin a cos у

A - sin a cos P cos у + cos a sin у - sin a cos P sin у + cos a cos у

- sin P cos у

sin P sin у

cos a sin P sin a sin P cos P .

Углы Эйлера a, P , у определяются как некоторые комбинации углов d _i , ф ₁ и d ₃ , ^ ₃ .

Элементы матрицы A определяют положение векторов k , E _i, E ₂ в системе координат

Ох з у ₃ z ₃. Следует отметить, что при произвольном угле ориентации плоскости поляризации у составляющие E _i, E ₂ не лежат в плоскости падения волны. Поэтому для дальнейших расчетов характеристик светорассеяния и применения к ним формул Френеля необходимо преобразовать составляющие E _i, E ₂, так чтобы одна из них была перпендикулярна плоскости падения, а другая находилась в ней. Для этой цели используем линейное преобразование

E II		f E i )
E ±	- F	E 2
V k )		V k J

где

	f- cos у	sin у	0 )
F -	sin у	cos у	0
	V    0	0	i J

Векторы E _± и E_у в системе координат, связанной с пластинкой, определяются элементами

первого и второго столбцов матрицы A_F - AF . Определим углы, задающие положение z ₂ отно-

сительно векторов Eц, E±, k f. Если матрицу В определить как S3-1 S2, то искомые проекции вектора z2 можно записать в виде cos ^x = AFU B13 + AF21 B23 + AF31 B33 ,

COS ^y = af2B13 + AF22B23 + AF32 B33 , COS ^z = af3 B13 + AF23 B23 + AF33 B33 . Учитывая, что cos^x = sin 9cos ф, cos^ y = sin 9sin ф, cos^z = cos9, нетрудно определить Э и ф. Углы Э и ф отсчитываются от направления kf. Введем новую систему координат Oxsyszs, связанную с Ox3y3z3:

	AT = AfSP . T        F
Здесь	^ cos ф cos 9 - sin ф cos ф sin 9 ^	^ cos ф sin ф 0л
	S i = sin ф cos 9 cos ф   sin ф sin 9 у - sin 9       0       cos 9   ।	, P = - sin ф cos ф 0 у 0    01 V

Электрические составляющие рассеянного поля E _s 1 и E _s 2 определяются элементами первого и второго столбцов матрицы A_T , причем эти векторы лежат в плоскости, перпендикулярной направлению приема Oz ₂ . Напомним, что E I , E _n — составляющие поля, регистрируемого на приемнике. Тогда взаимосвязь между E s , E и E I , E _n определяется с помощью линейных соотношений

E, = - cos u E_Q + sin u E_Q , E„ = sin u E_Q + cos u E_Q ,

• 1    S | S 2 ^, II S ] S 2 ^v где

cos u = A . B ₁₂ + A T. B ₂₂ + A T B ₃₂ , sin u = A T B ₁₂ + A _T^ B ₂₂ + A _T^ B ₃₂ .

После падения излучения на пластину часть его отражается в направлении л — Р , а часть проходит внутрь частицы, претерпевая преломление и поглощение. После ряда внутренних пе-реотражений вышедшие из пластинки рефракционные лучи формируются главным образом в направлении р .

Характеристики поля, рассеянного в передней полусфере. Электромагнитное поле падающей плоской волны в системе координат Ox 1 у 1 z , можно представить в виде электрической составляющей E = x 1 E 1 + y ₂ E ₂ , магнитной составляющей H = - x 1 H ₂ ⁺ У 1 ^H 1 и волнового вектора k . Заметим, что амплитуды электрических и магнитных составляющих связаны между собой, поэтому выражения для магнитных составляющих в данной работе не приводятся.

Полное рассеянное поле образуется при прохождении первичной волны через частицу. В направлении распространения падающего излучения оно является суперпозицией первичной и рассеянной волн. Для ориентированных кристаллов следует учитывать, что поле, рассеянное в направлении вперед, определяется как когерентное сложение двух соизмеримых по величине полей: дифракционного и рефракционного. Это объясняется тем, что, с одной стороны, частица ослабляет волну за счет возмущения ее фронта, обусловленного образованием в нем геометрической тени, а с другой - изъятая часть фронта после прохождения через частицу при определенных фазовых соотношениях добавляется к возмущенному фронту волны в противофазе, еще более ослабляя его.

Вектор электрической составляющей полного рассеянного поля зададим в виде Ef = E;- E,, где E. и E$ — векторы падающего и рассеянного полей, которые представляются известными соотношениями [4]

и»

E , = E e ^k , E , = A — .                            (1)

В свою очередь комплексные амплитуды соответствующих полей A = A 1 + A ₂ , A 1 ± A ₂ ,

( E = E 1 + E ₂ , E 1 ± E ₂ ) могут быть представлены в виде

Г A )

А V ^a 2 2

Г S u

V ° 21

Sn Ye^ ¹² в' ° 22 2V E 2 2

где S y — элементы амплитудной матрицы размером 2 x 2.

Для определения рассеянного поля используем метод физической оптики, который позволяет когерентно сложить дифракционное поле и поле рефракционных пучков с учетом фазовых набегов [6]:

A ' = ( Ad ' - A ^)( d o cos ^ - Ф 0 sin ф ), A ₂ = ( A D 2 - Ar )( 9 _i:sin ф + ф ₀ео8 ф ).

Отметим, что орты сферической системы координат Ф0, ф0, r0 представлены элементами матри цы AT, а углы В и р определены в системе координат Ох1у1z1, связанной с падающей волной. Согласно принципу Бабине амплитуды дифракционного поля AD и AD^ определяются по фор мулам

AD =    (1 + cos В) Ei F (В, ф) e *, AD = -k- (1 + cos В) E2 F (В, ф) e*,

'   4л                               2

где k = 2 л / X — волновое число; X — длина волны; у - фазовый набег невозмущенной части фронта волны после ее прохождения через объем, содержащий пластинку. Угловая функция F ( В , ф ) является интегралом Фраунгофера

F(В,ф) = jjexp(-kaccos фsin В - 'ky sin фsin В)dxdy ,(5)

S где S - площадь геометрической тени частицы.

Амплитуды рассеянного поля AR и AR^, прошедшего через пластинку, определяются как сумма рассеянных пучков, образующихся при многократных прохождениях через пластину части фронта первичной волны. Для расчета A^ и Ar используем следующие соотношения:

A„ = -Y(1 + cos В )( Ea + E₂a ₂),   A„ = -Y(1 + cos В )( E,a, ,+ E₂a ₂₂),

R             1112 12     R             1212 22

1 4л                                2 4л a11 = cosucosyB^ + sinu sinyB1, a12 = cosu cosyBL- cosusinyBp(6)

a ₂₁ = cos u sin y B _± - sin u cos y B^, a ₂₂ = sin u sin y B^ + cos u cos y B ₁ .

Угловые функции B ^ и B ₁ определяются как комбинации коэффициентов Френеля TpT _L , TpT _L , R,R ₁ и угловых функций рассеяния j -х пучков Fj( Э ,ф')e " :

jj

BHO,ф) = T^R^F^,ф) e*j, B±(Э,ф) = T±T±£RF(Э,ф) e*j .(7)

.i=1

Коэффициенты прохождения T, TL, T, TL и отражения R|, R± определяются известными соот ношениями t =   2n cos Э cosЭ + ncos P

T =    2 ncos Э t =    2 cos P

¹ n cos Э + cos P ¹¹ n cos P + cos Э’

• 2    cos P r = cos Э - iicos P   r = iicos O - cos P

cos P + iicos Э’    ¹¹ cos Э + iicos p’ ¹ iicos Э + cos P

Комплексный угол преломления Э определяется из закона Снеллиуса sin Э = sin Э/n , где n -комплексный показатель преломления частицы. Сомножитель F j ( Э , ф ) в (7) представляет собой интеграл Фраунгофера

F j ( Э, ф ) = Д exp( - ikx cos ф sin Э - iky sin ф sin Э ) dxdy ,                       (9)

Sj где Sj - сечение пучка, выходящего из пластины после 2j -1 прохождений через нее в направлении р. Фазовые набеги пучков различной кратности отражения обозначим через уj. В случае й=0 выражения (5) и (9) существенно упрощаются, при этом F(Э,ф) = S, Fj (Э,ф) = Sj.

Определим энергетические и поляризационные свойства излучения, рассеянного в передней полусфере. Для этого рассмотрим сечения рассеяния, пропорциональные соответствующим параметрам вектора Стокса:

⁴ ^ ^{г 2} ^fj =—,—If,                                  ⁽¹⁰⁾

( 1 ₁ - интенсивность электромагнитного поля падающей волны). Параметры вектора Стокса I_f

' j выражаются через амплитуды трансформированного поля:

If, = |E i|^{2 +} |ЕцГ, I f , = |E i|² - |Eii| ² , I f . = 2Re( ErE_n ) , I f , = 2Im( E _I E_{I I}) .                  (11)

В данной работе сечениями рассеяния будем называть все четыре величины стf , несмотря j на то что классическим сечением рассеяния является только стf . Учитывая соотношения (3)-(11) и проводя необходимые алгебраические преобразования, для сечений рассеяния получаем выражения af = W^Mij-i, j =1, 2, 3, 4, i=1         I1

где

_ k ² (1 + cos ^ )²

W —             ,

К L

• - ( i = 1, 2, 3, 4) - параметры вектора Стокса падающего излучения,

M _ | ^b11\ ⁺ IM ⁺ b 211 ⁺ b 22 |     M _— I ^b 11| ~ | ^b 12 | ⁺ b 211 ~ b 22 I

M ₁₃ — Re( b₁₁ b * + b ₂₁ b ₂*₂ ), M ₁₄ — ~ Im( b ₁₁ b * + b ₂₁ b ₂*₂ ),

_{M —} | b 11| ² + 1 / -.Г ~ b 21Г ~ b 22^ M _— I b 11| ² ~|^ ~ b 21Г + b Г

• ²¹                     2                 ’     ²²                     2                 ’

M 23 — Re( b 11 b * ~ b 21 b 2*2 ), M 24 — ~ Im( b-b * ~ b 21 b *2 ),

M 31 — Re( b-b 2*1 + b 21 b 2*2 ), M 32 — Re( b-b 2*1 ~ b 1₂ b 2*2 ),

M 33 — Re( b-b 2*2 + b 12 b 2*1 ), M 34 — ~ Im( b-b * ~ b^b 2*1 ),

M ₄₁ — Im( b₁₁ b * + b ₁₂ b ₂*₂ ), M ₄₂ — Im( b₁₁ b * ~ b ₁₂ b 2₂ ),

M ₄₃ — Im( b₁₁ b*^ + b ₁₂ b ₂*₁ ), M ₄₄ — Re( b₁₁ b ₂*₂ ~ b ₁₂ b ₂*₁ ) .

Элементы матрицы рассеяния M ij представляют собой комбинации элементов b_kl ( k=1, 2; l =1, 2) (или элементов амплитудной матрицы (2)). Следует отметить, что величины b kl и S_kl различаются только коэффициентом. Элементы b_kl определяются как разность соответствующих составляющих амплитуд дифракционного и рефракционного полей (3).

После прохождения падающего излучения через частицу с фиксированной ориентацией в пространстве могут измениться не только его энергетические, но и поляризационные характеристики. Для полного описания процесса ослабления введем так называемую (4 х 4)-матрицу экстинкции K . Физический смысл матрицы экстинкции состоит в следующем. Рассмотрим пучок параллельных лучей, распространяющихся в направлении k через среду, содержащую частицу. Изменение вектор-параметра светового пучка I(k) вдоль части пути ds описывается уравнением [1]

d I ^ k ) — - K ( k ) I ( k ) .

ds

Матрица K может быть представлена в виде суммы двух когерентных слагаемых. Одно из них содержит характеристики трансформированного излучения, для которого различные компоненты поляризованного падающего поля после прохождения через среду по-разному поглощаются, другое характеризует ситуацию, когда указанные компоненты по-разному преломляются, обеспечивая анизотропность среды [8].

В работах [1-3, 8] выражения, описывающие матрицу экстинкции (МЭ), получены на основе оптической теоремы с использованием вектор-параметрического описания. В этих работах изложен вывод МЭ (а в [2] и ее разновидности - амплитудная матрица экстинкции, матрица экстинкции Стокса) в операторной форме. Такой подход определяет связь МЭ с параметрами вектора Стокса и амплитудной матрицей. На заключительном этапе вывода каждый элемент матрицы экстинкции представляет собой линейную комбинацию элементов амплитудной матрицы. Матрица экстинкции, полученная на основе оптической теоремы, может быть представлена в следующей форме:

к _

k

Re ( S 11 + S 22 )

Re ( S _u - S 22 )

Re ( S 12 + S 21 )

Im ( S 12 - S 21 )

Re ( S 11 - S 21 ) Re ( S _H + S 22 ) - Re ( S 12 - S 21 )

Im ( S 12 + S 21 )

Re ( S 1 Re ( S ,

Re ( S 1

- Im ( S 1

+ S 21 )

S 21 )

^{+ S} 22 ⁾

S12 )

- Im ( S „ - S 21 ) - Im ( S 12 + S 21 )

Im ( S 11 - S 22 )

Re ( S 11 + S 22 )

Из (12) следует, что для элементов матрицы К справедливы соотношения К 11 _ К 22 _ К ,, _ К 44 , К 12 _ К 21 , К 13 _ К 31 ,

14          41 ,    -*^v32          23 ,        24          42 ,       34          43 ^.

Для отдельной частицы сечение экстинкции определяется через элементы первой строки матрицы (12) [2]:

S „ ^_ К ^{11 +} К ¹² I ^{2 +} К ¹³ 1 1 ⁺ к ¹⁴ I • .

Для представления сечения ослабления в случае поляризованных полей используется известная формула [4]

S_

_ 4 ^ Re { EA| _s o }

k ²      E * E

Один из основных выводов, который следует из анализа (13), состоит в том, что излучение различной поляризации ослабляется по-разному [6]. Заметим, что выражение (13) представляет собой одну из частных форм оптической теоремы. Общность выражений (12), (13) становится более очевидной, если в первом из них в качестве множителя ввести величину 4 ^ k ². В ряде представлений матрицы экстинкции этот коэффициент опускается, но он, очевидно, учитывается при определении S_lj . В представлении (12) элементы матрицы экстинкции имеют размерность площади (так же как и величина S_ex t (13)). В данном случае в выражение для элементов амплитудной матрицы 8^. в качестве сомножителей входят квадрат волнового числа и дифракционный интеграл, имеющий размерность площади [4]. Следует отметить, что для пластинок в случае рассеяния в направлении вперед (т. е. при 9 = 0°) для элементов амплитудной матрицы справедливо соотношение S ₁₂ = S 21 (так же как для a ₁₂ = a ₂₁ и b ₁₂ = b ₂₁), а значит, элементы матрицы экстинкции, определяемые как разность S ₁₂ и S ₂₁ , обращаются в нуль.

Термин "сечение экстинкции" является классическим. Этим и объясняется выбор названия матрицы (12) как "матрицы экстинкции". Следует отметить, что существуют и другие названия матрицы (12). Различаются также формы ее представления [1, 2, 8] , главным образом, в зависимости от исходного описания рассеянного поля (см. соотношения (1)). Однако при расчетах значений элементов МЭ получается один и тот же результат, поскольку одна форма представления рассеянного поля сводится к другой. Также следует отметить, что элементы амплитудной матрицы и дифракционный интеграл могут рассматриваться как безразмерные величины либо иметь размерность длины или площади. В этом случае указанные соответствующие характеристики различаются, как правило, только множителем.

Заключение. С использованием метода физической оптики для исследования характеристик электромагнитного излучения, прошедшего через атмосферные ледяные образования, разработана численная модель. В качестве отдельной частицы рассмотрена полупрозрачная пластинка, для которой свойствен наибольший интервал возможных значений фактора ослабления 0^4. С помощью метода физической оптики получены соотношения для элементов матриц рассеяния и экстинкции с учетом возможных колебаний частиц относительно их устойчивого положения. Эти выражения позволяют рассчитать как энергетические, так и поляризационные характеристики светорассеяния в зависимости от размеров частиц и показателя преломления при различных положениях источника, приемника и рассеивателя, а также при любом значении длины волны из оптического диапазона и любом состоянии поляризации падающего излучения. Представленная численная модель позволяет исследовать сложную структуру зависимости рассеяния вблизи направления вперед.