Численная модель образования аневризмы сосудистого протеза

Сосудистые протезы биологического происхождения являются перспективными конструктами для решения проблемы нехватки донорского материала при сосудистых вмешательствах [1, 2]. Такой подход предполагает концепцию минимального иммуновоспалительного ответа на имплант за счет химического маскирования антигенов с сохранением экстрацеллюлярного матрикса из коллагена, эластина и гликозаминогликанов [1]. Предполагается, что такие сосудистые протезы превосходят синтетические сосуды по параметрам гемосовместимости и более физиологичному механическому соответствию между имплантом и областью имплантации [3]. Большинство таких коммерческих протезов на основе ксеногенного материала Artegraft®, ProCol®, и на основе технологии SynerGraft® используют узко специализированно [1]: для гемодиализного доступа или для шунтирующих вмеша- тельств на периферических сосудах. Такая ограниченная область применения данных изделий обусловлена специфическими недостатками, которые не позволяют им полноценно конкурировать с более технологичными полимерными сосудами на основе ePTFE или Dacron, применяемыми значительно более часто.

Одним из основных клинически наблюдаемых осложнений подобных сосудов является образование аневризм [1], причина которых заключается в деградации механических свойств сосудистой стенки, возникающей в результате агрессивной обработки – децеллюляризации или постепенной деструкции клетками иммунной системы [4]. Сосудистый протез подвергается воздействию системного кровяного давления и воспалительному ответу сразу после имплантации, и аневризмообразование именно в раннем периоде является ключевой причиной неудачи таких протезов в клинике [5].

Углубленное исследование биомеханических причин данного явления и потенциальных путей для снижения риска аневризмообразования может быть основано на моделировании такого процесса. Одной из методик исследования биомеханики тканей сосудов и сосудистых протезов является численное моделирование, активно представленное в современной литературе. Однако основной акцент в данных работах сделан на уже сформированном аневризматическом изменении сосуда и его влиянии на гемодинамику [6], риск разрыва аневризмы [7], тромбоз, выбор стратегии хирургического лечения [8]. Ряд исследователей демонстрируют технические особенности создания трехмерных моделей аневризм на ос- нове клинических данных [9, 10], настройки для расчетов в различных программных комплексах [11, 12]. Непосредственно моделирование процесса роста аневризмы также представлено в литературе, однако оно носит упрощенный характер за счет линейной геометрии сосуда [13] или недетальной геометрии самого патологического участка (шар) [14] (рис. 1).

В связи с этим настоящее исследование посвящено детальному in silico моделированию процесса образования аневризматического расширения на примере сложной трехмерной геометрии с имитацией деградации свойств сосудистой стенки в процессе многоцикловой нагрузки.

b

a

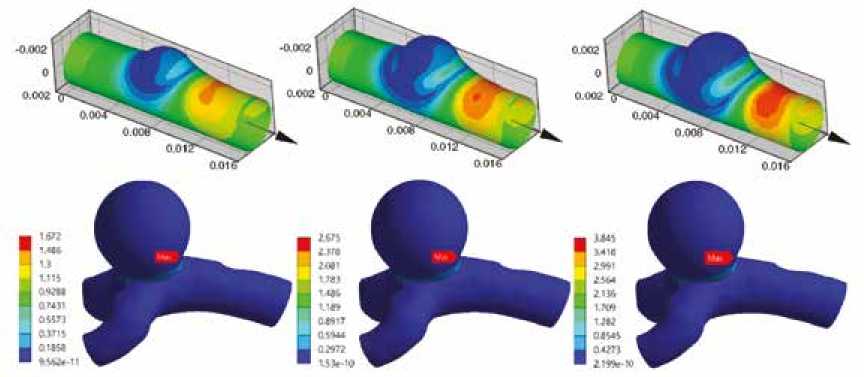
Рис. 1. Примеры численного моделирования процесса аневризмообразования, описанные в литературе: а – на основе цилиндрической модели сосуда [13], б – на основе пациент-специфической модели [14]

Fig. 1. Examples of numerical simulation of the process of aneurysm formation described in the literature: a – based on a cylindrical vessel model [13], b – a patient-specific model [14]

Материал и методы

В качестве объекта исследования, для которого продемонстрировано моделирование аневризмообразова-ния, выбрали сосудистый протез – «КемАнгиоПротез» (ЗАО «НеоКор», Кемерово, Россия), выполненный из внутренней грудной артерии крупного рогатого скота. Диаметр просвета сосуда составил 5 мм. Стабилизирован материал диглицидиловым эфиром этиленгликоля (ЗАО «НеоКор», Кемерово, Россия). Основная область применения данного изделия – постоянное замещение сегментов сосудистого русла человека, прежде всего периферических артерий. В настоящем исследовании выбран участок сосудистого протеза, который имеет значительную вариативность толщины стенки и является вследствие этого выбракованным. Данный участок выбран для наиболее наглядной демонстрации примененной методики.

Для проведения численного эксперимента получали точную трехмерную модель исследуемого сосуда методом компьютерной микротомографии на экспериментальной установке «Орел-МТ», (Россия). Характеристики: напряжение – 80 кВ, ток – 48 мкА, время экспозиции кадра – 0,667 с, число кадров в проекции – 3 шт., число проекций – 1200 шт., угловой шаг – 0,3 град., размер вок-селя – 25,4 мкм. Представленные томографические сре- зы импортировали в среду Mimics (Materialize, Бельгия), реконструируя объемную трехмерную фасетную модель (рис. 2а). Таким образом, была получена stl-сетка из гек-саэдрических элементов, пригодных для исследования методом конечных элементов (рис. 2б), итоговое количество 538 тыс. шт.

Для получения механических свойств сосудистой стенки, которые должны быть применены при численном моделировании образования аневризмы, проводили in vitro испытание в условиях модифицированного теста одноосного растяжения. Этап предполагал исследование образцов длиной 60 мм ( n = 5) сосудистых протезов на универсальной испытательной машине Z50 (Zwick/Roell, Германия). Все образцы растягивали продольно со скоростью 20 мм/мин до разрыва, регистрируя пары «сила растяжения – деформация».

Моделирование процесса аневризмообразования осуществляли в среде Abaqus/CAE (Dassault Systemes, США), имитируя многократное циклическое воздействие давления (150 условных циклов), характерного для периферических артерий человека (рис. 2 г ) [15], на внутреннюю поверхность трехмерных микротомографических моделей (рис. 2 в ). В расчетах использовали линейный материал, представленный модулем упругости и кривой пластической деформации, соответствующий результатам натурных исследований механических свойств.

a

б

в

г

Рис. 2. Визуализация компьютерной микротомографии сканированных сосудистых протезов и реконструированная на их основе сетка конечных элементов: а – протез в полном спектре рентгенологической плотности, б – визуализации сетки конечных элементов в среде Abaqus/CAE, в – визуализация приложения давления и участков ограничения от передвижения (граничные условия), г – пример приложения знакопеременной амплитуды давления на внутреннюю поверхность протеза, д – визуализация продольного растяжения сосудистого протеза в универсальной испытательной машине (представлен момент, близкий к разрыву образца)

Fig. 2. Visualization of computed microtomography of scanned vascular prostheses and the finite element mesh reconstructed on their basis: a – prosthesis in the full range of radiological density, б – visualization of the finite element mesh in the Abaqus/CAE environment, в – visualization of the application of pressure and areas of restriction from movement (boundary conditions), г – an example of the application of a sign-variable amplitude of pressure on the inner surface of the prosthesis, д – visualization of longitudinal stretching of a vascular prosthesis in a universal testing machine (the moment close to sample rupture is presented)

Модуль упругости для биологической части составил 1 МПа, предел пластичности равен 0,6 мм/мм по деформации.

Для задачи воспроизведения процесса аневризмообра-зования в линейную модель материала биологической части была включена функция деградации модуля упругости в зависимости от уровня возникающей деформации в стенке сосуда при воздействии давлений. Пороговым значением для включения такой деградации стал условный предел пластичности (0,6 мм/мм), при котором кривая «сила растяжения – деформация» материала теряет свою линейность. Данную функцию реализовывали за счет включения такого поведения в сабрутину USDFLD Abaqus/CAE. Настройки моделирования деградации были подобраны таким образом, чтобы постепенно реализоваться при приложении не более 150 циклов нагрузки циклическим давлением от 0 до 120 мм рт. ст. (рис. 2г). В ходе моделирования оценивали диаметр, радиальное перемещение (U1), амплитуду пластической деформации (PE), а также степень деградации модуля упругости сосудистой стенки, в разгруженном состоянии наиболее измененной области протеза.

При описании количественных результатов исследования использовали медиану ( М ), 25-й и 75-й процентили, максимум и минимум.

Результаты

Исследование механических свойств сосудистого протеза показало высокую вариативность в повторах, что видно и по кривым «сила растяжения – деформация» (рис. 3). Продемонстрирована «классическая» нелинейная J-образная кривая механических характеристик биоматериала [16], которая обусловлена гетерогенной структурой сосудистой стенки, представленной извитыми молекулами коллагена и эластина.

Для определения модуля упругости биологического сосудистого протеза, который должен быть применен как исходный при моделировании, был выделен начальный участок кривой – в диапазоне малых, околофизиологи-ческих нагрузок, до 1% деформации, рассчитан модуль упругости для использования в рамках линейной модели с деградацией свойств. Начальным модулем упругости принимали 1 МПа.

Численное моделирование процесса аневризмообра-зования ожидаемо продемонстрировало, что с ростом номера цикла нагрузки происходит постепенное накопление пластической деформации и плавное снижение модуля упругости, т. е. реализуется заложенная модель деградации (с помощью сабрутины USDFLD). При этом такие изменения в модели происходили неравномерно – в зависимости от толщины стенки сосудистого протеза. Наибольшие изменения свойств наблюдали для участка малой толщины – к 150 циклу нагрузки остаточный модуль упругости для такой области составил 10% от исходного (т. е. 0,1 МПа при начальном 1 МПа). При этом наблюдали значительное выпячивание сосудистой стенки в данном месте по типу аневризматического (рис. 4) – в радиальном направлении до 0,7 мм. Такая амплитуда не характерна для других областей: после снятии нагрузки остаточное радиальное перемещение составило до 0,43 мм. Пластическая деформация (показатель max. principal PE) составила максимально 0,55%. Эпюры деформации наглядно демонстрируют данные особенности (рис. 5).

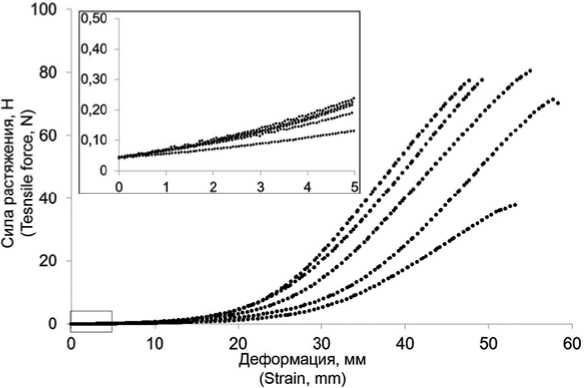
Рис. 3. Графики «сила растяжения – деформация» исследования механических свойств сосудистого протеза в условиях одноосного растяжения. Дополнительно визуализирован начальный участок кривой, ставший основой для выбора модуля упругости при моделировании

Fig. 3. Graphs of “stretching force – deformation” of the study of mechanical properties of vascular prosthesis under uniaxial tension. In addition, the initial section of the curve is visualized, which became the basis for choosing the elastic modulus in modeling

Рис. 4. Эпюры численного моделирования, визуализирующие степень деградации модуля упругости материала сосуда, в результате воздействия циклической нагрузки (условных 150 циклов приложения давления): начальное и итоговое состояние после моделирования

Fig. 4. Diagrams of numerical simulation visualizing the degree of degradation of the elastic modulus of the vessel as a result of cyclic loading (conditional 150 cycles of pressure application): initial and final state after simulation

Начальное состояние (Initial form)

25й цикл нагрузки (25th loading cylce)/

50й цикл нагрузки (50th loading cylce)

ЮОй цикл нагрузки 150й цикл нагрузки (100th loading cylce) (150th loading cylce)

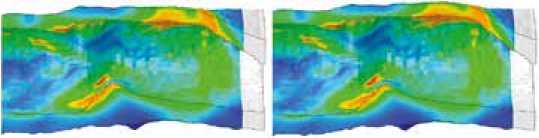
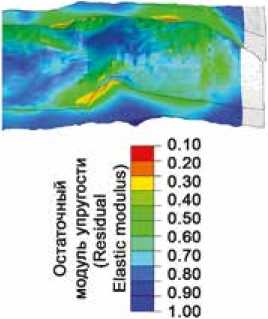
Рис. 5. Реализация механизма аневризмообразования в численном эксперименте: пример эволюции выпячивания стенки одного из концов сосудистого протеза при росте числа циклов нагрузки, изображения представлены в продольном срезе. Стрелками акцентировано внимание оставшихся выпяченными участках сосудистой стенки после снятия давления

Fig. 5. Implementation of the mechanism of aneurysm formation in a numerical experiment: an example of the evolution of the wall protrusion of one of the ends of the vessel with an increase in the number of load cycles, the images are presented in a longitudinal section. The arrows focus on the remaining protruding areas of the vascular wall after pressure relief

Обсуждение

Исследование механических свойств сосудистых протезов подтверждает высокую вариативность кривых «сила растяжения – деформация», обусловленную природой протеза, – биологические материалы обладают ожидаемо большей неоднородностью геометрических и структурных характеристик [17], которые в итоге проявляются в различиях механического отклика. Однако область малых деформаций, анализ которой и стал основой для выбора модели материала при расчетах, продемонстрировала условную однородность, благодаря чему удалось определить начальное значение модуля упругости, равное 1 МПа. Данные результаты сходятся с собственными исследованиями, проведенными ранее [18], описывающими механические свойства сосудистых протезов биологического происхождения.

Численный анализ особенностей образования аневризматических изменений в стенке сосудистого протеза позволил оценить концепцию представленного метода моделирования. Наглядно показано, что при описанной постановке некоторые участки протеза подверглись значительным изменениям свойств материала (модуля упругости) и его геометрии в виде аневризмоподобного выбухания. Такое моделирование реализует две основные особенности биомеханики сосудистого протеза: как только напряжение превышало пороговое значение предела пластичности (0,6 мм/мм), возникала пластическая необратимая деформация, и одновременно снижался модуль упругости.

Для областей, в которых пороговое значение напряжения не было превышено, таких эффектов не возникало – вся деформация была обратима, модуль упругости не падал. Вследствие такого описания модуль упругости в модели принимал значение от 100 до 10% относительно исходного, индивидуально для области сосудистого протеза (точнее, для каждого конечного элемента). При этом для «дефектных» областей каждый последующий цикл давления вызывал еще большую деградацию модуля упругости и еще большее накопление пластической деформации, что приводило к постепенному выпячиванию сосудистой стенки. Безусловно, выбранная в настоящей численной постановке модель деградации биопротеза упрощена по сравнению с некоторыми литературными моделями [19, 20]. Однако она наглядно и эффективно позволяет исследовать изменения в стенке сосуда при придании знакопеременной нагрузки малоамлитудным физиологическим, но длительным давлением.

Ограничения исследования

Важно отметить, что любые новые численные методы должны иметь верификацию в серии in vitro или для медицинских изделий – в экспериментах in vivo . Однако, учитывая длительность и малую предсказуемость процесса аневризмообразования, настоящая методика не содержит такой верификации, и результаты, получаемые с ее помощью, должны быть интерпретированы с осторожностью. Тем не менее мы предполагаем, что представленный подход к численному моделированию деградации механических свойств сосудистого протеза станет основой для первичной, предварительной оценки безопасности подобных изделий с обязательной последующей натурной валидацией в рамках конкретной задачи отдельных коллективов исследователей.

Заключение

Проведенное исследование демонстрирует метод моделирования аневризматических выпячиваний сосудистой стенки, в основе которого лежит деградация модуля упругости и накопление пластической деформации в некоторых областях протеза. При этом такой метод способен относительно быстро вызывать возникновение патологических участков, благодаря чему возможно получать результат в разумное время.