Численная модель опорного каркаса протеза клапана аорты

Клышников К.Ю., Овчаренко Е.А., Онищенко П.С., Глушкова Т.В., Акентьева Т.Н., Костюнин А.Е., Резвова М.А., Барбараш О.Л. Численная модель опорного каркаса протеза клапана аорты. Сибирский журнал клинической и экспериментальной медицины. 2024;39(3):181–187

Транскатетерное протезирование клапана аорты является одним из ведущих современных методов интервенционной кардиологии, активно применяемым в лечении приобретенных пороков клапанов сердца [1]. Данная технология, отличаясь малой инвазивностью, значительно упрощает процедуру протезирования, уменьшает время пребывания пациента в стационаре и снижает риски, связанные с открытыми кардиохирургическими операциями [2, 3]. За последние годы количество транскатетерных процедур в России значительно увеличилось, особенно это было заметно в период с 2016 по 2021 гг., когда число операций утроилось (от 511 до 1487 в год) [4]. Такой рост обусловлен разработкой новых моделей протезов, совершенствованием и оптимизацией существующих устройств. Однако до сих пор большинство таких протезов являются импортными, поэтому сохраняющаяся высокая стоимость транскатетерных систем ограничивает их массовое применение. В данном контексте значимой становится задача импортозамещения в сфере медицинских технологий, направленная на создание отечественных аналогов транскатетерных протезов, соответствующих стандартам и нуждам здравоохранения страны [5].

В современном инжиниринге медицинских изделий высокого класса риска, в том числе имплантируемых, численное моделирование является ключевым этапом проектирования. Оно предоставляет возможность провести разносторонний анализ свойств новых моделей, доведя их до фактического прототипирования и производства [6]. Метод конечных элементов (МКЭ) как наиболее распространенный пример компьютерного моделирования, на- шедший широчайшее применение в различных областях, включая инженерию и медицину, позволяет точно прогнозировать поведение протезов в условиях биологических тканей, учитывать их сложную геометрию, свойства материалов и граничные условия [7–11]. Благодаря этому МКЭ становится неотъемлемым инструментом в разработке и оптимизации медицинских изделий [12–14].

Исходя из указанных предпосылок – необходимости создания новых отечественных моделей транскатетерных протезов и доказанной эффективности МКЭ, настоящее исследование сфокусировано на компьютерном анализе первого, наиболее критичного компонента транскатетерного протеза – опорном каркасе. В работе представлены результаты оценки напряженно-деформированного состояния трех собственных 3Д-концептов данных элементов. Все модели подвергали исследованию влияния основных нагрузок, возникающих в процессе имплантации, для оценки их эффективности и безопасности применения – при придании рабочей формы и кримпировании.

Материал и методы

Объект исследования

Основой исследования стали три трехмерные компьютерные модели стентоподобных опорных каркасов, которые были созданы на основе анализа литературных данных – конструктива схожих баллонорасширяемых протезов клапанов сердца. Все модели представляют собой ряды замкнутых ячеек, которые формируют две условные зоны протеза – область крепления в фиброзном кольце клапана аорты и область поддержания створчатого аппарата протеза. Данные зоны, исходя из описанных задач, различаются конструктивно (рис. 1). Так, выводная зона (верхняя), в которой расположены комиссуральные стойки створчатого аппарата, имеет более продолговатые ячейки с повторяющимися прорезями для крепления биологического материала. В приточной зоне (нижней) ячейки более «плотные», мелкие, за счет чего формируется большая радиальная сила и большая площадь контакта с окружающими биологическими тканями.

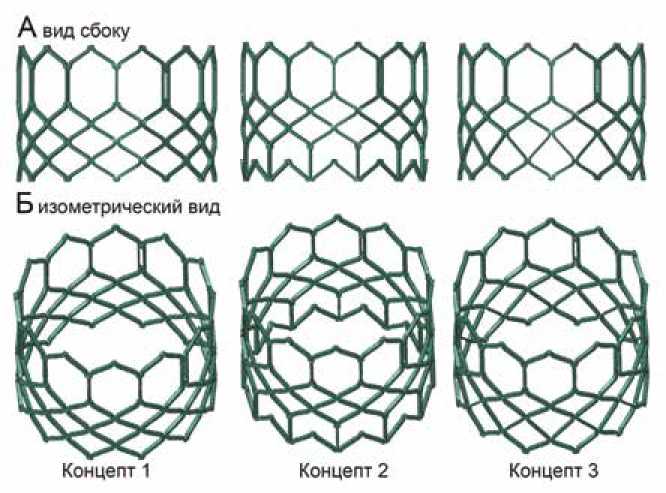
Рис. 1. Трехмерные модели концептов опорных каркасов протеза для исследования в численной постановке. Модели представлены в разных проекциях в итоговом (рабочем состоянии)

Fig. 1. Three-dimensional models of prosthetic support frame concepts for numerical study. The models are presented in different projections in the final (working) state

Для реализации численного исследования на основании всех моделей в среде инженерного анализа Abaqus/ CAE (Dassault Systemes, Франция) встроенными средствами строили сетку конечных элементов из 84–94 тыс. элементов типа C3D8 (139–154 тыс. узлов). При этом особый акцент был сделан на достаточную детализацию модели по толщине – все модели имели три слоя конечных элементов, чтобы обеспечить стабильность расчета при больших деформациях (рис. 2). В рамках моделирования исследовали поведение концептов в двух ключевых тестах-нагрузках, которым подвержен опорный каркас протеза:

• 1.    Этап сжатия, т. е. трансформация каркасов от диаметра хранения 26 мм до имплантационного диаметра 6 мм.

• 2.    Имплантация, т. е. придание рабочего диаметра 26 мм от имплантационного 6 мм.

При этом оба данных этапа реализуются последовательно, именно в описанном порядке. Важнейшим аспектом анализа подобных преобразований диаметров протеза является сохранение последовательности трансформации деформированного состояния и передача всего напряжения от первого шага до второго.

В качестве модели материала для описания свойств опорных каркасов использовали линейную модель для сплава кобальт-хрома, согласно литературным данным (Е = 233 ГПа, предел прочности 933 МПа) [15]. Учитывая ключевую роль пластической деформации при закреплении рабочего диаметра опорного каркаса, в модель ввели предел пластичности, равный 414 Мпа [15]. Таким образом, материал реализует все элементы своего поведения – эластическую компоненту начального линейного участка нагружения и формирование необратимой (пластической) деформации после превышения напряжением границы в 414 МПа.

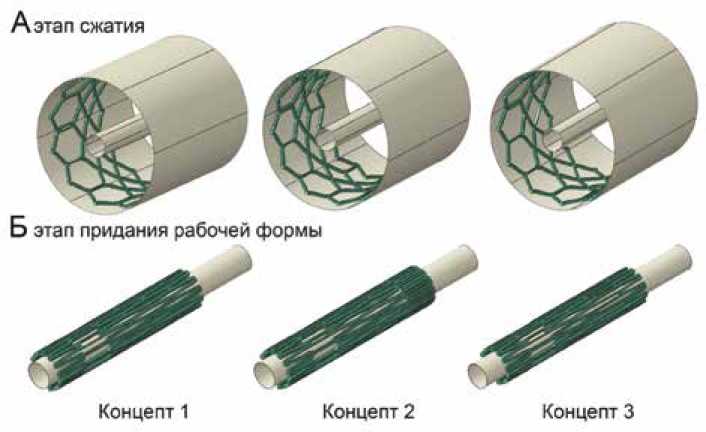
Рис. 2. Постановка численного моделирования для обоих этапов трансформации опорного каркаса: А – визуализация этапа сжатия устройства, Б – этапа придания конечной формы

Fig. 2. Numerical modeling for both stages of transformation of the supporting frame: A – visualization of the crimping of the device, Б – expansion

Исходя из задачи исследования, заключающейся в оценке эффективности и безопасности работы концептов опорных каркасов, в качестве основного количественного показателя для измерения было выбрано напряжение по Мизесу – интегральный критерий прочности, с помощью которого можно определить участки разрушения конструкции и возможность их оптимизации. Пороговым значением для критерия, выше которого происходит повреждение элементов каркаса, является предел прочности, равный для данного материала 933 МПа.

Результаты

Этап сжатия

При исследовании напряженно-деформированного состояния концептов в результате сжатия до предимплан-тационного диаметра показано, что геометрически все конструкции способны изменить свой диаметр до 6 мм. Однако с позиции напряжения по Мизесу концепты 1 и 2 продемонстрировали закритические значения, превышающие порок предела прочности (933 МПа) – 999,6 и 954,0 МПа. Таким образом, стоит ожидать разрушения образцов в некоторых участках (рис. 3, укрупненные виды). При этом концепт 3 обладает значительно меньшими амплитудами напряжения – 865,2 МПа, значения которых меньше пороговых. Соответственно, стоит ожидать, что с позиции прочностного анализа при таком сжатии данный концепт является более перспективным для прикладной задачи. Предположительно, данное отличие обусловлено особенностью центральной зоны каркаса.

Отмечено, что для концептов 1 и 2 максимумы напряжения по Мизесу зафиксированы именно в центральной области (см. рис. 3), наиболее «плотно» заполненной материалом. Ячейки в данной зоне мелкие, в результате сжатия они выраженно деформируются. В концепте 3 существует «удлиненный» ряд, который изменяет свою форму слабее, поэтому и напряжение по Мизесу растет не так значительно.

Придание рабочей формы

Численное моделирование придания рабочей формы в целом продемонстрировало схожие результаты – для концептов 1 и 2 рост напряжения в закритическую область продолжился, достигая 1022,4 и 1044,7 МПа соответственно. Данное поведение вполне ожидаемо, т. к. напряжение, накопленное на первом этапе (сжатие), дополняется новой нагрузкой – расширением стента и повышением амплитуды показателя (рис. 4). Особенно это характерно для областей на стыке ячеек – там, где происходит основной изгиб как при сжатии, так и при расширении конструкции. Данный рост (для максимума) составил 22,8 и 90,7 МПа.

Для концепта 3 подобный эффект также характерен; однако за счет того, что на первом этапе он накопил только 865,2 МПа, дополнительный рост напряжения, составивший 59,0 МПа, не позволил превысить порог прочности даже после этого этапа. Тем не менее итоговая амплитуда достигла 924,2 МПа, чрезвычайно приближаясь к пределу прочности, что свидетельствует о необходимости оптимизации узлов с высокими напряжениями.

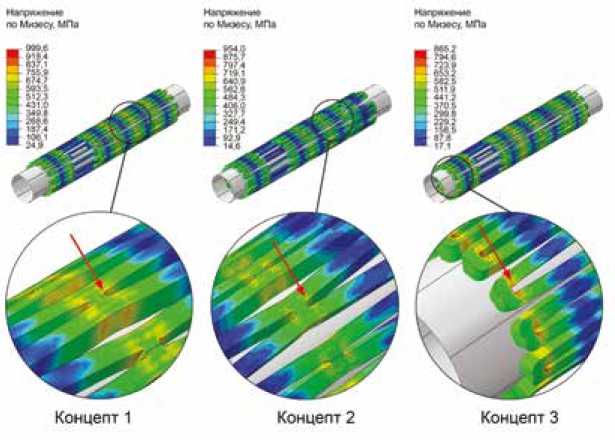
Рис. 3. Эпюры напряжения по Мизесу для трех концептов опорного каркаса с укрупненным видом для этапа сжатия. Стрелками обозначены области с максимальными значениями напряжения

Fig. 3. Von Mises stress plots for three support frame concepts with close-up views for the crimping phase. Arrows indicate areas with maximum voltage values

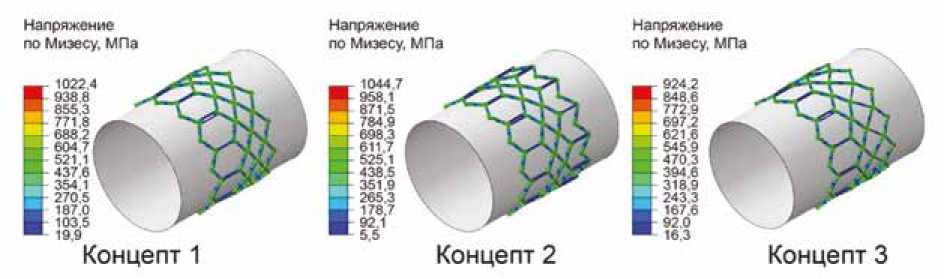
Рис. 4. Эпюры напряжения по Мизесу для концептов опорного каркаса на этапе придания рабочего диаметра Fig. 4. Mises stress diagrams for support frame concepts at the stage of giving the working diameter (expansion)

Обсуждение

Численное моделирование как инструмент разработки изделий широко зарекомендовал себя в медицинском инжиниринге в качестве эффективного и быстрого способа оценки ранних концептов устройства, выбраковки или оптимизации его геометрии. С ростом вычислительных мощностей становится возможным проводить точные достоверные расчеты сложных эффектов и стадий трансформации состояния компонентов или всего изделия целиком, которые происходят на ключевых этапах его функционирования [6]. При этом подобный анализ обладает ключевым преимуществом, недоступным для натурных методов, – возможностью количественно оценить внутренние силы, возникающие в материале, и сравнить их с пороговыми значениями [7–11]. Прежде всего, речь идет о напряженно-деформированном состоянии и критериях прочности.

Настоящее исследование является наглядным примером такого комплексного количественного анализа с оценкой проблемных узлов, рисков безопасности и определением потенциала оптимизации для ключевого компонента медицинского изделия – каркаса транскатетерного протеза клапана аорты. Благодаря такой оценке уже на ранних этапах разработки возможно отказаться или существенно модифицировать концепты, чтобы избежать неудачи на этапе натурного прототипирования образцов [16, 17]. По нашим данным, два из трех представленных вариантов опорных каркасов разрушатся в ходе эксплуатации, а, значит, могут быть исключены из дальнейших работ. Представленный численный анализ значительно быстрее выбраковывает концепты, чем традиционный подход «прототип – тестирование – оптимизация»; он позволяет сократить сроки и стоимость разработки, повысить вероятность успешного ее осуществления и внедрения в производство.

Исходя из вышеуказанных преимуществ, ряд коллективов исследователей-разработчиков активно применяют численное моделирование для схожих устройств – баллонорасширяемых TAVR. В схожей работе M. Bianchi и соавт. (2016) описывают анализ напряженно-деформированного состояния транскатетерного протеза Sapien (Edwards Lifesciences, США) [18]. Несмотря на то, что ими были получены более низкие амплитуды напряжения по Мизесу, чем в нашем исследовании (максимум составил 668 Мпа), в целом картина распределения и характер поведения наших концептов полностью согласуется с представленной работой. Подобное различие может быть обусловлено собственной моделью материала – нержавеющей сталью [19]. Кроме того, некоторые настройки, выбранная погрешность точности моделирования – все это может оказывать умеренное влияние на количественные показатели исследования.

Анализируя результаты настоящего исследования, стоит отметить, что концепты 1 и 2 представляются бесперспективными с позиции прикладной разработки. Напряжение по Мизесу, значительно превышающее порог разрушения, предположительно, не может быть существенно скорректировано за счет оптимизации геометрии. Усилия по снижению данного показателя целесообразно направить на более состоятельный концепт 3, для которого амплитуды максимума напряжения значительно ниже, однако близки к пределу прочности. Выявленные критические области, представленные на эпюрах напряжения, требуют изменения геометрии для создания более безопасного, надежного опорного каркаса. После этого возможен переход к серии прототипов и к натурным испытаниям.

Заключение

Серия численных экспериментов демонстрирует валидность примененного метода – напряженно-деформированное состояние клинических моделей протезов находится в пределах допустимых значений. Их опорные каркасы способны изменять свой диаметр без разрушения и значимых дефектов от 26 до 6 мм и обратно. Показана частичная состоятельность собственного экспериментального концепта баллонорасширяемого опорного каркаса с позиции прочностного анализа. Однако данная модель требует оптимизации геометрии приточной зоны – для уменьшения максимальной амплитуды напряжения по Мизесу ниже предела прочности материала. Продемонстрированная серия численных экспериментов может быть использована в качестве ценного инструмента для исследования и оптимизации стентоподобных конструкций на ранних этапах проектирования, в т. ч. и для выбора перспективных инженерных решений.