Численная модель течения в выхлопном узле «отверстие - колено»

Системы вентиляции, проектируемые в зданиях различного назначения обычно сильно разветвлены, поэтому потери давления на местных сопротивлениях доминируют и в свою очередь являются результатом деформации потока в самих фасонных элементах и при срыве потока с их острых кромок и вихреобразования. Имеется большое разнообразие фасонных элементов, их конструктивных исполнений и комбинаций. Для отвода воздуха от вытяжных устройств – решеток, отсосов, из-за сложности размещения обычно используется комбинация фасонных элементов – колен и отводов, расположенных на небольшом удалении, друг от друга. Так, например, часто встречается вариант установки колена сразу за вытяжной решеткой по ходу движения воздуха. Ясно, что, в таком случае фасонные элементы оказывают влияние друг на друга. Такое взаимное влияние выражается как в изменении коэффициентов местного сопротивления, так и в очертаниях вихревых зон, что на сегодняшний день редко учитывается как при выполнении аэродинамического расчета, так и при конструировании усовершенствованных узлов из профилированных фасонных элементов. Это, в свою очередь, может привести к неточностям расчета и снижению эффективности системы.

Потери давления на преодоление местных сопротивлений в фасонных элементах систем вентиляции и кондиционирования, по разным оценкам, составляют от 40% и более общих потерь давления [1]. При выполнении аэродинамического расчета обычно потери давления на местных сопротивлениях вычисляются путем суммирования по участкам коэффициентов местного сопротивления (КМС) по данным справочной литературы, где, в основном, приведены значения КМС для отдельно стоящих фасонных элементов, то есть при таких расстояниях между ними, что их взаимное влияние исключается. К примеру, в справочнике Идельчика [2] показано, что для выравнивания потока необходим прямой участок не менее 20 калибров. Однако для сетей воздуховодов, имеющих значительные размеры поперечного сечения, характерно близкое размещение фасонных элементов. Поэтому поток не успевает выровняться после деформации в первом, по ходу течения, фасонном элементе, и входит во второй, что существенно искажает картину течения в нем и, соответственно, КМС и очертания вихревых зон.

Существующие экспериментальные, численные и аналитические исследования, обычно рассматривают течение в различных одиночных фасонных элементах и варианты снижения потерь в них. Часть из них посвящена исследованию вихревых зон и возможным вариантам снижения потерь давления за счет профилирования стенок фасонных элементов.

Численные исследования в последнее время проводятся с использованием методов вычислительной гидродинамики (CFD) в программных комплексах. Например, одним из широко используемых инструментов CFD для изучения течений в системах вентиляции и кондиционирования является программный комплекс Ansys Fluent [3]. При численном исследовании правильность установки граничных условий, используемых моделей определяет корректность получаемых результатов. Проведен обзор существующих вариантов моделей турбулентности для исследования рудничной системы вентиляции [4] и для течения в фасонных элементах систем вентиляции при разных числах Ренольдса [5], [6]. Сделаны выводы, к примеру о том, что для простых турбулентных течений применима стандартная k- ε модель, а при наличии течений с сильными завихрениями рекомендуется модель RSM. Однако в ряде работ по исследованию течений, например в прямом отводе [7] и тройнике [8], без какого-либо предварительного обоснования выбрана стандартная k- ε модель.

Одним из редких примеров исследования узлов, состоящих из нескольких фасонных элементов, является работа [9], где была проведена валидация численной модели течения в одинарном и Z-образном отводе. Показано, как размер ячеек влияет на итоговые результаты. Ожидается, что измельчение сетки, особенно в пристеночном пограничном слое, влияет на отличие численных результатов от эксперимента. Рассмотрено 2 варианта моделей турбулентности: realizable k- ε и k-ω sst. В качестве контрольного параметра выбрана потеря давления в сечениях, значения которых сравнивались при разной степени измельчения сетки. Для решения дальнейших задач в модели realizable k- ε выбран средний размер сетки (y*=1.3), в модели k-ω sst результаты практически не зависят от степени измельчения сетки (отличие не более 0.2%). Размер ячейки одинаково влияет на результаты, полученные для одинарного и Z-образного колена. В работе указано, что не удалось найти подходящую модель для правильного расчета течения, и, кроме того, не определены КМС и очертания вихревых зон. В работе [10] представлена верификация численного исследования течений в прямом канале, одинарном колене, U-образном колене и узле, состоящем из нескольких фасонных элементов. Опираясь на сравнения результатов, представленных, к примеру, в исследованиях [11] и [12] выбрана модель k- ε. Полученные потери давления в узлах имеют отклонения от известных результатов от 6.8 до 18.3%. В работах [13] и [14] изучается влияние моделей турбулентности при исследовании течений в отводе одинарном, Z-образном и U-образном. В результате сделан вывод о том, что модель RSM дает более точные результаты, чем модель k- ε.

Актуальным направлением исследования течений в фасонных элементах является разработка усовершенствованных конструкций, имеющих сниженное аэродинамическое сопротивление (КМС). Для снижения КМС используются различные способы – скругление стенок, установка направляющих лопаток [15], [16], которые, например, в случае приточных отверстий уменьшают их влияние друг на друга [17]. Широко рассмотрены варианты снижения КМС в отводах, крестовинах [18], тройниках [19]. Одним из способов снижения КМС в фасонных деталях Kareeva, J.; Chukhlova, M.; Ziganshin, A.; Logachev, K.; Tussupova, K.

Numerical model of the flow in the exhaust unit “opening – elbow”;

систем вентиляции исследователи рассматривают профилирование по очертаниям вихревых зон; по кривым [20], найденным при помощи методов топологической оптимизации или с использованием биомиметики, когда конструкция фасонных элементов выполняется подобной, к примеру, руслам рек [21] или стеблям растений [22].

Характер изменения структуры потока и взаимное влияние местных сопротивлений изучены лишь для ограниченных комбинаций фасонных элементов, к примеру, таких как Z-образные [23], [24] и U-образные отводы [25], [26]. Вместе с тем на практике часто встречаются сильно разветвленные вентиляционные системы и пылегазопроводы, с большим количеством элементов, находящихся близко друг к другу [27], [28]. Поэтому для корректного проведения аэродинамического расчета и определения возможностей профилирования по очертаниям ВЗ актуальны исследования по определению закономерностей для КМС и очертаний вихревых зон в условиях взаимного влияния в узлах вентиляционных систем, в том числе в узле типа «вытяжное отверстие – колено». При численных исследованиях на первом этапе необходимо провести изучение «сеточной зависимости», а также проверку получаемых результатов на предмет физической адекватности и согласованности с известными и достоверными данными.

Поэтому целью исследования является верификация и валидация основных характеристик течения в узле «вытяжное отверстие – колено» – коэффициента местного сопротивления и очертаний вихревых зон. Объектом исследования является узел «вытяжное отверстие - колено».

Для достижения цели исследования необходимо решить следующие задачи:

• -    смоделировать тестовую задачу о течении к вытяжному отверстию без колена, определить влияние обычно использующегося граничного условия «ось симметрии» на результаты;

• -    провести верификацию и валидацию численной модели течения в узле «вытяжное отверстие – колено» - определение «сеточной зависимости» и соответствия с известными данными значений КМС и очертаний ВЗ.

• 2    Materials and Methods

В работе исследуется узел вентиляционной системы, состоящий из колена и вытяжного отверстия, которое расположено на расстоянии l от колена. В препроцессоре Gambit была построена геометрическая модель. Размеры области представлены на рисунке 1. Ширина воздуховода b = 0.1 м, расстояние до колена l = 2 м. Размеры расчетной области L = 2 м, H = 1 м. Вертикальная часть воздуховода после поворота в колене выбрана длиной L1 = 2 м, чтобы корректно рассчитать КМС и обеспечить корректное формирование течения и вихревой зоны (рис. 1).

Численные исследования проводятся с помощью программного комплекса ANSYS Fluent. Граничные условия (ГУ):

• •      AB – ГУ «velocity inlet» - скорость постоянная и направлена по нормали к границе: u 0 = const,

k = 1, ε = 1

• •      AG , GE , DC , CB – ГУ « wall » - (непроницаемые стенки): v = 0, d u n /d n =0; (d n - нормаль к

границе).

• •       FO , OI , IK , KM , MN - ГУ « pressure inlet » (свободная граница), gauge total pressure -

• избыточное давление ΔP=0 Па. Для данного варианта ГУ присутствует возможность задания пары турбулентных параметров в виде: интенсивности турбулентности (Turbulence Intensity, %) и масштаба длины (Length Scale, м); отношения турбулентной вязкости (Turbulent Viscosity Ratio); интенсивности турбулентности и гидравлического диаметра (Hydraulic Diameter, м), и величин k и ε. При выборе пары k и ε по умолчанию их значения стоят равными 1. Но так как на этих границах моделируется подтекание из неограниченного пространства, величины k и ε устанавливаются равными 0.1, что соответствует минимальным турбулентными возмущениям.

а)                                                     б)

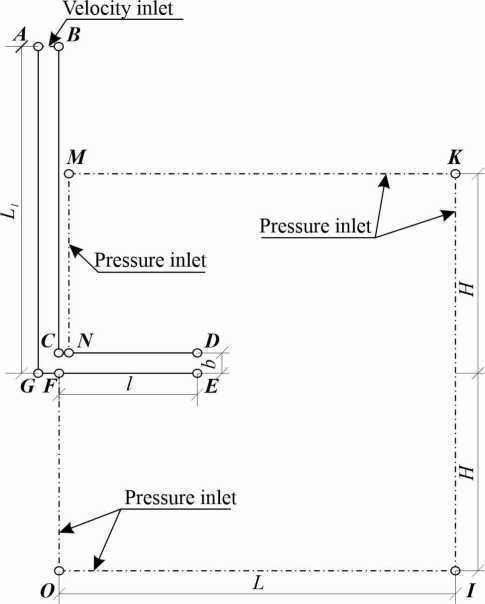
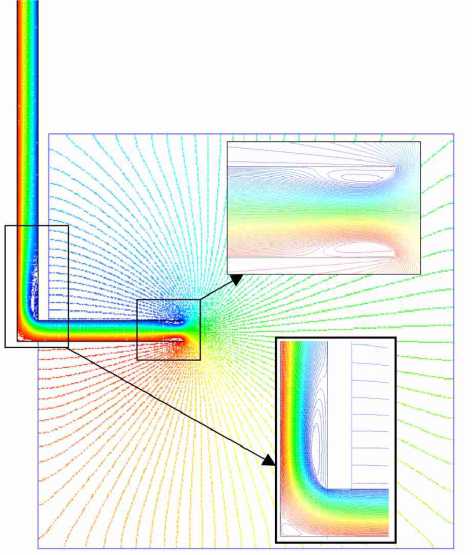
Рис. 1. - Расчетная область: а) геометрия области, б) линии тока течения (Изображение выполнено автором статьи)

Fig. 1 - Computational area: a) geometry of the area, b) flow streamlines (illustration by the authors)

Основываясь на проведенных ранее исследованиях [29], используется модель турбулентности Reynolds Stress (RSM) в комбинации с расширенным пристеночным моделированием - Enhanced Wall Treatment (EWT).

Для верификации численной модели выбрано исследование авторов [29], где исследуется течение к вытяжному щелевому отверстию в торце канала в симметричной постановке. При наличии колена решать задачу в симметричной постановке невозможно, и поэтому на первом этапе исследования, для определения влияния граничного условия «ось симметрии», задача о течении к отсосу без колена решается не для одной половины, а для всей расчетной области. Эта задача соответствует случаю l = ∞ (рисунок 1 а ). Далее решается задача для случая l/b =20. Ожидается, что при данном соотношении l/b можно влиянием колена на вытяжное отверстие пренебречь и рассматривать узел, состоящий из двух отдельных элементов – свободно расположенного щелевого отсоса и колена. Это позволит провести валидацию – изучить и сравнить их характеристики с уже известными данными. Для задачи с отсосом без колена принята скорость u 0 = 10м/с, а для варианта с коленом u 0 = 50м/с, что позволяет получить более стабильную сходимость итерационного процесса. При этом в обоих случаях число Re существенно выше 1·10⁴, что обычно считается развитым турбулентным режимом, а значит можно ожидать автомодельности течения и независимости КМС и очертаний ВЗ от режима течения.

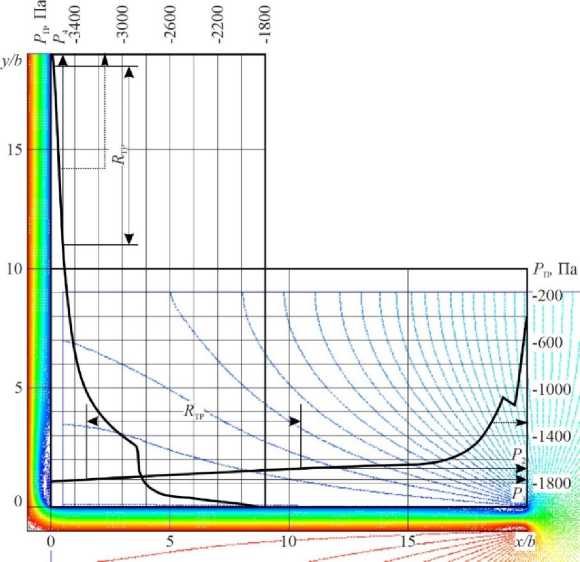
Рис. 2 - Распределение давления (Изображение выполнено автором статьи)

Fig. 2 - Distribution of pressure (illustration by the authors)

Для проверки корректности моделирования узла «вытяжное отверстие - колено» определяются коэффициенты местного сопротивления отдельно вытяжного отверстия и колена, входящие в узел с l/b =20. Для этого по результатам численного решения строится изменение полного давления (осредненного в поперечных сечениях) по длине каналов после входа в вытяжное отверстие и после поворота в колене (рис. 2). Здесь видно, что на прямых участках воздуховода присутствуют зоны, где полное давление изменяется линейно, то есть в этих местах давление падает только под действием силы трения. На этих участках с неопределенностью в 5% определяются значения удельного падения давления путем среднеарифметического осреднения ( R тр – 1.5< x/b< 10.5; 11< y/b< 18.5). Используя эти значения и длины соответствующих участков, вычисляются потери давления на трение на них: ∆ P тр = R тр · l . Длины l для каждого фасонного элемента принимаются равными длинам участков между соответствующими сечениями, в которых определяются давления P 1 , P 2 для вытяжного отверстия и P 3 , P 4 для колена.

Вне областей с линейным падением давления его изменение резко нелинейное и связано с деформацией потока: на участке 10.5< x/b< 20 – из-за влияния входа в вытяжное отверстие, на участке 0< x/b< 1.5 – из-за влияния колена вверх по течению, на участке 0< y/b< 11 – из-за влияния колена вниз по течению и на участке 18.5< y/b< 19 – из-за влияния граничного условия на выходе из канала ( AB ) . Поскольку между участком влияния колена вверх по течению и участком влияния входа в отсос имеется протяженный участок с линейным падением давления, можно считать, что взаимное влияние одного элемента на другой отсутствует. КМС определяется отдельно для каждого элемента: по формуле (1) – для вытяжного отверстия:

P 1 - P 2 -∆ P тр (ρ u 0² / 2)

и по формуле (2) – для колена:

P 3 - P 4 -∆ P тр

(Pu0 /2)   , где P i = 0 - давление на удалении от всасывающего отверстия, Па; Р2 - давление в конце участка влияния входа в вытяжное отверстие (х/b =10.5), Па (рис. 2), △ Pтр - потери давления на прямых участках воздуховода; Рз - давление в начале участка влияния колена (х/b =1.5), Па, P4 -давление на расстоянии у/b =12.

• 3    Results and Discussion

Для определения влияния граничного условия «ось симметрии» и моделей на очертания вихревых зон и значение КМС, были решены задачи для полной расчетной области для вытяжного отверстия без колена. Результаты сравниваются с очертаниями ВЗ, приведенными для симметричной половины течения [29], и значения КМС с известными данными справочника [2]. Из рис. 3 (линии для случая l/b = ∞) видно, что очертания вихревых зон, найденные при помощи разного сочетания моделей турбулентности и пристеночных функций, существенно различаются. Использование обоих сочетаний «стандартной» k-ε модели турбулентности (SKE) с двумя вариантами пристеночного моделирования – стандартных пристеночных функций (SWF) и расширенного пристеночного моделирования (EWT) приводит к существенно меньшим по размерам очертаниям вихревой зоны (рис. 3а). Использование модели «Рейнольдсовых напряжений» (RSM) показывает очертания, размеры которых гораздо ближе к ранее известным результатам, причем очертание, полученное с использованием сочетания RSM EWT, практически совпадает с ранее проведенными численными исследованиями для симметричной половины и имеет достаточно хорошее соглашение с очертанием, найденным экспериментально и методом дискретных вихрей [29]. Значения КМС, найденные в этих задачах, отличаются не более чем на 2%. Поэтому далее для данного исследования будут использовано сочетание RSM EWT.

Далее анализ задачи с расстоянием от входного отверстия до колена l/b =20 (рис. 3а), показывает, что очертания ВЗ1 на входе в отверстие (синяя сплошная линия) полностью совпадают с очертаниями, найденными для задачи без колена (как рассчитанной в этом исследовании для полной геометрии, так и, взятой из более ранней работы [20]), а длина вихревой зоны на 10% меньше, чем для задачи без колена (при l/b=∞), что можно объяснить погрешностями численного эксперимента и расчетной сетки. Вихревая зона после поворота (ВЗ2) также имеет удовлетворительное согласие по форме и по длине (отличие <6%) от вихревой зоны, полученной у одиночного колена в работе [30]. Отличие можно объяснить выбором в расчете другой модели турбулентности, чем в [30].

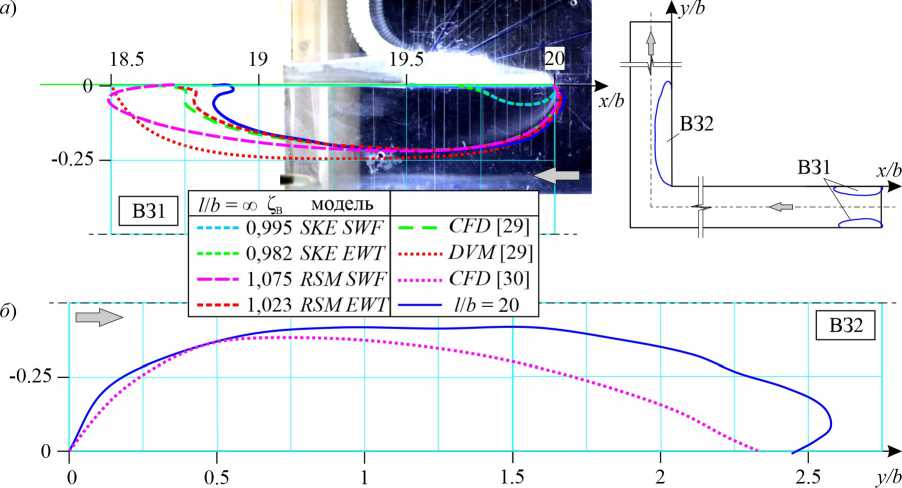
Рис.3 - Очертания вихревых зон: а) первая ВЗ; б) вторая ВЗ (Изображение выполнено автором статьи)

Fig.3 - Outline of vortex zones a) first VZ: b) second VZ (illustration by the authors)

В таблице 2 представлены значения КМС узла (с вычетом трения), полученные по результатам численного исследования; КМС узла по экспериментальным данным [2]; сумма КМС одиночного колена (ζК) [30] и вытяжного отверстия (ζВ) [29], которые определены в результате численного моделирования.

Таблица 1. Значения коэффициента местного сопротивления узлов

Table 1. The values of the local drag coefficient of units

Источник	ζ В	ζ К	Σζ
Эксперимент [2]	1	0.79	1.79
Численный расчет – отдельные элементы [29], [30]	1	1.05	2.05
Численный расчет l / b = 20	1.03	1.05	2.08

Здесь видно, что разработанная компьютерная модель хорошо согласуется как с экспериментальными данными (отличие около 15% при l/b = 20), так и с численными исследованиями (отличие около 1.5%).

• 4    Conclusions

В результате исследования получено:

• 1.    Влияние граничного условия «ось симметрии» на полученные результаты отсутствует, что позволяет рассчитывать задачу в полной области, для несимметричных случаев.

• 2.    Результаты, полученные при использовании модели турбулентности RSM и расширенных пристеночных функций, хорошо согласуются с известными экспериментальными данными.

• 3.    Фасонные элементы, находящиеся в узле на расстояниях l / b = 20 и более, можно рассматривать как отдельные.

Дальнейшие исследования при использовании выбранной модели численного исследования будут направлены на изучение влияния расстояния от вытяжного отверстия до колена на такие характеристики течения у вытяжного отверстия, как очертания вихревых зон, коэффициент местного сопротивления узла, с построением по результатам исследований основных зависимостей, необходимых для инженерных расчетов и конструирования усовершенствованных профилированных конструкций узла.