Численная оценка качества учебных on-line курсов

С организацией (самоорганизацией) реально – виртуальной образовательной среды и как следствие с появлением on-line курсов изменились роли всех участников образовательного процесса. При этом педагог превратился в руководителя, студент в самостоятельного обучающегося, а компьютер в инструмент коммуникации, обеспечивающий «искусственный интеллект», вычислительную работу, интерактивность и мониторинг за процессом подготовки студента.

В то же время, потребность в относительно дешевой и эффективной массовой подготовке кадров в реально-виртуальной среде породило множество специфичных и трудно структурированных и формализуемых педагогических проблем. На практике стало очевидно, что эти проблемы можно разрешить только в интеграции педагогических, психологических и инженерных методов. В результате сформировалась новая методология с названием дидактическая инженерия [1, 2], нацеленная на эффективную организацию деятельности всех участников образовательного процесса в реально-виртуальной среде.

Следует отметить, что все проблемы в предложенной классификации Г.Саймоном, подразделяются на три класса:

• 1)    хорошо структурированные или количественно сформулированные проблемы, в которых существенные зависимости выяснены настолько хорошо, что они могут быть выражены в числах или символах, получающих, в конце концов, численные оценки;

• 2)    неструктуризованные или качественно выраженные проблемы, содержащие лишь описание важнейших ресурсов, признаков и характеристик, количественные зависимости между которыми совершенно неизвестны;

• 3)    слабоструктуризованные или смешанные проблемы, которые содержат как качественные, так и количественные элементы, причем качественные, малоизвестные и неопределенные стороны проблем имеют тенденцию доминировать.

Для решения неструктурированных проблем куда и относятся многие педагогические, используются методы экспертных оценок, т.е. когда математическая формализация проблемы затруднена в силу их новизны и сложности, либо требует больших затрат средств и времени.

Общим подходом для всех методов экспертных оценок является обращение к опыту экспертов, на основе которых зарождаются в определенной степени формализованные методы и алгоритмы, позволяющие автоматизировать процесс принятие решений с использованием вычислительной техники.

В работе рассматривается случай, когда учебный курс представляет собой сложную замкнутую информационную систему, нацеленную и предназначенную для освоения какой-то компетенции. При этом очевидно, что разные курсы в зависимости от их качества организации, содержания, формы, сложности обладают разным обучающим потенциалом (в смысле возможностями) для освоения требуемой компетенции.

В этой ситуации актуализируется необходимость разрешения следующей проблемы.

Требуется до начала эксплуатации рассматриваемого экземпляра on-line курса оценить его обучающий потенциал, т.е. его качество с точки зрения достижения цели (освоение компетенций) через обучение.

Разумеется, обучающий потенциал on-line курса, как любой сложной системы, зависит от потенциала его подсистем. В свою очередь, потенциал любой подсистемы зависит от множества скрытых (латентных) и расчетных (метрических) показателей этих подсистем.

Очевидно, что на практике, оценить значение скрытых показателей может только эксперт, например, такие показатели как валидность и релевантность вопросов теста. Что касается расчетных показателей, то их значением метрик, также можно оценить, исходя из данных трудозатрат экспертов, например, сложность теста можно оценить по продолжительности ответов на них эксперта, продолжительность процесса тестирования для студента можно вычислить, исходя из значения показателя сложности теста [1, 2] и т.д.

Структурная модель организации содержания on-line курса

В общем случае, независимо от формата организации учебного процесса [3, 4], структурная модель on-line курса (УОК) может быть представлена в виде графа (рис.1).

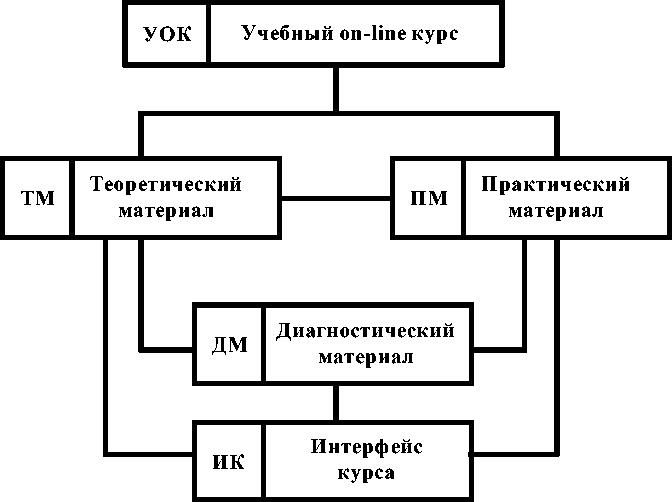
Рис. 1. Структурная модель организации УОК

Согласно рис. 1, в УОК выделены четыре взаимосвязанных подсистемы: ТМ, ПМ, ДМ, ИК.

При вычислении значения показателя качества УОК, с учетом качества всех его подсистем, изначально используется принцип пропорциональных влияний, т.е. каждая подсистема с весом пропорционально своему качеству влияет на образование качества УОК в целом. На концептуальном уровне эту зависимость показателя качества УОК от показателей качества ее компонент ТМ, ПМ, ДМ и ИК можно записать как функциональную зависимость, т.е.

УОК = F(TM, ПМ, ДМ, ИК).

В модели также вводятся нормировочные ограничения: значения показателей качества Q(УОК), Q(TM), Q(nM), Q(ДМ), Q(ИК), изменяются почти от 0 до 1, т.е. в интервале за исключением нуля (0, 1). Таким образом, у идеального экземпляра УОК, т.е. у курса наивысшего качества будут все значения показателей равными 1 или имеют 100% значение показателя качества. Формально, в наших условиях и обозначениях, можно записать так

Q(УОК) = 1 = F(1, 1, 1, 1).

Аналогично, любые значения показателей качества подсистем: ТМ, ПМ, ДМ, ИК могут быть детализованы на следующем иерархическом уровне со своими показательными параметрами, т.е. t(*), n(*), g(*), u(*). Сами подсистемы (аналогично системе) могут быть представлены так

ТМ = F1(t(1), ..., t(*), ..., t(k1))

ПМ = F2(n(1), ..., n(*), ..., n(k2))

ДМ = F3(g(1), ..., g(*), ..., g(k3))

ИК = F4(u(1), ..., u(*), .„, u(k4)), где значения показателей качества компонент Q(t(*)), Q(n(*)), Q(g(*)), Q(u(*)) подчиняются ограничению (0, 1).

Следует отметить, что эту декомпозицию метрических оценок качества подсистем можно продолжить до практически необходимого уровня детализации. При этом, на любом иерархическом уровне организации оценки качества, значения показателей этого качества изменяются в пределах (0, 1].

Среднее геометрическое как метрика показателя качества УОК

Всем принятым в модели ограничениям удовлетворяет функция «среднее геометрическое», т.е. функция вида

Конкретно рассмотрим только двухуровневую модель для оценки качества УОК. В наших обозначениях эта модель выглядит так:

Q(УОК) = ^ТМ * ПМ * ДМ * ИК где k1, k2, k3, k4 - количество характеризующих параметров у подсистем.

Таким образом, оценка качества любого объекта сводится к задаче вычисления среднего геометрического всех узлов сети (рис. 1) с соблюдением иерархии уровней организации.

На практике возникает резонный вопрос: почему надо использовать функцию «среднее геометрическое», а не, например, среднее арифметическое, которое часто употребляется на практике для оценки качества объекта. Приведем пример: допустим качество какой - то системы СИ зависит от ее составляющих С и И. При этом известно, что качество С = 0,9, а качество И = 0,1. По принятому правилу расчета качество СИ (по среднему геометрическому) равно 0,3, а по среднему арифметическому 0,5. Таким образом, среднее геометрическое улавливает эффект слабого звена (эффект - «где тонко, там и рвется»), т.е. среднее геометрическое «умеет» ловить системы с низким качеством одного из составляющих компонент и отражать пропорционально его влияние на оценке качества всей системы. В целом это и понятно, элемент с очень низким качеством в системе «делает» всю систему пропорционально себе с низким качеством. Очевидно, такая оценка качества системы оказывается более валидной (адекватной) на практике в реальной ситуации.

Пример оценки качества УОК

Для того, чтобы оценить качество УОК в целом, необходимо оценить качество его компонент: ТМ - теоретического материала, ПМ - практического материала, ДМ - дидактического материала, ИК - интерфейса курса. Следует подчеркнуть, что интерфейс рассматривается как внешнее представление интерактивной автоматизированной подсистемы управления курсом.

Качество теоретического материала оценивается экспертами по следующим трем критериальным компонентам:

Q(TSP) – качество соответствия теоретического материала программе (изменяется почти от 0 до 1).

Q(TZR) – качество соответствия теоретического материала обучению студента в «зоне ближайшего развития» (изменяется почти от 0 до 1).

Следует подчеркнуть, что учебный материал, который обеспечивает дальнейшее развитие способностей студента, является доступным, только тогда, когда он из «зоны ближайшего развития» этого студента.

Q(TSP) – качество соответствия теоретического материала обучению «на высоком уровне трудности». (изменяется почти от 0 до 1).

Обучение «на высоком уровне трудности» обеспечивает быстрое развитие способностей студента. Это, в свою очередь, приводит к быстрому освоению им «зоны ближайшего развития» с трансформацией ее в зону развития.

Аналогично, качество практического материала оценивается экспертами, также по трем критериальным компонентам:

Q(ПТМ) – качество соответствия практического материала теоретически изложенному материалу (изменяется почти от 0 до 1).

Q(ПZR) – качество соответствия практического материала обучению в «зоне ближайшего развития» (изменяется почти от 0 до 1).

Q(ПSP) – качество соответствия практического материала обучению «на высоком уровне трудности». (изменяется почти от 0 до 1).

Качество интерфейса как средства, обеспечивающего качества общения обучающегося с УОК восприниматься им как общение (в определенной мере) с «умной» системой. Таким образом, чем «умней» интерфейс системы, тем выше качество «общения» с системой. Качество интерфейса УОК оценивается экспертами по четырем критериальным компонентам:

Q(ИСТ) – качество «сервиса» организации работы с теоретическими материалами курса (изменяется почти от 0 до 1).

Q(ИСП) – качество «сервиса» организации работы с практическими материалами курса (изменяется почти от 0 до 1).

Q(ИСР) – качество «сервиса» организации документирования данных по результатам работы (изменяется почти от 0 до 1).

Q(ИСК) – качество «сервиса» организации аналитической и коррекционной работы на основе данных обратной связи (изменяется почти от 0 до 1).

Особо подчеркнем, что, качество всех критериальных компонент УОК на любом иерархическом уровне организации оценивается по одному и тому же рекурсивному алгоритму, поэтому вполне достаточно подробно привести расчет значения показателя качества одной из компонент, например, ДМ, а качество других компонент УОК, т.е. ТМ, ПМ, ИК будет оцениваться аналогично ДМ.

Согласно разработанной модели качество ДМ будет оценено по формуле

В этой формуле приняты обозначения: Q(VAL) – качество валидности (адекватности, корректности и пригодности) комплекса вопросов, предложенных студенту в тесте; Q(REL) – качество релевантности вопросов теста, т.е. спрашивается ли в них то, что изложено в рамках курса; Q(REP) – качество репрезентативности вопросов теста, т.е. равным ли образом представлены вопросы в тесте из всех разделов курса, проверяемых на актуальный момент; Q(KSM) – качество полноты и целостности комплекса вопросов, т.е. представлены ли в тесте одинаковое количество вопросов на знание «фактов» и на знание «связей» в изучаемой предметной области в рамках курса. На практике, оценку качества теста по критериям VAL, REL, REP, KSM могут оценить только эксперты в процессе исследования предложенного экземпляра УОК.

Алгоритм оценки качества ДМ

Допустим, качество ДМ как подсистемы УОК, оценивают шесть экспертов независимо друг от друга. Результаты представлены на рис. 2.

Эксперты Критерии	1	2	3	4	5	6	Среднее значение
VAL	0,9	0,8	0,6	0,9	0,7	0,9	0,8
REL	0,8	0,7	0,8	0,7	0,7	1	0,783
REP	0,8	0,7	0,7	0,8	0,8	1	0,8
KSM	0,7	0,8	0,7	0,6	0,7	1	0,75

Рис. 2. Данные экспертных оценок качества теста учебного курса

По данным (рис. 2) в четырехмерном пространстве качества компоненты ДМ в единичном круге построена диаграмма Кивиата для демонстрации качества дидактического материала по разным критериям (рис. 3).

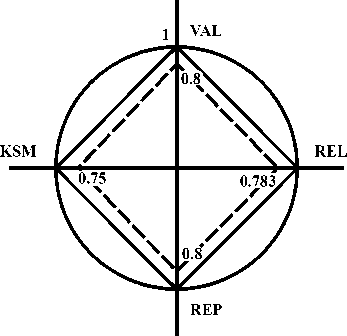
Рис. 3. Диаграмма Кивиата для визуализации состояния качества дидактического материала учебного курса

Согласно модели, интегральную оценку качества ДМ можно вычислить как среднее геометрическое, т.е.

ДМ = F3(VAL , REL , PER , KSM) ; Q ( ДМ ) = 4/0,75 • 0,78 • 0,8 • 0,8 = 0,782 .

К слову сказать, что в рассматриваемом примере значения показателей качества компонент УОК примерно равны, поэтому значение среднего геометрического не будет значимо отличаться от значения среднего арифметического.

Таким образом, значение качество Q(ДМ) в рассматриваемом курсе ровно 78% из 100% возможных. В принятой вузовской шкале, качество подсистемы ДМ оценивается как «отличное». Следует отметить, что результаты работы экспертной группы, полученные в ходе опроса должны пройти обязательную проверку на согласованность. Если мнения экспертов окажутся несогласованными, т.е. мнения существенно отличаются друг от друга внутри группы, то результаты признаются непригодными для вынесения обоснованного решения, например решения: купить или не покупать этот экземпляр УОК для подготовки студентов. Очевидно, при этом сама экспертиза считается с ненадежными результатами.

В этом случае, для лица принимающего решения (ЛПР), возможно три варианта действия:

• 1.    Пригласить новую команду экспертов, так как может быть квалификация экспертов «старой команды» сильно отличается или у кого – то из членов команды есть «побочный» интерес, т.е. оценки, смещены относительно этого интереса и поэтому у них разные критерии оценки качества.

• 2.    В рамках «старой команды» использовать метод Дельфи (авторы этого метода О. Холмер, Т. Гордон, США). Как известно, этот метод позволяет получить согласованные значения оценок в процессе анонимного обмена мнениями между участниками группы экспертов и на базе этих мнений принять решения в зависимости от ситуации. Очевидно, что если ДМ, т.е. диагностический материал, создан вами, то учитывая мнения экспертов можно изменить содержание и переформатировать этот материал и значимо улучшить качество материала.

• 3.    Отказаться в целом от приобретения этого экземпляра УОК в виду сомнительного качества ДМ.

Формализованным общепринятым методом проверки согласованности мнений экспертов является метод, основанный на вычислении коэффициента множественной ранговой корреляции Кендалла – Смита, так называемого коэффициента конкордации с проверкой его статической значимости.

Для проведения процедуры проверки согласованности мнений экспертов, представленные ими данные, ранжируются по следующим правилам: самой высокой оценки присваивается ранг 1, следующей – 2 и т.д. Одинаковым оценкам присваиваются одинаковые ранги, равные среднему арифметическому их порядковых номеров. Такие ранги называются связанными. Сводные таблицы ранжирования представлены на рис. 4.

Эксперты Критерии	1	2	3	4	5	6	∑
VAL	1	1,5	4	1	3	4	14,5
REL	2,5	3,5	1	3	3	2	15
REP	2,5	3,5	2,5	2	1	2	13,5
KSM	4	1,5	2,5	4	3	2	17

Рис. 4. Сводная карта ранговых оценок

Для вычисления коэффициента конкордации воспользуемся известным соотношением nm

K (Кендалла-Смита)

Z ( Z r -r¹

K = -j-------—

• — ( m ²( n' - n ) - m • У T

12                 j^ j где rij- ранг i – ого показателя у j– ого эксперта:

nm

. ZZr

r = -=^:L-^2±—

n где n – число оцениваемых показателей; m – число экспертов в составе группы. Tj=Vj3-Vj где Vj – количество одинаковых связанных рангов, выставленных j – ым экспертом. Используя расчетные соотношения, получим

r = (14,5 + 15 + 13,5 + 17)/4 = 15

T = V ³ - V = (2)³ - 2 = 8 - 2 = 6

T ₂ = [(2)³ - 2] + [(2)³ - 2] = 12

T 3 = [(2)³ - 2] = 6

T 4 = 0

T = (3)³ - 3 = 27 - 3 = 24

T = (3)³ - 3 = 27 - 3 = 24

E T j = 72

j - 1

^(36 • 60 - 6 • 72)

Визуальная оценка значения коэффициента К позволяет предположить, что мнения экспертов не согласованное, т.е. сделать вывод о несогласованности экспертных оценок. Тем не менее, чтобы в этом убедиться, проверим гипотезу 2

согласованности статистики по критерию X ■ Для этого воспользуемся формулой

X

nm

EE (■'

i = 1 j = 1

1                1 m

—⁽ m • n ⁽ n - 1)^-— E T j )

12                  n - 1 j = 1

В рассматриваемом случае

X

6.5

1          72

— (24 • 3 - —)

12          3

= 1,62

Сравним эту величину с табличным значением критерия для уровня значимости ^a = 0,05 степень свободы f= 3; х таб = 7,8 > 1,62. Из этого можно сделать вывод, что мнение экспертов не согласованное, относительно «отличного» качества теста. Разумеется, это снижает надежность оценки теста, т.е. мнение экспертов разошлись, и верить этой оценке сомнительно и в этом случае используем три варианта поведения, предложенное ранее.

Оценка качества УОК

Допустим, в рассматриваемом случае ЛПР использовал метод Дельфи (см. пункт 2) и авторы переделали подсистему ДМ (с точки зрения повышения ее качества), а затем повторно эта подсистема прошли экспертизу с результатом: мнение экспертов согласованное; качество Q(ДМ) = 0,873. Далее, на практике по аналогии с нашими вычислениями, эксперты оценили качество всех компонентов у системы УОК. При

этом получили следующие результаты: Q(ТМ) = 0,613 (мнение согласованное); Q(ПМ) = 0,73 (мнение согласованное); Q(ИК) = 0,66 (мнение согласованное).

Для наглядного представления результатов построим диаграмму Кивиата (рис. 5).

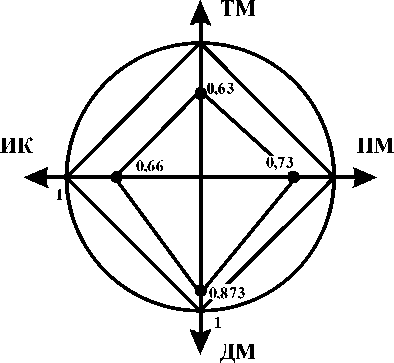
Рис. 5. Диаграмма Кивиата для визуализации состояния качества УОК

В целом, численное значение показатель к ачеств а УОК вычисляется так:

Полученный результат показывает, что качество Q(УОК), т.е. образовательный потенциал учебного on-line курса, примерно, составляет 72% из возможных 100%. По принятой в вузе шкале результат - «удовлетворительный».

Очевидно, что при этом значении показателя качества, ЛПР решает: искать лучший вариант УОК или, в зависимости от ситуации, остановиться на этом.

Разумеется, при использовании на практике описанного метода для принятия обоснованных решений, весь вычислительный процесс, а также логический анализ необходимо формализовать, т.е. построить алгоритм и сетевое программное обеспечение (ПО) для ЛПР.

Системный (численный) анализ качества УОК кафедры

На практике, как правило, on-line курсы бывают, развернуты внутри какой – то популярной оболочки, например, MOODLE. . Очевидно, в рамках одной оболочки отличие в качествах интерфейсов разных курсов становится незначительными. Поэтому, в этих условиях качество экземпляра УОК становится целесообразно оценивать без компоненты ИК. На рисунке 6 приводится структурная модель курса без учета этой компоненты.

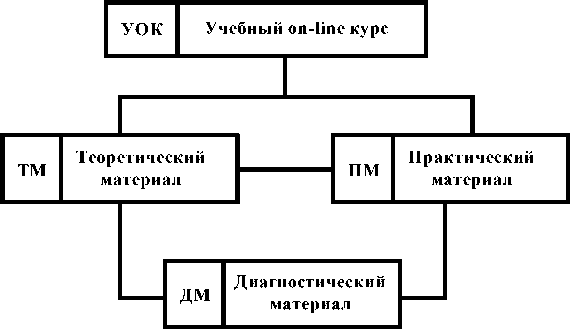
Рис. 6. Структурная модель организации УОК в рамках MOODLE

На кафедре Информатики и прикладной математики (ИПМ) КНИТУ было организована независимая диагностика качества 10 курсов, действующих по направлениям подготовки Информационные системы и технологии (09.03.02, 09.04.02), которые развернуты в MOODLE. Результаты приведены на рисунке 7. Переводная качественная шкала такая – же, как принято в экзаменационных ведомостях, т.е. неудовлетворительно – [0 до 60], удовлетворительно – [61 до 73], хорошо – [74 до 87], отлично – [88 до 100] баллов.

Курсы	Q(ТМ)	Q(ПМ)	Q(ДМ)	Q(УОК)	Оценка
УОК 1	0,81	0,77	0,65	0,74	хорошо
УОК 2	0,87	0,78	0,68	0,77	хорошо
УОК 3	0,78	0,83	0,59	0,73	удовлетворительно
УОК 4	0,92	0,69	0,71	0,77	хорошо
УОК 5	0,88	0,79	0,58	0,74	хорошо
УОК 6	0,71	0,86	0,57	0,70	удовлетворительно
УОК 7	0,75	0,92	0,55	0,72	удовлетворительно
УОК 8	0,77	0,87	0,61	0,74	хорошо
УОК 9	0,69	0,88	0,72	0,76	хорошо
УОК 10	0,66	0,91	0,66	0,73	удовлетворительно
Среднее	0,78	0,83	0,63	0,74	хорошо

Рис. 7. Результаты выборочной диагностики качество УОК по направлениям подготовки 09.03.02, 09.04.02 образовательного пространства ИПМ

Из данных диагностики следует: 1. Значение среднего показателя качества УОК в образовательном пространстве кафедры ИПМ едва дотягивает на оценку «хорошо», т.е. вывод – необходимо повышать качество курсов. 2. Особое внимание необходимо уделять тестам, т.к. их среднее значение показателя качества находится почти на нижней грани оценки «удовлетворительно», т.е. требуется срочно переработать.

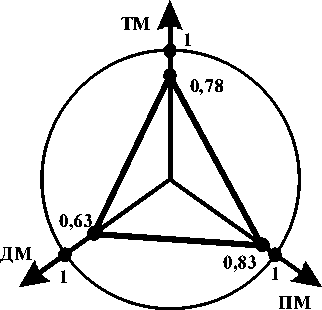
Рис. 8. Диаграмма Кивиата, построенное по средним значениям показателей качества УОК в образовательном пространстве ИПМ

Следует особо подчеркнуть, что метод оценки качества масштабируется на любом иерархическом уровне организации образовательного пространства, можно оценить качество отдельных компонент УОК, в целом УОК, усредненное качество УОК в образовательном пространстве кафедры, факультета, института, университета и т.д. При этом на любом иерархическом уровни организации образовательного пространства выявляются слабые (с точки зрения качества) компоненты этой организации, что позволяет впоследствии целенаправленно их улучшит на любом уровне иерархии этого образовательного пространства.