Численная оценка продолжительности контрольного задания

Любой учебный курс нацелен на освоение какой–то компетенции. При этом студент освоивший компетенцию должен уметь (быть способным), а если на этом и зарабатывает средства, обязан в рамках этой компетенции разрешать проблемы до определенной сложности.

По завершении курса подготовки на практике всегда возникает педагогическая проблема: сколько времени необходимо и достаточно дать студенту для решения учебной проблемы (теста, контрольной работы), чтобы объективно оценить качество владения им компетенцией с учетом его некоторых природных особенностей (медлительность, невнимательность, недостаточная сосредоточенность, волнение, поспешность в критических ситуациях). Как правило (статистика не опровергает), людей с такими особенностями природа часто «сверх нормы» награждает свойством креативности, которая очень необходимо, например, инженеру, ученому и многим другим профессиям, основанных на творчестве. Очевидно, что продолжительность диагностической процедуры оценки качества владения компетенцией должна быть достаточной, но не излишней, т.е. студент за отведенное ему время должен успеть проявить весь свой текущий потенциал при решении контрольных учебных проблем.

Зона развития и продолжительность решения проблемы

Продолжительность времени решения учебной проблемы (теста, контрольной работы) студентом является случайной величиной X и зависит от трех факторов: сложности учебной проблемы (S); от качества (К) владения им компетенцией и природных особенностей студента, т.е. скорости (W) его реакции. Из сказанного следует, что можно записать следующую факторную модель

X = F(S, K, W)

На рис. 1 приводится классы учебных проблем, наиболее часто используемые на практике для оценки качества владения компетенцией.

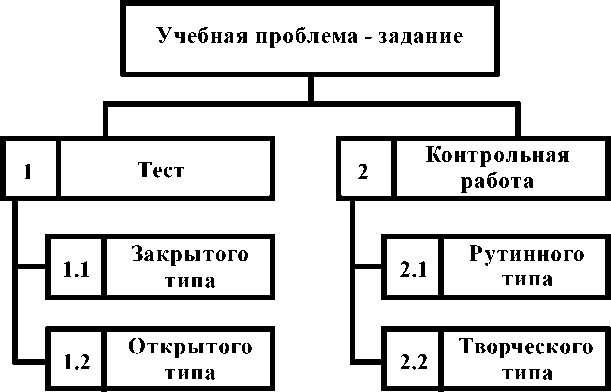
Рис. 1. Учебные проблемы - задания, используемые в диагностике

Студент при проверке качества владения компетенцией, например, при тестировании или выполнении другого задания может находиться в трех состояниях: вопросы задания из зоны его развития (ZR); вопросы задания из «зоны ближайшего развития (ZBR)»; вопросы задания из зоны его дальнейшего развития (ZDR). На рис.

2 перечислены все возможные варианты его состояния.

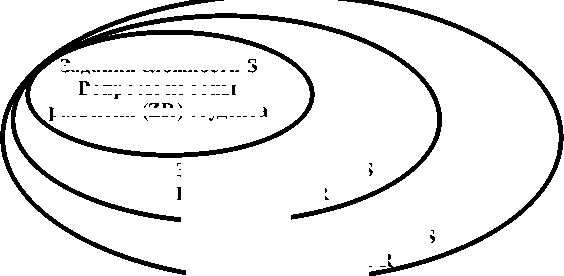
Задания сложности S

Вопросы из зоны развития (ZR) студента

Рис. 2. Три состояния, в которых может находиться студент при выполнении контрольного задания

Задания сложности S

Вопросы из ZBR

Задания сложности S

Вопросы из ZDR

Продолжительность выполнения задания (с момента, когда студент приступил к процессу выполнения задания до момента его окончания, т.е. выхода с процесса) является случайной величиной X. Значения x(1), x(2), x(3),…, x(*) этой величины зависят от сложности задания S, а также, в какой зоне развития находится студент на контролируемый момент времени (рис. 3).

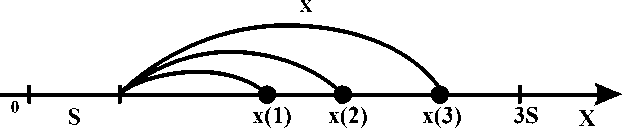
X={x(1), x(2), x(3)„..}

Рис. 3. Возможные значения случайной величины X

На рис. 4. представлены три закона распределения случайной величины X, соответствующие трем состояниям, т.е. ZR, ZBR и ZDR студента при ответе на вопросы задания. Эти графики построены на основе экспериментальных данных, полученных в течение 15 лет с участием 750 студентов [1-3].

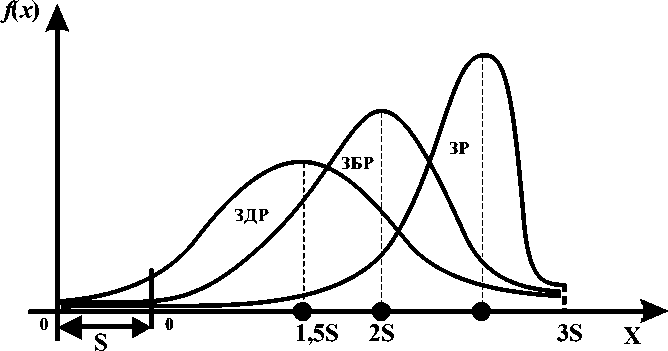
Рис. 4. Законы распределения случайной величины X

Из экспериментальных данных следует, если для студента вопросы задания принадлежат ЗДР, то продолжительность пребывания студента в процессе поиска решения подчиняется нормальному закону распределения, числовые характеристики, которой зависят от зачтения величины S. Таким образом, в этом случае получается «белый шум» с гауссовским законом распределения. Для других случаев закон распределения смещается и требует дополнительного исследования.

Оценки продолжительности теста закрытого типа

Допустим, в качестве задания студенту предложен тест закрытого типа сложности S = s. Построим модель диагностического процесса, представим ее в модели как систему массового обслуживания (СМО). Значения параметров модели будут идентифицированы на основе статистических данных, полученных в реальных условиях подготовки и контроля над успеваемостью студентов.

Сначала опишем вербальную модель ситуации на примере. Допустим, группа студентов (групповой поток) села в автобус, и он поехал по прямой дороге. Каждый из студентов независимо от других решает там свою задачу. Задачи все одинаковой сложности и из одной компетенции, которую они должны были освоить в рамках курса. Как только студент решит задачу, его высаживают из автобуса. Постепенно автобус пустеет, студенты высадились на случайных точках дороги, но в автобусе остаются еще те у которых мизерный шанс решить задачу (низкое качество владения компетенцией). Очевидно, сколько бы не ехал автобус, шансы у оставшихся значимо не растут. Вопрос: где остановить автобус, высадить всех, чтобы, с надежностью 95% гарантировать безрезультатность дальнейшей езды и впустую не тратить бензин?

Теперь построим математическую модель этой задачи, т.е. на базе статистических данных требуется оценить значение величины Т (продолжительность времени тестирования студента). Значение величины Т зависит от значения детерминированной величины S (сложность - трудоемкость теста, которую оценит эксперт) и случайной величины X, где значение случайной величины X равно продолжительности времени реакции студента для ответов на комплекс вопросов теста.

На практике рассмотрим новую случайную величину X1 = T – X, отчитываемую от конца процесса. На основе статистического материала установим закон распределения случайной величины X = X1. Для этого на специально сформированной шкале (рис. 5) отложим продолжительности реакций всех студентов в группе [4, 5].

Рис. 5. Шкала с отметками значений X (продолжительности реакции студента для ответа на вопросы теста)

Для идентификации закона распределения рассмотрим экспериментальные данные, которые сформировались в системе MOODLE в течении 15 лет. В эксперименте участвовало 50 групп. Средняя численность студентов в одной группе 25 человек. Усредненные данные представлены на рис. 6.

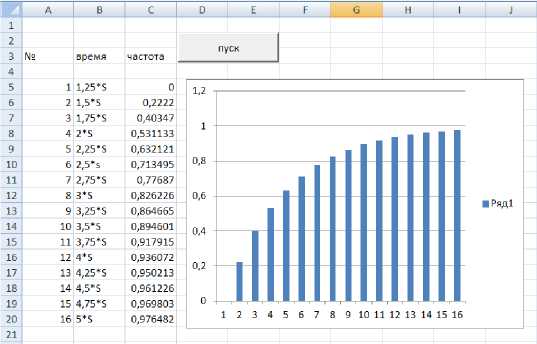
Рис. 6. Результат обработки экспериментальных данных (эмпирический закон распределения величины X)

Согласно данным из графика, частота (эмпирические вероятности) добровольного выхода студента из процесса (процедуры тестирования) будут следующие ( X - случайная величина - время выхода по завершению теста).

P ( X < 1,25*S) = 0, т.е. вероятность, того, что студент завершит тест и выйдет с процесса тестирования раньше, чем 1,25* S равна нулю, где S - сложность теста. P ( X < 1,5* S ) = 0,2222, т.е. вероятность того, что студент завершит тест и выйдет с процесса тестирования раньше чем 1,5* S равна 0,22 (22%).

Аналогично: P ( X <  1,75* S ) = 0,40; P ( X < 2*S)=0,51, т.е. ко времени 2* S , завершив процесс, выйдут четь больше половины студентов и т.д.

Из графика следует, что активное время выхода студентов по завершении теста (продолжительность самообслуживания) начинается с момента времени S и продолжается до момента T - конец тестирования. Исходя из этого, начало координат на графике можно перенести на момент S , т.к. до момента S никто не завершает тестирование. Как следует из частотной характеристики случайной величины X (интегральная характеристика) средняя продолжительность самообслуживания (тестирования) в активной зоне равна величине Т (ср) = 2* S .

Из статистического анализа данных, следует, что при уровне значимости а = 0,05 (гипотеза проверялась по критерию χ2) случайная величина X подчиняется экспоненциальному закону распределения с интенсивностью потока равным X = 1/

Т(ср) = 1/2*S, т.е.

F ( х ) =

1 - e ^{- 1} ,

0,

х >  0

х <  0

Из этого следует, что поток самообслуживающихся студентов может быть описан как модель СМО с групповым одноканальным «выходным» потоком пуассоновского типа.

Из тех же рассмотренных экспериментальных данных известно, что в среднем из группы с 25 студентами, тест на положительную оценку не могут сдать 3,5 студента, и это не зависимо от продолжительности времени Т. В целом, это означает, что в среднем примерно 14% студентов сдают тест на «два». Исходя из этой информации и данных графика, находим, что T = 3,25*S.

Итак, экспериментально доказано, что продолжительность тестирования Т устанавливается по правилам:

• 1.    Эксперты должны оценить S – сложность (трудоемкость в мин/раб) теста.

• 2.    Задать для студентов продолжительность (трудоемкость) тестирования Т = 3,25*S (мин/раб) и провести процедуру тестирования. При этом вероятность ошибки не превышает 5%.

На практике, сложность S (трудоемкость) теста оценивается экспертами через «себя», т.е. оценивается продолжительность времени, которое необходимо эксперту на выполнение теста. Очевидно, что в роли эксперта может выступать опытный преподаватель.

Оценки продолжительности выполнения заданий других типов

Аналогичные расчеты для оценки продолжительности выполнения заданий проведены и для других типов заданий. На рисунке 7 приводятся расчеты продолжительности времени выполнения студентом заданий: тест открытого типа; контрольная работа рутинного типа; контрольная работа творческого типа.

Тип задания	Сложность	Продолжительность диагностики
Тест закрытого типа	S1	3,25*S1
Тест открытого типа	S2	3,75*S2
Контрольная работа рутинного типа	S3	2, 5*S3
Контрольная работа творческого типа	S4	5,2*S4

Рис. 7. Продолжительность диагностики для заданий разного типа

Как следует из данных, числа 3,25; 3,75; 2,5; 5,2 являются коэффициентами масштабирования сложности для студента и остаются постоянными в рамках типа задания не зависимо от сложности S1, S2, S3, S4 самого задания.

Оценка продолжительности решения задания смешанного типа

На практике, при оценке качества владения компетенцией, часто встречаются задания смешанного типа, т.е., например, задание – тест сложности 10 (мин/раб) содержит 8 вопросов закрытого и 12 вопросов открытого типа. В этом же задании предусмотрено также контрольная работа: 2 задачи общей сложности 5 (мин/раб) рутинного типа и 1 задача сложности 7 (мин/раб) творческого типа.

Вопрос: сколько времени надо дать студенту для выполнения всего задания?

Рассмотрим пример расчета продолжительности тестирования:  Т(тест) =

(8/20) * 10 * 3,25 +(12/20) * 10 * 3,75 = 35,5

Аналогично, вычислим продолжительность контрольной работы: Т(раб) = 1 * 5 * 2,5 + 1 * 7 * 5,2 = 48,9;

Итого: продолжительность выполнения задания Т(задание) = 35,5 + 48,9 = 84,4.

Выводы

• 1.    Методику расчета продолжительности выполнения задания для студента можно использовать на практике на определенном интервале изменения S. При значениях S, примерно, меньше 4(мин/раб) и больше 40(мин/раб) устойчивость коэффициентов масштабирования теряется (проявляется нелинейность образовательного пространства).

• 2.    Для оценки продолжительности времени для реализации больших проектов, требуется дополнительное исследование.