Численная оценка точности при пространственной дискретизации уравнений теплопроводности

виями уравнений математической физики конечно-разностными методами приходится аппроксимировать производные, как во внутренних точках исследуемой области, так и на границах. При этом производные по отдельным переменным или производные во внутренних точках исследуемой области, а также производные в граничных точках могут иметь различный порядок аппроксимации.

Здесь на базе численного решения дана оценка точности пространственной аппроксимации, как во внутренних точках исследуемой области, так и в граничных точках области и слоёв.

ОСНОВНЫЕ УРАВНЕНИЯ

Все последующие исследования проведены относительно безразмерной температуры θ ^k в безразмерной пространственной координате ξ и безразмерном времени τ . Они введены с помощью соотношений

^ = (r - D₀)/L^M, т = t / t*,

O k = [T^k(r,t) - T^k₀(r)]/T*.           (1)

Здесь r, t – пространственная координата и время; Tk(r,t) – неизвестная температура, t* и T* – характерное время и характерная температура, Tk0(r) – начальное значение температуры; k – номер текущего слоя (k = 1,2,…, М), Lk0 и Lk – начало и конец текущего слоя.

Уравнения теплопроводности в слоистой среде относительно безразмерных параметров записываются в виде [7]

O\ = Fo^k (ц_п^к O ^k,^ +_h^k O ^k, ^ ) + m      (2)

где введены обозначения

Ц_п ^к = X ^k / X *; u ' = ( X ^k Z X *)^ + n ц_п ^к / ^ ;

_m k = v ^k + Q^kt*Z T* p ^k c _E ^k;

Fo^k = X * t*/ (L*)² p ^k c _E ^k.             (3)

Из приведенных обозначений можно видеть, что µ11k связан с коэффициентом теплопровод- ности λk; µ 1k – параметр, связанный с изменениями теплопроводности, а также системой координат (прямоугольная n= 0, цилиндрическая n=1, сферическая n=3); λ*– характерная теплопроводность, ρk – плотность и cek – удельная теплоёмкость материала k-го слоя, Qk – внутренние источники тепла в k –ом слое, Fok – параметр Фурье [7]. Производная по соответствующей переменной обозначена нижним символом после запятой.

Граничные условия приняты в виде

θ ¹, _ξ = Bi₀¹[ θ ¹ – ϕ ₀ ( τ )] при ξ = L¹₀/ L* (4.а) θ ^М, _ξ = – Bi_L^М[ θ ^М – ϕ _L ( τ )] при ξ = 1.      (4.б)

Здесь введены обозначения

ϕ ₀ ( τ ) = ( T¹ – T¹₀)/T*;

ϕ _L ( τ ) = ( T^М – T^M₀)/T*,           (5)

а T10, TM0 – заданные температуры окружающей среды.

При переходе от k – ого слоя к k +1 – ому слою условия идеального теплообмена [7] принимаются в виде (1 Ј k Ј М–1)

θ ^k, _ξ = ( µ ₁₁^k+1 / µ ₁₁^k) θ ^k+1, _ξ ;

θ ^k = θ ^k+1 при ξ = L^k /L*,          (6)

а условия неидеального теплообмена –

θ ^k, _ξ = – Bi_L^k ( θ ^k – θ ^k+1) при ξ = L^k /L*;    (7.а)

θ ^k+1, _ξ = Bi₀^k+1 ( θ ^k+1 – θ ^k) при ξ = L ^k+1₀ /L*. (7.б)

Всюду выше (см. (4) и (7)) введены обозначения: параметры Био Bi0 k+1 определяются из равенств

Bi_L^k = α ^k_L L* / λ ^k ;

Bi₀^k = α ^k₀ L* / λ ^k,                (8)

где α ^k_L и α ^k₀ – коэффициенты теплообмена.

ДИСКРЕТИЗАЦИЯ УРАВНЕНИЙ

Входящие в уравнения теплопроводности (2) производные от температуры по координате ξ представлены их разностным аналогом с точностью до малых второго порядка. При этом производные в любой внутренней узловой точке p (2 ≤ p ≤ N^k) представляются в виде

( θ ^k, ξ ) p = ( θ ^k p+1 – θ ^k p–1 )/ 2 Δ ^k ;

( θ ^k, _ξξ )_p = ( θ ^k_p+1 + θ ^k_p–1 – 2 θ ^k_p)/ ( Δ ^k)² .       (9)

Здесь Δ ^kиN^k – длина отрезка и число отрезков, на которые разделена длина L^k – L^k₀ участка k– ого слоя.

После подстановки значений производных (9) в уравнения теплопроводности (2) можно получить для всех внутренних точек (2 ≤ p ≤ N^k; k =1,2,…, М) следующие соотношения

( ∂θ ^k/ ∂τ ) _p = A^k_p θ ^k_p–1 + B^k_p θ ^k_p +C^k_p θ ^k_p+1 + ω ^k_p . (10) Здесь введены обозначения

A^k_p = (Fo^k) _p [( µ ₁₁^k)_p / Δ ^k – ( µ ₁^k) _p /2) ] / Δ;

B^k_p = –2(Fo^k) _p ( µ ₁₁^k) _p /( Δ ^k) ²;             (11)

C^k_p =(Fo^k) _p [( µ ₁₁^k)_p / Δ ^k + ( µ ₁^k) _p /2) ] / Δ ^k.

Если полученные уравнения теплопроводности (10) проинтегрировать на участке времени от τn до τn+1 , то оно может быть записано в виде

_(Pk _{p )}n+1 _{( θ} k _{p–1 )} n+1 _{+ (R}k _{p )} n+1 _{( θ} k _{p )} n+1 ₊ + (S^k_p ) ⁿ⁺¹ ( θ ^k_p+1) ⁿ⁺¹ = ( Ω ^k_p) ⁿ.

Для любого момента времени τ

(n = 0, 1, ….) введены обозначения (P^k_p) ⁿ⁺¹ = – z Δ_τ (A^k_p) ⁿ⁺¹; (R^k_p) ⁿ⁺¹= 1 – z Δ_τ (B^k_p) ⁿ⁺¹ ; (S^k_p) ⁿ⁺¹ = – z Δ_τ (C^k_p) ⁿ⁺¹ ;

( Ω ^k_p) ⁿ⁺¹ = z Δ_τ ( ω ^k_p ) ⁿ⁺¹ +(1– z Δ_τ ) (A^k_p +B^k_p θ ^k_p +C^k_p θ ^k_p+1 + ω ^k_p) ⁿ.

=n

(12) Δ τ

θ ^k p–1

+

Здесь Δ _t – шаг по времени, а z – параметр “неопределенности”, характеризующий используемую расчетную схему (“явная”, “неявная”).

ОЦЕНКА ТОЧНОСТИ АППРОКСИМАЦИИ

Таким образом получена двухмерная (по пространственным точкам р и этапам по времени n) разрешающая система нелинейных разностных уравнений (12) задачи нестационарной теплопроводности. При этом производные в любой внутренней узловой точке p ( 2 ≤ p ≤ N^k) представляются в виде (9) со вторым порядком аппроксимации по пространственной координате ξ . Замена уравнений (10) уравнениями (12) осуществлена с первым порядком аппроксимации по временной координате τ . Можно заметить, что порядок аппроксимации по временной координате является одним и тем же - первым, как в начальной точке (n = 1), так и во всех других точках (n>1). При этом по временной координате локальный порядок аппроксимации совпадает с глобальным порядком.

ВНУТРЕННИЕ ТОЧКИ

В конечно-разностной модели (12) производные по пространственной координате ξ дифференциальных уравнений (2) в любой внутренней узловой точке p (2 ≤ p ≤ N^k) представлены в конечном виде (9). Принятые выражения (9) являются приближенными и могут быть причиной несоответствия решения конечно-разностного уравнения (12) и исходного уравнения (2). Ниже проведены оценки погрешности аппроксимации соотношениями (9) производных, входящих в уравнения (2).

Соотношения (9) получены из представлений

-

[(…)^k, ξ ] p = [(…)^k p+1 - (…) ^k p - 1 ]/2 Δ ^k

- (1/3)[(…)^k, _ξξξ ]_p ( Δ ^k)² +R₁( Δ ^k)³ [(…)^k, ξξ ] p =[(…)^k p+1 - 2(…)^k p +(…)^k p - 1 ] /( Δ ^k)² - (1/12)[(…)^k, _ξξξξ ]_p( Δ ^k)²+ R₂( Δ ^k)⁴

-

В соотношениях (14) R₁( Δ ^k)³ и R₂( Δ ^k)⁴ являются остаточными слагаемыми в выражениях для первой и второй производной более высокого порядка малости.

Если в представлениях производной (14) вынести за скобки первое слагаемое, совпадающее с выражениями (9), то составляющие, отличающиеся (9) от (14), могут быть представлены

S kip = 2 A ^k ;(I3)|(^) ' , I p. ( A k )² - R/A k )³}/ / ,      p^... ) ^kp—1 ] ;              (15)

5 ^k 2p = ( A ^k )²{(1/12)[(.)^k Jp ( A ^k)²- R₂( A ^k)⁴}/

/ [(-)^k p+1 — ²(-) kp ⁺ (-)^k .J

Выражения δ ^k_1р и δ ^k_2рсчитаются малыми по сравнению с 1, что и позволяет использовать соотношения (9). Однако насколько они меньше единицы следует выяснить.

Ниже проведена оценка точности аппрокси-

следующих граничных условиях

А т при 0 < т < т ₁.

при ^ = r₀/ r_L и 0 , ^ = 0 при ^ = 1. (18) А т ₁ при т ₁ < т < т ₂

Ф ^{( т )} = {

мации непосредственными вычислениями величин δ ^k_1р и δ ^k_2р. При проведении указанных оценок предполагается, что главным членом в пред-

ставлениях (14), которые не учитывались в выражениях (9), являются слагаемые, содержащие третью производную. Третья производная находится из следующих выражений:

• -    во внутренних точках p (3 ≤ p ≤ N^k–1)

[('A ^p - KA +2 ²-^> . +1 ⁺²(^) p - 1 —

• - . - 2 ] / 2( A ^k)³ - R ( A ^k)²;          (16)

• -    в прилегающей к левой границе крайней

внутренней точке р = 2

[(_)_ч^ = HA +3(.) 3 + (...)- 3(_) 2 ]/

/ A ^{k 3}+ 0.5[(_)₄ A + Ri V ).

- в прилегающей к правой границе крайней внутренней точке p = Nk

[(•A A = [(^) p+1 - ³(^) p ⁺³(^) p - 1 - (. p - ₂]/ /( A ^k)³ + 0.5[(_)_ч A + R ( A )

Если использовать представления (16), то главное слагаемое параметра точности δ ^k_1р в выражении первой производной принимает вид

;V

= [(A

На внутреннем радиусе ξ = r₀/ r_L температура линейно растет до момента времени t₁, затем она поддерживается постоянной в течение промежутка времени τ ₁ ≤ τ ≤ τ ₂. На наружной поверхности цилиндра ξ = 1 (r = r_L) предполагается, что обмен с внешней средой запрещен, т.е. градиент температуры равен нулю.

Здесь же на рис. 1.б приведена зависимость отношения производных температуры третьего и первого порядков для внутренних точек многослойного цилиндра, вычисленные по формулам (17). Прежде всего, можно видеть, что максимальное значение этого отношения составляет 0,0099 (в правом верхнем углу рисунка 1 приведено его значение f_max). Обращает внимание, что наибольшие значения это отношение δ ₁ принимает вблизи граничных точек. Это означает, что условие “хорошей” аппроксимации δ ₁<< 1 может выполняться во внутренних точках исследуемой области и нарушаться в граничных. Поэтому важно обеспечить хорошую аппроксимацию, в том числе, в граничных точках.

В табл. 1 приведена полученная непосредственными вычислениями зависимость отношения производных δ ₁ от величины Δ ^k, которая характеризует густоту расположения узловых точек. Можно видеть, что с увеличением числа узловых точек N^k, что равносильно уменьшению шага по пространственной координате Δ ^k, отношение производных δ ₁ уменьшается (см. пятую строку). Этот результат свидетельствует о том, что точность аппроксимации (9) с ростом числа узловых точек повышается и решение, построенное в [7] на основе конечно-разностной модели, приближается к решению дифференциального уравнения (2).

Полученный численный результат на частном примере имеет общую закономерность. Эта закономерность может быть установлена на основе нижеследующих рассуждений. С целью выявления указанной закономерности выражения (17) для отношения производных третьего и первого порядка необходимо переписать в виде отношения производных первого порядка

⁵ 1 = [( ^{0 ,} , ) p +1. - ²( ^{0 ,} , ) p ⁺( ^{0 ,} , ) p-1.5 ] / ²( ^{0 ,} , ) p (¹⁹.а) для внутренних точек p (3 ≤ p ≤ N^k–1)

5 1 =[ - ( 0 , ^ ) 3, +2( 0 , _e )₂₅-( 0 , _e ) 1J / 2( 0 , ^ )₂      (19.6)

для прилегающей к левой границе крайней внутренней точке р = 2 и

⁵ 1 = [( ^{0 ,} , ) p+0. - ²( ^{0 ,} , ) p-0. ⁺( ^{0 ,} , ) p-1J / ²( ^{0 ,} , ) p (¹⁹.в) для прилегающей к правой границе крайней внутренней точке p = N^k.

+2(_)k

- 2(_)^k

p +2

p - ₂] / ,       p+1 - (^)^k p - 1 ]

для внутренних точек p (3 ≤ p ≤ N^k –1),

-

k

p +1

-

k

p - 1

-

(17.а)

5 ^k 1 =[ - (.)^k 4 +3(.)^k 3 + (.)^k 1 - 3(.)^k₂] /

/[(_)^k p+1 - (^)^k p - 1 ]               (17.6)

для прилегающей к левой границе крайней внут-

ренней точке р = 2 и

^{5 k} 1 =      >  .. ³-^> ' p +³(^)^k p - 1 -      >  p - ₂]/

/[(...y^-C..) ^k p - 1 ]                 (17.3)

для прилегающей к правой границе крайней внутренней точке p = Nk.

Справедливость утверждения, что приведенные выражения (17) для δ ^k₁ малы по сравнению с 1, не очевидна. В связи с этим была проведена

оценка точности аппроксимации (9) численным

сравнением отношения производных третьего и первого порядка по формулам (17) во всех внутренних точках p (2 ≤ p ≤ N^k) многослойного тела.

На рис. 1. представлено распределение температуры в трехслойном цилиндре в различные моменты времени, вычисленное на базе разработанной конечно-разностной модели [7] при

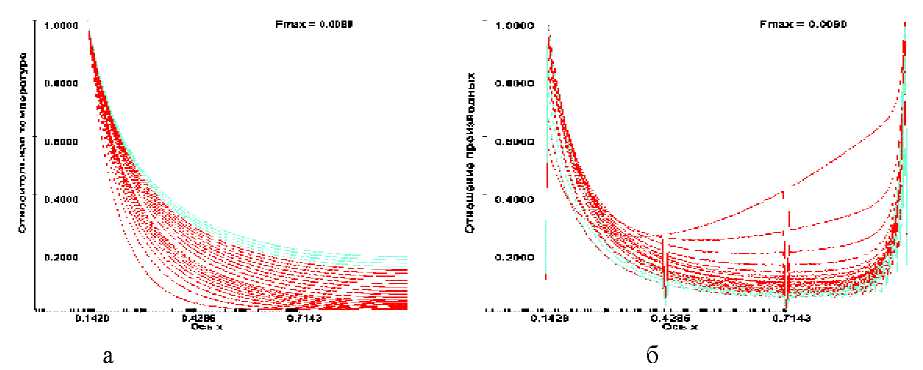
Рис. 1. Распределение температуры (а) и зависимость отношения производных температуры третьего и первого порядка (б) в трехслойном цилиндре на этапе повышения температуры на внутреннем радиусе и при выдержке температурного воздействия

Таблица 1. Зависимость отношения производных δ ₁от величины Δ ^k

Шаг по времени Ат-105	1.33
Число узловых точек в слое Nk	30	45	60	75	90
Шаг по пространственной координате (Ak) -103	9.52	6.35	4.76	3.81	3.17
Отношение Ат/(Ак)2	0.147	0.331	0.588	0.919	1.32
Максимальное отношение производных 8]-102	4.11	2.64	1.27	0.89	0.67
Максимальное отношение производных 82-102 с учетом граничных условий	75.97	25.64	14.89	9.69	6.79

При записи выражений (19) введены дополнительные узловые точки, а шаг по пространственной координате Δ ^k уменьшен вдвое. Например, узловая точка p +1.5 находится между узловыми точками р+1 и р+2.

Анализ соотношений (19) показывает, что с увеличением числа точек разбиения Nkвсе производные первого порядка приближаются к производной в исследуемой точке р. В числителе приведенных соотношений (19) стоят разности значений этих производных. Поэтому при Nk, стремящемся к бесконечности, указанные разности стремятся к нулю, в то время, как знаменатель принимает значение производной в узловой точке р. Этим объясняется эффект, приведенный в 5-ой строке таблицы 1 и установленный при решении частной задачи.

ГРАНИЧНЫЕ ТОЧКИ

В практике инженерных расчетов температурных задач конечно-разностным методом нередко используют второй порядок аппроксимации по пространственной координате ξ во внутренних точках (2 ≤ р ≤ М) и первый порядок аппроксимации производных в граничных точках. В этих случаях глобальный порядок аппроксимации первый, несмотря на то, что в большей части узловых точек локальный порядок аппроксимации равен двум.

При решении второй и третьей краевых задач нестационарной теплопроводности, а также при изучении температурных состояний слоистых сред в граничные условия (4), (6) и (7) входят производные первого порядка. Если для рассматриваемых многослойных тел использовать обсуждаемый широко распространенный подход, то первый порядок аппроксимации имел бы место во всех узловых точках, являющихся границей контакта соседних слоёв. Именно по этой причине на наружных поверхностях исследуемого тела, а также на поверхностях контакта соседних слоёв для аппроксимации производных используются соотношения (k =1,2,…,M)

( 9 ^k, ^ )₁ = (4 0 ^k 2 - 0 ^k₃ - 3 0 ^k 1 )/ 2 A ^k; (20.а) ( ⁰\ ) Nk +1 = — (^{4 0} k Nk — ⁰ k Nk-1 — ^{3 0} kNk +1 )/ ^{2 A} k . (²⁰-⁶)

Производные в этих точках с точностью до малых второго порядка могут быть представлены в виде (20), которые обеспечивают второй порядок аппроксимации. Этим достигается то, что глобальный порядок и локальные порядки аппроксимации становятся одинаковыми. В работе [3] предложен несколько другой способ вычисления производных, обеспечивающий второй порядок аппроксимации по пространственной координате.

Принятые выражения (20) являются приближенными и могут быть причиной несоответствия конечно-разностных представлений (20) исходным граничным условиям (4), (6) и (7). Оценки погрешности аппроксимации соотношениями (20) производных, входящих в граничные условия (4), (6) и (7), могут быть выполнены таким же путём, каким они были выполнены для внутренних точек.

Соотношения (20) получены из представлений |(^)^k,J₁ = [4(...)^k 2 - (^)^к 3 - 3(_)^к 1 ]/2 Л ^к +

■(I 3)|(^)^k_ | ( Л ) ' +

■(I l)|(^)^k_ ^^^ ] 1 ( Л ^к) 3 ;

(21.а)

|(^)^k, L, = — И...) / — 1 ₍^> ' — 2 — 3(^) k. | /2 Л ^к +(1/3) |(^)^k_ ^]р( Л ^к)²-

-(1/4) |(^)^к_     р Л ) ;

р = Nk +1

(21.б)

Для последующего анализа равенства (21) удобно записать в виде

'•’         (1+ 5 ^к > 4...) (_..) 3 _..) 2 Л (22.а)

|(^)^к- |_:, = - (1+ 5 ^к 2 ) |4(_)^к р - 1 -

• - (...)^к р - 2 —3(^)^к . ]/ 2 Л ^к; р = N +1, (22.б) в которых введены обозначения

5 2\м 1 4 (...), р ( Л ) (1 4 м . ,.м ^ х х (Лк)3}/ |i^!■    ,:^!'     3(^)кр];

р = Nk +1.                 (23)

Если параметры δk1 и δk2 малы по сравнению с 1, то аппроксимации (20) могут считаться приемлемыми.

Производные третьего порядка, входящие в равенства (23) вычисляются из равенств [(^)^k,,_K]₁ м..+ м..м 3 + )..) - (^)^к , ]/(Л^к)³ -м 2м...м V)

• _i. ..м_lV_!м..._!■м..._!._i..._!.■ + ...)■ +Мм...м )Лм (24)

Используя представления (24), главное слагаемое параметра точности δ ^k_р в выражении первой производной принимает вид

5 ^к , = |3(_)^к 3_!^> - 3 + (_)^к 4 - (_)^к 1 ] / |4(_)^к 2 -- (_)^к 3 - 3(_)^к , ]                (25а)

для первой точки слоя k (1, 2, …,М) и

^{5 к} 2      ³( ^’ р +³( ^’ р ' ^! р +     ■ р ]^/|⁴(^)^к р-1 -

- (^)^к р-2 - 3(^)^к р ]              (25.б)

для последней узловой точки р = Nk +1 k-ого слоя.

Были проведены численные исследования точности аппроксимации производных в граничных точках в совокупности с внутренними точками точно так, как это было выполнено для внутренних точек.

Анализ показал, что выполнение заданных условий, в которых в граничной точке производные равны нулю ( θ , _ξ = 0, см. соотношение (18)), может привести к большим погрешностям. По крайней мере, из приведенных равенств (25)

ясно, что в таких точках, если отношение разности производных к самой производной равно нулю, т.е. разность производных является малой более высокого порядка, чем сама производная при уменьшении D^k, то дискретизация в них законна. В противном случае такие точки должны быть исключены из рассмотрения. При численном решении задачи (18), благодаря условию θ , _ξ = 0 на границе ξ = 1, в этой точке параметр δ ^M₁ не вычислялся.

При достаточно гладком изменении теплофизических характеристик от слоя к слою на границе раздела слоёв не возникает дополнительных проблем, связанных с точностью аппроксимации в точках перехода от слоя к слою. Этот случай практически совпадает с тем, что приведено на рис. 1. Проблемы с точностью аппроксимации производных на граничных контактных поверхностях возникают при заметном отличии теплофизических характеристик в отдельных слоях. Это можно видеть из результатов расчетов для трехслойного тела, в котором коэффициент теплопроводности второго слоя на порядок меньше коэффициентов теплопроводности соседних (первого и третьего) слоёв. На рис. 2 приведены результаты вычислений, выполненные для такого трехслойного цилиндра. Следует заметить, что остальные параметры совпадают с теми, которые использовались при получении результатов, приведенных на рис. 1. Прежде всего, следует отметить, что максимальное значение параметра d^kдостигается как на наружной поверхности первого слоя, так и границах перехода от слоя к слою. При этом в последних точках слоя точность аппроксимации ниже ( δ ^k₂ >  δ ^k₁), чем в первых. Если для внутренних точек максимальное значение точности аппроксимации δ ^k составляло 0,0099 (см. рис. 1.б), то с учетом граничных точек параметр точности аппроксимации ( δ ^k₂) составляет всего 0.1107. Это означает, что точность аппроксимации в граничных точках в одиннадцать раз хуже, чем во внутренних точках. В табл. 1 в последней строчке приведены значения точности аппроксимации в граничных точках δ ^k₂ в зависимости от числа узловых точек. Тенденция повышения точности аппроксимации производных с увеличением числа узловых точек налицо. Однако точность аппроксимации с учетом граничных точек даже при принятой форме дискретизации производных (20) на порядок хуже, чем во внутренних точках.

То обстоятельство, что с увеличением числа узловых точек отношение производных третьего и первого порядка уменьшается и в граничных точках можно обосновать точно так же, как это было сделано для внутренних точек. В самом

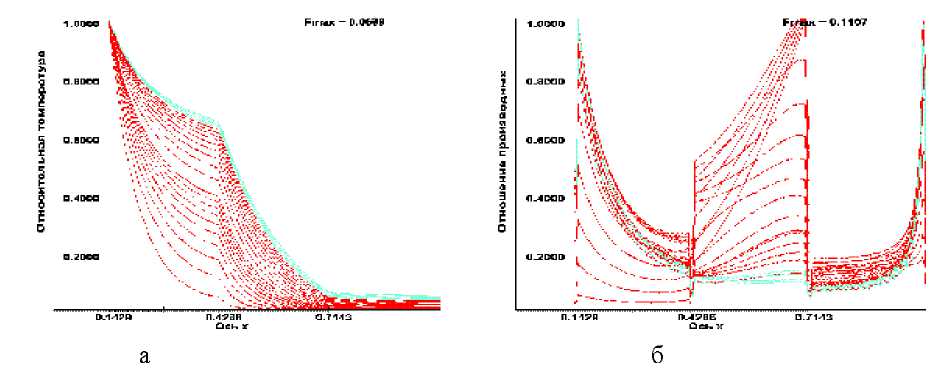
Рис. 2. Распределение температуры (а) и зависимость отношения производных температуры третьего и первого порядка (б) в трехслойном цилиндре с низким коэффициентом теплопроводности во втором слое на этапе повышения температуры на внутреннем радиусе и при выдержке температурного воздействия

деле, соотношения (25) можно записать в виде

• 5 k, = JC P ,^ - 2( 0 , ^ )₂₅+( 0 , ^ )_L5] / ( 0 , ^ ) 1      (26.а)

для первой точки слоя k (1, 2, …,М) и

• ⁵ k2 =[ —    ’ ., ⁺²(^U 5 — ( ^{0 ,},W   ’ . + (^26.б)

для последней точки слоя k (1, 2, …,М).

Из приведенных соотношений (26) можно видеть, что их числитель как разность производных первого порядка стремится к нулю при приближении узловых точек к граничной точке. В равенствах (26) предполагается, что производная в граничной точке отлична от нуля.

ВЫВОДЫ

Для обеспечения точности результатов численных расчетов, выполняемых с применением конечного разностного представления дифференциальных уравнений, порядок точности дискретизации в граничных точках не должен быть ниже порядка точности дискретизации во внутренних точках. Более того, порядок точности дискретизации в граничных точках, а не во внутренних, определяет точность конечно-разностной схемы решения нестационарных задач теплопроводности.