Численная оценка устойчивости разностных уравнений теплопроводности для многослойных сред

Здесь Δ ^k– длина отрезка, на которые разделена длина L^k – L^k₀ k–ого слоя ( Δ ^k =(L^k – L^k₀)/ N^k, N^k – число отрезков). Выбор отношения Δ _t / ( Δ ^k)² зависит как от характера изменения теплофизических свойств материала, так и параметра z. Ниже на основе разработанного алгоритма численного решения уравнений нестационарной теплопроводности [7] исследовано влияние различных параметров на выбор шага по времени Δ t, на обеспечение устойчивости решения конечноразностной модели нестационарной теплопроводности в слоистых (неоднородных) средах.

ОСНОВНЫЕ УРАВНЕНИЯ

Все последующие исследования проведены относительно безразмерной температуры qk в безразмерной пространственной координате x и безразмерном времени t. Они введены с помощью соотношений

• ξ = (r – L¹₀)/L^М, t = t / t*;

θ ^k = (T^k(r,t) – T^k₀(r))/T*            (1)

Здесь r, t – пространственная координата и время; Tk(r,t) – неизвестная температура, t* и T* – характерное время и характерная температура, Tk0(r) – начальное значение температуры; k – номер текущего слоя (k = 1,2,…, М), Lk0 и Lk–начало и конец текущего слоя.

Уравнения нестационарной теплопроводности [7] для слоистой среды относительно безразмерных параметров записываются в виде

θ ^k,_t = Fo^k ( µ ₁₁ ^k θ ^k, _ξξ +m₁^k θ ^k, _ξ ) + ω ^k ,       (2)

где введены обозначения

Ш1^к = X ^k / X *; m^k = ( X ^k I X *), § + n Щ1^к I ^ ;

_ю к ₌ v ^k ₊ Q ^k t*/ T* p ^k c _E ^k ;

Fo^k = X *t*I (L*)² p ^k c _e ^k.                   (3)

Из приведенных обозначений можно видеть, что µ11k связан с коэффициентом теплопроводности λk; µ1k – параметр, связанный с изменениями теплопроводности, а также системой координат (прямоугольная n= 0, цилиндрическая n=1, сферическая n=2); λ*– характерная теплопроводность, rk – плотность и cεk – удельная теплоёмкость материала k – ого слоя; Qk – внутренние источники тепла в k –ом слое; Fok – параметр Фурье [7]. Производная по соответствующей переменной обозначена нижним символом после запятой.

Граничные условия приняты в виде е1,^ = Bio1[e1 - ф 0 (т)], при ^ = L10/L*; (4.а) 0МЛ = - BiLM[еМ - ФL (т)], при ^ = 1 .   (4.б)

Здесь введены обозначения

ϕ ₀ (t) = ( T¹ – T¹₀)/T*;

ϕ _L (t) = ( T^М – T^M₀)/T*,                  (5)

а T10, TM0 – заданные температуры окружающей среды.

При переходе от k – ого слоя к k +1 – ому слою условия идеального теплообмена [7] принимаются в виде (1 ≤ k ≤ М–1)

e ^k, ₅ = (ци^к+1 / ц n^k) e ^k+1, _§ ;

e ^k = e ^k+1 при ^ = L^k /l* .             (6)

а условия неидеального теплообмена – в форме ek,^ = - BiL k(ek - ek+1), при ^ = Lk /l*; (7.а) ek% = Biok+1 (ek+1 -ek), при ^=Lk+1o/l* . (7.б)

Всюду выше введены параметры Био Bi0 k+1, которые определяются из равенств

BiLk = akL L* / Xk ; Biok = ako L* /Xk. (8)

Здесь α ^k_L и α ^k₀ – коэффициенты теплообмена на соответствующих поверхностях.

ДИСКРЕТИЗАЦИЯ УРАВНЕНИЙ

И МЕТОД РЕШЕНИЯ

Входящие в уравнения теплопроводности (2) производные от температуры по координате x представлены их разностным аналогом с точностью до малых второго порядка. При этом производные в любой внутренней узловой точке p ( 2 ≤ p ≤ N^k) представляются в виде

(ek,^)p = (ekp+1 - ekp-1)/ 2Ak;

( e ^k, ^^ ) p = ( e ^k p+1 + e ^k p-1 - 2 e ^k p )/ ( A ^k)² . (9)

После подстановки значений производных (9) в уравнения теплопроводности (2) можно получить для всех внутренних точек ( 2 ≤ p ≤ N^k; k =1,2,…, М) следующие соотношения

( de k / dr ) p =A^k p e kp-1 + B kp e kp +c k p e kp+1 + ® ^k p . (10) Здесь введены обозначения

A^k_p = (Fo^k) _p [( µ ₁₁^k)_p / Δ ^k – ( µ ₁^k) _p /2) ] / Δ ^k;

B^k_p = –2(Fo^k) _p (₁₁^k) _p /( Δ ^k) ² ;               (11)

C^k_p =(Fo^k) _p [( µ ₁₁^k)_p / Δ ^k + ( µ ₁^k) _p /2) ] / Δ ^k.

Если полученные уравнения теплопроводности (10) проинтегрировать на участке времени от tn до tn+1 , то оно может быть записано в виде

_(Pk _{p )}n+1 _{( θ} k _{p–1 )} n+1 _{+ (R}k _{p )} n+1 _{( θ} k _{p )} n+1 _{+ +(S}k _{p )} n+1_{( θ} k _{p+1 )} n+1 _{= ( Ω} k _{p )} n+1

Для любого момента времени

1, ….) введены обозначения (P^k ) ⁿ⁺¹ = – z Δ_τ (A^k ) ⁿ⁺¹, (R^kp) ⁿ⁺¹= 1 – z Δ_τ (B^pk ) ⁿ⁺¹, (S^k_p^p) ⁿ⁺¹ = – z Δ_τ (C^k_p)^pn+1, ( Ω ^k_p) ⁿ⁺¹ = z Δ_τ ( ω ^k_p ) ⁿ⁺¹ +(1– z

+B^k_p θ ^k_p +C^k_p θ ^k_p+1 + ω ^k_p) ⁿ.

Здесь Δ_τ – шаг по времени, а

.

τ =n Δτ (n = 0,

Δ τ ) (A^k p θ ^k p–1 + z – параметр

“неопределенности”, характеризующий исполь-

зуемую расчетную схему (“явная”, “неявная”).

Для каждого момента времени разностные уравнения (12) решаются методом прямой и обратной прогонки [5], обобщенной в [7] на многослойные конструкции.

На рис. 1. представлено распределение тем-

пературы в трехслойном цилиндре в различные моменты времени, вычисленное на базе разработанной конечно-разностной модели [7] при идеальном теплообмене между слоями и следующих

граничных условиях на наружных поверхностях А τ при 0 ≤ τ ≤ τ ₁.

при ξ = r₀/ r_L и θ , _ξ = 0 при ξ = 1. А τ ₁ при τ₁ ≤ τ ≤ ₂

На внутреннем радиусе ξ = r₀/ r_L температура линейно растет до момента времени τ ₁, затем она поддерживается постоянной в промежутке времени τ ₁ ≤ τ ≤ τ ₂. На наружной поверхности цилиндра ξ = 1 (r = r_L) предполагается, что обмен с внешней средой запрещен, т.е. градиент температуры равен нулю, что отчетливо можно видеть на рис. 1.

РАСЧЕТНАЯ СХЕМА. УСТОЙЧИВОСТЬ

Расчетная схема определяется параметром z (0 ≤ z ≤ 1), входящим в уравнения (12) (см. обо-

значения (13)).

Если в разрешающих уравнениях (12) положить параметр z равным нулю, то они преобразуются в форму явной конечно-разностной схемы

( θ ^k_p ) ⁿ⁺¹ = ( Ω ^k_p) ⁿ⁺¹ . (14)

Зависимости (14) позволяют непосредственно определить искомые значения температур ( θ ^k_p)ⁿ⁺¹ в момент времени τ = (n+1) Δ _t с помощью известного распределения температуры ( θ ^k_p)ⁿ в предыдущий момент времени τ = n Δ_τ . Действительно, правая часть уравнений (14) в соответствие

с (13) определяется из равенства

( Ω ^k p ) + C^k

p

n+1 θ ^k

p+1

( θ ^k_p) ⁿ + (A^k_p θ + ω ^k_p) ⁿ .

k p–1

+ B^k_p θ ^k_p +

Привлекательная простота явной расчетной

схемы упирается на ограничения при проведе-

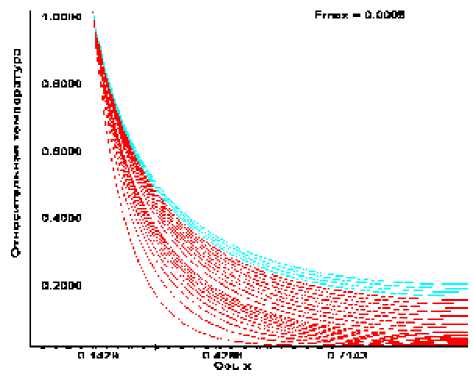
Рис. 1. Распределение температуры в трехслойном цилиндре на этапе повышения температуры на внутреннем радиусе (19 нижних линий) и при выдержке температурного воздействия (4 верхних линии)

нии непосредственных расчетов. Таким ограничением является устойчивость расчетной схемы. Анализ уравнений (15) показывает, что расчетная схема является устойчивой, если выполняется условие

1+ B^k_p= 1–2(Fo^k)_p( µ ₁₁^k) _p Δ_τ /( Δ ^k) ²і 0 или

2(Fo^k)_p( µ ₁₁^k)_p Δ_τ /( Δ ^k)² Ј 1 . (16)

Условие (16) согласуется с результатами оценки устойчивости решения, полученными в многочисленных исследованиях (см., например, [1] – [6] и др.).

Используя соотношение (16) и выбрав необходимую точность порядка аппроксимации, можно оценить требуемый шаг интегрирования по времени

Δ_τ ≤ ( Δ ^k)² / 2(Fo^k)_p( µ ₁₁^k)_p . (17)

Ниже в табл. 1 приведены расчетные значения критического интервала по времени ( Δ _t)_крит, полученные на основе соотношения (17) для обеспечения устойчивости решения в зависимости от размера сетки по пространственной координате Δ ^k. В табл. 1 параметр d₁ характеризует отношение отброшенных слагаемых при дискретном представлении (9) по сравнению с сохраненными.

Из анализа результатов, приведенных в табл. 1, можно видеть, например, что для того, чтобы точность аппроксимации (величина d1) не превышала 1% (см. 5-ый столбец, 4-ая строка – выделено жирным шрифтом), необходимо иметь безразмерную величину пространственной сетки Δk менее 5.71⋅10-3. В этих условиях шаг по времени Δτ не должен превосходить величины 0.458⋅10-5. Полученные оценки (Δτ)крит были проверены непосредственными вычислениями. Как видно из этого анализа шаг по времени Δτ должен быть достаточно малым для обеспечения одной и той же точности решения. Это создаёт определенные неудобства, особенно, при изучении длительно протекающих температурных процессов. Действительно, для проведения вычислений одной и той же задачи, требующей исследования в течение одного и того же календарного времени, минимальное число циклов по времени Nt в обсуждаемом случае составляет 6.55⋅105, вместо 1.0⋅105 по другой расчетной схеме. Таким образом, можно показать, что для обеспечения решения задачи с одной и той же точностью проведение вычислений по явной расчетной схеме требует значительных временных ресурсов.

Альтернативной расчетной схемой является неявная конечно-разностная схема, устойчивость которой обеспечивается при более слабых ограничениях (см., например, [3] – [5]). При использовании неявной расчетной схемы решают уравнения (12) при 0 < z ≤ 1, т. е. в этом случае на каждом временном шаге n Δ_τ приходится решать систему алгебраических уравнений (12). В настоящих исследованиях система алгебраических уравнений (12) решается методом прямой и обратной прогонки [5]. В подавляющем большинстве проведенных ниже исследований параметр z принят равным 0.5, что соответствует неявной расчетной схеме Крэнка–Николсона (см., например, [3]).

В работе [3] утверждается, что неявная расчетная схема является абсолютно устойчивой при 0.5 ≤ z ≤ 1 и условно устойчивой при 0 < z < 0.5. На рис. 2 приведены примеры расчетов, при выполнении которых не были учтены требования по обеспечению устойчивости решения.

Ниже путем проведения непосредственных вычислений для задачи с граничными условиями (4) установлены границы устойчивости при различных значениях параметра z (0 < z < 0.5;

Таблица 1.

Расчетные параметры	Значения расчетных параметров
Число узловых точек в слое Nk	15	20	30	50	60
Шаг по пространственной координате ( Δ k) ⋅ 103	19.5	14.3	9.52	5.71	4.76
Максимальное отношение производных δ 1 ⋅ 102	8.45	5.11	2.46	0.95	0.70
Критерий устойчивости ( Δτ )крит ⋅ 105	5.09	2.86	1.27	0.458	0.318
Необходимое число шагов по времени N τ⋅ 10 - 5	0.59	1.05	2.36	6.55	9.43

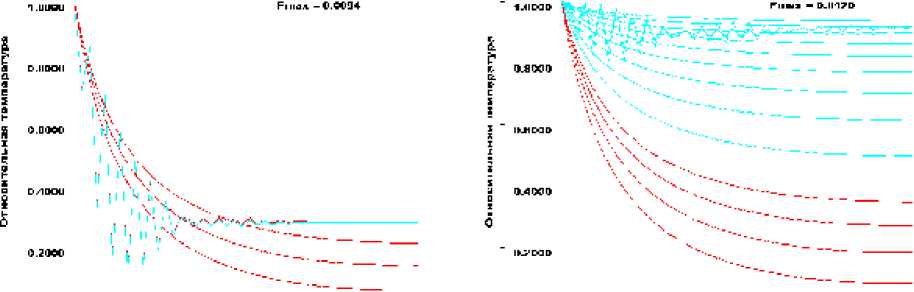
Рис. 2. Типичный характер численных решений при нарушении условия устойчивости

Таблица 2.

Расчетные параметры Число узловых точек в слое Nk 15 20 30 50 60 Шаг по пространственной координате (Δk) ⋅103 19.5 14.3 9.52 5.71 4.76 Максимальное отношение производных δ1⋅102 8.45 5.11 2.46 0.95 0.70 Γ⋅ (–1) ⋅102 6.79 9.7 4.4 1.07 1.01 Критерий устойчивости (Δτ)Крит ⋅105 6.0 3.47 1.47 0.56 0.387 Необходимое число шагов по времени Nτ⋅10-5 0.5 0.82 1.96 5.5 8.75 Γ⋅ (–1) 0.22 0.27 0.266 0.31 0.32 Критерий устойчивости (Δτ)Крит ⋅105 7.87 3.63 1.60 0.75 0.52 Необходимое число шагов по времени Nτ⋅10-5 0.46 0.79 1.81 4.9 7.77 Γ⋅ (–1) 0.57 0.69 0.70 0.64 0.74 Критерий устойчивости (Δτ)Крит ⋅105 11.3 6.67 3. 07 0.78 0.55 Необходимое число шагов по времени Nτ⋅10-5 0.33 0.57 1.63 4.6 7.52 Γ⋅ (–1) 1.55 1.70 1.85 1.81 2.00 Критерий устойчивости (Δτ)Крит ⋅105 21.5 12.8 6. 0 2.13 1.58 Необходимое число шагов по времени Nτ⋅10-5 0.25 0.43 1.31 3.12 6.01 см. табл. 2). В качестве критерия устойчивости используется параметр

Г = 1+ B^k_p= 1–2(Fo^k)_p( µ ₁₁^k) _p Δ_τ /( Δ ^k)², (18) из которого затем определяется предельная величина шага по времени D_t при известных значениях других параметров.

Анализ результатов вычислений, приведенных в табл. 2, показывает, что с требованиями по повышению точности аппроксимации (Nk –уве-личивается, Δk –уменьшается) снижается необходимая для обеспечения устойчивости решения длина шага по времени. При этом потребное для решения одной и той же задачи время увеличивается. Однако с ростом параметра z потребное время для решения одной и той же задачи снижается. Следует обратить внимание на то, что степень снижения числа шагов по времени с ростом параметра z снижается по мере увеличения требований к точности расчетов.

В [10] отмечается, что использованный в настоящей работе способ доказательства сходимости решения, полученного на основе конечноразностной модели (12), к точному решению дифференциального уравнения (2) путём проверки порядка аппроксимации и устойчивости носит общий характер.

ВЫВОДЫ

Впервые численно изучены проблемы, связанные с точностью аппроксимации дифференциальных уравнений конечно-разностной моделью и устойчивости решения.

Использованный здесь подход может найти широкое применение при выборе наиболее рациональных способов решения уравнений в частных производных методами дискретизации.