Численная оценка вероятностного распределения перетоков мощности

Значения перетоков активной мощности используются для соблюдения требований к устойчивости энергосистем при планировании и управлении электроэнергетическим режимом. Величины перетоков активной мощности зависят как от мощностей нагрузок в узлах сети, так и от параметров электрической сети. При создании математической модели исследуемой сети используется ряд допущений, например, мощность нагрузки задается конкретным числом на отдельных интервалах времени, хотя в действительности она не является постоянной величиной и может быть представлена некоторым интервалом, внутри которого находятся фактические значения [1]. Параметры сети также изменяются во времени под влиянием различных факторов, и их задание в виде постоянных величин вводит погрешность в рас- четы исследуемой сети [2, 3]. В частности, величина предельного перетока обратно пропорциональна сопротивлению рассматриваемой линии.

Оценка влияния колебаний нагрузок и изменения сопротивлений линий на изменение величины предельного перетока, а также оценка интервала его возможных значений может представлять интерес для дальнейшего использования величины предельного перетока в инженерных расчетах.

Вероятностный подход к расчету режимов

В настоящей статье предлагается применить на практике метод Монте-Карло (метод статических испытаний). Это численный метод, основанный на моделировании случайных величин и построении статистических оценок для искомых величин. Изменения нагрузки энергосистемы представляют собой суммирование изменений нагрузок отдельных электроприемников. Основное допущение состоит в том, что все одиночные электроприемники подключаются и отключаются независимо друг от друга. Как известно, независимое сложение достаточно большого числа случайных слагаемых приводит к нормальному распределению вероятности их суммы [4, 5].

Описание мощностей нагрузок нормальным распределением дает возможность решения задач достоверизации и обобщения результатов косвенной статистической оценки вероятностных характеристик колебаний небаланса мощности энергосистем и обменной мощности их объединения.

Реализация методики

Предлагаемый метод основан на проведении серий расчетов установившихся режимов при случайном изменении величин мощностей в узлах нагрузок сети, при случайном изменении величин сопротивлений линий или при сочетании этих изменений. С помощью ЭВМ моделируется вероятностный характер заданных величин. В этом случае случайная величина (мощность нагрузки каждого узла, сопротивление линии или их сочетание) задается законом распределения, а именно возможные значения случайной величины сопоставляются с вероятностями их появления. В рассматриваемой задаче предполагается, что случайная величина изменяется в 5%-ном диапазоне от своего исходного (номинального) значения и ее поведение описывается по закону нормального распределения. Реальные диапазоны изменения параметров схем замещения описаны в следующей литературе [6].

Расчеты установившихся режимов проводятся в программном комплексе RastrWin3 (далее ПК RastrWin3). Поскольку численный метод основывается на проведении большого количества расчетов, то для удобства использовались возможности специального пакетного обработчика схем, который отправляет исходные данные и принимает расчетные данные из ПК RastrWin3 и формирует таблицы с результатами расчётов в ПК MS Excel. Таким образом, обработчик обеспечивает взаимодействие с ПК RastrWin3 для автоматизации про- цесса перебора возможных значений нагрузок и параметров схем замещения в узлах исследуемой сети по заданному закону распределения.

В соответствии с методическими указаниями по устойчивости энергосистем [7] для определения предельного по статической устойчивости перетока осуществляется утяжеление режима, при этом рассматривается ряд траекторий утяжеления режима, которые характерны для данной энергосистемы и различаются перераспределением мощности между узлами. После чего значение предельной мощности определяется по траектории, которой соответствует наименьшая предельная мощность.

Для этого необходимо провести серию расчетов установившихся режимов, при которых в узлах сети задается предельная мощность по условиям статической устойчивости, а параметры случайных величин задаются в виде распределения. Часть режимов при этом не будут иметь решения вследствие нарушения статической устойчивости. По результатам расчетов остальных режимов станет возможным определить интервалы изменения предельного перетока, после чего появляется возможность определить необходимый коэффициент запаса устойчивости по активной мощности. Для этого нужно снижать исходную предельную мощность до такого значения, при котором в серии проводимых режимов не будет иметь место нарушение статической устойчивости. Отношение разности исходного значения предельной мощности P _пред и полученного значения мощности P _п ^у _р ^с _е ^п _д ^ех к исходному значению предельной мощности является необходимым коэффициентом запаса устойчивости по активной мощности:

успех пред пред kзап = p пред

Предложенная методика была реализована на двухузловых схемах «база – генератор» («Б–Г»), представленной на рис. 1, «база – нагрузка» («Б–Н»), представленной на рис. 2, на трехузловой схеме «база – нагрузка – генератор» («Б–Н–Г»), представленной на рис. 3, и на модели Редькино-

«+209.8-2977.5

Ген ^889.5 + 2188.4

89.95

-417.6 + 21955

«+38Э.5 +2188.4

94)1229 + 2576.8

1   121

2 ИС

Рис. 1. Результат расчета после утяжеления схемы «Б–Г»

Рис. 2. Результат расчета после утяжеления схемы «Б–Н»

База 115

лэп

ЛЭП

Harp

9.ЭБ + Л2.08

-ЮБ.4

9.96 + Л2.08

-ЮБ.4

ЛЭП

Г ан

Э.96 +J 1Z.08

-106.4

ЮЮ6 + ЛЛСЮ

-106.4

3   110

Рис. 3. Результат расчета после утяжеления схемы «Б–Н–Г»

Data

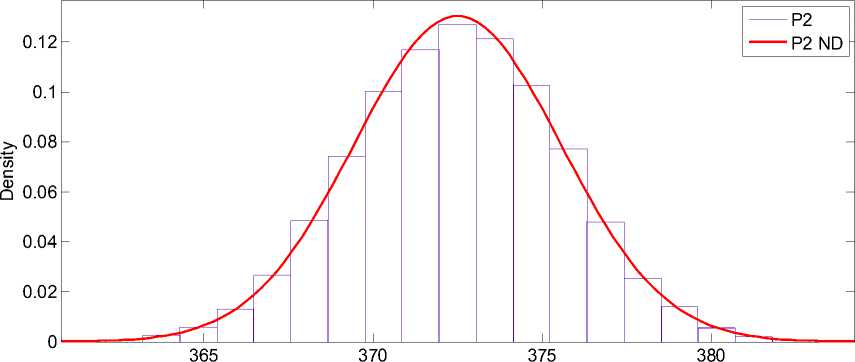
Рис. 4. Активная нагрузка в узле

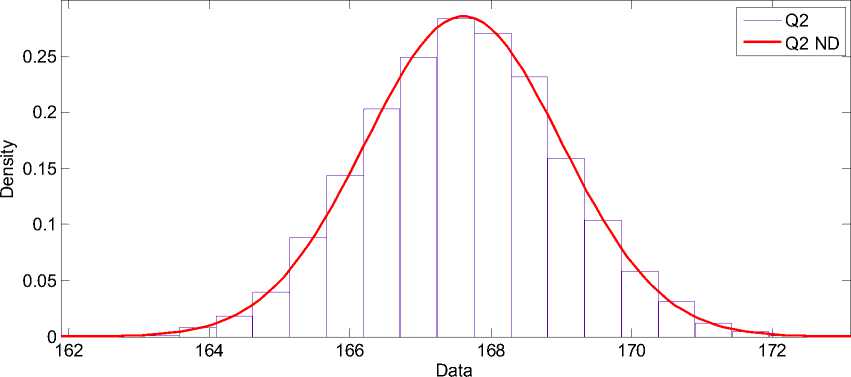
Рис. 5. Реактивная нагрузка в узле

Арланского района энергосистемы Республики Башкортостан. Расчётная модель составлена на основе данных СиПР [8].

Для каждой из предложенных схем проводится расчет 10 000 установившихся режимов при изменении исходных параметров сети в 5%-ном интервале значений. На рис. 4 и 5 приведены заданные распределения активной и реактивной мощностей нагрузок для узла 2 двухузловой схемы «база – нагрузка». Распределения сопротивлений для одной из двух линий двухузловой сети имеют аналогичный вид.

После проведения одной серии расчетов делается вывод о том, в каком процентном диапазоне изменялись перетоки мощности по ветвям исследуемой сети и определяются законы распределения величин этих перетоков.

Результаты

Были получены результаты перетоков активной и реактивной мощности линии для каждого успешно рассчитанного режима (без нарушения статической устойчивости). По полученным зна- чениям мощностей были построены их распределения и определены диапазоны изменения. Результаты перетоков для схемы «база – генератор» приведены на рис. 6 и 7.

Результаты реализации методики на двухузловой схеме «база – генератор» показали, что характер изменения предельного перетока активной мощности в начале линии при изменении сопротивления линий имеет нормальный закон распределения.

Характер изменения предельного перетока реактивной мощности в начале линии при изменении исходных значений активного и реактивного сопротивлений имеет полунормальный закон распределения. В двухузловой схеме «база – генератор» для поддержания напряжения в узле генерации изменяется реактивная мощность. Так как нерасчетные режимы были отброшены, изменение предельного перетока реактивной мощности выглядит как нормальное распределение, срезанное по одну сторону от значения с максимальной вероятностью.

Коэффициенты запаса активной мощности по статической устойчивости по параметрам начала и конца линии составили 7,90 и 2,02 % соответственно.

Результаты реализации методики на двухузловой схеме «база – нагрузка» показали, что характер изменения предельного перетока как активной, так и реактивной мощности в начале линии при изменении сопротивления линий, при изменении активной и реактивной мощности нагрузки или при их сочетании имеет нормальный закон распределения. Характер изменения напряжения в узле нагрузки 2 при изменении рассматриваемых исходных параметров также имеет нормальный закон распределения.

По аналогии с представленными ранее расчетами определяются коэффициенты запаса активной мощности по статической устойчивости по параметрам начала и конца линии для каждого значения интервала изменения исходных параметров сети. Результаты представлены в таблице и на рис. 8.

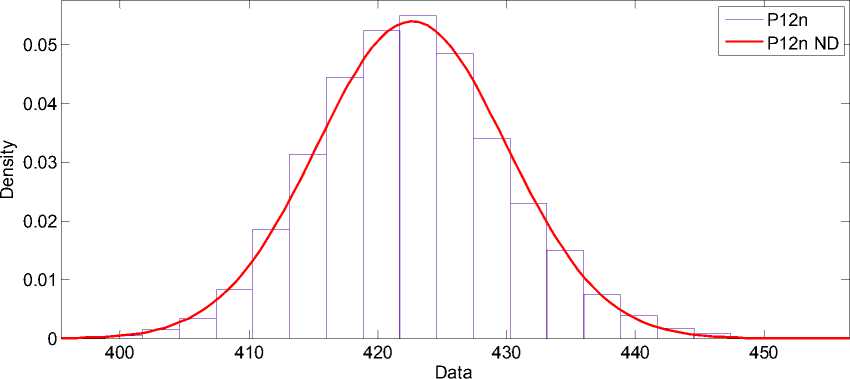
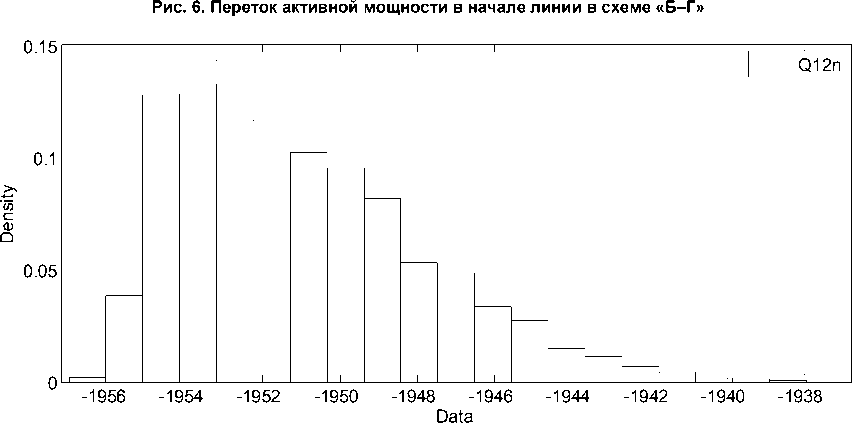
Рис. 7. Переток реактивной мощности в начале линии в схеме «Б–Г»

Как видно из рис. 8, коэффициенты запаса активной мощности по статической устойчивости по параметрам начала и конца линии увеличиваются с увеличением интервала изменения исходных параметров сети по линейной зависимости.

Результаты реализации методики на трехузловой схеме «база – нагрузка – генератор» показали, что характер изменения предельного перетока активной и реактивной мощности по линиям и напряжения в узле нагрузки 2 при изменении параметров исходного режима имеет закон распределения, отличный от нормального. Фактически эти параметры имели бы нормальный закон распределения при расчете нормальных режимов. Но в силу того, что часть нерасчетных режимов была отброшена, законы распределения приняли иной вид. Были получены качественно аналогичные двухузловой схеме «Б–Н» результаты зависимости значений коэффициента запаса от величины изменения исходных параметров.

Результаты реализации методики на примере модели Редькино-Арланского района энергосистемы Республики Башкортостан показали, что характер изменения предельных перетоков активной

Зависимость значений коэффициента запаса от величины интервала изменения исходных параметров сети

Разброс исходных параметров, %	СКО, МВт	P п у р с е п д ех нагрузки, МВт	P успех в начале линии, МВт пред	k знап , %	k зкап , %
5	2,440	360,30	500,32	12,69	3,28
10	4,897	352,91	477,47	16,68	5,26
15	7,337	343,15	452,18	21,09	7,89
20	9,922	332,81	428,84	25,16	10,65
25	12,261	323,46	409,67	28,51	13,16

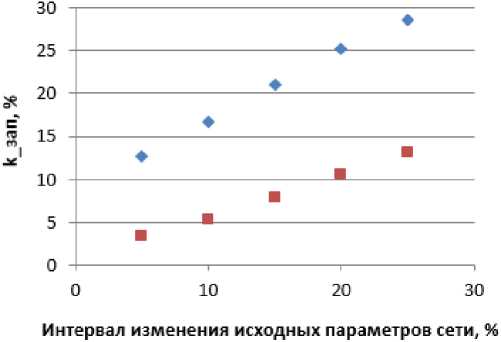
♦ к зап н

■ к за п к

Рис. 8. Зависимость значений коэффициентов запаса от величины интервала изменения исходных параметров сети

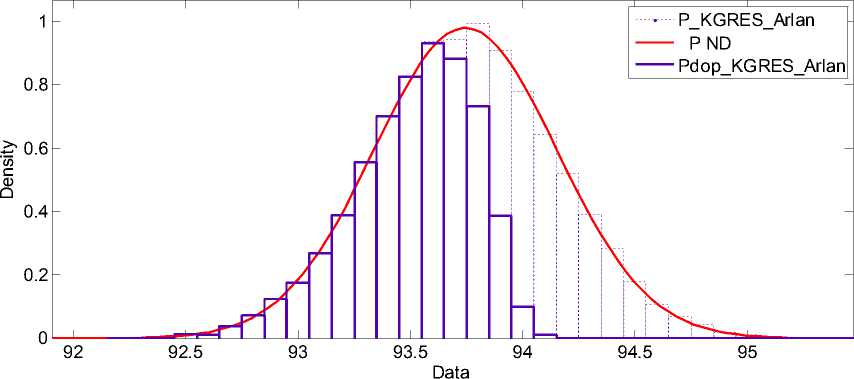
Рис. 9. Предельный по токовой загрузке переток активной мощности по ВЛ 110 кВ Кармановская ГРЭС – Арлан

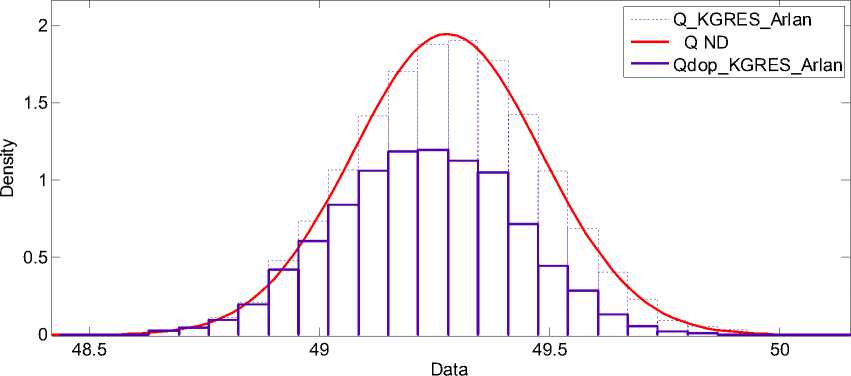
Рис. 10. Предельный по токовой загрузке переток реактивной мощности по ВЛ 110 кВ Кармановская ГРЭС – Арлан

и реактивной мощностей по линиям при изменении исходных параметров энергосистемы имеет нормальный закон распределения. Были получены результаты перетоков активной и реактивной мощности линий 110 кВ, отходящих от Карманов-ской ГРЭС, и результаты величин напряжений в узлах сети по концам этих линий. При построении законов распределения перетоков мощности и напряжений на рисунках отдельно выделены результаты, оставшиеся после отбрасывания этих режимов. На рис. 9 и 10 представлены результаты перетоков для ВЛ 110 кВ Кармановская ГРЭС – Арлан.

Заключение

В работе была проанализирована чувствительность перетоков мощности к изменению величин мощностей в узлах нагрузки и параметров сопротивлений сети. Методика исследования заключалась в проведении серий расчетов установившихся режимов при изменении мощностей в узлах нагрузки и параметров сопротивлений сети по заданному закону распределения. По результатам каждой серии расчетов были определены величины перетоков мощности по линиям рассматриваемой энергосистемы и напряжения в нагрузочных узлах сети, диапазоны их возможных значений и законы распределения с выводами о характере изменения параметров сети в указанных условиях. Кроме того, были оценены коэффициенты запаса в предельных режимах.

Были проведены серии расчетов режимов для различных схем сети:

• •    двухузловая схема «база – генератор»;

• •    двухузловая схема «база – нагрузка»;

• •    трехузловая схема «база – нагрузка – генератор»;

• •    модель Редькино-Арланского района энергосистемы Республики Башкортостан.

Результаты расчётов показали, что на пере- численных схемах при изменении исходных параметров сети в заданном (5 и 10 %) диапазоне значений по нормальному закону распределения расчетные перетоки активной мощности по ветвям сети колеблются в диапазоне значений 0,72–22,7 %, а напряжения в узлах сети колеблются в диапазоне значений 0,002–24,19 %. Диапазон разброса зависит от схемы сети, её параметров и вида установившегося режима (нормальный, предельный). Стоит отметить, что в нормальных режимах распределение указанных расчетных параметров внутри полученных интервалов их значений может быть представлено нормальным законом распределения.

Распределения расчетных параметров, отличные от нормального закона, были получены в предельных режимах при расчете следующих схем:

• •    «база – генератор» (полунормальный закон распределения изменения предельного перетока реактивной мощности);

• •    «база – нагрузка – генератор» (закон распределения изменения предельного перетока активной и реактивной мощности по линиям, а также напряжения в узле нагрузки);

• •    модель Редькино-Арланского района энергосистемы Республики Башкортостан (полунор-мальный закон распределения при отбрасывании режимов с превышением длительно допустимой токовой загрузки по линии 110 кВ Кармановская ГРЭС – Арлан).

Законы распределения указанных параметров в перечисленных расчетных ситуациях отличаются от нормального в силу того, что часть нерасчетных режимов была отброшена. В том случае, когда в серии каждый из 10 000 установившихся режимов является расчетным, распределение указанных расчетных параметров внутри полученных интервалов их значений представляется нормальным законом распределения.

Результаты численного моделирования на примере модели Редькино-Арланского района энергосистемы Республики Башкортостан показали, что характер изменения перетоков активной и реактивной мощностей по линиям, а также напряжения в узлах сети имеют нормальный закон распределения при расчете нормальных установившихся режимов.

Был выявлен предельный режим работы сети, который характеризуется максимально допустимой токовой загрузкой линии 110 кВ Карманов-ская ГРЭС – Арлан. В серии из 10 000 расчетных ситуаций все установившиеся предельные режимы (по токовой загрузке линии 110 кВ Кармановская ГРЭС – Арлан) являются расчетными. Распределения указанных расчетных параметров внутри полученных интервалов их значений представляются нормальным законом распределения. Но в 3783 из 10 000 режимов наблюдалось превышение максимально допустимой токовой загрузки линии. После отбрасывания этих режимов распределение указанных расчетных параметров внутри полученных интервалов их значений представляется законом распределения, отличным от нормального.

При 5%-ном отклонении исходных значений активного и реактивного сопротивления линий и значений активной и реактивной мощностей в узлах нагрузки в предельном режиме 99,7 % расчетных значений перетока активной мощности по линии 110 кВ Кармановская ГРЭС – Арлан находится в интервале 1,30 % относительно его математического ожидания. При этом полный разброс величины перетока активной мощности составил 3,41 %. Без учета режимов с превышением длительно допустимой токовой загрузки по линии 110 кВ Кармановская ГРЭС – Арлан в указанных выше исходных условиях полный разброс величины предельного перетока активной мощности по этой линии составил 2,14 %.

Аналогично 99,7 % расчетных значений перетока реактивной мощности по линии 110 кВ Кар-мановская ГРЭС – Арлан находится в интервале 1,25 % относительно его математического ожидания. При этом полный разброс величины перетока реактивной мощности составил 3,43 %. Без учета режимов с превышением длительно допустимой токовой загрузки по линии 110 кВ Кармановская ГРЭС – Арлан при указанных выше исходных условиях полный разброс величины предельного перетока реактивной мощности по этой линии составил 3,03 %.

При 5%-ном отклонении исходных значений активного и реактивного сопротивления линий и значений активной и реактивной мощностей в узлах нагрузки 99,7% расчетных значений напряжения в рассмотренных узлах сети находятся в интервале около 0,14 %.

Коэффициенты запаса активной мощности по параметрам начала и конца линии составили 1,36 и 1,31 % соответственно. Следовательно, существующих коэффициентов запаса устойчивости по активной мощности (20 % в нормальном режиме и 8 % в послеаварийном режиме) достаточно для поддержания параметров режима в допустимых пределах.