Численная реализация метода геометрического погружения на основе вариационного принципа Кастильяно

Для решения задач теории упругости тел сложной, в том числе и пространственной, конфигурации предложены эффективные итерационные методы: метод геометрического погружения [1], метод фиктивных областей [2, 3]. Метод геометрического погружения представляет собой процедуру сведения краевой задачи, сформулированной на области произвольной конфигурации, к итерационной последовательности задач на некоторой канонической области. Существует обобщение идеи метода геометрического погружения на класс задач линейной и нелинейной вязкоупругости [4-6], упругопластичности [7]. В перечисленных работах итерационно-вариационная процедура метода геометрического погружения строится в рамках вариационного принципа минимума общей потенциальной энергии. Метод геометрического погружения используется в совокупности с каким-либо численным методом. Использование метода конечных элементов в основной процедуре метода геометрического погружения позволяет получать конечномерные аналогии краевых задач со многими полезными качествами, зачастую не присущими обычным формулировкам метода конечных элементов. Реализация метода конечных элементов в рамках напряжений осуществляется в единичных случаях для тел канонической формы. Основная причина этого состоит в трудностях аппроксимации напряжений в конечном элементе. Решение задач в напряжениях обладает рядом преимуществ: автоматически исчезают проблемы, возникающие при вычислении напряжений в вариантах метода конечных элементов, основанных на постановке задачи в перемещениях; полученное решение представляет собой верхнюю грань оценки точного решения, а также отсутствуют проблемы для тел, изготовленных из несжимаемых и слабосжимаемых материалов. Представляет интерес формулировка и реализация метода геометрического погружения в рамках вариационного принципа минимума дополнительной энергии, в том числе конечно-элементная реализация.

Запишем функционал дополнительной энергии деформируемого тела в общем виде:

П_с = jd-8 dV -J t ■ UdS u ,                  (1)

V             Su где V - объем, занимаемый исходной областью, Su - часть поверхности на которой заданы кинематические граничные условия, t - вектор усилий на Su , U - вектор заданных перемещений на Su , d - тензор напряжений, 8 - тензор деформаций.

Функционал П_с определен на множестве функций ст _у (компоненты тензора напряжений), удовлетворяющих в области V уравнениям равновесия и статическим граничным условиям на границе S _d .

Следуя идее метода геометрического погружения [1], выполним тождественное преобразование выражения (1):

V

V д

S u

V д

где V - объем области, дополняющей исходную область V до канонической V ₀ ( V ₀ = V и V ).

Функционал (2) можно привести к виду

П с

V 0

2 Va

j t • U J dS u .

S u

Из функционала (3) следует вариационное уравнение

^V 0               ² V a                ^S u

Будем решать уравнение (4) итерационным методом в виде

Vo                       2 V a                     Su где k - номер итерации метода геометрического погружения; a0 = 0.

Таким образом, метод геометрического погружения сводится к итерационной процедуре, где на каждой итерации решается задача теории упругости в напряжениях в области V0. Область V0 является канонической, для которой решение задачи теории упругости получить значительно проще.

В данной работе рассмотрены примеры реализации метода геометрического погружения на основе вариационного принципа Кас-тильяно.

В качестве первого шага рассмотрим решение плоской задачи теории упругости, известное как аналитическое решение. На данном этапе решалась осессимметричная задача об определении напряжений в кольцевой области, внутренний радиус которой r 1 = 10² м, внешний r ₂ = 2 • I0 2 м, жестко закрепленной по внешнему радиусу и нагруженной по внутреннему радиусу постоянным давлением P_r = 100 кг/см², касательные напряжения на внутренней поверхности отсутствуют (рис. 1). Решение ведется в полярной системе координат с использованием функций напряжений. Область разбивается кольцевыми элементами, связанными друг с другом только в узловых окружностях.

При построении конечно-элементных соотношений для задачи, сформулированной на основе принципа Кастильяно, требуется обеспечить равновесное поле напряжений внутри элемента и на межэлементных границах. Использование функции напряжений обеспечивает ус- ловие равновесия внутри элемента. Равновесие на границах элементов для данной задачи можно обеспечить, если будут совпадать значения функции напряжений ф и ее производной — в узловых окружностях ar   - соседних элементов. Для этого выберем их в качестве узловых неиз вестных элемента:

дф

1ф г , ~, ф j a r

a r

T

где i , j - номера соседних узловых окружностей,

(фе}

- вектор узло

вых неизвестных элемента.

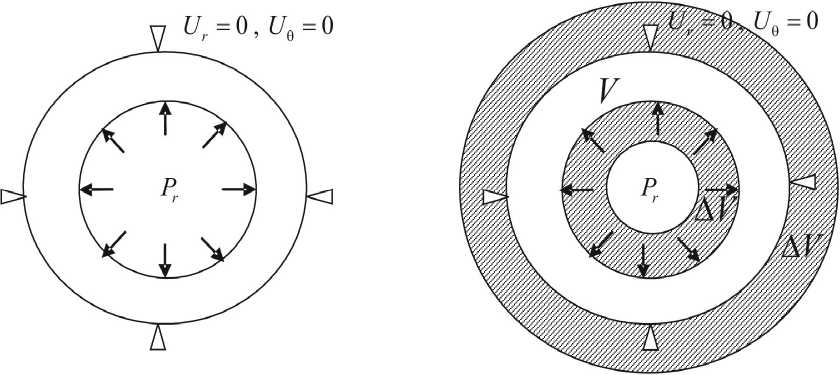
Рис. 1. Схема кольцевой области

Рис. 2. Схема погружения

Изменение функции напряжений в элементе представлено в виде полинома:

Функцию напряжений можно записать в другом виде:

ф - Noiфi + Nи-ф + Nо j ф, + Nij ^j, д r               д r

где N ₀ i , N 1i , N ₀ j , N₁ j - функции формы конечного элемента.

Неизвестные коэффициенты полинома (7) а1? а2, а3, а4 нахо дим из условий:

d Ngn ( rm )

d f        a g О nm , f , ^{g —} 0, ¹ , n , m ^— i , J .

Результаты, полученные методом конечных элементов, сравни ваются с точным аналитическим решением, в результате чего получены зависимости погрешностей радиального напряжения, окружного напряжения и перемещений от числа узловых неизвестных M .

До rr = mах |о ur-o rri |До a| |,

До66 = max |оQ6/-° е^|/|° a| I,

Д Ur = max |ur-ua\l\ua\|,(12)

где ||о ^a || = max ( о " i , о ^ ₆ J, о Or , о ^ ₆ i - значения напряжений точного

|| u^a | | = max ( U ra ) ,

аналитического решения в i -й узловой окружности, ur - значение перемещения точного аналитического решения в i -й узловой окружности, о Ur, о U6 i - значения напряжений численного решения в i -й узловой окружности, uu - значение перемещения численного решения в i -ой узловой окружности, i - целое число, пробегает значения от 1 до M .

Из рис. 3-5 видно, что с увеличением количества элементов погрешность метода конечных элементов уменьшается. По результатам метода конечных элементов для данной задачи можно говорить о сходимости метода к точному решению.

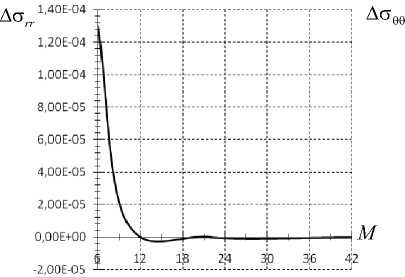
Рис. 3. Зависимость относительной погрешности о rr от числа узловых неизвестных

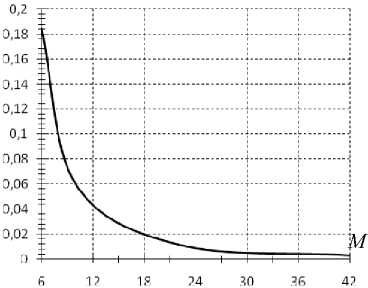
Рис. 4. Зависимость относительной погрешности о66 от числа узловых неизвестных

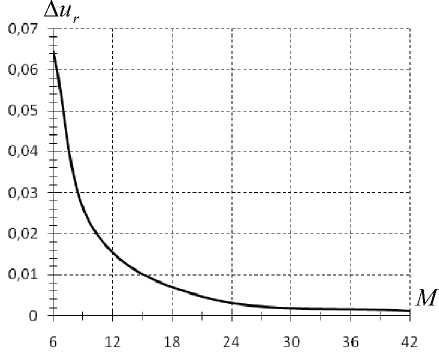
Рис. 5. Зависимость относительной погрешности и от числа узловых неизвестных

Рассмотрим далее в качестве иллюстрации применение процедуры метода геометрического погружения (3) для решения данной задачи. Для этого осуществим погружение конструкции в некоторую каноническую область, в качестве которой выберем кольцо меньшего внутреннего r/ = 0,5 -10 2 м и большего наружного радиусов r2' = 2,5 -10 2 м (рис. 2). В итерационной процедуре метода геометриче ского погружения для решения задачи теории упругости на канонической области используется ранее описанная схема метода конечных элементов. Для канонической области V0 сетка содержит 40 элемен тов, из них 20 приходится на область V , 20 - на область V . Остановка итерационной процедуры происходила при выполнении условия max n

Ф n

Ф

к - 1

n

Ф

к - 1

n

дфк дф к-1

дг____dr я к-1

дФ n

где n = 1, M. Полученные результаты сравнивались с аналитическим решением. При выбранном 5 = 10-7 для достижения требуемой точности потребовалось 10 итераций.

Относительная погрешность напряжений и перемещений метода геометрического погружения отличается от погрешности метода ко- нечных элементов максимально на 10-4. Графики зависимостей аналогичны графикам, представленным на рис. 3-5. Таким образом, для данной задачи метод геометрического погружения сходится и дает результаты, близкие к точному решению.

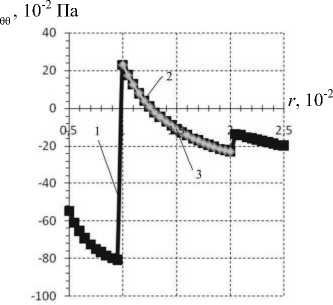
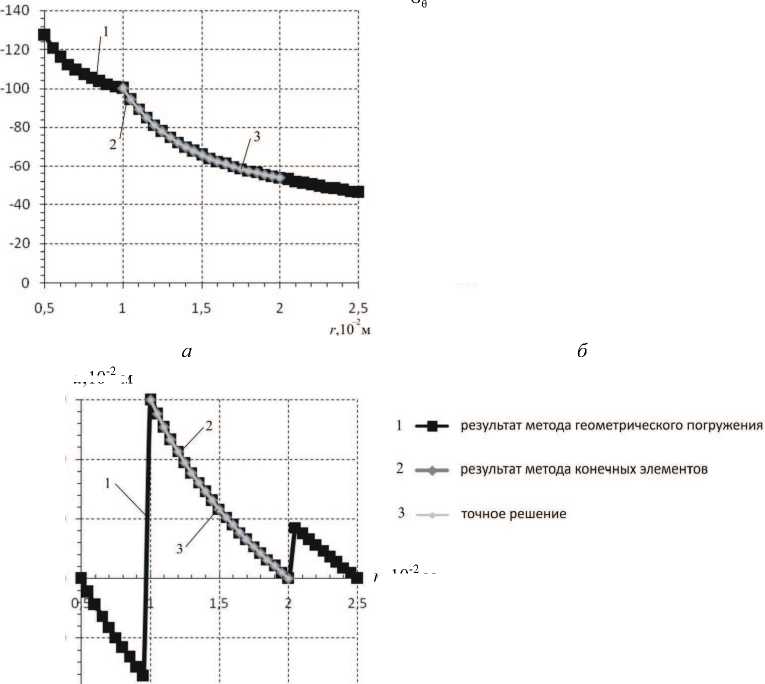
Графики, представленные на рис. 6, демонстрируют распределение найденных напряжений и перемещений от радиуса, а также выполнение естественных граничных условий в перемещениях. Результаты метода геометрического погружения показаны с учетом добавочной области V .

м

_а , 10^-2 Па rr

и ,10 м

З.ООЕ-Ю

2.00Е-10

1.00Е-10

r , 10 м

0,00Е+00

-1.00Е-10

-2,00Е-10 J

в

Рис. 6. Результаты решения первой задачи: а - радиальные напряжения; б - окружные напряжения; в - перемещения

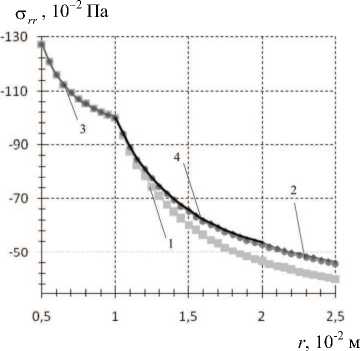
Рис. 7 демонстрирует сходимость итерационной процедуры метода геометрического погружения: результаты первой итерации наиболее отличаются от точного решения задачи, уже на третьей итерации метод близок к точному решению: относительная погрешность радиального напряжения До rr = 0,2614 - 10^-4, окружного напряжения

До ₆₆ = 0,9470 - 10^-4, перемещений Дu r = 0,4658 - 10^-4.

u ,10

4.00Е-10

-2,00Е-10

ст , 10 " ² Па ^о66 ’

3,00Е-10

2,00Е-10

1,ООЕ-1О

-1.00Е-24

-1,00Е-10

10-2 м

б итерация метода геометрического погружения итерация метода геометрического погружения итерация метода геометрического погружения r, 10 м

в решение

Рис. 7. Результаты решения первой задачи для первых трех итераций метода геометрического погружения: а - радиальные напряжения;

б - окружные напряжения; в - перемещения

В качестве более сложного иллюстративного примера осуществим реализацию алгоритма метода геометрического погружения для задачи, не имеющей аналитического решения, с усложненной геомет- рической конфигурацией. Решалась задача об определении напряжений в круговой области, внешний радиус которой r = 2 ■ 10 2 м, с внутренним эллиптическим вырезом, малая полуось которого a = 10 2 м, большая - b = 1,5■Ю 2м. На внутренней эллиптической поверхности заданы нормальные к границе области перемещения Un = 0,01 ■ 10-2 м, на внешней поверхности - статические граничные условия стr = — 1 кг/см2 и тr6 = 0 кг/см2 (рис. 8). Задача плоская, решение ведется в рамках линейной теории упругости в полярной системе координат, с использованием метода конечных элементов в напряжениях. Погружение осуществлялось в кольцо с внутренним радиусом r1 = 10—2 м и внешним радиусом r2 = 2,5 П0—2 м (рис. 9). Каноническая область разбивается кольцевыми элементами, связанными друг с другом только в узловых окружностях.

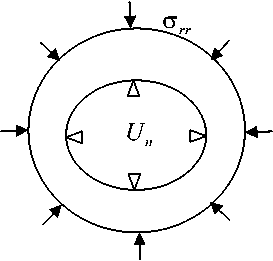
Рис. 8. Схема круговой области с эллиптическим вырезом

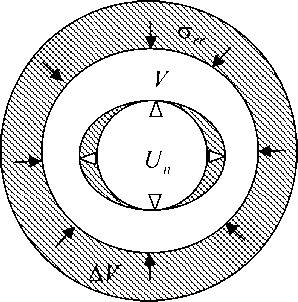
Рис. 9. Схема погружения

Каноническая область является телом вращения, поэтому функцию напряжений можно разложить в ряд по окружной координате:

да

ф( r, 0)=Е(ф n (r) n=0

■ cos ( n 0 ) + ф _n ( r ) ■ sin( n 0 ) ) .

Непрерывное поле напряжений внутри элемента и на межэлементных границах обеспечивалось путем выражения неизвестных коэффициентов линейной комбинации, удовлетворяющей бигармониче- скому уравнению, через напряжения в узловых окружностях. Функция напряжений аппроксимировалась следующими зависимостями:

ф₀ ( r ) = A <°> r ² + A 20) r ,

Ф 1 ( r ) = A 1 ⁽¹⁾ r ³ + A 21) r ² + A ₃ ⁽¹⁾ r -1 + A 41) r ^{- 2}, ф n ( r ) = A (n ) r ³ + A 2n ) r ² + A ₃ ^{( n} ) r + A 4 ⁿ ) , n >  1 .

Выражения для ф _n ( r ) при n > 1 аналогичны ф _n ( r ) , при n = 0 ф _n ( r ) = 0. Напряжения ищутся в виде ”

стr (r,0) = ^1 ^") (r) • cos (n0) + ^") (r) • sin(n0)), n=0

™ /                            x

« CTo(r,0) = ^la0n) (r)• cos(n0) + a0n) (r)• sin(n0)),(15)

n = 0 ^X

Tr0 (r. 0) = ^Ko) (r)^ cos (n0) + Tr0) (r)• Sin(n0) ) , n=0 V7

где G^k" ⁾⁽ r ), a 0 ^{n )(} r ), ^ r o) ⁽ r ) - коэффициенты при соответствующих гармониках:

при n =0

'е < »> = 2 A ,¹⁰) + A 20) r ".

^S” = 2 A ,¹⁰¹ ,                              (16)

т(0) - 0 ^T r 0 = 0, при n =1

V0 = 2 A ⁽¹⁾ r + A 2 ¹ ) - 2 A ₃ ⁽¹⁾ r - 3 - 3 A 4 ¹ ) r ■ ,

< ст О ¹ ) = 6 A 1 ⁽¹⁾ r + 2 A 2 ¹ ) + 2 A ₃ ⁽¹⁾ r ~³ + 6 A 41) r "⁴ ,               (17)

t® = A 1 ⁽¹⁾ r + A 2 ¹ ) + A ₃ ⁽¹⁾ r ^{- 3} + 3 A 4 ¹ ) r ^{- 4} , при n >1

'^ r ⁰⁾ = 2 A 1 ⁽¹⁾ r + A 2 ¹ ) - 2 A ₃ ⁽¹⁾ r ^{- 3} - 3 A 41) r ^{- 4} ,

« ст О ⁰⁾ = 6 A 1 ⁽¹⁾ r + 2 A 2 ¹ ) + 2 A ₃ ⁽¹⁾ r ^{- 3} + 6 A 41) r ^{- 4} ,               (18)

t r o = A 1 ⁽¹⁾ r + A 2 ¹ ) + A ₃ ⁽¹⁾ r ^³ + 3 A 4 ¹ ) r ^{- 4} ,

Выражения для or”)(r), c6n)(r), Tr^r) при n > 1 аналогичны c^) (r) , c^n) (r) , Tn (r), при n — 0 orn) (r) — 0, cn) (r) - 0, Tr6) (r) — 0.

Коэффициенты A ⁽⁰^ — A 4 ⁿ ) выражаются через значения узловых

(0)        ⁽⁰⁾        (1)        ⁽¹⁾        (1)        ⁽¹⁾        ( n)       ( n )       ( n)      ( n )

^{напряжениИ c} ri , ^c rj ,   ^c ri ,   ^c rj , ^c 6 i ’   ^c 6 j , ^c ri , ^c rj ,   ^T r 6 i ’   ^T r 6 j

( n > 1) из условиИ:

при

n — 0

^

при

n — 1

при

n >  1

<

^

с Г" ( r ) — c ri ’	, c ( r 1} ( r ) — c (1) ,
c. 1 ( r -) —c 6"	’ ce ) ( r , ) — c1'.
c rn 1 ( r i ) —c rn >	, c rn ) ( r , ) — c r; )
T r e ) ( r i ) —T r e i ,	T r e ) ( r j )—T r e ) •

,

Аналогично вычисляются коэффициенты A ⁽¹^ — A 4 ⁿ ) , n >  1.

После того как все выражения для базисных функции сформули рованы, реализуется метод конечных элементов в итерационной про цедуре метода геометрического погружения.

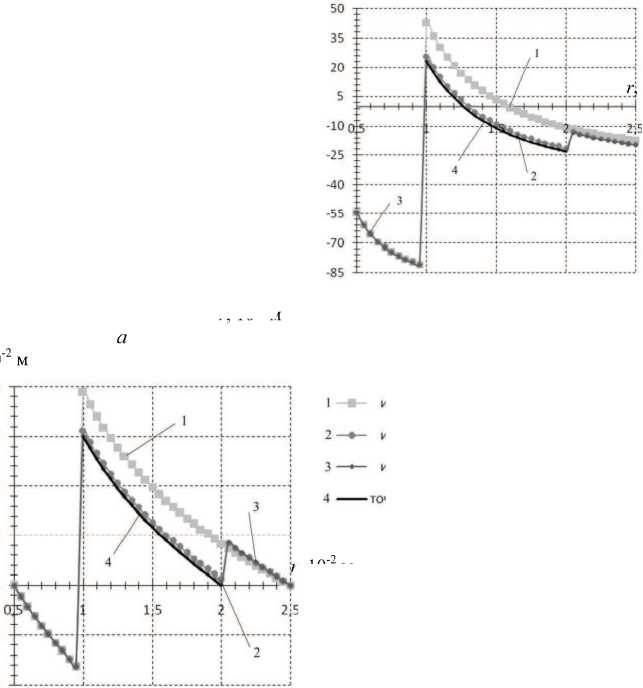
На рис. 10, 11 представлены результаты решения методом геометрического погружения для исходноИ области V при угле 6 — 0 , на рис. 12, 13 - для 6 —л/ 2 радиан. Из графиков прослеживается зависимость решения от окружной координаты. Относительная погрешность выполнения естественных граничных условиИ не превышает 0,56 %. Для каноническоИ области V 0 сетка содержит 60 элементов. Остановка итерационной процедуры происходит в соответствии с (13) при 5 — 10 ^{— 7}. Для достижения требуемоИ точности потребовалось 15 итерации.

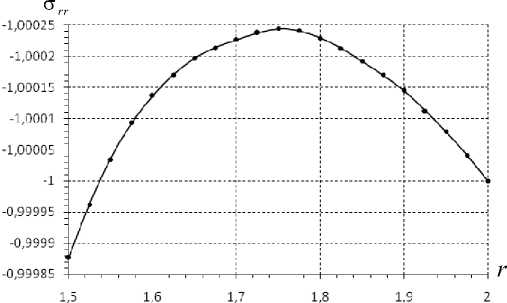
Рис. 10. Радиальные напряжения при 6 = 0

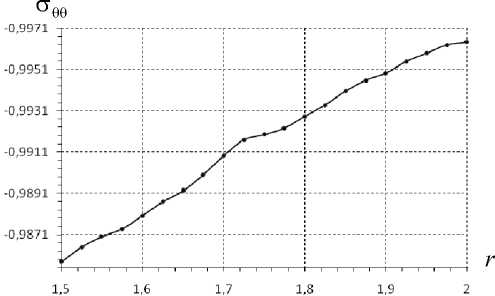
Рис. 11. Окружные напряжения при 6 = 0

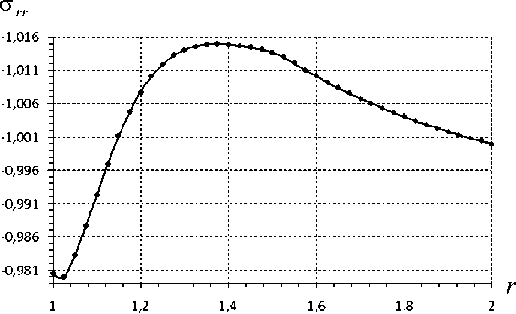
Рис. 12. Радиальные напряжения при 6 = л/2

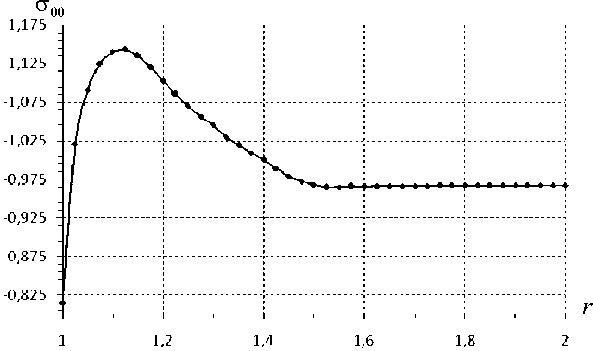
Рис. 13. Окружные напряжения при 0 = л/ 2

Таким образом, представлены результаты численного решения плоской задачи теории упругости для неканонической области, демонстрирующие практическую сходимость итерационной процедуры погружения, качество выполнения естественных граничных условий и характер распределения компонент тензора напряжений в области. Рассмотренный вариант метода геометрического погружения на основе вариационного принципа Кастильяно позволяет достигнуть высокой точности решения в напряжениях при достаточно небольшом числе элементов, эффективно решать задачи для конструкций неканонической формы в напряжениях.