Численно-аналитическое решение задачи оптимального управления

Современные вычислительные среды позволяют использовать как символьные, так и численные вычисления. При нахождении решения задач оптимального управления часто приходится проводить громоздкие символьные вычисления при сведении задачи оптимального управления к двухточечной краевой задачи. В данной статье рассмотрена автоматизация решения задачи оптимального управления с помощью вычислительной среды MathCAD, исходными данными для которой служит только постановка задачи.

Постановка задачи. Пусть задана система дифференциальных уравнений dx dX = f (x, u, t), x e Rm, dt                                     (1)

u e Rⁿ , t e [ t_n , t k ] ,

f(t, x):=

tn:= 0 tk:= 1 xn:

1+ x₁ 5

t • x 2 + u Г 1 "

xk:

Д"

Подынтегральная функция в критерии оптимальности (2)

F(x, u):= (2 • x ₀ )² + x 1 ² + u²

Эти операторы являются исходными данными в задаче оптимального управления. Следующий оператор сим-вольно вычисляет гамильтониан (3) (результат символьных вычислений здесь и далее справа от стрелки):

где x - состояние системы; u - управление; t - время; t_n , t k - начальное и конечное время. Необходимо перевести систему из начального состояния x ( t_n ) = xⁿ в конечное состояние x ( t_k ) = x k с минимальным значени-

- F(x,u)+

^{P 0}

L p i j

H(x, u, p):=

" ^T        .                   5

• ^f(t , x) ^ (u + t • x²) • P 1 +

^{+ (x}1⁺¹⁾ • Р о ^{- (2} • ^Хо^{) 2 - u}2

^^^^^™

x 1 ²

ем критерия оптимальности t k

I = j F ( x , u ) dt ^ min . t ^u

n

Следующие три оператора определяют структуру оптимального управления исходя из условия стационарности гамильтониана (5):

dHu:= H(x, u, p)

du

Для решения этой задачи составляют гамильтониан [1]

H = — F ( x , u ) + ( p • f ( x , u , t )) ,            (3)

где p - вектор сопряженных к вектору x переменных, и удвоенную систему двухточечной краевой задачи опти

мального управления

dx

— = f ( x , u , t ), dt

dp = d H dt       d x .

pp uopt:= dHu solve, u ^ -2 uopt ^ -2

В программах MathCAD невозможно выполнить символьное дифференцирование по индексной переменной d H x k , поэтому для вычисления частных производных--- ^{d x}k в записи гамильтониана приходится сделать подстановку

Для этой системы дифференциальных уравнений заданы n постоянных интегрирования x ( t_n ) = xⁿ на левом конце и n постоянных интегрирования x ( t k ) = x k на правом конце траектории x ( t ) . Для замыкания системы (4) применяют условие стационарности гамильтониана

с помощью оператора substitute вместо индексных переменных x 0 , x 1 простых переменных x 0, x 1 (по умолчанию нумерация в MathCAD начинается с нуля):

H:= H(x, u, p) substitute, x₀= x0,x 1 = x1 ^ u • p 1 + x1 p₀

- (2 • Х о )²

-

^в

-

u² - x1²+t • x0² • P 1 +P 0

= 0 ^ u ⁰( x , p ) d u

и, используя (5), исключают из уравнений (4) функцию управления u ( t ) .

Символьно-численная реализация алгоритма. Приведем реализацию алгоритма на примере нелинейной нестационарной системы второго порядка. Правые части дифференциальных уравнений (1), временной интервал,

п                           d H

Далее вычислим частные производные -- по про- dxk стым переменным, используя обратную подстановку:

dHx0:= ^d H dx0

dHx0:= dHx0substitute,

начальное и конечное состояние имеют следующую запись в системе MathCAD [2] (здесь и далее для записи операторов MathCAD используется прямой шрифт):

x0 = x₀, x1 = x 1 ^ t P2^{1 x} 0 - 8 • x 0

dHx1:= H dHx1:= dHx1 substitute, dx1

x0 = x₀,x1 = x 1 ^ p₀ - 2 - x 1

Теперь есть возможность вычислить правые части краевой задачи (4):

f(t, x)0

Fp(x):=

f(t, x)1

- dHx0

ния пройдут автоматически. Например, для задачи с начальными данными

_ . r^in(x 1 ^)+cos(x o ) f(t, x):= t*sin(x_o)+u

- dHxl

Fp(x):=Fp(x) substitute,

u = uopt ^

x1+1

t • x 2 + p i 0 2

⁸ • ^x 0 ^{- 5} • t • P l • ^xo ² • x l ^- P o

Для численного решения краевой задачи выразим правые части только через вектор х:

Fp(t, x):=Fp(x) substitute,

P o = ^x2 ,P i = ^x3 ^

⁸ • ^x o

x1+1

5x t • x2+— 02

5 • t • x 3 • x 2

^^^^^^.

2 • x₁ - x ₂

Итак, все готово для численного решения краевой задачи методом пристрелки. Для этого используем подпрограмму sbval, которая определяет недостающие начальные условия а для двух последних уравнений в (4), начиная с начального приближения v, после чего задача сведется к задаче Коши вместо двухточечной краевой задачи:

v:=

x:= stack(xn, v)

f1(tn,v):= stack(xn, v)

f2(tk,x):=

^xo ^{- xk}o x₁ - xk₁

a:= sbval(v,tn,tk,Fp,f1,f2) a=

- 32.113

- 1С.732

Интегрируем численно задачу Коши с известными

начальными условиями у на левом конце:

x ₀

a ₁

z:= rkfixed(y, tn, tk, 50, Fp) i:= 0..50

Получаем оптимальный процесс (рис. 1).

Обсуждение полученных результатов. Имея соответствующую программу, предложенную выше, пользователю для решения конкретной задачи с системой второго порядка необходимо набрать только условия задачи: правые части дифференциальных уравнений, интервал времени, начальные и конечные условия, а также критерий оптимальности (операторы (6), (7)). Далее как символьные, так и численные вычисле-

tn:= 0 tk:= 1 xn:

" 1 "

xk:

" 2 "

F(x, u):=u2

правые части системы получились следующими: Fp(t, x):=Fp(x) substitute, p0=x2,p1= cos(xo) + ln(x1)

t • sin(x o ) + X 3

= x₃ ^

sin(x_o) • x ₂ -

-

а оптимальный процесс представлен ниже (рис. 2).

t • cos(x_o) • x₃

x ₂

x1

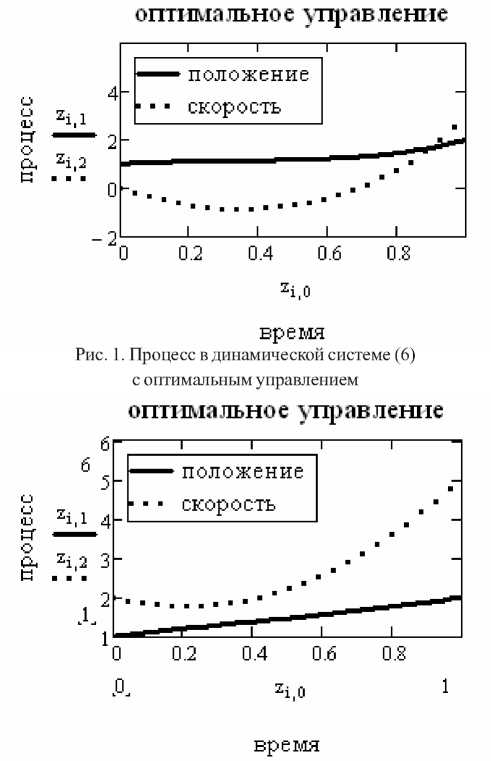
Рис. 2. Процесс в динамической системе (8), (9) с оптимальным управлением

Система более высокого порядка потребует больших размерностей векторов и введения дополнительных операторов для вычисления производных, аналогичных приведенным выше.

Следует иметь в виду, что далеко не каждая задача может быть решена предложенным выше способом. Первая

сложность может быть связана с тем, что программа символьного решения solve может не найти точного решения, особенно тогда, когда его нет. В этом случае придется дH искать решение уравнения — = 0 ^ u 0(x p) числен-д и но. Вторая сложность заключается в трудности решения краевой задачи программой sbval методом пристрелки. В этой программе происходит минимизация ошибки между требуемым и текущим положением системы в конечный момент времени за счет подбора начальных условий для сопряженных переменных p . Решение такой задачи часто зависит от выбора начальных значений v. Наконец, для нелинейных систем, в отличие от линейных, область решения не всегда принадлежит всему пространству Rn . Так, в системе (8) присутствует натуральный логарифм ln(x), что исключает значения x < 0 .

Современные вычислительные среды позволяют автоматизировать решение многих задач, требующих как численных, так и аналитических вычислений. Среда MathCAD является одной из наиболее приспособленных сред для решения таких задач.