Численно-экспериментальные методы определения параметров обобщенных моделей поврежденной вязкопластичной среды при прогнозировании долговечности

ВЕСТНИК ПНИПУ. МЕХАНИКА № 5, 2024PNRPU MECHANICS BULLETIN

Критически важные элементы энергетического оборудования и силовых установок работают в условиях сложного взаимодействия механизмов пластического деформирования. Прогнозирование долговечности подобных элементов основывается на модельных представлениях описания поведения деформируемой среды. Нелинейный отклик материала при статическом и циклическом деформировании связывают со смещением дислокаций и накоплением повреждений на микроуровне [1]. С точки зрения наиболее полных моделей, к которым можно отнести модели молекулярной динамики, современные вычислительные мощности не позволяют моделировать реальные элементы конструкций на мезомасштабном уровне [2]. В связи с этим совокупность происходящих на атомарном уровне процессов описывается в механике сплошной среды на основе энергетического баланса, связывающего внешние силы, приложенные к телу с деформационным откликом на мезоуровне. Такой подход требует для описания наблюдаемых зависимостей в сложных системах введение большого количества уравнений состояния исследуемой среды. Итоговая система уравнений в этом случае уже не просто не может быть решена аналитически, но даже и приближенные методы могут быть неприменимы ввиду отсутствия однозначного решения. В противовес этому, в инженерной практике предпочтение чаще всего отдается упрощённым моделям, которые могут в общих чертах с достаточной для конкретных задач точностью описать нелинейный отклик материала с существенным уменьшением требований к вычислительным ресурсам.

Наиболее эффективными при оценке характеристик сопротивления деформированию и разрушению при прогнозировании долговечности считаются методы, объединяющие экспериментальную механику сопротивления деформированию материалов и численное моделирование механизмов разрушения в виде соответствующих реологических моделей состояния среды. Переход материала в нелинейное состояние регулируется поверхностью текучести в пространстве главных напряжений [3–5]. В рамках поверхности текучести материал подчиняется закону Гука. Поведение материала за пределами поверхности текучести описывается с помощью аппроксимирующих экспериментальные данные функций. Накопление пластических деформаций или деформаций ползучести в подобных моделях может быть бесконечным. Ограничением тут будет выступать только сходимость приближенных методов. Декомпозиция деформаций обычно происходит на три составляющие – упругие, пластические и деформации ползучести. Такой подход наиболее прост в численной реализации и применяется повсеместно. В обобщенных моделях нелинейные деформации не разделяются на вязкие и пластические [6–8]. В подобных моделях в систему разрешающих уравнений вводятся законы накопления повреждений, описывающие кинематику измене- ния параметра поврежденности от действия усталостных нагрузок и нагрузок, вызвавших вязкое течение материала независимо друг от друга. Подробный литературный обзор современных моделей пластичности, разбор ограничений их применения и перспективы развития хорошо представлены в работе [9]. Усложнение подобных моделей для учета широкого спектра физически нелинейных задач приводит к необходимости решения довольно сложной системы нелинейных уравнений. И здесь на первый план выходят вычислительные ресурсы и проблемы с обеспечением сходимости решения при использовании приближенных методов [10]. Таким образом, в моделях, описывающих реологию среды, точность модели противопоставляется вычислительным ресурсам, необходимым для применения этих моделей к реальным элементам конструкции. Помимо этого, одним из ключевых недостатков классического подхода Работнова – Качанова является невозможность прогнозирования долговечности на стадии роста трещины ввиду зависимости от размерности сетки конечных элементов.

Последнее десятилетие широкое распространение в задачах прогнозирования остаточной долговечности конструкционных материалов получили модели фазового поля, в которых под фазовым переходом подразумевается переход от сплошного неповрежденного материала к разрушенному [11–15]. В основу метода фазовых полей разрушения заложен классический энергетический баланс Гриффитса, в который вводится наличие нелокальной области поврежденного материала. Такой подход позволяет разделять этапы интегрирования сложных систем дифференциальных уравнений при их решении методом конечных элементов. В данной работе моделирование процессов упругопластического деформирования и разрушения происходит путем объединения реологических моделей состояния физически нелинейной среды с моделями фазовых полей разрушения. Компиляция моделей реологии среды и моделей фазовых полей разрушения позволяет описать деградацию прочностных характеристик материала и достижение им критических состояний. При таком подходе наблюдается существенное упрощение применимости методов к оценке остаточной долговечности реальных элементов конструкций как с точки зрения численной реализации, так и с точки зрения вычислительных ресурсов.

Поведение поверхности текучести

В рамках допущений при описании среды принято, что материал изначально однороден и изотропен. Упругие деформации подчиняются обобщенному закону Гука. Переход материала в нелинейное состояние регулируется поверхностью текучести в пространстве главных напряжений. Для описания изменения радиуса поверхности текучести используется трехпараметрическое экспоненциальное уравнение, предложенное Voce:

R = C o + R o _s eqv + R inf ■ [ 1 - exp( -y_E q ) ] ,       (1)

где £ eqV - эквивалентные пластические деформации, c ₀ -предел текучести материала, R ₀ – линейный параметр упрочнения, R _inf – асимптотический предел временного сопротивления, у - показатель упрочнения материала.

Смещение центра поверхности текучести в пространстве главных напряжений моделируется на основе подходов, изложенных в работах Chaboche и получивших развитие в работах множества других авторов [16– 18]. Для описания кинематики обратных напряжений используется уравнение Armstong – Frederik [19]:

e ⁽ n) = 3 a ⁽ n ) £ pl - b ⁽ n ) e ⁽ n ) £ eqv ,

где β(n) – тензор девиатор обратных напряжений, a(n) и b(n) - константы материала, £pl - тензор скоростей

2ll пластических деформаций, £ q = Jy £ pl £ pl - скорость накопленной пластической деформации. Количество уравнений для удовлетворительного описания кинематики обратных напряжений обычно не превышает n = 3. Итоговый тензор обратных напряжений представлен суперпозицией n тензоров обратных напряжений:

n в = E в(i).

i = 1

Вязкий отклик материала в нелинейной области выражается через связь эквивалентных напряжений по Мизесу и скоростей эквивалентных деформаций и задается через классический степенной закон второй стадии ползучести Нортона:

- c

£ ^eqv = B c m e T cr eqv

где В , С и m – константы характеризующие свойства материала, Т – температура по шкале Кельвина.

Форма поверхности текучести

В случае многоосного нагружения размер поверхности текучести может быть непостоянен в пространстве главных напряжений. Сочетание уравнений (2) и (3) приводит к быстрой стабилизации петли упругопластического гистерезиса и не способно описать одностороннее накопление деформаций в процессе циклического деформирования. Распространена практика, когда подобное поведение материала описывается различными сценариями в зависимости от знака нагружения. Подходы, заложенные в работах Писаренко – Лебедева [20], когда форма предельной поверхности корректируется с помощью функции, характеризующей отношение прочностных характеристик при растяжении и сжатии, позволяют избежать необходимость введения дополни- тельных сценариев при многоосном нагружении. Предложенные подходы получили очень широкое распространение и развиваются до сих пор. Для описания формы поверхности текучести использованы зависимости, предложенные в работах [21; 22]. Согласно данному подходу, сочетание параметра трехосности и параметра Lode может однозначно идентифицировать вид многоосного нагружения. Следует отметить, что в данной работе используется формулировка параметра Lode, отличающаяся от классической, а именно:

иметь вид параболы k -го порядка с фокусом на оси ординат и будет чувствительна только к абсолютным значениям соотношения главных напряжений.

27./.

L = - cos30, =--^,

^L     2 a ³

eqv

где 0 _L - угол Lode, J 3 = a 1 -0 2 -0 3 - третий инвариант тензора напряжений, a i - главные напряжения. Связь с

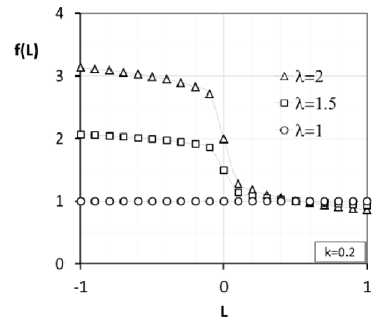
Рис. 1. Зависимость функции f ( L ) от параметра Lode

Fig. 1. Dependence of the function on the Lode parameter

классической формулировкой параметра Lode

ц = (2 а 1 -о ₃ - a ₂) / ( a ₃ - a ₂) выражается в следующем

виде [23]:

L = ц(9-ц2)Дц2 + 3)3 .            (6)

Тогда функция зависимости предельных деформаций от угла Lode при монотонном статическом деформировании, согласно [24], выразится в следующем виде:

f (L ) = X + (1 -X)

' 2

— arccos

пк

' 27 J 3 2 а ³ к eqv

ЛАк

X = f ⁰ . ⁵ / s ^x;° ,

х =

а2

-а3

а1 -а3

где к - параметр формы кривой, X - свойство материала, выраженное через отношение предельных деформаций при х = 0,5 к предельным деформациям при

X = 0 в условиях одинакового гидростатического давления. Уравнение (7) в составе системы позволяет направлять вектор смещения поверхности текучести при кинематическом упрочнении, что, в свою очередь, позволяет не только описать эффект одностороннего накопления пластических деформаций при циклическом нагружении, но и прогнозировать поведение материала при сложном напряженном состоянии.

На рис. 1 представлены значения функции учета локальной многоосности от параметра Lode. При значениях L <  0,5 данная функция будет уменьшать радиус поверхности текучести, а при L >  0,5 - увеличивать. Предлагается значения параметра k выбирать из следующего ряда к = 1/5,1/3,1,3,5.... Избавление от модуля в знаменателе функции хоть и ограничивает выбор значений параметра k , однако дает возможность заложить разницу предельных состояний при растяжении и сжатии. При четных значениях параметра k функция будет

Фазовые поля разрушения

Как уже было отмечено ранее, классический подход механики поврежденной среды, основанный на параметре поврежденности Работнова – Качанова не позволяет охватить все стадии прогнозирования долговечности без применения методов адаптивного построения конечно-элементных моделей. Даже наиболее продвинутые методы не избавляют от влияния размерности конечно-элементной модели на полученные результаты [25]. В данной работе процесс накопления внутренних повреждений описывается не с точки зрения кинематических законов их эволюции, а с точки зрения энергий, необходимых для роста микроповреждений на основе фазовых полей разрушения. В моделях фазовых полей разрушения предполагается, что разрушение происходит не локально, а в некоторой области вершины трещины (рис. 2). Вводится вспомогательная фазовая переменная поврежденности φ. Если классический параметр поврежденности обычно рассматривают как отношение площадей повреждений к начальной площади в бесконечно малом объеме, то в моделях фазового поля параметр поврежденности удобно воспринимать как плотность трещин в рассматриваемой точке. Как и в случае параметра поврежденности Работнова – Качанова, при φ = 0 материал не имеет повреждений, а при φ = 1 материал считается полностью разрушенным в рассматриваемой точке. Данная переменная вблизи поверхности трещины аппроксимируется экспоненциальной функцией [26]:

- И ф ( и ) = e I .

Функционал, характеризующий наличие трещины внутри рассматриваемого контура Q, представлен в следующем виде

^Г l ( ф ) = Jj( 9 , Уф ) dV ,             (10)

где y - скорость высвобождения энергии. Тогда энергия, необходимая для образования новой поверхности раздела в энергетическом балансе Гриффитса [27]

У = G c d_css * J g f 1ф ² + ¹ | 7ф |² 1 dV ,    (11)

Г'          QI2 l 2 J где Gc – критическое значение скорости высвобождения энергии. Основные разрешающие уравнения фазовых полей разрушения выводятся из удовлетворения баланса виртуальной работы внешних (5 Wext) и внутренних (5 Wnt) сил:

d W nt -д W ext = 0.               (12)

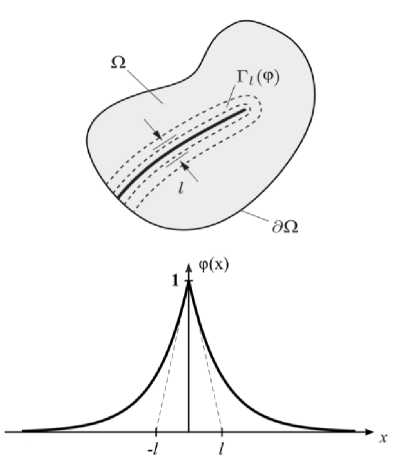
Рис. 2. Представление трещины в моделях фазовых полей разрушения

Fig. 2. A a crack in models of phase fields of destruction

Если функция деградации свойств материала представлена в виде g ( ф ) = (1 -ф ) ² , то с учетом (11) внутренняя энергия, затрачиваемая на деформирование и продвижение трещины:

^S W int

= Г [а: Зе - 2(1 -ф)Зфф(Е) + Gc 1 ф8ф +1 Уф-УЗф dV ,(13) qi                                      cl                         J где у (е) = у ei (е) + у pi (е) + у cr (е) - сумма упругой, пластической и вязкой плотностей энергии деформации.

Работа внешних сил является суммой работ объемных сил b и сил h , приложенных к границам области SQ h :

3 W ext = J _q b ' 3 u dV + J _sq h h ■ 3 u dA .       (14)

Применение теоремы Остроградского – Гаусса позволяет получить основное уравнение баланса в задаче фазовых полей разрушения. Согласно данной теореме, поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность равен интегралу от дивергенции этого поля по объёму, ограниченному этой поверхностью [28]. В итоге получается следующее разрешающее уравнение:

J q ( - [ Div[ a ] + b ] ■ 3 u -

- 2(1 -ф ) у ₀( Е ) + G_c 1 1 ф- Div [ l Уф]^ 3ф^ dV + (15)

+   [o^n-h]^3udA +    [GlУф^п]^3фdA = 0, q                sq h где n - вектор нормали к поверхности SQ .

Численная реализация

Вязкоупругопластичность

Для описания вязкоупругопластичной среды в рамках численной реализации физически нелинейного материала используется стандартная декомпозиция деформаций на упругую и пластическую деформацию, а также деформацию, вызванную ползучестью:

^Е = ^Е el ^{+ Е} pl ^{+ Е} cr .                     ⁽¹⁶⁾

В общем виде критерий текучести записывается в виде

Ф( а , $ = 0,                   (17)

где £ - представляет собой набор скалярных и/или тензорных переменных, связанных с историей нагружения. В данной реализации уравнение поверхности текучести с учетом (2)–(4) примет следующий вид:

Ф = 2 ( s - в ) : ( s - в ) - R ² = 0,           (18)

где s – девиатор тензора напряжений; β – девиатор тензора обратных напряжений, представляющий собой термодинамическую силу, связанную с кинематическим упрочнением, и определяющий перемещение поверхности текучести в пространстве главных напряжений; R – функция изотропного упрочнения, которая определяет радиус поверхности текучести (1).

Накопление пластических деформаций определяется законом течения:

S Q„, dеpl = d 9pl^,              (19)

да где d9 - бесконечно малый скалярный множитель, Qpl -пластический потенциал.

Накопление деформаций ползучести определяется с помощью потенциала Q_cr , при этом выполняется (4):

ε

cr

= 9

cr

Q д о

Интегрирование по области производится с помощью метода конечных элементов. Расчеты выполнены в комплексе программ ANSYS. Описанные модельные представления реализованы в виде динамически подключаемой библиотеки пользовательского материала (USERMAT). Авторские исходные коды программ и инструкции по компиляции и подключению созданных динамических библиотек находятся в свободном доступе [29].

Фазовые поля разрушения

тогда соответствующий ему вектор узловых сил должен быть

{ r } = ^{ r u 1 , r v 1 , r 1 ... r u 4 , r v 4 , ^Г Ф 4 ^{} Т} .              ⁽²⁵⁾

Таким образом, для интегрирования в систему расчетов ANSYS необходимо упорядочить компоненты матрицы жесткости элемента в следующем виде:

	u 1 K ru 1	v 1 K ru 1	0.	u 4 .. K ru 1	v 4 K ru 1	0 ]
	u 1 K rv 1	v 1 K rv 1	0.	u 4 ..    K rv 1	v 4 K rv 1	0
	0	0	К ф 1 Kr ф 1 .	..0	0	к ф 4 Kr ф 1
[K] =	u 1 K ru 4	v 1 K ru 4	0.	u 4 ..   K ru 4	v 4 K ru 4	0	.(26)
	u 1 K rv 4	v 1 K rv 4	0.	u 4 ..    K rv 4	v 4 K rv 4	0
	_ 0	0	К ф 1 r ф 4 .	..0	0	к ф 4 л r ф 4 _

Фазовое поле рассматривается как дополнительные степени свободы. В простейшем двухмерном случае можно заменить степень свободы узла u_z на параметр фазового поля φ.

В основу разрабатываемого конечного элемента был положен линейный изопараметрический элемент. Используя нотацию Фойгта для двухмерного пространства поле смещений, u = { u , v } T и фазовое поле по-врежденности φ (9) может быть дискретизировано через функции формы элемента:

mm u = Е Niui и ф = Е NA , i=1

где N i - функции формы, u i = { u i , v i }^T , m - количество узлов элемента. Тогда:

mm e = Е BUui и Vф = Е B Ф Vi,(22)

i=1

где e = { s xx , s yy , s xy } - вектор деформаций. Матрица, связующая деформации и перемещения:

Для элементов более высоких порядков структура представленных матриц будет подобной. Элементы данной матрицы для степеней свободы u_i и v_i вычисляются по следующим уравнениям:

K j = J g ( Ф ) ■ ( B u ) ^T C o B uj dV ,

, Q                                (27)

r u = J g ( Ф ) ■ ( B u ) ^T о dV ,

Q

а для степени свободы, характеризующей фазовое поле

разрушения

K ^ф = jK2 _{V o} + G c I N.N . + G_c ■ l ■ B T B . \dv , Й tv           l J                          J

Г ^Ф = J 1 2(1 — Ф ) V o N i + G c [ф N i + 1 2 ( B i ) T Vv]| dV . Q I                        ^{l                              J}

Для решения задачи методом конечных элементов необходимо привести систему разрешающих уравнений к следующему виду:

[ K g ] { " g } = { r g 1 •                  (29)

b u =

N i , x 0

0 N i , y

N i , y N i , x

and

N i , x

N i , y

где K g - глобальная матрица жесткости, { u g } - глобальный вектор степеней свободы и { r g } - глобальный вектор узловых сил. После процесса сборки полученная система уравнений решается итерационно методом Ньютона – Рафсона:

где N_{i , x} и N_{i , y} производные функций формы в каждом узле в системе координат элемента.

Как уже было отмечено ранее, реализация представленной методологии производилась в конечно-элементном комплексе ANSYS. Далее приведен пример реализации линейного изопараметрического элемента. В соответствии с документацией вектор перемещений элемента должен быть представлен в следующей форме:

{ u } = { u 1 , V 1 , Ф 1 ... u 4 , v 4 , Ф 4/ ,              (24)

¹¹ g L. = { ■ g } + ^{[ K} g 1 -' { ' g 1 .          (³⁰⁾

При решении этой системы достижение сходимости подразумевает достижение равновесного состояния. Реализация метода в общей трехмерной постановке полностью идентична, меняется только размерность матриц. Как и в случае пользовательского материала, элемент, реализующий фазовые поля разрушения, был интегрирован в расчетный комплекс через возможность подключения к ANSYS созданного пользователем элемента (USERELEMENT) [29].

Экспериментальные исследования

Основной целью обработки экспериментальных данных циклического нагружения являлось выявление физических процессов, происходящих в результате малоциклового деформирования в каждой отдельной петле упругопластического гистерезиса. Были проведены исследования поведения двух типов конструкционных материалов при малоцикловом нагружении – сталь Р2М и титановый сплав ВТ6. Испытания проводились при постоянной амплитуде нагружения с коэффициентом асимметрии гармонического цикла R^sym = -1 . Для титанового сплава ВТ6 также были проведены испытания при коэффициенте асимметрии цикла R sm = 0,1, включающие в себя испытания при трапециевидном цикле нагружения с выдержкой под нагрузкой в течении 120 секунд (рис. 3).

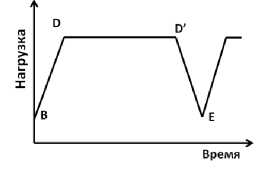
Рис. 3. Трапециевидный цикл нагружения

Fig. 3. Trapezoidal loading cycle

Таблица 1

Результаты испытаний на малоцикловую усталость

Table 1

Low-cycle fatigue test results

Материал	Уровень напряжений σ n , МПа	Коэффициент асимметрии, R sym	Выдержка под нагрузкой, с	Долговечность, N f
Р2М	375	-1	Без выдержки	20200
	425			8177
	450			4601
	500			2004
ВТ6	800			2181
	850			1486
	900			818
	890	0,1		15094
	950			8155
	1000			3246
	850		120	5870
	900			950
	950			372

Уровни напряжений, при которых проводились испытания, и полученные значения долговечности занесены в табл. 1. Все испытания проводились при комнатной температуре (20 °С).

Определение параметров модели

При проведении испытаний производилась запись каждой петли упругопластического гистерезиса. В цик- лических испытаниях на первых циклах нагружения металлических сплавов в большей или меньшей степени можно наблюдать существенное уменьшение ширины упругопластического гистерезиса. Это обусловлено ростом зоны пластических деформаций и соответственно резким уменьшением радиуса поверхности текучести. На последующих циклах нагружения можно наблюдать эффект стабилизации ширины упругопластического гистерезиса. Этот эффект невозможно описать классическими моделями изотропного упрочнения (Voce, Ramberg – Osgood и т.п.), так как данные модели предполагают одностороннее увеличение уровня напряжений при увеличении уровня пластических деформаций. При попытке описать эффект резкого изотропного разупрочнения материала в начале циклического нагружения с его последующим упрочнением аппроксимирующими функциями наличие экстремума делает невозможным однозначное решение задачи интегрирования приближенными методами. Данная особенность поведения материалов при циклическом деформировании вносит неоднозначность в процедуры определения параметров моделей, используемых для описания реологической среды. Один и тот же результат при прогнозировании долговечности на основе сложных обобщенных моделей может быть достигнут при различном сочетании ее параметров. Однозначность параметров модели для исследуемых материалов может быть достигнута только фиксацией алгоритмов их определения.

Определение параметров модели осуществлялось в следующей последовательности на примере стали Р2М. На первом этапе для каждого уровня номинальных напряжений необходимо провести анализ изменения ширины упругопластического гистерезиса и выбрать условно стабильный цикл нагружения.

0.01

АеР

0.008

0.006

0.004

0.002

N/Nf

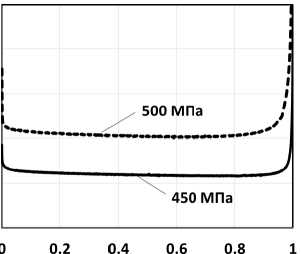
Рис. 4. Изменение ширины упругопластического гистерезиса в процессе малоциклового деформирования

Fig. 4. Change in the width of elastic-plastic hysteresis during low-cycle deformation

В связи с тем что при циклическом упрочнении без учета накопления внутренних повреждений модельные представления приведут к тому, что ширина петли гистерезиса будет стремиться к нулевому значению, в качестве стабильного цикла нагружения предлагается выбирать цикл с минимальной шириной петли упруго- пластического гистерезиса (рис. 4). Для данного цикла можно считать, что материал изотропно упрочнился и пренебречь дальнейшим изменением радиуса поверхности текучести. После выбора условно стабильных петель гистерезиса подбираются параметры уравнений (2)–(3). На следующем этапе подбираются параметры уравнения (1) таким образом, чтобы обеспечить совпадение ширины петли первого и условно стабильного циклов нагружения. В этом случае модель, хоть и будет давать большую погрешность на первых циклах нагружения, однако описание поведения материала в общем диапазоне долговечности будет удовлетворительным. Также здесь необходимо учитывать два взаимосвязанных процесса, по-разному влияющих на петлю упругопластического гистерезиса. С одной стороны, размах пластических деформаций при изотропном упрочнении будет стремиться к нулевому значению и с каждым циклом нагружения ширина петли будет уменьшаться. С другой стороны, модель фазовых полей разрушения обусловливает накопление внутренних повреждений и деградацию свойств мате- риала, которые в свою очередь, наоборот, приводят к расширению петли упругопластического гистерезиса. Косвенно об уровне накопленных повреждений можно судить из анализа изменения модуля упругости при растяжении/сжатии на каждом цикле нагружения. Анализ изменения упругих свойств материала может существенно упростить выбор уравнений деградации свойств материала.

Далее подбираются параметры уравнения (7) для описания одностороннего накопления деформаций и эффекта вышагивания петли упругопластического гистерезиса (рис. 5).

На заключительном этапе определяются параметры модели фазовых полей разрушения. В первом приближении критическое значение скорости высвобождения энергии принято равным площади под кривой одноосного деформирования, и варьировалось значение структурного параметра l для обеспечения совпадения прогнозируемой и экспериментально полученной долговечностей. Определенные таким образом параметры модели представлены в табл. 2.

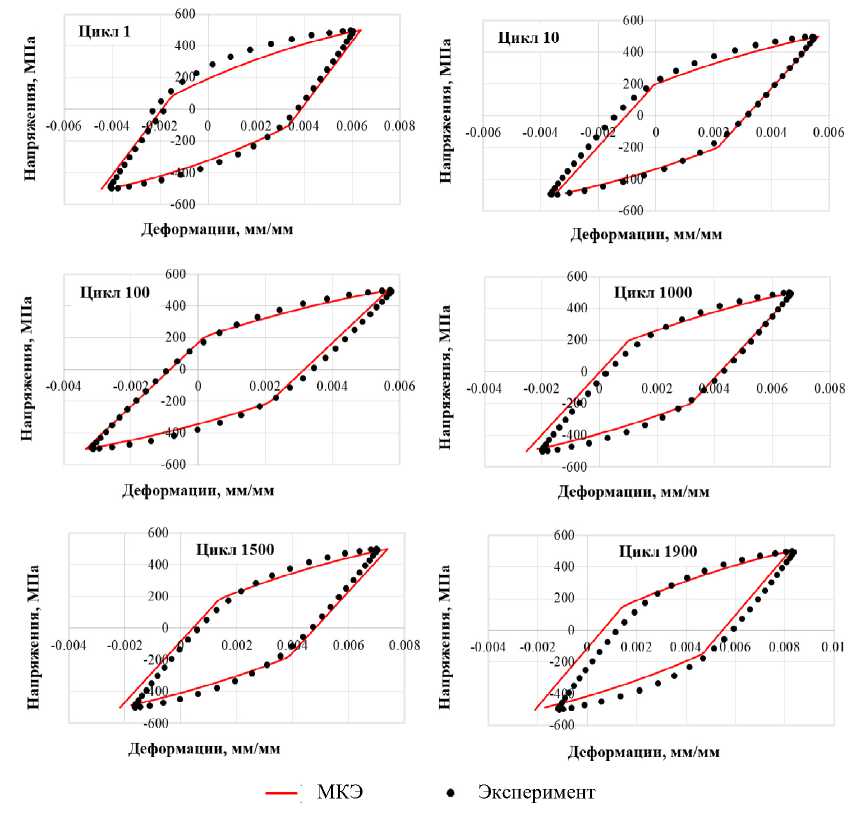
Рис. 5. Прогнозирование поведения петель упругопластического гистерезиса при мягком нагружении стали Р2М

Fig. 5. Prediction of the behavior of elastic-plastic hysteresis loops under soft loading of P2M steel

Таблица 2

Параметры модели

Table 2

Parameters of the model

Материал	Модуль упругости	Коэффициент Пуассона	Предел упругости	Параметры изотропного упрочнения (1)			Параметры кинематического упрочнения (2)		Параметры ползучести (4)		Параметры формы поверхности текучести (7)		Параметры модели фазовых полей (15)
	Е	ν	σ 0	R 0	R inf	γ	a	b	B	m	λ	k	l	G c
Сталь Р2М	210	0,3	49	5	228	1002	117 500	500	-	-	0,99	1	4	12 000
Титан ВТ6	132	0,3	402	470	502	5	280 000	410	1,38e-41	19,9	0,99	1	3,7	26 100

Численные расчеты

В данном исследовании приведены результаты решения задач прогнозирования долговечности цилиндрических образцов в двухмерной осесимметричной постановке. Размерность сетки конечных элементов определялась моделью фазовых полей разрушения, которая требует наличия минимум 8 элементов на характерном размере l . Шаг интегрирования определялся из условий приближения полученных результатов к асимптотическому пределу с заданной точностью в 1 %. Моделировалась только рабочая цилиндрическая часть образца без учета расширяющейся части. В связи с очень низкими скоростями деформаций в период выдержки под нагрузкой при комнатной температуре, а также ограничением памяти на хранение переменной типа double precision в языке программирования Fortran, за единицу времени в расчетах, учитывающих вязкое течение, принято: 1 с равна 10^–6 усл. ед.

В результате проведенных виртуальных экспериментов на основе вышеописанных алгоритмов определения параметров модели были получены кривые долговечности для стали Р2М при мягком нагружении (рис. 6).

га

| 650

! 550

I 450 x

■   • Эксперимент

: ■ МКЭ

100         1000        10000

Количество циклов, N

Рис. 6. Кривая долговечности стали Р2М при осесимметричном цикле нагружения

Fig. 6. Durability curve of P2M steel under axisymmetric loading cycle

■□

О■ □

•CO[

О» О ♦

• •    R=-l о •

• ■    R=0.1

• ♦    R=0.1 с выдержкой 120 с

  200              2000             20000

Количество циклов, N

Рис. 7. Кривые долговечности титанового сплава ВТ6 при циклическом нагружении

Fig. 7. Durability curves of titanium alloy VT6 under cyclic loading

Для титанового сплава ВТ6 экспериментальные результаты и результаты виртуального эксперимента представлены на рис. 7. Закрашенные точки соответствуют экспериментальным данным, незакрашенные – виртуальному эксперименту при идентичных условиях.

Обсуждение

В литературе широко распространены модели, описывающие нелинейную связь между деформациями, напряжениями и внутренней поврежденностью. Для описания сложного взаимодействия нелинейных процессов, как правило, формируется система разрешающих уравнений, описывающих совокупность и взаимовлияние таких феноменологических и физических явлений, как изотропное упрочнение, кинематическое упрочение, вязкопластичность (ползучесть), а также накопление и развитие повреждений. Каждая из подобных обобщенных систем уравнений имеет свои уникальные методы определения входящих в нее параметров, зависящие от конкретного набора уравнений, входящих в систему. Более того, методология определения параметров часто бывает применима только для заранее определенной системы разрешающих уравнений. При исключении одного уравнения из системы методы определения параметров обобщенных моделей будут нуждаться в корректировке. Предлагаемая в данной работе комплексная методология ставит одной из целей разработку таких методов, которые бы позволяли определять параметры отдельных моделей, входящих в итоговую систему уравнений без привязки к определенному сочетанию конституционных уравнений, но с привязкой к механическим свойствам материала. Предложенные методы будут оставаться справедливы также и при изменении набора конституционных уравнений.

Проведенные исследования показали, что предлагаемый подход позволяет с удовлетворительной точностью виртуально воспроизвести экспериментальные исследования поведения металлических материалов при малоцикловом деформировании и взаимодействии усталости и ползучести. Следует отметить, что описанный метод определения представленного набора параметров требует глубокого понимания принятых допущений и степени их влияния на поведение моделируемой среды. В описанном методе предлагается использовать измеряемые экспериментально величины при определении характеристик многопараметрических моделей, однако в некоторых случаях несущественное отклонение от экспериментально определенных значений может существенно повысить точность прогнозирования и существенно расширить диапазон применимости модели. В связи с тем что подобных корректировок не производилось, представленные в табл. 2 параметры справедливы только в рассматриваемых диапазонах долговечностей и уровнях действующих напряжений. При расширении диапазона нагрузок (особенно при уменьшении уровня действующих напряжений) упрощенное описание поведения материала на начальном этапе циклического деформирования может привести к существенным ошибкам в оценке прогнозируемой долговечности.

При подборе параметров в моделях пластического течения следует уделить особое внимание определению предела перехода от линейного состояния к нелинейному. Проведенные исследования показывают, что значения радиуса поверхности текучести для подобных обобщенных моделей в большинстве случаев оказываются кратно меньше условного предела текучести, ко- торый часто используется в качестве константы материала, используемой в роли триггера перехода в физическую нелинейность. Также необходимо отметить, что монотонно возрастающая функция типа (1) изначально не может обеспечить корректное описание поведения петель гистерезиса на протяжении всего периода долговечности при малоцикловом деформировании. Для корректного описания необходимо вводить функцию, в которой допускается изменение знака первой производной на рассматриваемом участке пластических деформаций. Автору неизвестны успешные численные реализации подобных функций. Авторы работы [30], проанализировав поведение различных материалов, также приходят в выводу, что теория деформационного упрочнения не может на 100 % качественно описать экспериментально наблюдаемую феноменологию. Данные особенности необходимо учитывать при использовании представленных алгоритмов в целях прогнозирования долговечности реальных элементов конструкций.