Численно-статистический метод для решения задач теплообмена в теплозащитных конструкциях сотового типа
Автор: Гусев С.А., Николаев В.Н.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 4 т.18, 2017 года.
Бесплатный доступ
Предложен метод для определения теплового состояния теплозащитной панели сотового типа. Примене- ние теплозащитных материалов такого типа является перспективным направлением при конструировании высокоскоростных летательных аппаратов. Рассматриваемый процесс переноса тепла описывается краевой задачей для уравнения теплопроводности. При этом предполагается, что коэффициенты температуропро- водности материалов, из которых состоит панель, являются постоянными величинами, а процесс передачи тепла осуществляется только посредством теплопроводности. Предложенный метод основан на вероятно- стном представлении решения краевой задачи в виде математического ожидания от функционала случайного процесса диффузионного типа и численном моделировании этого случайного процесса. В более ранних рабо- тах предлагалось проводить вычисления с использованием метода Эйлера. В связи с тем, что процесс тепло- обмена происходит в неоднородной среде, при численном моделировании траекторий случайного процесса ис- пользуется сглаживание разрывных коэффициентов уравнения теплопроводности на основе интегрального усреднения. При этом в подобластях, в которых среда однородная, моделируемый случайный процесс является винеровским. Этот факт означает, что значительного ускорения счёта можно достичь путем использования в этих подобластях метода случайного блуждания по сферам. Предлагается для моделирования винеровского процесса внутри ячеек сотовой панели использовать метод блуждания по сферам, а для расчётов по каркасу панели и в его окрестности - метод Эйлера. Проведённые расчёты по данным физического эксперимента показали значительную эффективность предложенного комбинированного метода по сравнению с вычисле- ниями только одним методом Эйлера.
Сотовая панель, задача теплообмена, вероятностное представление, численно- статистическое моделирование, винеровский процесс, метод эйлера, метод блуждания по сферам
Короткий адрес: https://sciup.org/148177753
IDR: 148177753 | УДК: 51-74
Текст научной статьи Численно-статистический метод для решения задач теплообмена в теплозащитных конструкциях сотового типа
Введение. При конструировании авиационной и космической техники важнейшее значение приобретает устройство тепловой защиты летательных аппаратов. Одним из возможных вариантов решения этой проблемы является применение теплозащитных панелей сотового типа [1–5]. Сотовая теплозащитная панель представляет собой конструкцию, состоящую из параллельно расположенных пластин, между которыми заключен тонкий каркас в виде пчелиных сот, заполненных некоторым веществом с низкой теплопроводностью. Основными преимуществами таких средств тепловой защиты являются хорошие теплофизические свойства и небольшой вес при относительно невысокой стоимости и достаточной прочности. Данная статья посвящена математическому моделированию процессов теплообмена в таких теплозащитных конструкциях и разработке метода расчёта для определения их теплового состояния в реальных условиях.
В работе [6] для расчёта теплопереноса в сотовой панели предлагался численно-статистический метод, основанный на вероятностном представлении решения краевой задачи для уравнения теплопроводности и численном решении стохастических дифференциальных уравнений (СДУ). При этом делалось сглаживание разрывных коэффициентов уравнения теплопроводности на основе интегрального усреднения, а численное решение СДУ осуществлялось методом Эйлера.
С помощью метода Эйлера возможно получение хороших статистических оценок решения уравнения теплопроводности, но большая трудоёмкость такого подхода даже при хорошей возможности распараллеливания и применении суперкомпьютерной техники не позволяет проводить реальные расчёты для достаточно больших интервалов полётного времени.
С другой стороны, если теплофизические свойства материалов, из которых состоит сотовая панель, незначительно изменяются в рассматриваемом диапазоне температур и внутри панели отсутствуют источники тепловой энергии, то возможна модификация алгоритма расчёта, позволяющая значительно уменьшить вычислительные затраты. Действительно, если коэффициенты температуропроводности материалов сотовой панели постоянны, а передача тепловой энергии внутри панели осуществляется исключительно теплопроводностью, то случайный процесс в однородной среде, который присутствует в вероятностном представлении, есть ни что иное, как винеровский процесс. Точка первого выхода винеровского процесса на границу шара имеет на ней равномерное распределение.
Следовательно, при моделировании траекторий винеровского процесса в подобластях с однородной средой можно двигаться не по траекториям, которые получаются методом Эйлера, а по границам шаров, находящихся в этих подобластях. В этом состоит основная идея метода случайного блуждания по сферам [7]. Но при решении нестационарных задач требуется помимо точки первого выхода винеровского процесса на границу шара ещё моделировать время первого достижения границы шара. Как известно [8], распределение времени первого выхода винеровского процесса на границу шара совпадает с распределением времени первого достижения уровня, равного радиусу шара, одномерным бесселевским процессом. Но плотность времени первого достижения бесселевским процессом заданного уровня выражается сложной формулой в виде ряда, содержащего функции Бесселя первого рода и их положительные нули. По этой формуле очень затруднительно построить эффективный алгоритм для моделирования времени первого выхода. С другой стороны, вместо заданного уровня, который требуется достичь, можно подобрать некоторые кривые [9], зависящие от t , такие, что получаются достаточно простые и удобные для моделирования формулы для плотности времени первого достижения бесселевским процессом этих кривых. Этот метод используется в данной работе, и он называется блужданием по движущимся сферам.
В качестве области изменения пространственных переменных x1 , x2 , x3 в работе принимается прямоугольный параллелепипед G = (-11,11) х (-12,12) х (0,13). При этом G есть объединение двух непересекающих-ся подмножеств: G = G1 и G2, где G1 - подобласть, соответствующая каркасу и пластинам, ограничивающим панель, а G2 есть объединение подобластей, соответствующих ячейкам, содержащим теплоизоляционный материал. Каждая ячейка представляет собой внутренность правильной шестиугольной призмы, боковая поверхность которой параллельна оси x3 . Предполагается, что рассматриваемый процесс теплопередачи происходит на отрезке времени [0,T] и описывается следующей краевой задачей для уравнения теплопроводности:
dи д Г, , . ди )
= / I b ( x ) I ,
д t i=1 дx l дx J где b (x) =
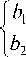
x e G 1
x e G 2’
u ( x ,0) = Ф( x ), (2)
д u д x1
x i =- l 1
— 0, ^
д x 1
— 0, x 1 — l 1
дu дx 2
— 0, u x 2 —— 1 2 5 x 2
— 0, x 2 — 1 2
X — дx3 n
-
3 x 3 =0
. д u
—X— дx3 x.-l x
= ai( t ) ( u - v ( t ) ) ,
= a2 ( t ) ( u — V 2( t ) ) .
В (1)–(6) использованы следующие обозначения: φ – начальное распределение температуры в панели; λ – коэффициент теплопроводности углепластика; b1 , b2 – коэффициенты температуропроводности углепластика и воздуха соответственно; α1 , α2 – коэффициенты теплообмена между панелью и внешней средой; ψ1 , ψ2 – температура внешней среды у нижней и верхней сторон панели соответственно.
Сглаживание коэффициентов . Поскольку теплозащитная панель состоит из двух материалов с различными теплофизическими свойствами, то в задаче (1)–(6) мы имеем уравнение теплопроводности с разрывным коэффициентом температуропроводности. Достаточно полное математическое исследование краевых задач для параболических уравнений с разрывными коэффициентами дано в книге [10]. Там же приведены условия существования и единственности обобщенного решения (теорема 5.1, гл. III) в пространстве функций P 2 0,1( Q T ) ( Q T — G x (0, T ) ) , обладающих
T—h свойством J J h—1(u (x, t + h) — u (x, t))2dxdt ^ 0
0G при
h ^ 0 , с нормой
I “ k — max I| u ( x , t )IL
Q T 0< t < T L 2 ( G )
^ ) 2
J u x dxdt .
V О т
Как утверждается в [10] (теорема 4.5, гл. III), обобщенное решение краевой задачи с разрывными коэффициентами в параболическом уравнении в норме пространства Р 2 0,1 ( QT ) устойчиво относительно вариаций коэффициентов. Из этой теоремы применительно к задаче (1)-(6) следует, что если при m ^да равномерно ограниченная последовательность b ( m ) сходится почти всюду к b , тогда обобщенные решения задач с коэффициентами b ( m ) сходятся сильно в норме k,1 ( Q T ) к обобщенному решению задачи (1)-(6).
Таким образом, при достаточно больших значениях m приближенное решение u(m) задачи (1)–(6) с разрывным коэффициентом температуропроводности можно получить, если решать задачу, в которой в уравнении (1) этот коэффициент заменить на его гладкую аппроксимацию b(m). В качестве такой заме- ны можно, например, рассматривать его сглаживание в окрестности поверхностей разрыва с помощью интегрального усреднения с бесконечно дифференцируемым финитным ядром [11]:
b ( m ) ( x ) — J to p m ( I x — y I ) b ( y ) dy —
I
x
—
y
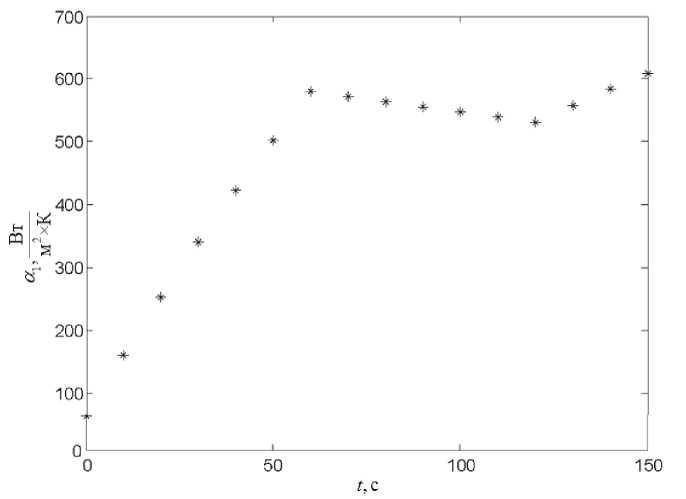
| m —4" J to f1x y 1 b(y)dy. Pm x—y mV P m' При этом to1(| £ |) — 0 при | £ |>1; J to1(| £ |) — 1. Предполагается, что p m ^ 0 при m ^ да . Функции b (m) имеют все производные любого порядка [6]. Поскольку b e Lq (G) (q > 0), то для любой подобласти G 'с G , отстоящей от границы G на расстоянии, не меньшем pm, усреднение b(m) сходится к b в Lq (G'), ) q ■ ^ 0 т. е. |b<-) —bq,G' q < sup J | b (x — v) — b (x) | dx Iv| m VG' при m ^ да . Таким образом, аппроксимации b(m) сходятся к b в норме пространства Lq (G). Известно также, что сходимость в Lq (G) влечет сходимость по мере, а из сходящейся последовательности функций по мере можно выбрать подпоследовательность, сходящуюся почти всюду [12]. Причем в [12] дан конструктивный метод построения такой подпоследовательности. В связи со сказанным далее будем считать, что такая подпоследовательность выбрана, и это есть последовательность b(m). В результате замены в (1)–(6) коэффициента температуропроводности функцией b(m) приходим к следующей краевой задаче: д u (m)=b (m) Л д2u (m)+ Д д b (m) д u (m) дt " (x)t; дxi +h дx дxz ’ u (m)(x ,0) — Ф( x), д u (m) дx1 — 0, x1——l1 д u (m) дx1 — 0, x1—l1 д u (m) дx 2 — 0, x 2——l2 д u (m) дx 2 — 0, x 2—l 2 , д u (m) λ дx3 — a1(t ) ( u—V1(t ) ) , x3 —0 , д u (m) —X---- дx3 — a2 (t)(u—V2(t)). Далее в работе будут использоваться следующие обозначения: дG - граница области G; xA — индикаторная функция множества A. Будем предполагать, что заданные в граничных условиях функции α1 , α2 , V1, V2 такие, что для некоторого 0 < а < 1 существует решение задачи (9)–(14) в пространстве Гельдера 3+а3+а H , 2 (QT) [10] (теорема 5.3, гл. IV). Доказано [13], что при выполнении условий существования и единственности решений задач (1)–(6) и (9)–(14) для любого е > 0 существует натуральное число mе такое, что при m > mе выполняется неравенство vraisup | и(m) - и |< е . Следовательно, выбирая радиус QT усреднения достаточно малым, можно с любой заданной точностью приблизить решение u(m) к u. Вероятностное представление решения. Для решений краевых задач для параболических уравнений известны вероятностные представления [14; 15]. Чтобы получить вероятностное представление решения задачи (9)–(14), введём систему СДУ: r Xr = x + J сvXG (Xv)dWT + T — t rr + J avXg (Xv)dv + J n(Xv )Xag (Xv)dKv, (15) T — t T—t Yr = 1 + J ai(v)Yvxx3(„)=o dKv + T — t r +J a2(v)YvXX3(v)=13dKv, (16) T — t r Zr = J a1(v)V1(v)YvXX3(v)=0dKv+ T — t r +J a2(v Wv)Yv XX3( v )=13dKv, (17) T — t r Kr = J XdG (Xv)dKv, (18) T — t где x e G - начальная точка для Xv; W.^ - трехмер- ный винеровский процесс; стv = (2b(m)(Xv))2; av -( 5b(m) ) вектор с координатами , i = 1, 2, 3; n(P) – ( dxi ) внутренняя нормаль в точке P e dG ; Kv - локальное время пребывания процесса Xv на границе, т. е. скалярный возрастающий процесс, который растет, только когда KvedG . Вероятностным представлением решения задачи (9)–(14) является математическое ожидание и (x, t) = Ex,T—t (ф(Xt )Yt + Zt ), (19) где символом Ex T—t обозначено математическое ожидание относительно вероятностной меры Px T—t, соответствующей случайному процессу, стартующему в момент времени T-t из точки x, т. е. XT—t = x. Приближенные значения u(m) (x,t) можно получить методом Монте-Карло путем статистического моделирования траекторий системы СДУ (15)–(18). Для этой цели в работах [6; 13] предлагалось использовать метод Эйлера. Моделирование траекторий методом Эйлера для СДУ (15)–(18) осуществляется по следующей схеме: Xi+1 = xi+ h2 0,4+ ha,(20) x+1 = X,A+1 +(A,+1 K)nxR3\G (XA1),(21) y,+1 = y, (1+ (a1)i Xag(xi)Ai+1K + + C«2)iX ag (x, )Ai+1 K),(22) z,+1 = z,+y,(a1),(V1), X ag(x)AI+1K + +У, (a2),(V2), X ag (x,)A,+1K, k+1 = k,+A,+1 K,(24) где , + 1 – номера узлов сетки; ξ – вектор трех независимых N(0,1) случайных величин; A,+1K = d (X A+1) -расстояние от XА1 до dG в случае выхода XА1 из области. Применение методов Эйлера и случайного блуждания по движущимся сферам. Поскольку в работе предполагается, что теплофизические свойства материалов, из которых состоит сотовая панель, являются постоянными величинами, то случайный процесс Xv в однородной среде, соответствующей каркасу или ячейке, с точностью до постоянного множителя совпадает с винеровским процессом. Известно, что точка первого выхода из шара винеровского процесса, начинающего движение из центра этого шара, имеет на границе этого шара равномерное распределение. При этом эта точка не зависит от времени первого выхода на границу. В связи со сказанным предлагается для ускорения моделирования траекторий СДУ (15)–(18) при их прохождении внутри ячейки использовать метод случайного блуждания по сферам, а движение по каркасу и некоторой его окрестности моделировать с помощью метода Эйлера с малым шагом. При решении нестационарных задач методом блуждания по сферам требуется каждый раз моделировать не только точку первого выхода из шара, но и время первого выхода. Для моделирования времени первого выхода из шара радиуса R в работе используется определение времени первого достижения уровня R бесселевским процессом, который является решением СДУ [8]: t St = S0 +J S— dr + Wt. Одномерный случайный процесс (19) получается в результате применения формулы Ито к евклидовой норме трехмерного винеровского процесса с начальной точкой x e G. При этом выполняется равенство S0 = Ilxll. Время первого выхода трехмерного винеровского процесса из шара радиуса R и время первого достижения случайным процессом уровня R имеют одинаковое распределение. Известны явные формулы для плотности времени первого достижения бесселевским процессом заданного уровня для начальных точек S0 = 0 и S0> 0 [9]. Но эти формулы представлены в виде рядов, содержащих функции Бесселя первого рода и их положительные нули, и поэтому численностатистическое моделирование по ним крайне затруднительно. С другой стороны, вместо заданного уровня, который требуется достичь, можно подобрать некоторые кривые, зависящие от t, такие, что получаются достаточно простые и удобные для моделирования формулы для плотности времени первого достижения бесселевским процессом этих кривых. Каждая такая кривая определяется задаваемой положительной сигмаконечной мерой μ . Определим функцию τ g ( a ) 3 e H , где H – гамма-распределенная случайная величина с параметрами 2 , 3 . В ходе вычислений, после того, 1 Л Г (t, x) =q (t, 0, x) — [ q (t, y, x )p( dy), a • a0 где q(t, y, x) – плотность вероятности перехода бессе-левского процесса; a – числовой параметр. Из свойства плотности q следует, что функции q и r удовлетворяют параболическому уравнению dv 1 52v 9 f 1 ) — =--т--1 — v I. dt 2 dx2dx V x ) Пусть функция g(t) такая, что на кривой x = g(t) выполняется равенство r(t,x) = 0. Тогда эту кривую можно рассматривать в качестве граничного условия к уравнению (27). Причем с учетом того, что бессе-левский процесс стартует из заданной точки, решение полученной краевой задачи определяется единственным образом. Обозначим τg время достижения бесселевским процессом этой подвижной границы, т. е. тg = = inf {t > 0, St = g(t)}. Можно показать [9], что плотность времени достижения границы x - g(t) = 0 удовлетворяет уравнению d f T „ p (t) =-— I r(t,x)dx g dt 1 V 0 Если положить ц(dy) = y2dy, то g(t) и pg (t) опре- деляются по формулам [9] f r g(t) = 2tln a Pg(t) = g3(t) 2at В этом случае получается простая формула для моделирования τg как получено значение τg , радиус сферы для определения очередной точки положения случайного процесса определяется по первой формуле в (29). Выбор параметра a дает возможность определить радиусы моделируемых шаров так, чтобы они не выходили за границы текущей ячейки и чтобы они не были слишком малы. В случае, если расстояние до границы ячейки менее некоторой заданной величины £, вычисления производятся согласно методу Эйлера. Результаты расчётов. Вычисления проводились для сотовой панели, каркас которой и ограничивающие пластины изготовлены из углепластика, а наполнителем служит воздух. Основные характеристики панели следующие: общая толщина панели – 0,035 м; толщина каждой из ограничивающих пластин панели – 0,001 м; толщина стенок сотового каркаса - 6 -10-5 м; сотовыми ячейками являются правильные шестиугольники одинакового размера с длиной стороны, равной 0,0042 м; коэффициенты температуропроводности углепластика и воздуха равны соответственно 8,0 -10-4 и 2,36 -10-5 м2/с. Граничные условия для расчётов были сформированы на основании физических характеристик, полученных по данным лётного эксперимента в холодном климате и соответствуют первым 150 с взлёта самолета. На рис. 1 приведён график коэффициента теплообмена на внешней стороне обшивки. На рис. 2 приведены полученные в результате расчётов при объёме выборки 2000 траекторий случайного процесса графики изменения значений температуры в середине панели и у края панели, обращённого внутрь салона. В табл. 1, 2 приведены для сравнения затраты времени счёта предложенным комбинированным методом и только методом Эйлера с различными шагами по каркасу hf и по объёму внутри ячеек ha . Результаты расчётов позволяют сделать следующие выводы: а) предложенный метод значительно эффективнее использовавшегося ранее метода Эйлера; б) так как при увеличении шага в методе Эйлера эффективность комбинированного метода растет по сравнению с методом Эйлера, то основная часть вычислительных затрат приходится на движение по тонкому каркасу; в) затраты в средней точке панели меньше, чем у края, поскольку в середине панели большая часть траектории приходится на движение по внутреннему пространству ячеек, где вычисления проводились с меньшим шагом. Рис. 1. Коэффициент теплообмена на внешней стороне обшивки Fig. 1. Heat transfer coefficient on the outside of the skin середина панели 235 L 0 ^с Рис. 2. Значения температуры внутри панели Fig. 2. Temperature values inside the panel Таблица 1 Затраты времени счёта в средней точке панели, с Метод ha = 2,5-10-7, hf = 2,5-10-8 ha = 5,0-10-7, hf = 5,0-10-8 ha = 10-6, hf = 10-7 Комбинированный метод 1064 548 154 Метод Эйлера 5839 3070 1563 Таблица 2 Затраты времени счёта вблизи границы x3 = 0, c Метод ha = 2,5 -10-7,hf = 2,5 -10-8 ha = 5,0.10-7, hf. = 5,0.10-8 ha = 10-6, hf = 10-7 Комбинированный метод 1394 479 188 Метод Эйлера 6193 4156 1854 Заключение. В работе предложен численно-статистический метод для оценки теплового состояния теплозащитных конструкций сотового типа. Данный метод основан на вероятностном представлении краевой задачи для параболического уравнения и комбинированном применении методов Эйлера и случайного блуждания по движущимся сферам. Получено значительное ускорение счёта по сравнению с моделированием траекторий только одним методом Эйлера. Acknowledgments. S. A. Gusev’s work was carried out with the financial support of the Russian Foundation for Basic Research, grant No. 17-01-00698 A.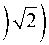
М
нижний край панели
Список литературы Численно-статистический метод для решения задач теплообмена в теплозащитных конструкциях сотового типа
- Результаты экспериментальной отработки спускаемой капсулы космического аппарата «Фобос-Грунт» для доставки образцов грунта Фобоса на Землю/С. Н. Алексашкин //Вестник ФГУП «НПО им. С. А. Лавочкина». 2011. № 5. C. 3-10.
- Николаев В. Н., Гусев С. А. Экспериментально-теоретические исследования негерметизированного отсека летательного аппарата с сотовыми конструкциями обшивки//Авиакосмическое приборостроение. 2017. № 9. C. 10-19.
- Николаев В. Н., Гусев С. А. Математическое моделирование теплового состояния отсеков и систем самолета с сотовыми конструкциями обшивки//Полёт: Общероссийский научно-технический журнал. 2017. № 5. С. 3-11.
- Nikolayev V., Gusev S. Heat condition compartments of aircraft with a honeycomb structure. Saarbrucken: LAMBERT Publ., 2017. 133 p.
- Николаев В. Н., Гусев С. А. Исследование теплового состояния отсеков пассажирского самолёта с сотовыми конструкциями фюзеляжа//Научный вестник Новосибирского государственного технического университета. 2016. № 1 (62). C. 146-167.
- Gusev S. A., Nikolaev V. N. Calculation of heat transfer in heterogeneous structures such as honeycomb by using numerical solution of stochastic differential equations//Advanced Materials Research. 2014. Vol. 1016. Р. 758-763.
- Muller M. E. Some continuous Monte Carlo methods for the Dirichlet problem//The Annals of Mathematical Statistics. 1956. Vol. 27, No. 3. Р. 569-589.
- Revuz D., Yor M. Continuous Martingales and Brownian Motion. 3 ed. Springer Publ., 1999. 602 c.
- Deaconu M., Herrmann S. Hitting time for the Bessel processes -walk on moving spheres algorithm (WOMS)//The Annals of Applied Probability. 2013. Vol. 23, No. 6. Р. 2259-2289.
- Ладыженская О. А., Солонников В. А., Ураль-цева Н. Н. Линейные и квазилинейные уравнения параболического типа. М.: Наука, 1967. 736 c.
- Соболев С. Л. Некоторые применения функционального анализа в математической физике. 3-е изд. М.: Наука, 1988. 336 p.
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. М.: Наука, 1976. 336 c.
- Гусев С. А. Применение СДУ к оценке решения уравнения теплопроводности с разрывными коэффициентами//Сиб. журн. вычисл. математики/РАН. Сиб. отд-ние. 2015. Т. 18, № 2. C. 147-161.
- Гихман И. И., Скороход А. В. Стохастические дифференциальные уравнения и их приложения. Киев: Наукова думка, 1982. 612 c.
- Кушнер Г. Дж. Вероятностные методы аппроксимации в стохастических задачах управления и теории эллиптических уравнений. М.: Наука, 1985. 222 с.


