Численное и экспериментальное исследование структуры течения в модели топки с псевдоожиженным слоем

Цитирование: Рогалев А. Н. Численное и экспериментальное исследование структуры течения в модели топки с псевдоожиженным слоем / А. Н. Рогалев, И. И. Феоктистов, П. А. Брызгунов, А. Н. Вегера, Писарев Д. С. // Журн. Сиб. федер. ун-та. Техника и технологии, 2025, 18(8). С. 1002–1012. EDN: KHZQWV

Одним из перспективных подходов к решению задачи снижения объема выбросов является внедрение высокоэффективных и экологичных технологий газификации и сжигания, таких как использование установок с псевдоожиженным слоем. Газификация и сжигание топлива в псевдоожиженном слое обеспечивает интенсивный массо- и теплообмен между частицами топлива и окислителем, что практически исключает механический и химический недожог. Это делает целесообразным применение таких установок для применения низкореакционных видов топлива.

Несмотря на потенциал широкого применения технологий газификации и сжигания в псевдоожиженном слое и их значимость для развития энергетики, в отечественной промышленности они пока не получили массового распространения. Одной из причин этого является сложность проектирования установок псевдоожиженного слоя, связанная с необходимостью учета динамики движения частиц в слое, включая процессы их уноса, сепарации и рециркуляции в топку.

Для инженерных расчетов установок с псевдоожиженным слоем рационально применение численного моделирования с целью предварительной оценки работоспособности разработанной конструкции топки. Однако ввиду сложности математических моделей описания движения частиц слоя необходима валидация результатов моделирования посредством сопоставления с экспериментальными данными с целью определения применимости выбранных моделей и методов.

Для моделирования запыленных потоков применяются два подхода [2, 3] к численному моделированию многофазного потока: метод Эйлера-Лагранжа [4, 5] и метод Эйлера-Эйлера [6, 7]. Эти модели отличаются друг от друга методом описания рабочих сред и их взаимодействия друг с другом, что оказывает существенное влияние на точность результатов моделирования и скорость проведения расчета.

В модели Эйлера-Лагранжа первичная фаза рассматривается как континуум путем решения усредненных по времени уравнений Навье-Стокса [8, 9]. Поведение дисперсных фаз определяется путем отслеживания большого количества частиц с помощью рассчитанного поля потока первичной фазы. В ходе расчетов течения первичной фазы рассчитываются траектории частиц в заданных интервалах, при этом дисперсные и первичные фазы могут обмениваться массой, импульсом и энергией. Основное предположение в этой модели состоит в том, что объемная доля дисперсной вторичной фазы составляет менее 10–12 %, хотя ее масса может быть больше массы первичной фазы [10].

Различные фазы в подходе Эйлера-Эйлера рассматриваются как взаимопроникающие континуумы, представляя таким образом фазовые объемные доли как непрерывные функции времени и пространства [11]. Сумма всех объемных долей фаз в каждой расчетной ячейке равна единице. К каждой фазе применяются законы сохранения, чтобы получить систему уравнений, аналогичную для всех фаз. Поскольку в этой модели дополнительные уравнения сохранения массы и импульса решаются для каждой фазы отдельно, существует возможность смоделировать любую комбинацию жидкой, газовой и твердой фаз [12, 13].

В табл. 1 представлено обобщенное описание моделей, используемых для моделирования течения плотного газа и твердого тела в контексте псевдоожижения газа.

Метод Эйлера-Лагранжа является более точным, так как просчитывает движение частиц и может учитывать их взаимодействие друг с другом и поверхностью стенок камеры, но такой расчет требует привлечения существенных вычислительных мощностей и занимает продолжительное время, при это решаться такая задача может только в потоке.

Таблица 1. Классификация различных моделей псевдоожижения [14, 15]

Table 1. Classification of different fluidization models [14, 15]

Модель	Уравнение твердой фазы	Уравнение жидкой фазы	Область применения
Дискретная пузырьковая модель	Лагранж	Эйлер	Промышленные установки (<10 м)
Двухжидкостная модель	Эйлер	Эйлер	Инженерные расчеты (1м)
Неразрешенное уравнение дискретных частиц	Эйлер	Лагранж	Лабораторные исследования (0,1 м)
Разрешенное уравнение дискретных частиц	Эйлер	Лагранж	Лабораторные исследования (0,01 м)
Молекулярная динамика	Лагранж	Лагранж	Лабораторные исследования (<0,001 м)

При этом метод Эйлера-Эйлера менее точный, так как не рассматривает каждую отдельную частицу, но позволяет относительно быстро оценить влияние отдельных геометрических параметров геометрии камер и гидродинамических характеристик потока на процесс псевдоожижения слоя. Однако по причине низкой точности метода результаты моделирования должны быть валидированы путем постановки эксперимента.

Данная работа посвящена численному и экспериментальному исследованию структуры течения в псевдоожиженном слое в модельных камерах с кипящим и циркулирующим кипящим слоем с целью определения применимости упрощенного эйлеровского подхода к моделированию задач такого класса.

Объект и методы исследования

Явление псевдоожижения наблюдается при подаче через слой частиц ожижающего агента со скоростью, достаточной для начала движения частиц, также называемой критической скоростью. При этом скорости потока недостаточно для витания частиц, из-за чего вынесенные из слоя частицы падают обратно в слой. По этой причине для агрегатов с кипящим слоем (КС) характеризующей является критическая скорость, поскольку необходимо добиться явления псевдоожижения и минимизировать унос частиц из слоя. В то же время для агрегатов с циркулирующим кипящим слоем (ЦКС) за счет организации возврата унесенных и уловленных частиц обратно в топочное пространство характеризующей является скорость витания.

Из-за разных характеризующих скоростей для КС и ЦКС были разработаны две различные камеры. Целью экспериментального исследования является изучение распределения концентраций частиц во внутреннем пространстве камер с различной геометрией в зависимости от скорости ожижающего воздуха. Скорость ожижающего воздуха определялась при помощи дифманометра на входе в установку. В табл. 2 приведены параметры, при которых проводилось экспериментальное исследование.

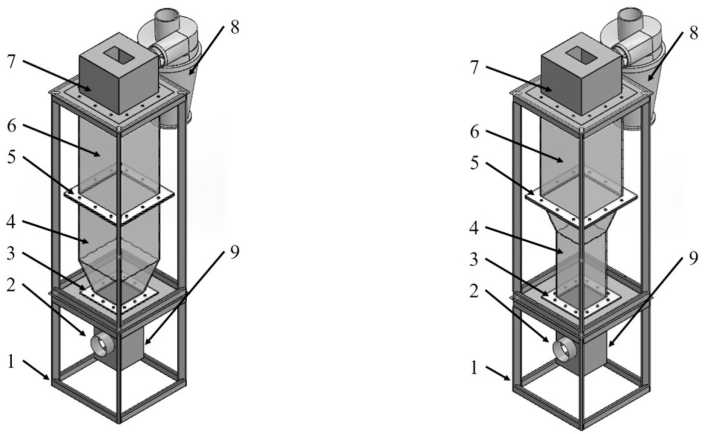
На рис. 1 а и б представлена трехмерная модель КС и ЦКС. Особенностью данного стенда является сменяемый прозрачный короб, который позволяет визуально фиксировать потоки движущихся частиц под воздействием потока воздух.

Таблица 2. Условия проведения эксперимента

Table 2. Experimental conditions

Величина	Значение
Атмосферное давление, мм рт. ст.	Р возд = 762
Температура, °C	Т возд = 27
Молярная масса, кг/моль	М = 0,029
Универсальная газовая постоянная, Дж/моль К	R = 8,34417

б) стенд с камерой КС b) stand with a BFB camera

a) стенд с камерой ЦКС a) stand with a CFB camera

Рис. 1. Лабораторный стенд для исследования гидродинамики псевдоожиженного слоя: 1 – каркас; 2 – воздухораспределительная камера; 3 – малый фланец; 4 – сменная камера; 5 – большой фланец; 6 – основная камера; 7 – крышка; 8 – циклонный сепаратор; 9 – место подключения дифманометра

Fig. 1. Laboratory bench for studying the hydrodynamics of a fluidized bed: 1 – frame; 2 – air distribution chamber; 3 – small flange; 4 – replaceable chamber; 5 – large flange; 6 – main chamber; 7 – cover; 8 – cyclone separator; 9 – connection point of the diffmanometer

Рабочий материал с размером частиц не менее диаметра ячейки воздухораспределительной решетки равной 1 мм загружается через верхнее отверстие в крышке 7. Воздух поступает через трубопровод диаметром 102 мм в воздухораспределительную камеру 2 и проходит через решетку квадратного сечения 150 х 150 мм. Далее запыленный поток воздуха попадает в циклонный сепаратор 8 в котором происходит улавливание унесенных частиц слоя, а очищенный воздух уходит обратно в атмосферу.

Чтобы стенд не получил повреждений, поток воздуха изначально запускается в трубопровод, подключенный параллельно. Далее при помощи задвижки поток воздуха перенаправляют в соединительную трубу, подключенную к стенду. Одновременно с этим производились замеры избыточного давления воздуха при помощи дифманометра Trotec TA400 с трубкой Пито-Прандтля.

Перед проведением эксперимента был проведен предварительный расчет по определению скоростей псевдоожижения для гречневой крупы, используемой в качестве модельного мате-– 1006 – риала. В табл. 3 приведены результаты этого расчета, которые впоследствии использовались для задания граничных условий при численном моделировании, а на рис. 2 показаны геометрические размеры модели и соответствующая сетка для камеры ЦКС.

Таблица 3. Исходные данные для численного моделирования

Table 3. Initial data for numerical modeling

Величина	Значение
Эквивалентный диаметр частиц, мм	d ч = 3,2
Истинная плотность частиц, кг/м3	ρ ч = 1060
Плотность воздуха, кг/м3	ρ в = 1,205
Кинематическая вязкость воздуха, м2/с	ϑ в = 15,11 ∙ 10–5
Скорость начала ожижения, м/с	W кр = 0,302
Скорость витания, м/с	W вит = 6,917

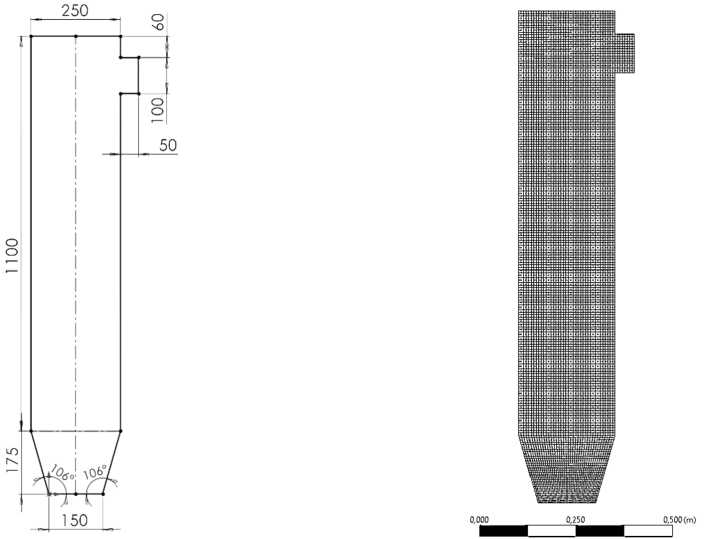
Рис. 2. Геометрические размеры и расчетная сетка для моделирования камеры ЦКС

Fig. 2. Geometric dimensions and computational grid for modeling the CFB chamber

Расчет проводился для режимов псевдоожижения со скоростями подачи воздуха 1,5; 4; 5 и 6 м/с. Расчет пристеночной функции осуществлялся методом Scalable Wall Function модели турбулентности k- ε. Выбор этой функции был обусловлен обеспечением стабильности расчета при моделировании псевдоожиженного слоя в нестационарной постановке в течение относительно длительных промежутков времени (25 с). Размер ячейки расчетной сетки был принят равным двум диаметрам частицы (6,4 мм).

В псевдоожиженном слое от распределения потока частиц зависят скорости реакций и поведение теплопередачи. Поэтому необходимо оценить этот поток частиц, чтобы лучше понять распределение частиц и массовую нагрузку в топке. Поток частиц состоит из двух компонентов: восходящего потока и нисходящего потока. Восходящий поток располагается в центре поперечного сечения топки из-за высокого сопротивления движению газа материалом, при этом нисходящий поток частиц возникает в пристеночном пространстве. Движение этих потоков характеризуется высоким содержанием частиц слоя, что позволяет их визуально наблюдать.

В качестве модельного материала использовалась крупа гречневая. Движение частиц материала и распределение их концентраций исследовались посредством видеофиксации.

Результаты исследования

Данные, полученные в результате проведения опытов, занесены в табл. 4 и 5.

На рис. 3 и 4 представлены распределения концентраций внутри рабочих камер для ЦКС и КС при различных скоростях подачи ожижающего агента соответственно. Как видно, частицы преимущественно витают в центральной части потока, а в пристеночном пространстве камеры падают обратно в слой.

Таблица 4. Результаты испытаний камеры ЦКС

Table 4. Results of the CFB chamber tests

Номер испытания	Измеренное давление Р изб , Па	Скорость воздуха в сечении трубопровода V возд.труб , м/с	Действительный расход воздуха G возд , кг/с	Скорость воздуха в сечении воздухораспределительной решетки V возд.реш , м/с
1	74	11,07	0,106	4,023
2	110	14,00	0,134	5,084
3	168	16,77	0,161	6,090

Таблица 5. Результаты испытаний камеры КС

Table 5. Results of the BFB chamber tests

Номер испытания	Измеренное давление Р изб , Па	Скорость воздуха в сечении трубопровода V возд.труб , м/с	Действительный расход воздуха G возд , кг/с	Скорость воздуха в сечении воздухораспределительной решетки V возд.реш , м/с
1	70	11,53	0,111	4,187
2	115	13,63	0,131	4,950
3	165	17,71	0,170	6,431

В камере ЦКС при низких скоростях наблюдалось явное разделение концентраций частиц на зоны с максимальной концентрацией частиц, разбавленной фазы и уровня максимального подъема частиц по высоте камеры, причем при скорости 6 м/с разбавленная фаза занимала целиком весь объем камеры. В камере КС при аналогичных условиях такого явления не наблюдается, поскольку из-за специальной геометрии в слое создается больший перепад давления и частицы, выброшенные из верхней части, быстрее возвращаются обратно (рис. 4).

2) 4 м/с

2) 4 m/s

4) 6 м/с

4) 6 m/s

1) 1,5 м/с

1) 1.5 m/s

3) 5 м/с

3) 5 m/s

ЛГУ

Рис. 3. Распределение частиц в камере ЦКС при различных режимах

Fig. 3. Particle distribution in the CFB chamber under various modes

Fig. 4. Particle distribution in the BFB chamber under various modes

В результате численного моделирования псевдоожижения слоя по рассмотренной ранее методике были получены эпюры распределения концентраций частиц во внутреннем объеме топочной камеры, представленные на рис. 5.

На основании полученных данных экспериментального исследования была проведена оценка погрешности результатов численного моделирования для камер КС и ЦКС при скорости подачи воздуха 4, 5 и 6 м/с (рис. 6). Установлено, что отклонение измеренных величин не превышает 5 %, что позволяет сделать вывод о том, что результаты численного моделирования качественно соотносятся с данными эксперимента.

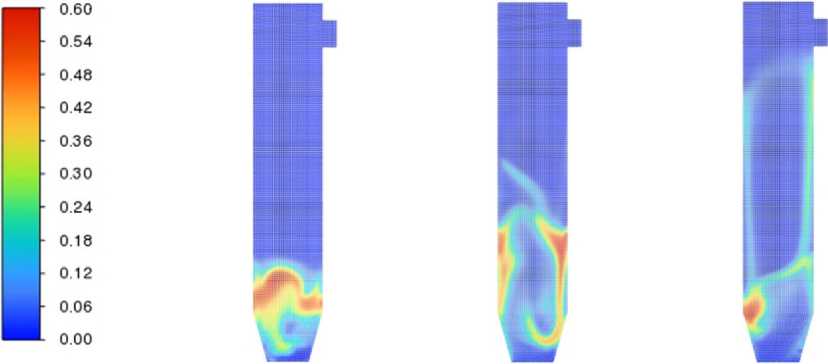
Объемная доля (твердая)   1) 1,5 м/с              2) 4 м/с                3) 5 м/с

Volume fraction (solid)       1) 1.5 m/s              2) 4 m/s                 3) 5 m/s

Рис. 5. Результаты численного моделирования

4) 6 м/с

4) 6 m/s

Fig. 5. Numerical simulation results

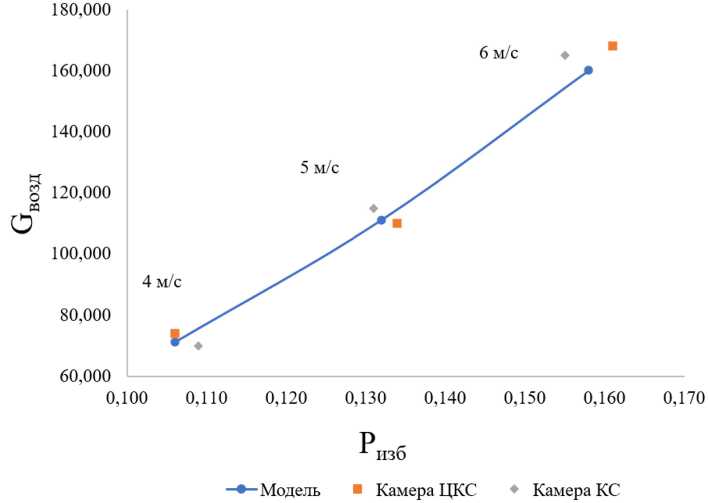
Рис. 6. Зависимость давления от расхода воздуха

Fig. 6. Dependence of the pressure on the air flow

Заключение

• 1.    Разработан экспериментальный стенд для исследования структуры течения в топках с псевдоожиженным слоем. Его особенность заключается в возможности визуального наблюдения потоков через прозрачные стенки, а также возможность моделирования течений в камерах КС и ЦКС.

• 2.    Основываясь на полученных данных, можно сделать вывод, что моделирование псевдоожиженного слоя в постановке модели Эйлера-Эйлера не требует построения особенно мелких и точных расчетных сеток, поскольку сама по себе постановка задачи численного моделирования режима псевдоожижения слоя частиц накладывает ряд ограничений и допущений. При этом гораздо более важную роль играет возможность проведения численного моделирования в нестационарном режиме достаточно длительного временного отрезка при сравнительно низких требованиях к вычислительным мощностям. Такой подход обеспечит решение различ-

• ных инженерных и конструкторских задач, которые лежат в основе разработки и совершенствования рабочих камер агрегатов КС и ЦКС.

• 3.    По результатам экспериментальных исследований определены концентрации распределения частиц слоя по внутреннему объему в двух характерных рабочих камерах для агрегатов КС и ЦКС. Установлено, что в камере ЦКС при скорости 1,5 м/с происходит разделение потока частиц на зоны с максимальной концентрацией частиц в нижней части камеры, разбавленной фазы в центральной части и уровня максимального подъема частиц по высоте камеры, в то же время при скорости 6 м/с разбавленная фаза занимала целиком весь объем камеры. В камере КС при аналогичных условиях разделения потока не было зафиксировано, поскольку из-за сужения в нижней части камеры в слое создается больший перепад давления и частицы, выброшенные из верхней части, быстрее возвращаются обратно.

• 4.    Было проведено численное моделирование процесса псевдоожижения с использованием континуальной модели Эйлера-Эйлера. Было установлено, что расхождение результатов моделирования с данными экспериментального исследования по перепаду давления в слое частиц составляет не более 5 %.

• 5.    На основании результатов проведенного численного и экспериментального исследования установлено, что численное моделирование процесса псевдоожижения воспроизводит структуру течения потока в топках с КС и ЦКС достаточно точно для качественных оценок эффективности инженерных и конструкторских решений, направленных на разработку и внедрение технологии газификации и сжигания в псевдоожиженном слое в отечественной энергетике.