Численное и экспериментальное исследование термоакустического охладителя на пульсационной трубе

течения и переходн ых процессов в различных компонентах конструкции пульсационного охладителя. В работе [6] представлены результаты применения комбинированного 1-D моделирования в узловых точках и 2-Dмоделирования контрольны х объем ов в теплообменниках, регенераторе и пульсационной трубе для исследования термодинамических про цессов и опти мизации конструкции охладителя. Сравнительно недавно были предприняты попытки моделирования процессов в пульсационных охладителях в готовых программных продуктах, в том числе с учетом нестационарности процессов теплообмена. В работе [7] представлены результаты численного моделирования во Fluent, демонстрирующие возмущения потока, характерные для малых величин отношения диаметра к длине элементов конструкции, которые отрицательно сказываются на производительности охладит еля вследствие перемешивания потоков. Результаты расчета с помощью тепловой неравновесной модели для исследования процессов в пористых средах (теплообменники и регенератор) и учет толщины стенок элементов конструкции пульсационного охладителя с инерционной трубой представлены в [8]. Пример CFD модели, где одновременно решаются уравнения неразрывности, количества движения и энергии для газа (гелия) и для пористой стенки (теплообменников, регенератора) приведено в [9].

Целью данной работы является использование 1-D моделирования и CFD-моделирования для проработки этапов инженерного расчета конструкции установки пульсационного охладителя криогенного уровня температур.

Комплексный подход в получении параметров геометрии конструкции и рабочего процесса криогенного пульсационного охладителя (КПО) заключался в использ овании аналитического и численного моделирования рабочего процесса с помощью термодинамики, волновой теории и САЕ-систем. В качестве предпроектной оцен- ки геометрии конструкции с целью получения минимального уровня охлаждения

Т_хол исполь -

зуется модифицированная методика расчета криогенного пульсационного охладителя [10]. Ав- торами введены поправки в методику, связанные с изменением конструктивной схемы, в которую были добавлены теплообменники охлажде ния, ресивер и инерционная труб ка (рис. 1).

Особенностью данной методики является нахождение параметров на каждом этапе рабочего цикла с учетом различных схем перетекания масс рабочего тела в элементах конструкции пульсационного охладителя. Теоретическая модель идеализированного рабочего цикла описывается процессами наполнения объема охладителя, проталкивания рабочего тела в процессе сжатия, его изоэнтропное расширение в пульсационной трубе с отводом тепла в холодильнике и необратимое адиабатное сжатие газа в ресивере, необратимое адиабатное и изоэнтропное расширение газа при обратном ходе поршня. Расчет производился с допущ ением идеального теплообмена в холодильнике, регенераторе и теплообменнике, процессы в пульсационной зоне и ресивере адиабатные, гидравлические сопротивления по длине охладителя не учитывались, принималось ступенчатое проведение процессов с мгновенным изменением параметров в полостях. Несмотря на дискретность рассматриваемых процессов рабочего цикл а охладителя аналитическая методика, тем не менее, поз воляет учесть различные варианты получения полезной нагрузки с учетом различной геометрии конструкции, давления заправки, степени повышения давл ения в пульсационной трубе и др.

Для каждого элемента конструкции охладителя записывались уравнение сохранения энергии как для открытой термодинамической системы и уравнение состояния :

dM _ dp dV dT dz

М p V T z, а также полученное в [10] уравнение изменения параметров с учетом изменения температуры рабочего тела dp p

dV dT

(1 — 1 )--1 ---- a V aT

T k

—

T a

где Т_а – переменная температура рабочего тела, k _ c_p / c_v - показатель адиабаты, z - безразмерный коэффициент сжимаемости z = pv / RT .

Для расчета была взята конструктивна схема, представленная на рис. 1 с размерами (табл. 1), приведенными в работе [2] для возможности сравнения результатов с экспериментальными данными, приведенными в данной работе.

Рассматривались три различных варианта распределения рабочего тела (гелий) в рабочей зоне,

Таблица 1. Геометрические параметры и материал ы элементов установки

Элемент	Радиус, м	Длина, м	Материал
Компрессор	0,03	0,011	-
Передающая труба	0,0085	0,04	Нержавеющая сталь
Предохладитель	0,0085	0,03	Медь
Регенератор	0,0085	0,06	Нержавеющая сталь
Теплообменник нагрузки	0,0047	0,05	Нержавеющая сталь
Пульсационная труба	0,0047	0,23	Нержавеющая сталь
Холодильник горячий	0,0047	0,03	Медь
Дроссель	-	-	Латунь
Инерционная труба	0,00193	1,5	Медь
Ресивер	0,026	0,149	Нержавеющая сталь

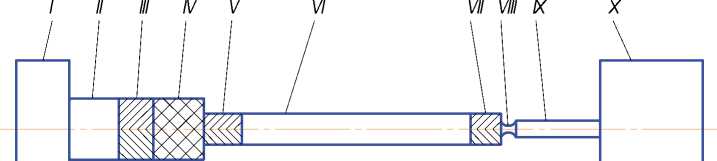
Рис. 1. Схема криогенного охладителя на пульсационной труб е:

I – компрессор; II – проходная труба; III – вторичный холодильник; IV – регенератор; V –теплообменник нагрузки; VI – пульсационная труба; VII – холодильник; VIII – дроссель; IX - инерционная труба; X – ресивер начиная с процесса сжатия и процесса внутреннего адиабатного расширения (здесь примем, что в начале цикла в установке имеется масса остаточного газа М1, часть газа М2 и М3 поступают в рабочую зону в процессах наполнения и проталкивания):

• 1    режим. Во время процесса проталкивания и внутреннего адиабатного расширения при открытом дросселе только часть остаточной массы М 1 уходит в ресивер, в пульсационной трубе остается М 1’ и М1р соответственно.

• 2    режим. Во время процесса проталкивания весь остаточный газ М1 уходит в ресивер (М1’=0), а затем, при внутреннем адиабатном расш ире-нии часть массы М2 утекает в ресивер, в трубе остается М2р.

• 3    режим. Во время внутреннего адиабатного расширения весь остаточный газ перетекает в ресивер (М1р=0).

Расчет производился для трех параметров давления заправки 1.4, 1.74, 2.2 МПа, значения давления в ресивере для расчета были получены с помощью численного моделирования конструкции в ESIACE+ CFD (табл. 2).

Сравнение полученных уровней температуры охлаждения производилось с данными работы [10], в которой прив едены экспериментальные данные для конструкц ии с таким же соотношением объемов пульсационной трубы и ресивера при аналогичных рабочих режимах (давление заправки, рабочая частота). Результаты сравнения демонстрируют отклонения от экспериментальных значений 5-10% (табл. 3).

На рис. 2 приведено изменение средней температуры в пульсационной трубе на трех расчетных режимах при разном среднем давлении в установке. Из графика видно, что рабочее тело

Таблица 2. Варианты для расчета модели охладителя

№ варианта	Давление заправки Рср, МПа	Давление в ресивере р 1 PV МПа	Ход поршня X, м	Рабочая частота f, гц	Амплитуда давления АР, МПа
1	1,41	1,375	0,00210	65	0.2
2	1,74	1,715	0,00195	65	0.2
3	2,2	2,167	0,00175	65	0.2

Таблица 3. Сравнение расчетных значений температуры теплообменника нагрузки с экспериментальными значениями [10]

№ режима	Давление заправки, Р , МПа	Тжс ’ К	т^.к	Р,%
1	1,41	142	159,4	9,6
2	1,74	129	141,5	8,8
3	2,2	126,5	123,2	2,6

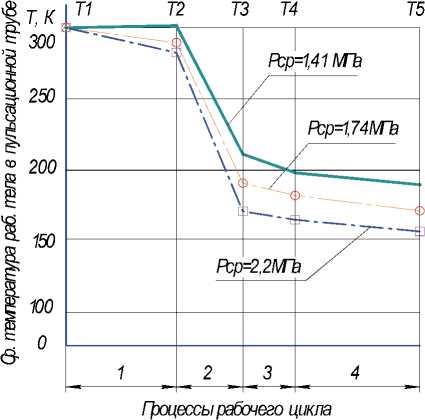
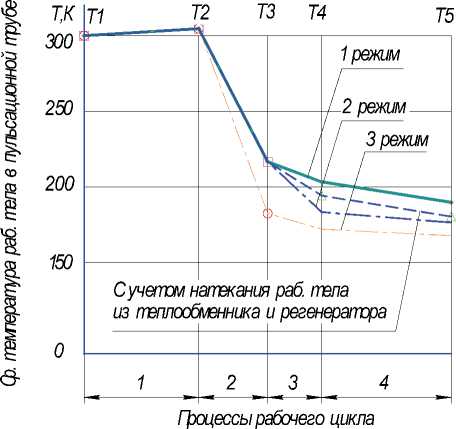
Рис. 2. Изменение средней температуры в пульсационной трубе для Рср=1,41МПа; 1,74МПа и 2,2МПа

Рис. 3. Изменение средней температуры рабочего при разном распределении рабочего тела по элементам установки для Рср=1,41МПа имеет наименьшую температуру охлаждения Т5=156,9 К (температура рабочего тела во время выталкивания) при наибол ьшем среднем давлении 2,2 МПа. Это соответствует тому, что одним из способов достижения наименьш ей температуры охлаждения, а значит, наибольшей эффективности является повышение давление в контуре охладителя.

На рис. 2 показано изменения среднего давления в пульсационной трубе при разном распределении рабочего тела по элементам установки при Рср=1,41МПа, Рр1=1,375МПа. Хор ошо видно, что наибольшего охлажден ия рабочее тело достигает при полном перетекании остаточного газа в ресивер по время внутреннего адиабатного расширения (при М1р=0, Т5=176,4 К) и проталкивания (при М1’=0, Т5=179,4К). Это соответствует выводам о том, что данный режим соответствует наибольшей эффективности и минимальному уровню охлаждения, указанных в [10].

С использованием зависимостей минимал ь-ного температурного уров ня охлаждения в те-плообм еннике нагрузки от соотношения объема пульсационной трубы и объёма ресивера, полученных с помощью предпроектной методики, была разработана модель расчета конструктив- ных параметров термоакустического охладителя.

Для разработки расчетной модели был использован программный комплекс DeltaEC (Design Environment for Low-amplitude ThermoAcoustic Energy Conversion – разработка Los Alamos National Laboratory, USA, версия - 6.3b11(Win,18-Feb-12), свободная лицензия), предназначенный для моделирования акустических устройств и описания термоакустических процессов в них и являю щийся основным средством получения их конструктивных параметров. DeltaEC вы- полняет численное интегрирование в одном измерении, используя низкоамплитудную линейную аппроксимацию уравнений Ротта для решения одномерных волновых уравнений последовательности сегментов ко н струкц и и и гармоническую временную зависимость изменения рабочих параметров. Рабочий контур термоакустического охладителя разбивался по длине на сегменты, соответствующие основным конструктивным элементам пульсационного охладителя . Комплексные величины давления и объемной скорости рассчитываются от сегмента к сегменту c учетом граничных условий и заданных параметров “целей” и “предположений” для выполнения численного интегрирования основных уравнен ий линейной термоакустики. Значения параметров основных конструктивных размеров приведены в табл. 4.

Комплексность подхода при исследовании рабочего процесса в контуре термоакустического охладителя включала в себя также моделирование газодинамических течений в термоакустическом охладителе в двух программных продуктах ESICFDACE+ и ANSYS Fluent. Для модел ирования термоакустического охладителя была построена его двум ерная модель по полученным размерам, наложена структурированная конечно-элементная сетка (106406 ячеек). Так как конструкция охладителя осесимметрична, то для моделирования была построена только половина его модели.

Исходные параметры модели на входе приведены в табл. 5. Затем были проведены настройки граничных условий в соответствии с табл. 6.

Для имитации возвратно-поступательного движения поршня компрессора в GUI интерфейсе задавалась скорость движения стенки порш ня в цилиндре (компонент “ I ” на рис. 1). Закон изме-

Таблица 4. Размеры основных конструктивных элементов, полученных с помощью Delta EC

Элемент конструкции	Радиус, м	Длина, м	Толщина стенки, м
Поршень компрессора	3-10"2	2,ТПУ2	-
Передающая труба	8,5-10"3	4-102	8-10"3
Входной теплообменник	8,5-КУ3	3-1 (У2	1,07-Ю3
Регенератор	8,5-ПУ3	6-10"2	1,07-Ю3
Холодный теплообменник	5,7-Ю-3	5-ПУ2	1,65-Ю’3
Пульсационная труба	5,7-Ю-3	2,2-Ю1	1,65-Ю3
Горячий теплообменник	5,7-Ю-3	4-10’2	1,65-Ю3
Инерционная труба	1,93-Ю"3	1,2	1,25-Ю’3
Ресивер	2,6-10"2	1,49-1О1	5-1(У3

Таблица 5. Исходные параметры модели на входе

Величина	Значение
Среднее давление газа, МПа	1,41; 1,74; 2,2; 3,1
Частота, Гц	55; 65;75
Температура газа, К	293
Ход поршня, мм	2,1; 1,95; 1,75; 1,5

Таблица 6. Гр аничные усл овия

Элемент Граничные условия Пористость Материал Компрессор adiabatic - Сталь Передающая труба я=20Вт/м2К - Сталь Входной теплообменник Т=293°К 0,774 Медь Регенератор adiabatic 0,72 Сталь Холодный теплообменник adiabatic 0,774 Медь Пульсационная труба adiabatic - Сталь Горячий теплообменник Т=293°К 0,774 Медь Инерционная труба adiabatic - Медь Ресивер adiabatic - Сталь нения скорости w движения поршня описывается выражением w=2πf·A0cos(2πf·t), где A0 – ход поршня, f– частота. Для перестройки сетки используется схема бесконечной интерполяции [10].

Производилось моделирование рабочего процесса в течение 10 секунд работы каждой модели термоакустического охладителя. Время счёта составил о около 72 часа, значения температуры на холодном теплообменнике фиксировались каждую с шагом 0,1 секунды.

Время работы каждой расчётной модели термоакустического охладителя – 10 секунд. Время счёта составляет около 72 часа на каждую модель. Значения температуры на холодном теплообменнике фиксировались через 0,1 с.

Отдельным этапом подготовки расчета являлась настройка характеристик в пористых элементах (теплообменниках и регенераторе). Теплообменники выпол нены из медного сплава, обладаю щего следую щими физическими характеристиками: коэффициент теплопроводности 392 Вт/мК, теплоемкость 380 Дж/кгК, плотность 8950 кг/м3.

Регенератор вы полнен из нержавею щей стали. Теплофизические характеристики материала регенератора: коэффициент теплопроводности 22 Вт/мК, теплоемкость 460 Дж/кгК, плотность 7810 кг/м3. В соответствующих опциях для пористых структур вводятся основные параметр ы, представленные в табл. 7.

Тепловой поток в пористой среде, возникающий за счет теплопроводности, излучения и процесса диффузии определяется следующим выражением:

Ng

q = AV T + qR I ^ Jh, i=1

где Ng– количество газовых фаз в системе, hi – их энтальпия, соответственно, и J – потоки диффузии. T – температура пористого материал а и qR - тепловой поток за счет излучения. X - приведенная теплопроводность пористой среды определяется по формуле:

X = — 2^ s +1—

51 -г

2Х s + Xf3Х где Xs - теплопроводность материала среды, Xf – теплопроводность потока газа в порах, – пористость среды.

Численная схема для решения основных уравнений основан на методе конечных объемов. Ур авнения неразрывности, импульса и энергии решаются для жидкости, а также пористых сред с помощ ью метода «Upwind» 2-го порядка.

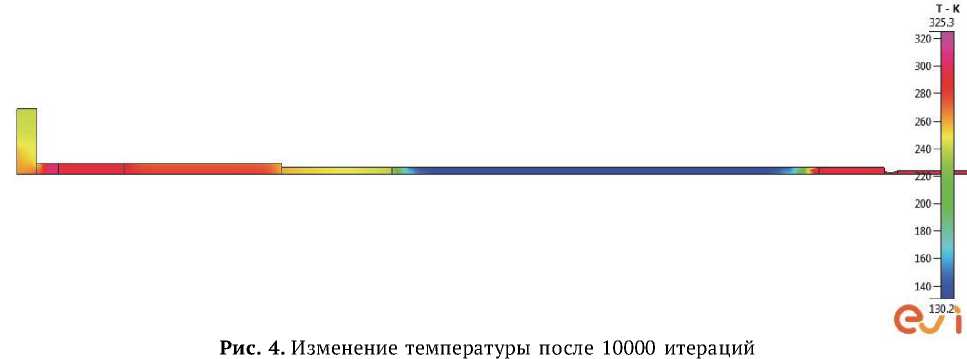
Для расчета производных по времени в уравнениях непреры вности, импульса и энергии используется схема Crank-Nicholson 2-го порядка (с коэфф ициентом смешивания 0,7) [11]. Шаг по времени в расчетах составлял (1,2·10-4 с), состоящий из 80 шагов за цикл и обеспечивал достаточно высокую точность расчета. Общий критерий сходимости для всех переменных был установлен равным 10-4 для решателя схемы «Implicit».Также в ходе расчета проверяется выполнение законов сохранения массы и энергии. Изменение температуры по длине пульсационного охладителя после 10000 итераций представлено на рис. 4.

Для моделирования процессов в охладителе с помощью программы Ansys Fluent была построена аналогичная двухмерная модель по размерам, представленным в табл. 1 и проведены соответствую щи е настройки граничных условий. Для имитации колебаний пор шня компрессора была использована модел ь с динамичной сеткой. Для

Таблица 7. Основные характеристики пор истых элементов

Элемент	Объемная пористость	Проницаемость, м2	Коэффициент сопротивления
Теплообменные аппараты	0,774	4,08 -Ю"8	0,2
Регенератор	0,72	9,7-Ю-11	0,3

задания движения поршня в Ansys Fluent была использована опция «In-Cylinder», позволяющ ая задать необходимый закон движение поршня. При использовании данной опции шаг расчёта был задан в зависимости от угла поворота коленчатого вала и составил 3 градуса. В зависимости от частоты шаг изменялся от 0,11мс до 0,15мс. Время сч ёта каждой расчётной модел и составило около 60 часов c использованием персонального компьютера на базе процессора Intel CoreI 7-4770K 3.5 GHz, 32 GB, SSD 240GB.

Для расчёта коэффициента теплопроводности в пористой ср еде используется формула:

X = eX f +(1 -e^X s,

При частоте колебаний 55 Гц за время расчёта более низкая температура охл аждения была получена с помощью ESI в среднем на 10K (табл . 8), а при 75 Гц большую степень охлаждения показал

Fluent. При частоте 65 Гц степень охлаждения практически одинаковая. Основываясь на данных результатах моделирования, был спроектирован пульсационный охладитель для дальнейшего изучения факторов, влияю щих на его работу.

На рис. 5 показано изменение температуры газа на холодном теплообменнике. Как видно из рисунка при численном моделировании с по-мощ ью ESI скорость охлаждения выше, чем при использовании программы ANSYS Fluent. Это связа но с различным математическим описанием блока расчета процессов тепло-массопереноса в двух различных программных пр одуктах.

Для получения фактических характеристик холодильника, подтверждения теоретических данных и расчётных методик был разработан и спроектирован экспериментальный образец криогенного холодильника (рис. 6). В процессе эксперимента холодильник заправляется гелием

Таблица 8. Температура газа на холодном теплообменнике за 10 с работы

№ режима/частота	1/55	1/55	1/55	2/65	2/65	2/65	3/75	3/75	3/75
ESI	155	155	152	152	151	150	150	150	142
Fluent	167	148	137	174	144	136	164	153	128

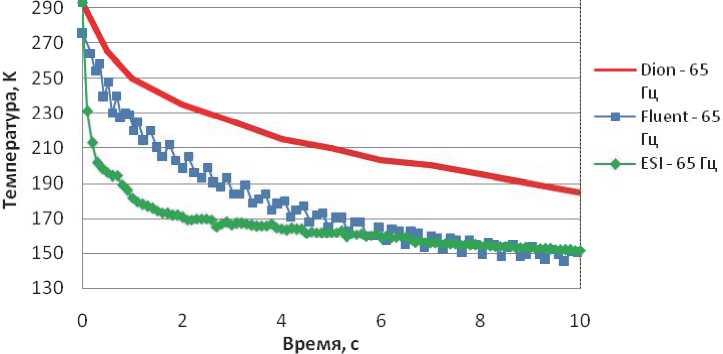
Рис. 5. И зменение температуры газа на холодном теплооб меннике для режима Рср=2,2МПа и ходе поршня 1,75мм

Рис. 6. Внеш ний вид экспериментал ьной установки

при температуре 300 К при различных давлениях (0,5…3,5МПа).

Криогенный пульсационный охладитель содержит (в соответствии с рис. 7): линейный генератор (альтернатор) (1); предохладитель (2); регенератор (3); холодный теплообменник (4); пульсационную трубку (5); горячий теплообменник (6); дроссель (7); инерционную трубку (8); резонатор (9); линию заправки и вакууми -рования, систему безопасности, систему зам ера, контр оля и регистрации параметров которые не изображены на рис.9.

Принципиальная схема эксперимент альной установки пульсационного охладителя и ее контрольно-измерительная система представлена на рис. 8. Генератор волн соединен с генератором сигналов (ВК Precision 4011A) и усилителем (CrownCE 1000). Генератор сигналов может создавать ^± 5,0 В гармонических колебаний с частотой 5,0 МГц. Верхний предел частоты колебаний генератора волн для КПО в данном исследовании 100 Гц. Для измерения напряжения (параллельно) и силы тока (последовательно) от генератора волн между генератором сигналов и генератором волн

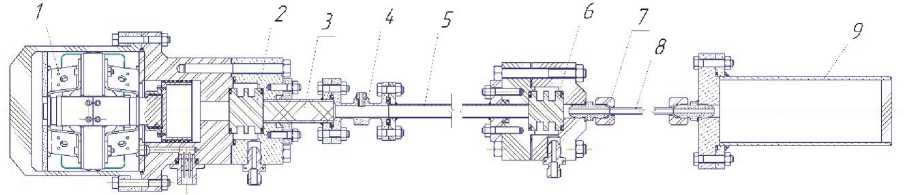
Рис. 7. Схема криогенного пульсационного охл адителя

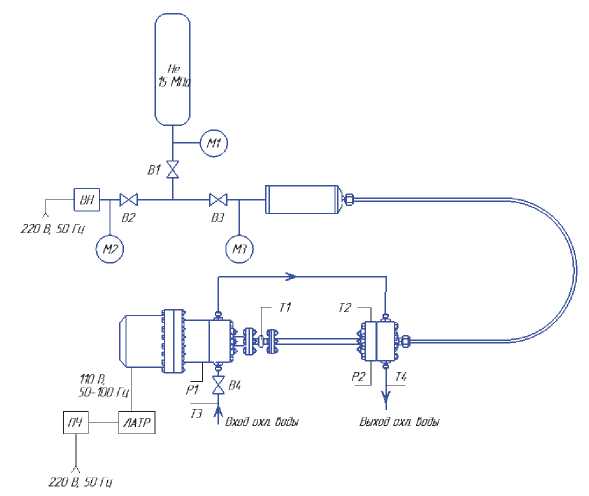
Рис. 8. Принципиальная схема экспериментальной установки пульсационного охладителя :

В1 – вентиль редуктора; В2 – вентиль насоса; В3 – вентиль заправки; В4 – вентиль охлаждающей среды; М1 – манометр давления в баллоне; М2 – манометр; М3 – манометр давления в КПО; ПЧ – преобразователь частоты; ЛАТР – лабораторный автотрансформатор; ВН – вакуумный насос; Т1 – датчик температуры холодного теплообменника; Т2 – датчик температуры горячего теплообменника; Т3 – датчик температуры охлаждающей среды; Т4– датчик температуры охлаждающей среды на выходе из КПО; Р1 – датчик давления («ОВЕН ПД 100»); Р2 – датчик давления («ОВЕН ПД 100»)

установлены два мультиметра. Эти измерения используются для расчетов полной входной мощности генератора волн.

Датчик давления «Омега» (РХ-309-500G5V) расположен с краю после генератора давлений. Термопара «Омега» типа К (незаземленный тип датчика) используется для измерения температуры газа в холодном теплообменнике с помощью компрессионного фитинга для предотвращения утечек из-за высокого давления в системе. Точность термопары примерно ± 1 К на уровне ниже 273 К.

Два тепл ообменника (т.е. предохладитель и холодный теплообменник) заключены в водоохлаждаемые кожухи. Регенератор, холодный теплообменник и часть пульсационной трубы заключены в вакуумные камеры. Вакуумные камеры используются для снижения потерь вследствие конвективного теплообмена КПО с окружающей средой. Давление в вакуумной камере достигает 20-30 мм рт. ст. Наличие влаж-ности/водяного пара приводит к образованию на-леди/льда в холодной части КПО. Для прочистки/ продувки вакуумн ой кам еры от водяного пара перед экспериментом через вакуумную камеру пропускается азот N₂ . Для уменьшения лучистого теплообмена компоненты охладителя были обернуты в отражающую фольгу.

По результатам числен ного моделирования оптимальным пр инимается режим с давлением заправки 2,2 МПа и частотой 65 Гц, которы й был выбран для первоначального эксперимента. В нач але исследований был проведен эксперимент при таких давлении и частоте. Эксперимент проводился в течение 30 минут времени работы пульсационного охладителя. Динамика изменения температуры в холодном теплообменнике термоакустического охладителя в течении хода эксперимента (30 минут) представлена на рис. 9. Минимальная полученная температура за это время была получена равной 242 К. Выравнивание температуры на данном уровне обусловлено установкой термодинамического равновесия из-за теплопритоков из внеш ней среды.

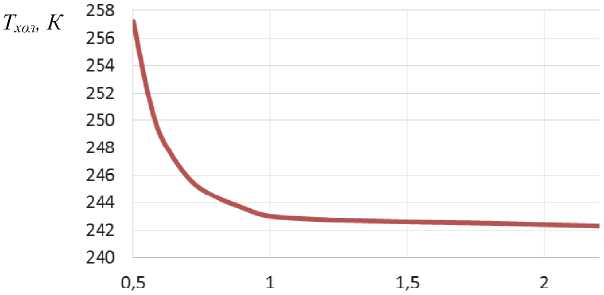
Далее для проверки различных режимов работу установки были проведены запуски при частоте колебаний 65 Гц и давлениях от 0,5 до 2,2 МПа. Как видно из графика (рис. 10) при увеличе- нии давления более 1 МПа уровень температуры на теплообменнике нагрузки постоянным. На основании предварительных испытаний сделан вывод о недостаточном уровне подводимой мощности данного типа линейного пульсатора для достижения необходимого уровня амплитуды давления при уровне давления заправки выше 1 МПа и частоте более 65 Гц. Таким образом, дальнейш ее снижение температуры для данной конструкции можно получить за счёт увеличения подводимой мощности. Кроме того, установка дополнительной изоляции с помощью вакуумной камер ы для зон холодного теплообменника нагрузки, регенератора и пульсационной трубы позволит устранить теплопритоки из окружающей среды и добиться пр оектного уровня температуры охлаждения.

Допустимые отклонения расчетных значений температуры охлаждения, полученных с помощью предпроектной методики оценки, от экспериментальныхсоставили 5-8%, что вполне допустимо для предварительной оценки уровня охлаждения и количества тепла, которое можно отвести в теплообменнике нагрузки. Применение данного способа расчета позволяет предварительно оценить соотношение объемов рабочих контуров пульсационной трубы и ресивера на требуемыйуровень температуры охлаждения для дальнейшего более точного расчета конструктивных размеров с помощью программы DeltaEC. Данный программ ный пр одукт позволяет моделировать акустические поля, процессы тепло- и массопереноса в каналах, а также рассчитывать эффективность термоакустических преобразователей. Однако в практическом плане он является крайне неудобным из-за трудностей, связ анных с плохой сходимостью и устойчивостью используемого в нем метода «стрельбы». В связи с этим разработанная предпроектная методика является простым и удобным способом расчёта термоакустических преобразователей, который позволяетоценить основные физико-технические и геометрические парам етры охладителя. Сравнительный анализ результатов моделирования пульсационного охладителя на основе двух конечно-элементных моделей показал близ кие значения температуры охлаждения и геометри-

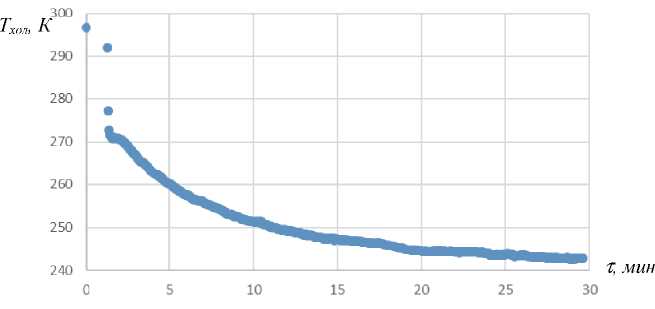
Рис. 9. Изменение миним альной температуры на хол одном теплообменнике в КПО при частоте 65 Гц и при давлении 2,2 МПа (толщина линии графика обусловлена пилообразным характером зависимости регистрируемых данных)

р, МПа

Рис. 10. И зменение минимальной температуры на холодном теплообменнике от давления в термоакустическом охладителе при частоте 65 Гц

ческих соотношений охладителя. Отклонения расчетны х результато в, полученных по разработанным методикам проектирования охладителя, от экспериментальных значений [9] находятся на допустимом уровне. Это позволяет сделать вывод о том, что при проектировании вновь создаваемой конструкции криогенного пульсационного охладителябудет рационально использовать приведенные разработанные модели расчета как последовательные этапы проектировочного расчета. Такой комплексный поэтапный подход инженерного расчета конструктивных парам ет ров пульсационного охладителя проектированию позволяет более обоснованно и рационально использовать методики проектирования в процессе создания термоакустических преобразователей.